|
|
|
发布时间: 2022-08-25 |
清洁安全发电 |
|
|
|
收稿日期: 2021-11-08
基金项目: 山西省科技重大专项(20181102010)
中图法分类号: TK227
文献标识码: A
文章编号: 2096-8299(2022)04-0341-06
|
摘要
湿法脱硫燃煤电厂烟气中含有大量的水蒸气, 形成具有视觉污染的白色烟羽。在脱硫塔后加装烟气冷凝器, 可以消除白色烟羽、回收大量水资源, 同时还可以进一步降低烟气中的污染物含量。针对Colburn-Hougen方法传质方程中j因子需要通过查表来获得的繁琐性, 基于菲克定律和传热传质类比定律, 推导出了一个传质系数Kv。利用获得的Kv, 采取逐段计算的方法设计了烟气冷凝器, 并进行了实验验证。结果表明: 设计计算结果与实验结果非常接近, 可以采用Kv计算水蒸气的冷凝速率, 采用逐段计算方法设计烟气冷凝器。
关键词
燃煤电厂; 湿法脱硫; 白色烟羽; 烟气冷凝器; Colburn-Hougen方法
Abstract
The flue gas of wet desulfurization coal-fired power plant contains a large amount of water vapor, which forms a white smoke plume with visual pollution.Installing a flue gas condenser after the desulfurization tower can eliminate white smoke plumes, recover a large amount of water resources, and further reduce the content of pollutants in the flue gas.In view of the cumbersomeness of the factor j in the mass transfer equation of the Colburn-Hougen method that needs to be obtained by looking up the table, based on Fick's law and the heat and mass transfer analogy law, a mass transfer coefficient Kv is derived.Using the obtained Kv, the flue gas condenser was designed by the section by section calculation method, and the experimental verification was carried out.The results showed that the design calculation results are very close to the experimental results.The Kv can be used to calculate the condensation rate of water vapor and the section by section calculation method can be used to design flue gas condenser.
Key words
coal-fired powr plant; wet desulfurization; white smoke plume; flue gas condenser; Colburn-Hougen method
我国90%以上的燃煤机组采用湿法脱硫, 年烟气量约24万亿m3, 其中约含水蒸气21亿t。大量的水蒸气伴随着烟气排放到空气中, 造成了水资源的浪费, 同时也带来了严重的视觉污染[1]。在脱硫塔后加装烟气冷凝器, 可以回收烟气中的大部分水蒸气, 同时可以深度脱除烟气中的硫酸雾、可溶性盐、细颗粒物等污染物[2], 对于缓解水资源匮乏及改善环境质量具有重要意义。
国内外学者对烟气冷凝器进行了大量的研究, 研究内容包括增强烟气冷凝器的防腐性能、开发防腐疏水的新材料以及强化换热等[3-4]。研究方法主要以实验和理论分析为主[5-6], 数值模拟也发挥着越来越重要的作用[7-8]。然而, 大部分研究都是针对已有的换热器, 鲜有关于烟气冷凝器设计方法的研究与验证。
烟气冷凝具有以下特点: 第一, 烟气冷凝是传热和传质同时进行的复杂过程, 随着烟气中水蒸气的冷凝和烟气温度的降低, 烟气的组成、物性以及流速均会发生变化; 第二, 烟气冷凝是显热和潜热同时发生的换热过程, 对流换热系数和烟气露点沿流程呈非线性变化; 第三, 由于烟气侧复杂的流动以及换热过程, 冷却水侧的温升速率并不是恒定的, 因此对数平均温差法和ε-NTU方法不适用于烟气冷凝器的设计。
烟气冷凝从组分上说属于含有大量不凝结气体的冷凝, 水蒸气作为可凝物占烟气组成的10%~15%, 而二氧化碳、氮氧化合物以及其他碳氢化合物等占烟气的绝大部分, 且均为不凝结成分。对于含大量不凝结气体蒸汽的冷凝, Colburn-Hougen提出的双膜理论[9]应用最为广泛。采用该理论计算冷凝器的换热面积相对准确, 但计算过程繁琐, 且传质方程中的j因子需要通过查表来获得。
本文利用菲克定律对烟气冷凝过程中的传质过程进行了分析, 并根据传热传质类比定律推导出了传质系数Kv, 获得了Colburn-Hougen方法中的热平衡方程式, 避免了在计算传质方程时通过查表来获得j因子等繁琐工作, 提高了计算结果的可靠性。
1 设计计算基础
1.1 烟气冷凝过程机理分析
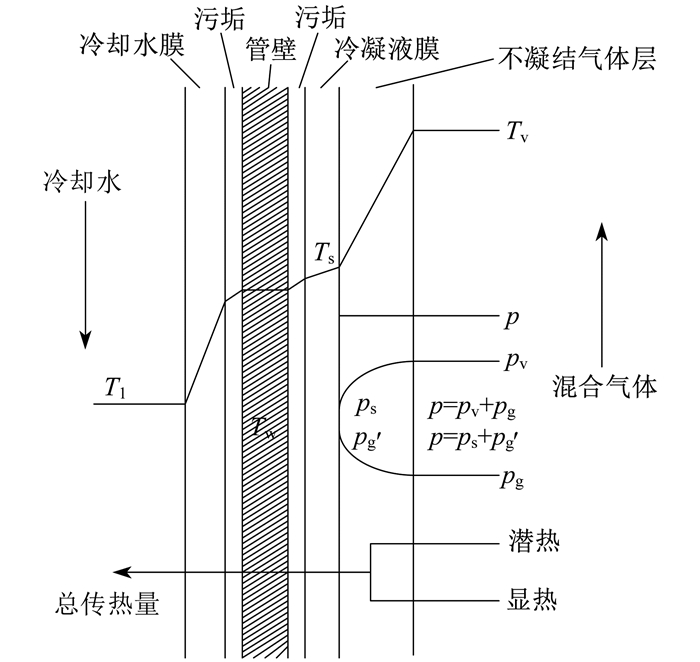
烟气在壁面冷凝时的传热机理如图 1所示。其中, T1为冷却水的温度, TW为壁面温度, Ts为壁面上冷凝液膜的温度, Tv为烟气主流的温度, p为二元混合物的总压, ps为冷凝液膜表面温度对应的水蒸气分压, pg为烟气中不凝结气体分压, p′g为冷凝液膜表面温度对应的不凝结气体分压, pv为水蒸气分压。
当壁面温度低于烟气的露点时, 烟气中的水蒸气冷凝, 水蒸气分压降低, 在壁面上形成一层冷凝液膜。烟气中不发生冷凝的组分在冷凝液膜表面生成一层不凝结气体层, 主流烟气中未冷凝的水蒸气需要穿过这层不凝结气体层才能在冷凝液膜上发生冷凝。烟气在壁面降温的同时伴随着水蒸气的冷凝, 这个过程同时进行着显热与潜热的交换, 并通过壁面传递至冷却水侧。从热平衡的角度来看, 烟气向冷凝液膜传递的显热与潜热之和等于冷凝液膜通过壁面向冷却水传递的热量。因此, 求解换热量的关键是确定冷凝液膜的表面温度。烟气的显热采用传热关联式计算, 潜热则通过传质方程求得水蒸气的冷凝量来计算。
1.2 分析和计算中的假设
为了便于后续分析和计算, 对实际烟气的冷凝过程作出以下假设: 烟气只在壁面上发生冷凝, 即不考虑烟气的空间冷凝; 烟气冷凝过程中的压力保持不变, 且一直处于饱和状态; 不考虑冷凝液滴对换热的影响; 将烟气视为水蒸气与干空气组成的二元混合气体。
1.3 传质系数的推导
由菲克定律可知, 由2种组分(A和B)组成的二元混合物在扩散且伴有混合物的主体流动时, 组分A通过某一界面的扩散通量为
| $ N_{\mathrm{A}}=-D \frac{\mathrm{d} C_{\mathrm{A}}}{\mathrm{d} z}+x_{\mathrm{A}}\left(N_{\mathrm{A}}+N_{\mathrm{B}}\right) $ | (1) |
式中: NA, NB——组分A和B的摩尔通量, kmol/(m2·s);
D——组分的扩散系数, m2/s;
CA——组分A的物质的量浓度, kmol/m3;
dCA/dz——组分A在扩散方向上的浓度梯度;
xA——组分A的摩尔分数。
由式(1)可知, 当组分在扩散且伴有混合物的主体流动时, 组分的实际传质通量除了包括分子扩散通量, 还应考虑主体流动对传质的影响。
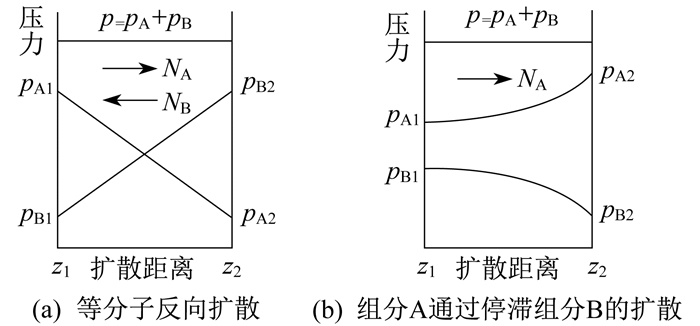
二元混合物在扩散过程有双向扩散和单向扩散2种形式。当把二元混合物的扩散过程视为等分子反向扩散时, 组分A向组分B扩散, 同时组分B也向组分A扩散。扩散形式如图 2所示。其中: pA和pB分别为组分A和组分B的分压; pA1和pA2为组分A在z1和z2处的分压; pB1和pB2为组分B在z1和z2处的分压。
对于式(1) 有NA=-NB, 由此可得
| $ N_{\mathrm{A}}=-D \frac{\mathrm{d} C_{\mathrm{A}}}{\mathrm{d} z} $ | (2) |
对于压力不高的扩散过程, 二元混合物可视为理想气体混合物, 则二元混合物的物质的量浓度C=p/RT。式中, R为通用气体常数, T为热力学温度。
将式(2)分离变量并积分, 可得
| $ N_{\mathrm{A}}=\frac{D}{R T \Delta z}\left(p_{\mathrm{A} 1}-p_{\mathrm{A} 2}\right) $ | (3) |
式中: Δz——组分A的扩散距离, m。
当把二元混合物的扩散过程视为单向扩散时, 即组分B视为停滞组分, 只发生组分A穿过组分B的扩散, 则式(1)中NB=0, 由此可得
| $ N_{\mathrm{A}}=-D \frac{\mathrm{d} C_{\mathrm{A}}}{\mathrm{d} z}+x_{\mathrm{A}} N_{\mathrm{A}}=-\frac{D C}{C-C_{\mathrm{A}}} \frac{\mathrm{d} C_{\mathrm{A}}}{\mathrm{d} z} $ | (4) |
对式(4)分离变量并积分, 可得
| $ N_{\mathrm{A}}=\frac{D p}{R T \Delta z} \ln \frac{p-p_{\mathrm{A} 2}}{p-p_{\mathrm{A} 1}} $ | (5) |
假设扩散过程中总压保持不变, 即p=pA1+pB1=pA2+pB2, 则式(5)可变换为
| $ N_{\mathrm{A}}=\frac{D p}{R T \Delta z} \times \frac{p_{\mathrm{A} 1}-p_{\mathrm{A} 2}}{p_{\mathrm{B} 2}-p_{\mathrm{B} 1}} \ln \frac{p_{\mathrm{B} 2}}{p_{\mathrm{B} 1}} $ | (6) |
令pcf=(pB2-pB1)/ln(pB2/pB1), pcf为组分B的对数平均分压[10], 则
| $ N_{\mathrm{A}}=\frac{D p}{R T \Delta z} \times \frac{p_{\mathrm{A} 1}-p_{\mathrm{A} 2}}{p_{\mathrm{cf}}} $ | (7) |
由于p为二元混合物的总压, 故可将式(7)中等号右边的第一部分视为二元混合物向壁面单向扩散时的扩散通量Ng, 而二元混合物向壁面的扩散通量即为混合物与壁面之间的对流传质速率, 由此可得
| $N_{\mathrm{g}}=\frac{D p}{R T \Delta z}=\frac{D C}{\Delta z}=h_{\mathrm{m}}\left(C_{\infty}-C_{\mathrm{g}}\right) $ | (8) |
式中: hm——对流传质系数, m/s;
C∞——二元混合物的主流浓度, kmol/m3;
Cg——二元混合物在壁面的浓度, kmol/m3, 取Cg=0。
根据传热传质类比定律和刘易斯关系式, 可得出
| $ h_{\mathrm{m}}=\frac{h}{C_{\mathrm{p}} \rho}\left(\frac{D}{a}\right)^{\frac{2}{3}} $ | (9) |
式中: h——对流换热系数, W/(m2·K);
Cp——混合物的定压比热容, kJ/(kg·K);
ρ——混合物的密度, kg/m3;
a——混合物的导温系数, m2/s。
将式(9)及C=ρ/M代入式(8)中, 可得
| $ N_{\mathrm{g}}=\frac{h}{C_{\mathrm{p}} M}\left(\frac{D}{a}\right)^{\frac{2}{3}} $ | (10) |
式中: M——二元混合物的摩尔质量, g/mol。
令Kv=Ng, 将其定义为烟气冷凝过程中水蒸气的传质系数, 单位为mol/(m2·s), 则水蒸气的扩散通量可表示为
| $N_{\mathrm{A}}=K_{\mathrm{v}} \times \frac{p_{\mathrm{A} 1}-p_{\mathrm{A} 2}}{p_{\mathrm{cf}}}=K_{\mathrm{v}} \times \ln \frac{p_{\mathrm{B} 2}}{p_{\mathrm{B} 1}} $ | (11) |
进而得出水蒸气的冷凝量为mA=NAMv, 其中Mv为水的摩尔质量。
1.4 扩散系数的求解
不同物质之间的扩散系数一般由实验测定。对于二元组分混合物扩散系数的理论计算主要有以下2种方法。
一是实验测定某一温度压力下组分A在组分B中的扩散系数, 然后通过式(12)求出其他情况下的扩散系数。该方法需要实验测定参考工况下的扩散系数。
| $ D=D_0 \frac{p_0}{p}\left(\frac{T}{T_0}\right)^{\frac{3}{2}} $ | (12) |
式中: D0, p0, T0——参考工况下的扩散系数、压力和温度。
二是用吉利兰提出的半经验公式(13)来计算。
| $ D=\frac{435.7 T^{\frac{3}{2}}}{p\left(V_{\mathrm{A}}^{\frac{1}{3}}+V_{\mathrm{B}}^{\frac{1}{3}}\right)^2} \sqrt{\frac{1}{M_{\mathrm{A}}}+\frac{1}{M_{\mathrm{B}}}} $ | (13) |
式中: VA, VB——组分A和B在正常沸点时的液态摩尔容积, cm3/mol;
MA, MB——组分A和B的分子量。
1.5 换热量及热平衡方程
根据烟气冷凝过程的传热机理, 烟气冷凝同时进行着显热和潜热的传递, 对微元换热面dA的传热过程进行分析。
烟气侧的显热量dQcool采用传热关联式进行计算, 公式为
| $d_{\mathrm{Q}_{\text {cool }}}=h_{\mathrm{g}}\left(T_{\mathrm{g}}-T_{\mathrm{s}}\right) d_{\mathrm{A}} $ | (14) |
式中: hg——烟气与冷凝液膜间的对流换热系数, W/(m2·K);
Tg——烟气的主流温度, K。
烟气冷凝过程中的潜热量是根据水蒸气冷凝量来计算, 而水蒸气的冷凝量是通过计算水蒸气向冷凝壁面的扩散通量得到, 故烟气冷凝过程中的潜热量dQcond为
| $d_{\mathrm{Q}_{\mathrm{cond}}}=K_{\mathrm{v}} M_{\mathrm{v}} r \ln \frac{p_{\mathrm{g}}^{\prime}}{p_{\mathrm{g}}} \times 10^{-3} d_{\mathrm{A}} $ | (15) |
式中: r——水的潜热, kJ/ kg。
烟气向冷凝液膜传递的热量(潜热与显热之和)为
| $ d_{\mathrm{Q}_1}=d_{\mathrm{Q}_{\text {cool }}}+d_{\mathrm{Q}_{\text {cond }}}=h_{\mathrm{g}}\left(T_{\mathrm{g}}-T_{\mathrm{s}}\right) d_{\mathrm{A}}+\\ K_{\mathrm{v}} M_{\mathrm{v}} r \ln \frac{p_{\mathrm{g}}^{\prime}}{p_{\mathrm{g}}} \times 10^{-3} d_{\mathrm{A}} $ | (16) |
冷凝液膜向冷却水传递的热量(显热)为
| $ d_{\mathrm{Q}_2}=h_{\mathrm{e}}\left(T_{\mathrm{s}}-T_1\right) d_{\mathrm{A}} $ | (17) |
式中: he——冷凝液膜到冷却水的复合传热系数, W/(m2·K)。
根据热平衡原理, 烟气向冷凝液膜传递的热量与冷凝液膜向冷却水传递的热量相等, 即
| $\begin{gathered} h_{\mathrm{g}}\left(T_{\mathrm{g}}-T_{\mathrm{s}}\right) d_{\mathrm{A}}+K_{\mathrm{v}} M_{\mathrm{v}} r \ln \frac{p_{\mathrm{g}}^{\prime}}{p_{\mathrm{g}}} \times 10^{-3} d_{\mathrm{A}}= \\ h_{\mathrm{e}}\left(T_{\mathrm{s}}-T_1\right) d_{\mathrm{A}} \end{gathered} $ | (18) |
1.6 计算方法
由于烟气冷凝过程的复杂性和特殊性, 根据Colburn-Hougen提出的双膜理论, 本文采用分段分区试凑法来计算换热面积, 即温度分段、面积分区、膜温试凑。分段分区的逐段计算方法类似于数学中的积分思想, 根据设计参数将冷凝器分成适当的温度区间, 每个区间内的烟气物性及换热参数视为定值, 然后分别计算各个区间所需的换热面积。
在各个区间端点利用式(18)进行热平衡计算时, 只有液膜表面的温度Ts是未知的, 需要通过试凑法求得。
分段分区试凑法的计算过程如下。
(1) 假定换热面积, 确定冷凝器的概略尺寸。
(2) 根据设计参数, 将冷凝器分成适当的温度区间。
(3) 计算区间端点烟气的物性以及式(14)~式(16)中的相关参数。
(4) 采用试凑法, 根据式(17)计算冷凝液膜的表面温度Ts。
(5) 计算区间端点的K(Tg-Tw)值及其对数平均值, K为烟气主流到冷却水侧的对流换热系数, 单位为W/(m2·K)。
(6) 根据区间端点的烟气状态, 计算各个区间的换热量ΔQ。
(7) ΔQ除以K(Tg-Tw)的对数平均值即为各个区间的换热面积。
(8) 各个区间的换热面积相加, 且考虑温差修正系数后即为冷凝器总的换热面积。若其与假定换热面积的误差在10%~15%, 则认为其是合理的。
2 冷凝器的设计计算
燃煤电厂采用湿法脱硫时, 脱硫塔出口烟气处于饱和或过饱和状态, 烟温在55~60 ℃。因此, 设计计算时烟气冷凝器进口烟温为55 ℃, 出口烟温为25 ℃, 冷却水进口温度为15 ℃, 与烟气逆流布置, 将冷凝器划分为6个区间进行计算。烟气在冷凝器中与冷却水换热时, 物性变化较大。物性计算在烟气冷凝器设计计算中尤为重要。将烟气视为水蒸气与干空气的混合物, 导热系数、黏度等物性计算采用湿空气热物性计算方程[11], 主要计算结果如表 1所示。本文设计计算的换热面积为2.23 m2, 考虑换热裕量及其他因素, 冷凝器实际加工时的换热面积为2.32 m2。
表 1
冷凝器设计计算主要结果
| 烟气侧区间端点温度/℃ | 烟气体积流量/(m3·h-1) | 区间冷凝水量/(kg·h-1) | 区间换热量/W | 区间端点冷却水温度/℃ | 各区间面积/m2 |
| 55 | 90.00 | 25.00 | |||
| 50 | 85.23 | 2.30 | 2 041.15 | 21.99 | 0.288 |
| 45 | 81.39 | 1.74 | 1 506.98 | 19.77 | 0.268 |
| 40 | 78.23 | 1.32 | 1 137.88 | 18.09 | 0.264 |
| 35 | 75.57 | 1.00 | 874.62 | 16.80 | 0.275 |
| 30 | 73.29 | 0.77 | 682.50 | 15.79 | 0.303 |
| 25 | 71.29 | 0.58 | 538.66 | 15.00 | 0.364 |
| 20 | 69.51 | 0.44 | 418.46 | 15.00 | 0.555 |
3 实验设计和结果
3.1 实验系统
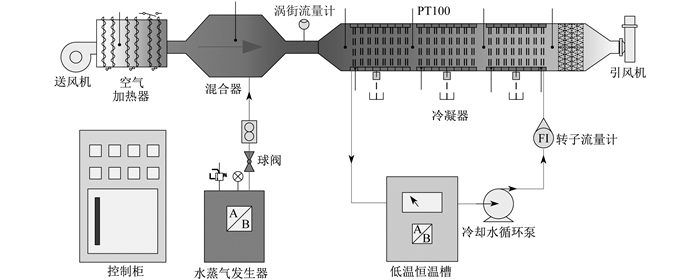
根据设计计算结果, 考虑换热裕量以及制作的便利性, 将冷凝器设计为管箱结构, 实验系统如图 3所示。采用外径14 mm、壁厚1 mm、长度200 mm的光管, 正三角形叉排布置, 烟气横向冲刷管束, 11根光管为1组, 共24组264根光管。
空气被加热器加热后, 在混合器中与水蒸气发生器产生的水蒸气混合, 形成的饱和或近饱和湿空气在冷凝器中被冷却水冷却, 冷凝水从冷凝器下部由水封装置排出。冷却水在冷凝器中与湿空气换热后, 由低温恒温槽降温, 经循环泵送入冷凝器继续与湿空气换热。烟气侧和冷却水侧各均匀布置4个PT100温度测点, 进口分别安装涡街流量计和转子流量计测量烟气和冷却水流量。系统电源以及仪表显示均由控制柜控制。
3.2 实验条件
实验工况与设计计算工况相同。通过调整送风机和引风机频率、空气加热器温度及水蒸气发生器的功率和阀门开度, 使冷凝器进口湿空气流量为90 m3/h, 温度为55 ℃。调整冷却水循环泵功率和低温恒温槽温度, 使冷却水进口流量为583 L/h, 温度为15 ℃。为了保证实验的可靠性, 实验进行了2次以上。
3.3 结果与分析
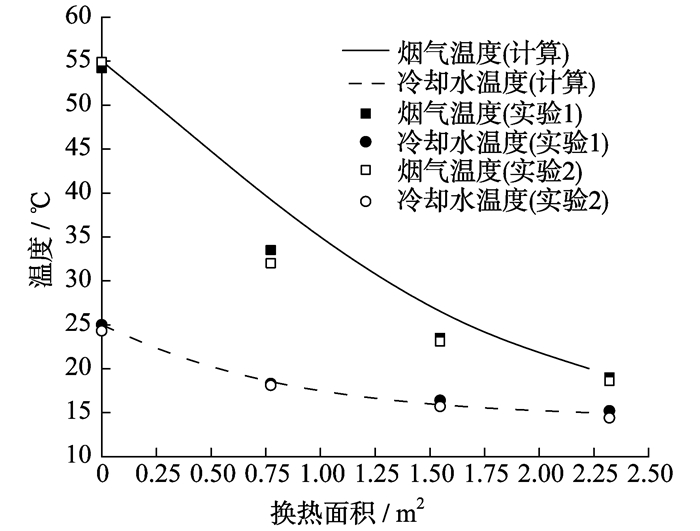
实验中, 调整烟气和冷却水侧的进口参数与设计计算一致, 通过测量烟气和冷却水的出口温度以及冷凝水量来验证设计计算的正确性。设计计算冷凝水量为8.15 L/h, 实验中1 h收集的冷凝水量为7.9 L。实验中烟气和冷却水的温度变化如图 4所示。
由图 4可以看出, 对于相同的换热面积, 设计计算与实验结果十分接近, 说明了设计方法的可靠性; 实验得到的烟气出口温度比设计计算的理论值大约低3 K, 主要是因为设计计算过程中只考虑了烟气与管束的换热, 而制作冷凝器时采用了管箱结构, 支撑管束的隔板在隔绝烟气与冷却水的同时相当于增加了1个换热面, 烟气会通过隔板与冷却水换热。这也是实验收集的冷凝水量比设计计算多的原因之一。
由图 4还可以看出, 烟气降温速率的设计计算与实验结果差别较大, 主要是因为设计计算时假设所有管束均为膜状冷凝, 且忽略了冷凝液滴对烟气流动和换热的影响, 而实验中冷凝器进口几排管束的烟气流速远大于设计计算流速, 换热效果较设计计算要强, 且冷凝液滴也会在一定程度上强化下排管束的换热效果。同时, 烟气在冷凝器中的降温速率是非线性的, 主要是因为随着烟气中水蒸气含量的降低, 换热面积相同时烟气的降温幅度减小, 也可理解为随着水蒸气含量的降低, 对烟气换热的强化效果减弱。此外, 烟气的物性变化以及流速降低也会影响烟气的降温速率。然而, 烟气侧温度的非线性变化造成了冷却水侧温度的非线性变化, 这也是对数平均温差法和ε-NTU方法无法用于烟气冷凝器设计的主要原因。
4 结论
(1) 使用传质系数Kv计算烟气冷凝过程中, 将水蒸气的冷凝速率用于烟气冷凝器的设计, 实验结果与设计计算结果十分接近, 说明了将Kv和逐段计算方法用于烟气冷凝器设计的可靠性。
(2) 当水蒸气含量较高, 采用逐段计算方法时, 温度区间的划分范围应尽可能小, 以提高计算的准确性。
(3) 冷凝液滴会在一定程度上强化烟气冷凝换热。
(4) 随着水蒸气的冷凝, 烟气冷凝换热系数减小, 强化烟气冷凝换热时应着重关注烟气冷凝器后半段的强化效果。
参考文献
-
[1]刘志坦, 惠润堂, 杨爱勇, 等. 燃煤电厂湿烟羽成因及对策研究[J]. 环境与发展, 2017, 29(10): 43-46.
-
[2]吴晓蔚, 刘启贞, 沈志刚. 燃煤电厂石膏雨污染排放实测[J]. 环境监测管理与技术, 2017, 29(3): 41-44.
-
[3]朱峰, 王随林, 刘贵昌, 等. 新型防腐表面烟气冷凝换热器换热研究[J]. 建筑科学, 2019, 35(2): 147-154.
-
[4]苗瑞环. 耐腐蚀烟气冷凝换热器换热性能研究[D]. 北京: 北京建筑大学, 2013.
-
[5]熊英莹, 谭厚章, 许伟刚, 等. 火电厂烟气潜热和凝结水回收的试验研究[J]. 热力发电, 2015, 44(6): 77-81.
-
[6]SHI X J, CHE D F, AGNEW B, et al. An investigation of the performance of compact heat exchanger for latent heat recovery from exhaust flue gases[J]. International Journal of Heat and Mass Transfer, 2011, 54: 606-615. DOI:10.1016/j.ijheatmasstransfer.2010.09.009
-
[7]MACHÁCKOVÁ A, KOCICH R, BOJKO M, et al. Numerical and experimental investigation of flue gases heat recovery via condensing heat exchanger[J]. International Journal of Heat and Mass Transfer, 2018, 124: 1321-1333.
-
[8]LI J D. CFD simulation of water vapor condensation in the presence of non-condensable gas in vertical cylindrical condensers[J]. International Journal of Heat and Mass Transfer, 2013, 57: 708-721.
-
[9]COLBURN A P, HOUGEN O A. Design of cooler condensers for mixtures of vapors with noncondensing gases[J]. Industrial and Engineering Chemistry, 1934, 26(11): 1178-1182.
-
[10]连之伟, 陈宝明. 热质交换原理与设备[M]. 北京: 中国建筑工业出版社, 2018: 25.
-
[11]纪威, 杨萱. 湿空气热物理性质计算方程[J]. 暖通空调, 1996(3): 16-19.