|
|
|
发布时间: 2022-08-25 |
智能制造与新材料 |
|
|
|
收稿日期: 2022-03-26
中图法分类号: TK124
文献标识码: A
文章编号: 2096-8299(2022)04-0396-07
|
摘要
使用有限元方法对电路板的冷却进行了数值模拟, 分析了印制电路板上的元器件布局在强迫对流下的冷却效果, 其中主要包括元器件的并排、叉排以及元器件间的纵向和横向间距, 得到了该模型下的温度场和速度场。引入信息熵等评价性指标对温度场和速度场进行了量化分析, 可以发现: 元器件并排的冷却效果优于叉排; 较大功率的芯片距离冷却气体入口处越近越好; 在元器件之间的纵向间距尽可能大的同时选择一个合适的横向间距。
关键词
印制电路板; 元器件布局; 温度场; 速度场; 信息熵
Abstract
Based on the finite element method, the cooling of the printed circuit board is numerically simulated, and the cooling effect of the component layout on the circuit board under forced convection is analyzed, including the side-by-side and cross rows of components and the vertical and horizontal spacing between components. The temperature field and velocity field under the model are obtained. Shannon entropy and other evaluation indexes are introduced to quantitatively analyze the temperature field and velocity field. It is found that the cooling effect of side-by-side components is better than that of cross rows, and the closer the high-power chip is to the inlet of cooling gas, the better. The longitudinal spacing between components is as large as possible, and an appropriate transverse spacing is selected at the same time.
Key words
printed circuit board; component layout; temperature field; velocity field; Shannon entropy
印制电路板(以下简称“电路板”), 是电子产品中必不可少的部件, 从计算器、电子手表等小型电子设备到计算机、军用武器系统等大型电子设备, 都需要使用电路板将电子元器件进行电气互连[1]。当组件和元器件内部积聚过多热量时, 就会导致电路板温升过高, 严重影响了电子元器件的性能。相关数据表明, 过高的热环境应力使得55%的电子产品失效[2], 同时元器件的P-N结结温每升高10 K, 其失效率将增加1倍以上, 即10 K法则[3]。因此, 避免发热电子元器件所产生的热量积聚, 有效排出热量, 防止出现热失效问题, 是电子设备热分析中一个至关重要的环节。
文献[4]针对功率型电路板建立了强迫对流三维模型, 采用有限元方法, 得到了电路板在强制对流条件下的温度分布图和速度分布图, 以及电路板表面最高温度和表面最大流速随不同功率密度变化的关系。文献[5]运用有限元软件COMSOL中的非等温模块对长方体机箱中电子元件散热情况进行了数值分析, 通过耦合层流和传热模块进行仿真分析, 将电子元件作为恒定热源, 空气作为冷却介质, 仿真模拟了长方体机箱中的温度场和速度场, 分析了不同入口速度和不同材料的散热器对散热效果的影响。文献[6]提出了一种结合信息熵与改进K-means算法的异常检测算法, 结果表明: 改进算法具有更高的检测率和更低的误检率, 应用于电力负荷数据检测时检测率达到了90.5%, 能够有效地检测出异常的负荷数据。
本文使用有限元软件COMSOL, 对基于强迫对流下的电路板元器件布局及元器件间的纵向和横向间距进行简化建模计算, 并得到其温度场和速度场, 引入均值、标准差、平滑度、三阶矩、一致性、信息熵相关评价性指标对温度场和速度场进行量化分析。
1 模型构建
在连续介质力学范畴下, 纳维-斯托克斯方程是流体力学的基本方程[7]。它反映了真实流体流动的基本力学规律。连续性方程是质量守恒方程在流体中的表达式。流体的速度、压力等参数是由纳维-斯托克斯方程和连续性方程共同决定的, 而物体中的温度则是受能量方程所制约。
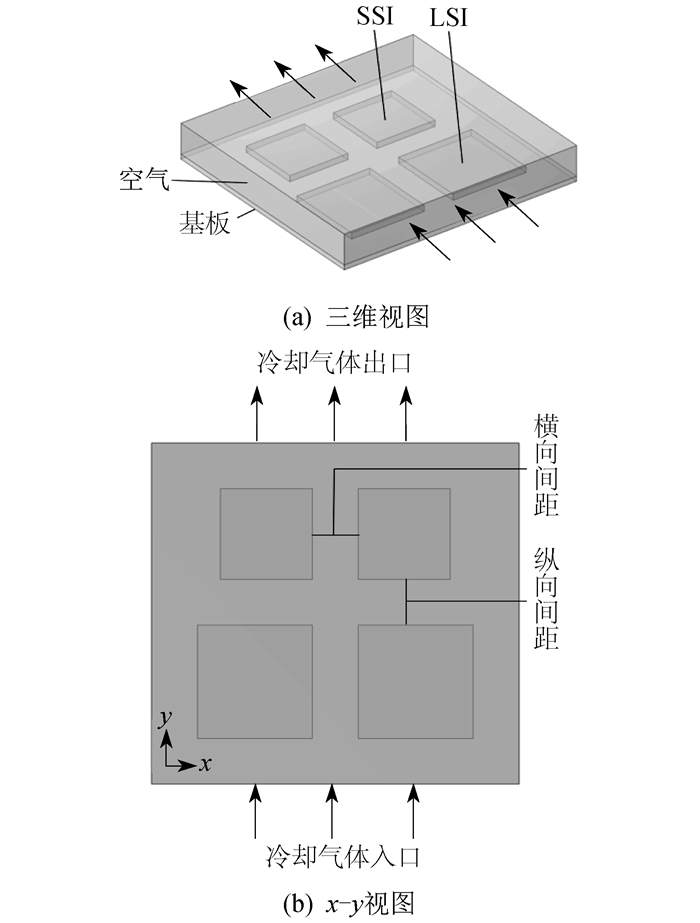
为了能够进行热分析, 有必要合理简化电路板的结构, 忽略板上外形结构和热量较小的片式电容和电阻。不同发热元器件的封装和材料性质也不相同, 需要对其结构进行简化。忽略外形结构规则的元器件引脚, 并用圆柱体或长方体代替[8]。模拟中, 计算模块电路板主要包括2个较大功率元器件(Large Scale Integrated, LSI), 型号为BSP75N, 2个较小功率元器件(Small Scale Integrated, SSI), 型号为LTM4601, 共4个发热元器件。电路板上各个组成部件的名称、尺寸、功率以及材料设置, 如表 1所示。
表 1
几何尺寸及材料设置
| 部件 | 长(x) | 宽(y) | 高(z) | 功率/W | 材料 | 导热系数/[W·(m·K)-1] |
| mm | ||||||
| 基板 | 80 | 75 | 1.6 | FR4 | 0.3 | |
| LSI | 25 | 25 | 2.0 | 2 | 硅 | 130.0 |
| SSI | 20 | 20 | 2.0 | 1 | 硅 | 130.0 |
| 冷却区域 | 80 | 75 | 10.0 | 空气 | ||
按照电路板部件的几何尺寸构建基本模型,如图 1所示。
该模型的基本参数设置具体如下: SSI热源输入为8.33×105 W/m3; LSI热源输入为1.07×106 W/m3; 空气温度为300 K; 空气压力为1.013 3×105 Pa; 空气入口速度为1 m/s。
利用COMSOL软件对多物理场耦合及稳态研究建立仿真, 在给定的外部空气温度条件下, 忽略电路板正面和背面的发热。为了模拟强迫制对流, 设置入口速度分布vy, 使其在x(水平)方向上是匀速, 在z(垂直)方向上呈抛物线状(空气的动力黏度受温度影响, 电路板上方空气的流动状态类似于充分发展的层流)。相关方程为
| vy=4vmax | (1) |
式中: vmax——空气入口速度;
hz——电路板上方空气域的高度, 为冷却区域高度的1/10。
在出口处, 模型使用抑制回流和零压力边界条件。此外, 在电路板和元器件表面应用无滑移条件, 对侧面设置周期性边界条件, 使同一水平方向上的两个边界温度都相等。最后, 模型中内部边界上的温度和热通量保持连续性。
2 评价指标的确定
本文采用的6种评价性指标分别为均值、标准差、平滑度、三阶矩、一致性、信息熵。令ai代表数据值的随机变量, 并令p(ai)为对应区域中数值的概率分布(i=0, 1, 2, …, L-1)。其中L为可区分的灰度级数[9]。那么关于ai的均值的第n阶矩μn(ai)为
| \mu_n\left(a_i\right)=\sum\limits_{i=0}^{L-1}\left(a_i-m\right)^n p\left(a_i\right) | (2) |
式中: m——ai的均值。
均值在电路板的温度场和速度场分布图描述中十分重要, 能够有效体现出温度场和速度场的平均值。均值m可表示为
| m=\sum\limits_{i=0}^{L-1} a_i p\left(a_i\right) | (3) |
标准差是电路板场分布图描述中的重要参数, 不仅可以表明样本偏离均值的程度, 还可以反映样本内部的波动程度。标准差能清晰地显示出电路板温度场和速度场的摆动幅度。标准差σ可表示为
| \sigma=\sqrt{\mu_2\left(a_i\right)}=\sqrt{\boldsymbol{\sigma}^2} | (4) |
式中: μ2(ai)——随机变量的二阶矩。
平滑度表示场分布图的平滑程度, 与标准差所衡量的对象在本质上是一致的。平滑度R可表示为
| R=1-\frac{1}{1+\boldsymbol{\sigma}^2} | (5) |
三阶矩表示电路板场分布图向左或向右偏斜的程度。如果均分布图是对称的, 则度量值为零; 如果向右偏斜, 即元器件上方, 则度量值为正值; 如果向左偏斜, 即元器件侧, 则度量值为负值。由式(2)得三阶矩μ3为
| \mu_3\left(a_i\right)=\sum\limits_{i=0}^{L-1}\left(a_i-m\right)^3 p\left(a_i\right) | (6) |
一致性是反映电路板场分布图均匀程度的参数。一致性U可表示为
| U=\sum\limits_{i=0}^{L-1} p^2\left(a_i\right) | (7) |
信息熵, 是1948年SHANNON C E提出的概念, 解决了信息的量化度量问题。信息熵是一种随机性度量, 也是电路板场分布图信息量的度量。当场分布图的值分布随机性越大时, 信息熵的值越大; 当场分布图的值不变的, 信息熵的值为零。信息熵e可表示为
| e=\sum\limits_{i=0}^{L-1} p\left(a_i\right) \lg \left(a_i\right) | (8) |
3 数值模拟结果与分析
3.1 5种电路板布局
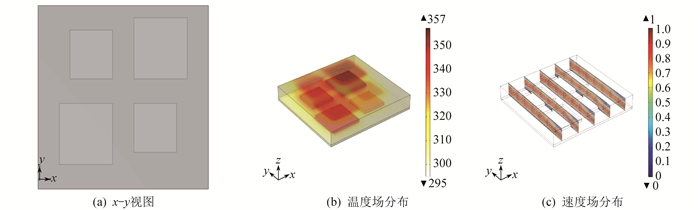
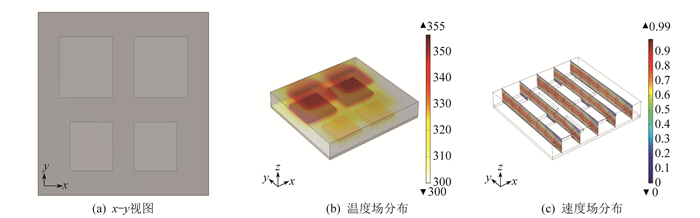
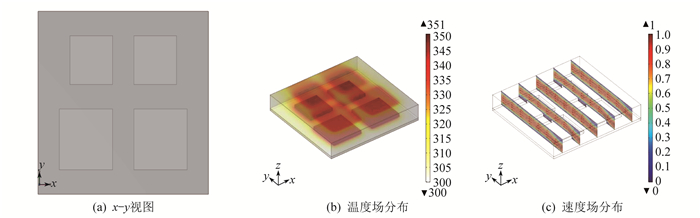
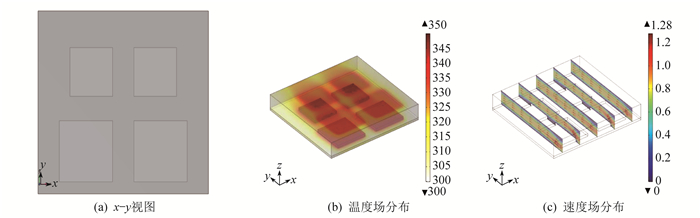
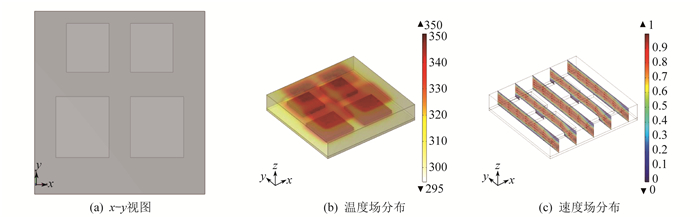
电路板元器件的5种不同布局下的x-y视图、温度场和速度场分布图如图 2至图 6所示。同时, 在速度分布图中引入流线标明强迫对流的流动方向。
布局1为LSI和SSI纵向间距10 mm, 横向间距10 mm, LSI与入口和出口距离分别为10 mm。
布局2为LSI和SSI纵向间距10 mm, 横向间距10 mm, SSI与入口距离10 mm, LSI与出口距离10 mm。
布局3为LSI和SSI纵向间距10 mm, 横向间距10 mm, LSI与入口距离10 mm, SSI与出口距离10 mm。
布局4为LSI和SSI纵向间距10 mm, 横向间距10 mm, LSI与入口距离5 mm, SSI与出口距离15 mm。
布局5为LSI和SSI纵向间距10 mm, 横向间距10 mm, LSI与入口距离15 mm, SSI与出口距离5 mm。
由图 2至图 6可以看出, 当LSI和SSI交叉排列时, 即布局1, 电路板的最高温度为357 K, 最大温升为57 K。当LSI和SSI并排且SSI位于入口处时, 即布局2, 电路板的最高温度为355 K, 最大温升为56 K, 且较多热量主要分布在LSI附近。其他3种布局下的最大温度均为350 K左右, 最大温升为50 K。值得注意的是, 布局4下的速度场最大值较其他布局大, 这是因为LSI离入口处较近, 加强了对冷却气体的扰动, 使得LSI所在的一端空气流动速度较快, 但整体速度场分布与其他布局差异不大。
根据不同布局下的温度场和速度场分布图, 计算出对应的信息熵等评价性指标分别如表 2和表 3所示。
表 2
不同布局下温度场的评价性指标
| 布局 | 均值/K | 标准差 | 平滑度 | 三阶矩 | 一致性/×10-5 | 信息熵 |
| 1 | 331.2 | 19.2 | 0.997 3 | -2 331 | 5.20 | 3.92 |
| 2 | 328.7 | 19.7 | 0.997 4 | -578 | 5.20 | 3.72 |
| 3 | 333.1 | 18.1 | 0.996 9 | -3 764 | 5.20 | 3.73 |
| 4 | 332.4 | 16.8 | 0.996 5 | -2 972 | 5.20 | 3.75 |
| 5 | 331.9 | 18.9 | 0.997 2 | -3 853 | 5.20 | 3.58 |
表 3
不同布局下速度场的评价性指标
| 布局 | 均值/(m·s-1) | 标准差 | 平滑度 | 三阶矩 | 一致性 | 信息熵 |
| 1 | 0.477 | 0.322 1 | 0.094 | 0.004 3 | 0.005 | 4.05 |
| 2 | 0.464 | 0.312 2 | 0.089 | 0.004 7 | 0.005 | 4.04 |
| 3 | 0.472 | 0.322 3 | 0.095 | 0.004 1 | 0.005 | 4.05 |
| 4 | 0.480 | 0.338 2 | 0.103 | 0.003 4 | 0.005 | 3.91 |
| 5 | 0.460 | 0.314 1 | 0.091 | 0.004 8 | 0.005 | 4.01 |
表 2中, 布局2的温度均值最低为328.7 K, 其他布局均在332 K左右; 布局4的标准差最小, 表示在该布局下, 电路板上各处的温度偏离平均温度的程度最小, 板上出现的热应力最小。5种布局下的平滑度相差无几, 由于平滑度和标准差相互呼应, 标准差的解释也同样适合平滑度。5种布局下温度场三阶矩的值均为负值, 说明热量主要分布在元件侧, 布局对温度分布的影响较小。5种布局下一致性的值相同, 说明在计算分析中各个布局下的取值很均匀。信息熵代表了温度场分布的随机性, 布局5的信息熵值最小, 即其温度场分布的随机性最小。
表 3中, 5种布局下的速度均值相差不大, 其中布局4的速度均值、标准差和平滑度最大, 即该布局下速度分布最不均匀, 但布局4的信息熵值最小, 即其速度分布的随机性最小。5种布局的速度场三阶矩值均为正值, 说明速度场主要分布在电路板上方, 因此上方元器件的冷却效果优于下方。5种布局下一致性的值均相同, 说明在计算分析中的取值很均匀。
3.2 间距对电路板冷却效果的影响
在布局3条件下, 改变LSI与SSI的纵向间距和横向间距, 并观察该因素对电路板冷却的影响。
3.2.1 不同纵向间距下的评价时指标
固定元器件间的横向间距, 纵向移动LSI的位置, 改变其与SSI的间距, 得到电路板的温度场和速度场分布图, 计算对应的信息熵等评价性指标, 结果如表 4和表 5所示。
表 4
不同纵向间距下温度场的最大温度及评价性指标
| 纵向间距/mm | 最大温度/K | 均值/K | 标准差 | 平滑度 | 三阶矩 | 一致性/×10-5 | 信息熵 |
| 10 | 351.1 | 333.1 | 18.1 | 0.996 9 | -3 761 | 5.20 | 3.744 |
| 11 | 350.6 | 332.9 | 17.7 | 0.996 8 | -3 554 | 5.20 | 3.733 |
| 12 | 350.1 | 332.7 | 17.4 | 0.996 7 | -3 365 | 5.20 | 3.669 |
| 13 | 349.8 | 332.6 | 17.2 | 0.996 6 | -3 212 | 5.20 | 3.659 |
| 14 | 349.1 | 332.3 | 16.8 | 0.996 5 | -2 995 | 5.20 | 3.658 |
| 15 | 348.5 | 331.9 | 16.5 | 0.996 3 | -2 796 | 5.20 | 3.647 |
表 5
不同纵向间距下速度场的评价性指标
| 纵向间距/mm | 均值/(m·s-1) | 标准差 | 平滑度 | 三阶矩 | 一致性 | 信息熵 |
| 10 | 0.471 | 0.322 | 0.094 | 0.004 0 | 0.005 | 4.05 |
| 11 | 0.472 | 0.324 | 0.095 | 0.003 3 | 0.005 | 4.02 |
| 12 | 0.474 | 0.327 | 0.097 | 0.003 3 | 0.005 | 4.01 |
| 13 | 0.476 | 0.331 | 0.099 | 0.002 7 | 0.005 | 3.98 |
| 14 | 0.478 | 0.335 | 0.101 | 0.002 0 | 0.005 | 3.93 |
| 15 | 0.481 | 0.341 | 0.104 | 0.003 4 | 0.005 | 3.89 |
由表 4和表 5可以看出, 将元器件之间的纵向间距从10 mm逐渐增大到15 mm, 电路板上的最大温度从351.1 K持续减小至348.5 K, 降低了2.6 K。温度均值、标准差、平滑度这3个评价性指标值也随着纵向间距的增大而减小, 速度均值、标准差、平滑度这3个评价性指标值随着纵向间距的增大而增大。这说明随着纵向间距的增大, 电路板整体的冷却效果越来越好, 同时温度分布也越来越均匀。温度场三阶矩值为负值, 说明此时温度主要分布在元器件附近, 即元器件周围的温度更高。速度场三阶矩值为正值, 说明元器件上方的空气流动速度较快, 能够更有效地冷却电路板, 与温度场分布相呼应。5种布局下一致性的值均相同, 说明在计算分析中的取值很均匀。
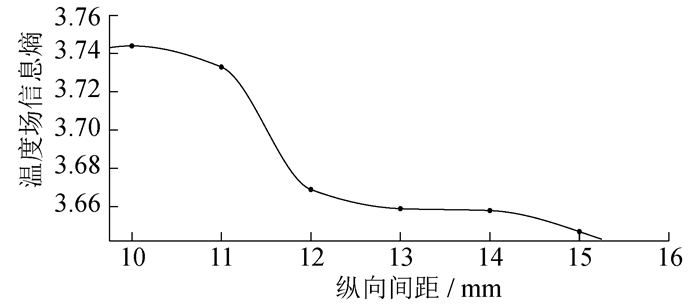
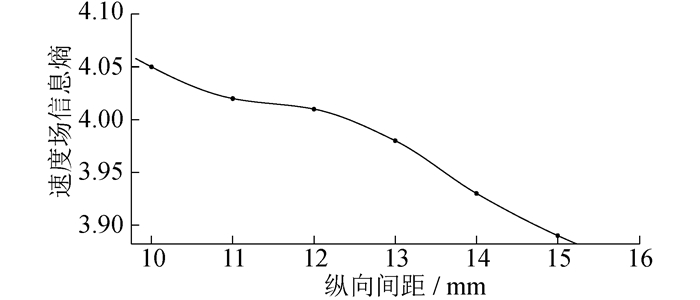
为了更好地观察信息熵值与纵向间距的关系, 拟合纵向间距与温度场、速度场的信息熵, 结果如图 7和图 8所示。
由图 7可以看出, 温度场信息熵与纵向间距成反比, 信息熵值随着纵向间距的增大而减小, 即当纵向间距为10 mm时电路板上的温度场分布的随机性最大。
由图 8可以看出, 速度场信息熵与纵向间距成反比, 信息熵值随着纵向间距的增大而减小, 这说明增大纵向间距会使电路板上速度场分布的随机性越来越小。
3.2.2 不同横向间距下的评价性指标
固定元器件间的纵向间距, 横向移动同侧的LSI和SSI的位置, 得到电路板的温度场和速度场分布图, 计算对应的信息熵等评价性指标, 结果如表 6和表 7所示。
表 6
不同横向间距下温度场的最大温度及评价性指标
| 横向间距/mm | 最大温度/K | 均值/K | 标准差 | 平滑度 | 三阶矩 | 一致性/×10-5 | 信息熵 |
| 10 | 351.1 | 333.04 | 18.1 | 0.996 9 | -3 763 | 5.20 | 3.72 |
| 11 | 350.6 | 332.97 | 17.9 | 0.996 9 | -3 584 | 5.20 | 3.74 |
| 12 | 349.4 | 332.96 | 17.8 | 0.996 8 | -3 448 | 5.20 | 3.75 |
| 13 | 350.9 | 332.92 | 17.6 | 0.996 8 | -3 306 | 5.20 | 3.77 |
| 14 | 350.7 | 332.93 | 17.5 | 0.996 8 | -3 207 | 5.20 | 3.73 |
| 15 | 350.5 | 332.91 | 17.4 | 0.996 7 | -3 138 | 5.20 | 3.71 |
表 7
不同横向间距下速度场的评价性指标
| 横向间距/mm | 均值/(m·s-1) | 标准差 | 平滑度 | 三阶矩 | 一致性 | 信息熵 |
| 10 | 0.471 | 0.322 3 | 0.094 1 | 0.004 0 | 0.005 | 4.053 |
| 11 | 0.464 | 0.321 5 | 0.093 7 | 0.003 0 | 0.005 | 4.041 |
| 12 | 0.453 | 0.320 9 | 0.093 4 | 0.001 2 | 0.005 | 4.034 |
| 13 | 0.460 | 0.322 7 | 0.094 3 | 0.002 7 | 0.005 | 4.031 |
| 14 | 0.467 | 0.319 9 | 0.092 8 | 0.004 3 | 0.005 | 4.036 |
| 15 | 0.453 | 0.321 0 | 0.093 4 | 0.001 9 | 0.005 | 4.021 |
由表 6和表 7可以看出, 当横向间距发生变化时, 电路板的最大温度均比初始温度351.1 K低, 且两者并无线性关系。当纵向间距为12 mm时, 最大温度较初始温度降低了1.7 K。温度均值、标准差、平滑度均低于初始值, 说明增大横向间距能够提高电路板温度场分布的均匀性, 减小热应力损伤。温度场三阶矩值均为负值, 说明温度主要分布在元器件附近。速度均值与横向间距有线性关系, 总体较初始均值0.471 m/s低。标准差和平滑度也均较初始值低。当横向间距为14 mm时, 速度场的标准差和平滑度值最小, 这表示此时电路板上的速度场分布最均匀。速度场三阶矩值均为正值, 说明速度场主要分布在元器件上方。5种布局下一致性的值均相同, 说明在计算分析中的取值很均匀。
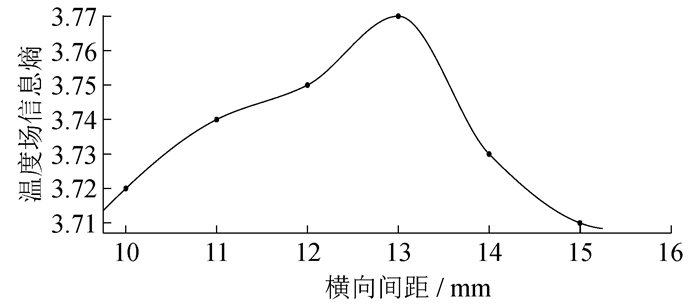
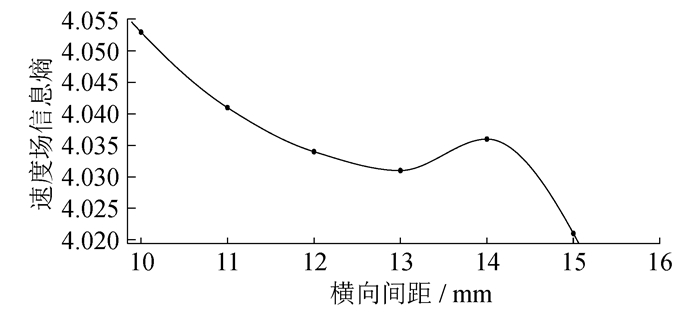
拟合纵向间距与温度场、速度场的信息熵, 结果如图 9和图 10所示。
由图 9可以看出, 温度场信息熵值的拟合曲线随横向间距的变化呈现为凸形, 随着横向间距的增大先增大后减小, 当间距为13 mm时, 达到最大值为3.77, 这说明此时电路板上温度场分布的随机性最大。
由图 10可以看出, 速度场信息熵大体是随着横向间距的增大而减小的。这说明增大横向间距可以减小电路板上速度分布的随机性。
4 结论
结合有限元法计算出电路板温度场和速度场分布图, 并使用信息熵等评价性指标对温度场和速度场分布图进行量化分析, 可以更为直观地研究电路板的冷却效果。
(1) 对不同布局的电路板进行热分析, 从电路板的温升来看, 并排布局的冷却效果优于叉排, LSI位于入口处的冷却效果优于SSI位于入口处, 因此应该尽量增大元器件间的纵向间距, 并选择一个合适的横向间距。
(2) 当各个布局下的温升均符合要求时, 应当结合各个评价性指标, 尽量选择标准差和信息熵值较小的布局, 以确保温度场和速度场分布的均匀性、有序性, 能更有效地避免热应力对电路板造成危害。
参考文献
-
[1]赵晨飞, 丁芸. 电路板的设计及印制[J]. 网印工业, 2012(6): 31-34.
-
[2]刘维红, 李丹. PCB板级电路中高效散热结构的优化设计[J]. 半导体光电, 2018, 39(5): 690-693.
-
[3]苏佩琳, 李涛, 彭雄奇. PCB焊点热循环失效分析和改进设计[J]. 应用数学和力学, 2015, 36(4): 414-422.
-
[4]隋越. 微型功率电路板强制对流冷却模拟[J]. 重庆文理学院学报(自然科学版), 2012, 31(1): 50-52.
-
[5]杨杰, 王艳. 基于COMSOL的电子元件散热数值模拟[J]. 农业装备与车辆工程, 2020, 58(12): 141-144.
-
[6]张安勤, 吴蕊, 张挺. 基于信息熵的异常检测算法[J]. 上海电力大学学报, 2020, 36(4): 386-390. DOI:10.3969/j.issn.2096-8299.2020.04.012
-
[7]吴子牛. 计算流体力学基本原理[M]. 北京: 科学出版社, 2001: 42-45.
-
[8]令狐克均, 饶应明, 刘忠翔, 等. 计算模块印制电路板的热设计和热仿真分析[J]. 机电信息, 2019(20): 81-83.
-
[9]龚红菊, 姬长英. 基于图像处理技术的麦穗产量测量方法[J]. 农业机械学报, 2007(12): 116-119.