|
|
|
发布时间: 2022-10-25 |
综合智慧能源 |
|
|
|
收稿日期: 2022-04-02
中图法分类号: TM715
文献标识码: A
文章编号: 2096-8299(2022)05-0483-05
|
摘要
为了保证综合能源系统(IES)的运行效率和可靠性, 能源需求的准确预测至关重要。提出了一种基于Pearson相关系数(PCC), 长短期记忆(LSTM)神经网络和多任务学习(MTL)的多元负荷预测方法。首先, 运用PCC选取与冷热电负荷相关性较大的影响因素作为模型的输入; 然后, 通过LSTM建立MTL的共享层, 实现多元负荷的联合预测; 最后, 结合亚利桑那州立大学的实测多元负荷数据来测试所提模型的预测精度。结果表明: 所提模型具有更高的预测精度。
关键词
综合能源系统; 多元负荷预测; Pearson相关系数; 长短时记忆网络; 多任务学习
Abstract
To ensure the operational efficiency and reliability of the Integrated Energy System(IES), accurate forecasting of energy demand has become a crucial task.Therefore, this paper proposes a multi-energy load prediction method based on Pearson Correlation Coefficient (PCC), Long and Short-Term Memory (LSTM) neural network, and Multi-Task Learning (MTL).First, the PCC is used to select the influencing factors that have a greater correlation with the cooling, heat, and electrical load as the input of the model.Then a shared layer of multi-task learning is established through the LSTM to realize the prediction of multi-energy load.Finally, combined with the measured multivariate load data of Arizona State University, the prediction accuracy of the proposed model is tested.The results show that the proposed model has higher prediction accuracy.
Key words
integrated energy system; multi-energy load forecasting; Pearson correlation coefficient; long and short-term memory neural network; multi-task learning
随着社会经济的快速发展, 能源利用与环境保护的协调发展面临重大挑战[1]。在此基础上, 构建清洁高效的综合能源系统(Integrated Energy System, IES)以提高能源利用效率、减少碳排放成为当务之急。IES作为一种新型能源供应模式, 通过冷、热、电等多种能源形式的耦合, 实现多种能源类型的灵活转换、高效分配和有机协调[2]。准确的多元负荷短期预测是IES可靠、经济运行的前提[3]。
目前, 针对单一负荷预测已取得较多成果。在电力负荷预测方面, 人工神经网络[4]、支持向量回归[5]、长短期记忆(Long and Short-Term Memory, LSTM)神经网络[6]等常被用于电力负荷预测。李文武等人[7]提出了一种基于多阶段优化的变分模态分解和粒子群算法优化支持向量回归的短期电力负荷预测模型。李婧等人[8]提出了一种基于遗传算法和传统径向基函数的短期电力系统负荷预测方法。在冷/热负荷预测方面, LI A等人[9]利用LSTM神经网络和注意力机制来预测建筑的冷负荷消耗。LING J H等人[10]采用反向传播神经网络模型和支持向量回归模型来预测建筑热负荷需求。
在IES多元负荷预测方面, 吴伟杰等人[11]首先利用变分模态分解方法对冷热电负荷进行分解, 然后采用样本熵对分解后模态分量进行重构, 最后采用纵横交叉算法优化深度信念网络对重构后的分量进行预测。李守茂等人[12]提出了一种基于改进粒子群算法和小波神经网络的IES短期负荷预测方法。然而, 由于不同负荷之间的耦合特性被忽略, 这些方法不能直接应用于IES多元负荷预测, 因此在现有研究基础上, 本文提出一种新的IES多元负荷预测模型。首先, 运用Pearson相关系数(Pearson Correlation Coefficient, PCC), 选取与冷热电负荷相关性较大的影响因素作为模型的输入, 然后将其输入到由LSTM神经网络构成的多任务学习(Multi-Task Learning, MTL)共享层中, 充分挖掘多元负荷数据的复杂耦合信息, 用以提高预测精度。
1 基本原理
1.1 PCC
为了提高模型的预测精度并降低预测的复杂度, 采用PCC来评估两个正态连续变量之间的线性相关性。该变量在-1和1之间变化[13], 两变量的相关系数rxy可表示为
| $ {r_{xy}} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)} \left( {{y_i} - \bar y} \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }} $ | (1) |
式中: x, y——变量xi和yi的均值。
变量的相关程度由相关系数的绝对值决定, 绝对值越大, 相关性越强。本文使用的相关系数分类如表 1所示。
表 1
相关系数范围
| |rxy| | 相关程度 |
| [0, 0.2] | 无关或弱相关 |
| [0.2, 0.5] | 中度相关 |
| [0.5, 1] | 强相关 |
1.2 LSTM神经网络
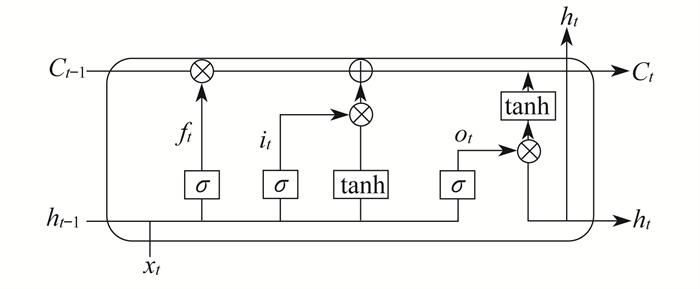
LSTM神经网络结构如图 1所示。LSTM神经网络基于循环神经网络(Recurrent Neural Network, RNN)的结构, 通过添加输入门、遗忘门和输出门来学习时间序列中的长期和短期依赖信息[14]。输入门用于确定在当前时刻应该向记忆元胞添加多少最新信息; 遗忘门用于决定可以丢弃多少先前的信息; 输出门旨在更新记忆元胞的状态并输出更新后的结果。
输入门信息it由输入值xt和t-1时刻的隐藏层输出值ht-1组成。输入门信息it和记忆单元的候选状态
| $ {i_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{\rm{i}}}\left[ {{h_{t - 1}}, {x_t}} \right] + {\mathit{\boldsymbol{b}}_{\rm{i}}}} \right) $ | (2) |
| $ {\hat C_t} = \tanh \left( {{\mathit{\boldsymbol{w}}_{\rm{c}}}\left[ {{h_{t - 1}}, {x_t}} \right] + {\mathit{\boldsymbol{b}}_{\rm{c}}}} \right) $ | (3) |
式中: Wi——输入门在t时刻的权重矩阵;
wc——t时刻候选状态的权重矩阵;
bi, bc——偏置向量;
σ, tanh——Sigmoid激活函数和tanh激活函数。
遗忘门信息ft由输入值xt和t-1时刻的隐藏层输出值ht-1组成。其计算公式如下
| $ {f_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{\rm{f}}}\left[ {{h_{t - 1}}, {x_t}} \right] + {\mathit{\boldsymbol{b}}_{\rm{f}}}} \right) $ | (4) |
式中: Wf, bf——遗忘门在t时刻的权重矩阵和偏置向量。
基于输入门和遗忘门的作用, 记忆单元Ct完成其状态的更新。其计算公式如下
| $ {C_t} = {f_t}{C_{t - 1}} + {i_t}{\hat C_t} $ | (5) |
式中: Ct-1——记忆单元Ct在上一时刻的状态值。
输出门信息ot由输入值xt和t-1时刻的隐藏层输出值ht-1组成。其计算公式如下
| $ {o_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{\rm{o}}}\left[ {{h_{t - 1}}, {x_t}} \right] + {\mathit{\boldsymbol{b}}_{\rm{o}}}} \right) $ | (6) |
式中: Wo, bo——输出门在t时刻的权重矩阵和偏置向量。
隐藏层输出值ht由输出门信息ot和记忆单元的状态值Ct计算得出。其计算公式如下
| $ {h_t} = {o_t}\tanh \left( {{C_t}} \right) $ | (7) |
1.3 MTL
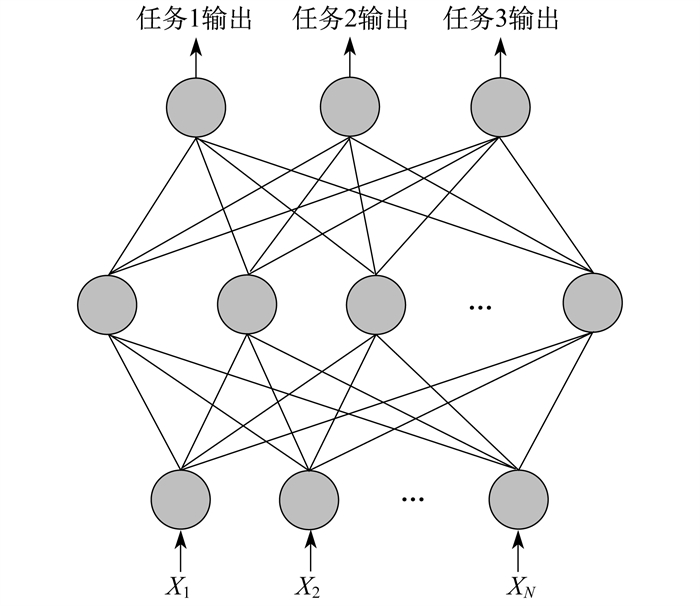
IES中不同的能源系统通过能量转换元件的能量流形式进行耦合, 数据中存在大量关于能量转换的共享特征。这些特征难以用传统的人工特征方法提取。MTL通过共享信息来学习和获取多个相关问题的知识, 能够有效利用IES复杂的能量转换共享信息[15]。MTL在处理一个问题的过程中可以通过使用共享层来学习, 并获得其他相关子任务所提供的辅助耦合信息, 进而达到提高模型输出精度与增强泛化能力的目的。MTL的共享机制结构如图 2所示。其中, X1, X2, X3, …, XN为输入。
MTL包含一组任务yt(t∈T)和数据集xi, yi1, yi2, yi3, …, yit, …, yiT (i=1, 2, 3, …, N), 其中T和N分别代表任务和数据样本的数量。预测函数定义为ft(x; θsh, θt): x→yt, 其中θsh和θt代表不同任务共享的参数和任务相关参数。MTL的整体优化损失函数可以定义如下
| $ \min \sum\limits_{t = 1}^T {{w^t}} {\hat L^t}\left( {{\theta ^{{\rm{sh}}}}, {\theta ^t}} \right) $ | (8) |
式中: wt——权重系数;
2 模型构建
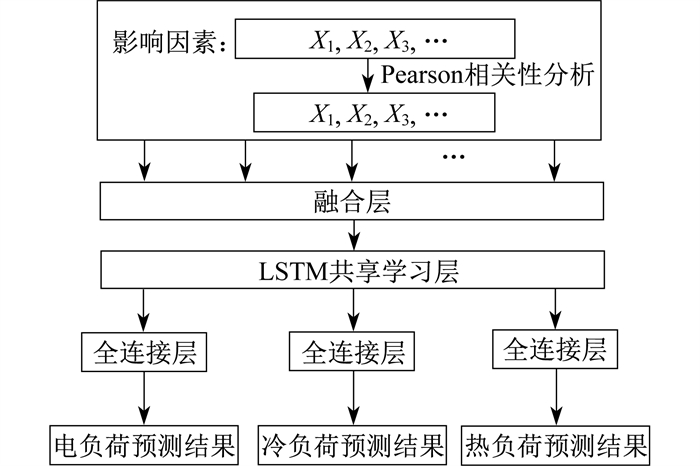
本文提出的基于PCC-LSTM-MTL的综合能源系统多元负荷预测模型如图 3所示。首先利用PCC选出合适的因素作为模型的输入变量, 然后将其输入到由LSTM神经网络构成的MTL共享层中, 充分挖掘多元负荷数据的复杂耦合信息, 提高预测精度。
3 算例分析
本文选择亚利桑那州立大学的Campus Metabolism系统所提供的Tempe校区电、冷、热负荷历史数据作为实验数据[16], 所有数据采样时间为2019年1月1日0时至2019年12月31日24时, 其中以2019年12月负荷数据为测试集, 剩余数据的80 % 为训练集, 20 % 为验证集。
3.1 输入特征
除了考虑负荷间的耦合关系外, 多元负荷预测还应考虑天气因素和日类型[17]。然而, 过多的输入特征不仅不利于网络训练, 而且增加了计算负担。因此, 应合理量化各个特征对负荷的影响程度, 筛选出影响不大的特征。本文采用PCC分析计算冷、热、电负荷与各个特征之间的相关性, 结果如表 2所示。
表 2
各影响因素的相关系数
| 影响因素 | 电负荷 | 冷负荷 | 热负荷 |
| 电负荷 | 1.000 | 0.873 | -0.695 |
| 冷负荷 | 0.873 | 1.000 | -0.784 |
| 热负荷 | -0.695 | -0.784 | 1.000 |
| 干球温度 | 0.812 | 0.933 | -0.871 |
| 湿球温度 | 0.443 | 0.459 | -0.408 |
| 相对湿度 | -0.419 | -0.488 | 0.521 |
| 风速 | 0.180 | 0.198 | -0.134 |
| 大气压力 | -0.508 | -0.504 | 0.600 |
因为本文采用MTL, 只要其中一个相关系数大于0.5, 就将该因子设置为输入特征。由于日类型仅用于分类, 不参与相关系数的计算, 因此本文将电负荷、冷负荷、热负荷、干球温度、大气压力和日类型设置为模型的输入特征, 其中日类型包括小时数和节假日信息。
3.2 评价指标
为了反映本文提出的模型的预测性能, 选取平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为评价指标。这两个评价指标定义如下
| $ {\rm{RMSE}} = \sqrt {\frac{1}{M}\sum\limits_{i = 1}^N {{{\left( {{y_i} - y_i^\prime } \right)}^2}} } $ | (9) |
| $ {\rm{ MAPE }} = \frac{1}{M}\sum\limits_{i = 1}^N {\frac{{\left| {{y_i} - y_i^\prime } \right|}}{{{y_i}}}} \times 100\% $ | (10) |
式中: yI——实际负荷值;
y′i——预测负荷值;
M——样本总数。
3.3 超参数选择
3.4 实验结果分析
为了验证PCC-LSTM-MTL模型在IES多元负荷预测场景中的优越性, 将LSTM-MTL和LSTM模型设置为对比模型。计算各种方法在测试集上的MAPE和RMSE指标, 结果如表 3所示。其中, PCC-LSTM-MTL取得了最好的预测效果, LSTM-MTL次之, 未采用PCC和MTL的LSTM模型效果最差。以电负荷预测为例, 相比于MTL-LSTM和LSTM, PCC-LSTM-MTL的RMSE分别降低了7.93 % 和9.52 %, MAPE分别降低了5.71 % 和13.46 %。
表 3
模型精度对比
| 模型 | 电/冷/热 | |
| RMSE/MW | MAPE/% | |
| PCC-LSTM-MTL | 0.627/0.534/0.129 | 2.873/3.992/3.067 |
| LSTM-MTL | 0.681/0.602/0.134 | 3.047/4.895/3.242 |
| LSTM | 0.693/0.737/0.142 | 3.320/6.519/3.437 |
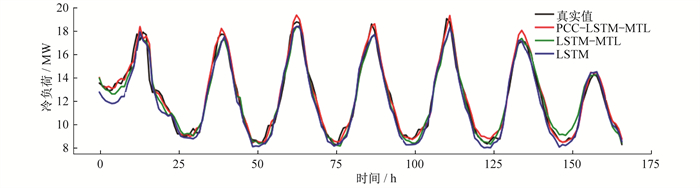
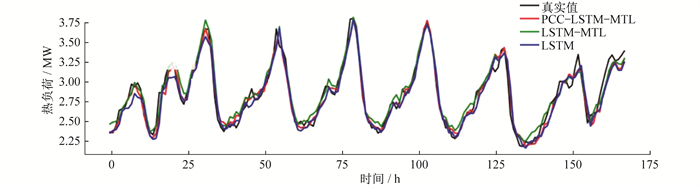
截取2019年12月8号0时至2019年12月15号24时预测结果如图 4~图 6所示。从结果来看, PCC-LSTM-MTL和LSTM-MTL模型对电、热、冷负荷的预测整体都比较准确, 但在峰谷时刻负荷波动较大时, PCC-LSTM-MTL模型能更加准确。
PCC-LSTM-MTL模型首先通过PCC提取与电、冷、负荷相关性较大的输入特征, 然后利用共享层学习多元负荷之间的复杂耦合信息, 在单一负荷波动较大时能够有效利用学习到的耦合特征来减少预测误差, 更好地拟合出负荷变化趋势。
4 结论
本文针对IES提出了一种基于PCC-LSTM-MTL的多元负荷预测方法, 并以亚利桑那州立大学Tempe校区电、冷、热负荷历史数据作为实际算例, 得出以下结论。
(1) 与LSTM模型相比, LSTM-MTL和PCC-LSTM-MTL模型通过共享层模拟冷、热、电负荷间的耦合特性, 有效提高了预测精度。
(2) 相比于LSTM-MTL模型, PCC-LSTM-MTL模型采用了PCC选取合适的影响因素作为输入变量, 提升了输入变量与目标变量的相关性, 使得模型的整体预测性能更好。
参考文献
-
[1]朱继忠, 董瀚江, 李盛林, 等. 数据驱动的综合能源系统负荷预测综述[J]. 中国电机工程学报, 2021, 41(23): 7905-7924.
-
[2]NIU D, YU M, SUN L, et al. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism[J]. Applied Energy, 2022, 313: 118801. DOI:10.1016/j.apenergy.2022.118801
-
[3]孙庆凯, 王小君, 张义志, 等. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63-70.
-
[4]ROMÁN-PORTABALES A, LÁPEZ-NORES M, PAZOS-ARIAS J J. Systematic review of electricity demand forecast using ANN-based machine learning algorithms[J]. Sensors (Basel), 2021, 21(13): 4544. DOI:10.3390/s21134544
-
[5]NIE H, LIU G, LIU X, et al. Hybrid of ARIMA and SVMs for short-term load forecasting[J]. Energy Procedia, 2012, 16: 1455-1460. DOI:10.1016/j.egypro.2012.01.229
-
[6]KONG W C, DONG Z Y, JIA Y W, et al. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 841-851. DOI:10.1109/TSG.2017.2753802
-
[7]李文武, 石强, 李丹, 等. 基于VMD和PSO-SVR的短期电力负荷多阶段优化预测[J]. 中国电力, 2022, 55(8): 171-177.
-
[8]李婧, 田龙威, 王艳青. 基于GARBF神经网络的电力系统短期负荷预测[J]. 上海电力学院学报, 2019, 35(3): 205-210.
-
[9]LI A, XIAO F, ZHANG C, et al. Attention-based interpretable neural network for building cooling load prediction[J]. Applied Energy, 2021, 299: 117238. DOI:10.1016/j.apenergy.2021.117238
-
[10]LING J H, DAI N, XING J C, et al. An improved input variable selection method of the data-driven model for building heating load prediction[J]. Journal of Building Engineering, 2021, 44: 103255. DOI:10.1016/j.jobe.2021.103255
-
[11]吴伟杰, 吴杰康, 雷振, 等. CCHP用户冷热电负荷预测的纵横交叉优化深度信念网络方法[J]. 南方电网技术, 2021, 15(12): 1-10.
-
[12]李守茂, 戚嘉兴, 白星振, 等. 基于IPSO-WNN的综合能源系统短期负荷预测[J]. 电测与仪表, 2020, 57(9): 103-109.
-
[13]刘倩倩, 刘钰山, 温烨婷, 等. 基于PCC-LSTM模型的短期负荷预测方法[J/OL]. 北京航空航天大学学报: 1-11(2021-07-14)[2022-03-18]. DOI: 10.13700/j.bh.1001-5965.2021.0145.
-
[14]HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995.
-
[15]ZHANG G, BAI X Q, WANG Y X. Short-time multi-energy load forecasting method based on CNN-Seq2Seq model with attention mechanism[J]. Machine Learning with Applications, 2021, 5: 100064.
-
[16]张涌新, 沈弘, 马静. 综合能源系统负荷特性分析及应用研究[J]. 电力建设, 2018, 39(9): 18-29.
-
[17]ZHANG L J, SHI J S, WANG L L, et al. Electricity, heat, and gas load forecasting based on deep multitask learning in Industrial-park integrated energy system[J]. Entropy (Basel), 2020, 22(12): 1355.
-
[18]栗然, 孙帆, 丁星, 等. 考虑多能时空耦合的用户级综合能源系统超短期负荷预测方法[J]. 电网技术, 2020, 44(11): 4121-4134.
-
[19]HE F F, ZHOU J Z, FENG Z K, et al. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm[J]. Applied Energy, 2019, 237: 103-116.