|
|
|
发布时间: 2022-10-25 |
综合智慧能源 |
|
|
|
收稿日期: 2022-04-02
基金项目: 上海市科委节能减排专项——上海市热交换系统节能工程技术中心项目(17DZ2282800)
中图法分类号: TK267
文献标识码: A
文章编号: 2096-8299(2022)05-0478-05
|
摘要
多台热电联产机组组成的复杂热电联产(CHP)系统优化过程中会使得搜索域增大, 优化收敛速度变慢。针对这一问题。通过借鉴内点法将原搜索范围进行离散、组合, 从而将搜索范围进行合理收缩, 提高了算法在寻优过程中的收敛速度, 并使优化结果更接近全局最优。将改进遗传算法应用于某石化企业自备电厂的复杂CHP系统, 并通过仿真模拟对优化结果进行验证。结果表明, 改进遗传算法可以有效提高遗传算法的收敛速度和优化结果。
关键词
改进遗传算法; 负荷优化调度; 热电联产; 复杂系统; 优化搜索域
Abstract
In the process of optimization of complex combined heat and power(CHP) system composed of several combined heat and power units, the search area will be enlarged and the convergence speed will be slow.To solve this problem, the search area of genetic algorithm is optimized.By using interior point method for reference, the original search range is discretized and combined, and the search range is reduced reasonably, so as to improve the convergence speed of the algorithm in the process of optimization and make the optimization result closer to the global optimum.The improved algorithm is applied to the complex CHP system of a petrochemical enterprise's own power plant and the optimization results are verified by simulation.The results show that the improved genetic algorithm can effectively improve the convergence speed and optimization results of the genetic algorithm.
Key words
improved genetic algorithm; load optimal scheduling; combined heat and power; complex system; optimization search domain
热力系统的负荷优化调度是通过调整各台机组的负荷(热负荷、电负荷), 使机组实现最优运行。常见的机组负荷优化调度方法有等微增率法[1-3]、线性规划法[4]、动态规划法[5]等。这些优化方法通常要求机组的运行曲线是连续且上凹的, 然而实际机组的运行曲线并不能完全满足条件[6]。尤其是对于多台不同类型的热电联产(Combined Heat and Power, CHP)机组组成的复杂热电联产系统, 其运行曲线通常为非凸函数, 因此采用这类优化方法并不能很好地求得最优解。
遗传算法作为仿生优化算法, 通过模仿生物基因遗传过程, 在搜寻范围内, 利用基因复制、重组、变异过程, 寻找待解问题的最优解[7]。由于遗传算法的优化过程并不要求系统运行曲线为连续凸函数, 因此在机组负荷优化调度中具有一定优势。遗传算法具有鲁棒性好、适用性广等特点, 使得在求解各类优化问题时, 采用遗传算法可以得到近似最优解。然而在求解最优化问题的过程中, 通常希望优化结果尽可能接近全局最优解, 收敛速度尽可能快。遗传算法是通过随机寻优的方式选取大量的候选解形成“种群”, 在大量的种群中寻找最优。复杂CHP系统中实际热力系统中机组的台数较多, 优化变量多, 使得遗传算法的寻优范围增大, 导致优化求解的计算量大大增加, 优化速度下降, 优化结果难以接近全局最优[8]。因此在复杂CHP系统负荷的优化调度中, 通过改进遗传算法提高寻优速度很有必要。本文对遗传算法进行改进, 并应用于某石化企业自备电厂的复杂CHP系统, 以期为系统负荷的优化调度提供一定参考。
1 优化调度数学模型
根据企业自备电厂的要求, 负荷优化调度的优化目标是在保证一定约束条件下实现多台CHP机组构成的复杂CHP系统发电功率最大。其约束条件要考虑用户供热负荷、供热参数、单机煤耗率、平均煤耗率等。
在优化过程中, 为保证单台机组的发电功率最大, 需要对机组的主蒸汽流量进行约束。当机组热负荷较低时, 由于发电机出力限制, 机组的主蒸汽流量受到约束, 此时以满足发电机最大出力的主蒸汽流量为该热负荷下最大主蒸汽流量。当机组热负荷增大时, 机组受到汽轮机最大进汽量限制, 此时机组的最大主蒸汽流量为汽轮机最大进汽量。热力系统优化模型如下。优化目标为
| $ \max N = \sum\limits_{i = 0}^n {{N_i}} $ | (1) |
式中:
maxN——最大发电功率, MW;
Ni——i#机发电功率, MW。
约束条件为
| $ {\bar b_s} \le 305 $ | (2) |
| $ {b_{si}} \le 310 $ | (3) |
| $ \sum\limits_{i = 0}^n {D_i^{\rm{L}}} = D_{\rm{g}}^{\rm{L}} $ | (4) |
| $ \sum\limits_{i = 0}^n {D_i^{\rm{M}}} = D_{\rm{g}}^{\rm{M}} $ | (5) |
| $ P_i^{\rm{L}} \ge \min P_{\rm{g}}^{\rm{L}} $ | (6) |
| $ P_i^{\rm{M}} \ge \min P_{\rm{g}}^{\rm{M}} $ | (7) |
| $ D_{\min }^0 \le D_i^0 \le D_{\max }^0 $ | (8) |
式中: bs——系统平均煤耗率, g/kWh;
bsi——i#机组的煤耗率, g/kWh;
DiL——i#机低压供热蒸汽量, t/h;
DgL——低压供热蒸汽总量, t/h;
DiM——i#机中压供热蒸汽量, t/h;
DgM——中压供热蒸汽总量, t/h;
PiL——i#机低压供热蒸汽压力, MPa;
minPgL——低压供热蒸汽最低压力, MPa;
PiM——i#机中压供热蒸汽压力, MPa;
minPgM——中压供热蒸汽最低压力, MPa;
Di0——i#机组的主蒸汽流量, t/h;
Dmin0——机组最小主蒸汽流量, t/h;
Dmax0——机组最大主蒸汽流量, t/h。
2 改进遗传算法
由于复杂CHP系统负荷调度问题变量多、约束多, 同时约束条件、优化变量之间存在一定的耦合, 使得寻优过程变得更加复杂。当采用遗传算法进行寻优时时, 优化收敛速度很慢, 优化结果不理想, 因此需要对遗传算法进行改进。
针对遗传算法的改进, 大量的学者进行了研究。文献[8]通过引进蒙特卡洛抽样算法对遗传算法的候选解进行优化, 提高了算法的寻优收敛速度和寻优精度, 能很好地应用于火电厂的灵活调度问题。文献[9]通过改进其交叉遗传变异算子, 修正了所有解集, 提高了寻优的稳定性和收敛性。文献[10]引入自适应策略, 改进遗传算法的变异算子, 并将其应用于以环境成本和运行维护成本最小为优化目标的调度问题上, 提升了遗传算法的寻优稳定性。文献[11]针对机组动态负荷分配问题, 提出了改进的实数编码遗传算法, 提高了求解的收敛速度和最优解精度。文献[12]引入线性递减的惯性权重对粒子群算法进行改进, 将改进
后的粒子群优化算法应用到以发电成本最小为优化目标的CHP负荷优化调度中, 提升了目标值最优和收敛速度。文献[13]通过改进蜂群优化算法对CHP进行负荷优化经济分配, 收敛速度更快且优化结果更接近最优。文献[14]通过改进混沌离散粒子群算法, 避免了在负荷优化调度寻优过程中的早熟问题, 提高了求解精度。文献[15]对粒子群算法进行优化改进, 提出了一种差分进化-交叉量子粒子群优化算法(DE - CQPSO), 在考虑环境约束的复杂优化调度问题时, 能有效提高优化算法的鲁棒性, 提高优化精度。
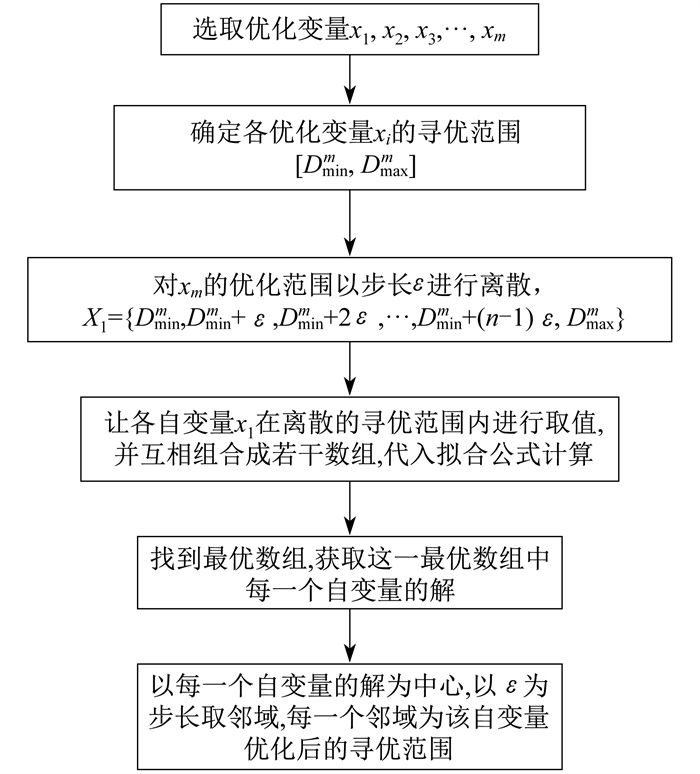
上述改进策略都是通过对遗传算法内部的交叉算子、筛选算子、变异算子等进行调整改进, 从而适应相应的优化问题, 在一定程度上提高了算法的寻优能力。然而, 改进内部算子的方式其编码过程比较复杂, 改进后的算法只能针对特定问题使用, 普适性较差; 同时, 当整体系统的优化变量与优化目标及约束条件存在耦合关系时, 求解过程的收敛时间会增加, 优化结果会受到一定影响。遗传算法通过模仿基因的复制、交叉、变异在一定寻优范围内进行寻优搜索, 寻优范围的大小影响着寻优搜索的速度和精度。若能有效缩小寻优范围, 则能有效提升遗传算法的寻优效率。因此, 通过借鉴枚举法和内点法的寻优过程, 本文提出了有效缩小遗传算法优化搜索范围的方法。该方法是在确定寻优范围后, 对该寻优范围以离散代入计算的方式进行预处理, 从而得到更精确的优化范围。改进遗传算法优化搜索范围流程如图 1所示。
由图 1可知, 该改进策略是通过对所有自变量的定义域按一定的步长ε进行离散, 将各个自变量的离散点通过约束进行组合并代入机组运行曲线中计算, 得出各离散点组合的解并选出最优离散点组合。此时, 最优离散点组合中的各个自变量都是近似最优解。选取各自变量近似最优解周围步长ε的邻域作为遗传算法的寻优范围, 从而有效缩小优化搜索范围, 提高寻优精度和求解的收敛速度。
当函数曲线出现激增时, 离散的步长有可能出现过大的情况, 此时采用这一缩小寻优范围的方法容易使优化范围偏离最优解。然而对于热力系统的负荷优化调度而言, 因机组爬坡速率的限制, 热力系统的供热特性曲线一般不会出现大幅度的负荷激增现象, 因此该方法应用于热力系统负荷优化调度问题, 能有效缩小遗传算法的寻优范围。
3 改进遗传算法验证
为了验证改进遗传算法的可行性, 以某石化企业自备电厂的复杂CHP系统为例, 对该系统的负荷进行优化调度。该CHP系统共有5台机组, 0#机组为背压机(型号B25 - 90/13 - 1), 1#机组为单抽供热机组(型号C50 - 90/13), 4#机组为双抽供热机组(型号CC50 - 90/42/15), 5#机组和6#机组为双抽供热机组(型号CC100 - 8.83/3.8/1.47)。采用EBSILON建立复杂CHP系统的仿真模型, 通过仿真模拟, 获得系统在不同供热量和不同调度方案下的发电功率。式(1)~式(6)建立的优化模型和图 1给出的改进遗传算法通过MATLAB软件编程实现。
以中压供热需求量为250 t/h、低压供热为650 t/h时4机供热的典型供热工况为例, 以0#机组、1#机组、4#机组、5#机组为一号组合方案, 0#机组、4#机组、5#机组、6#机组为二号组合方案。利用遗传算法和改进遗传算法分别对两种方案进行调度优化, 发现一号组合方案中, 采用改进遗传算法进行优化调度后的最大发电功率为255.46 MW, 遗传算法为253.99 MW; 二号组合方案中, 采用改进遗传算法进行优化调度后的最大发电为功率为326.02 MW, 遗传算法为306.34 MW。优化结果如表 1与表 2所示。
表 1
一号组合方案优化结果
| 算法 | 供热状况 | ||||||||
| 0#背压排汽 | 1#低压供热 | 1#主蒸汽 | 4#中压供热 | 4#低压供热 | 4#主蒸汽 | 5#中压供热 | 5#低压供热 | 5#主蒸汽 | |
| 遗传算法 | 170.78 | 229.80 | 369.99 | 152.63 | 119.33 | 374.51 | 97.37 | 130.09 | 619.99 |
| 改进遗传算法 | 170.81 | 229.90 | 369.99 | 170.35 | 103.32 | 374.71 | 79.65 | 145.97 | 619.99 |
表 2
二号组合方案优化结果
| 算法 | 供热状况 | |||||||||
| 0#背压排汽 | 4#低压供热 | 4#中压供热 | 4#主蒸汽 | 5#中压供热 | 5#低压供热 | 5#主蒸汽 | 6#中压供热 | 6#低压供热 | 6#主蒸汽 | |
| 遗传算法 | 170.78 | 25.69 | 193.24 | 307.69 | 111.08 | 145.99 | 619.99 | 113.23 | 139.99 | 619.99 |
| 改进遗传算法 | 170.87 | 84.60 | 182.30 | 374.98 | 79.97 | 149.46 | 619.97 | 85.43 | 147.35 | 619.94 |
一号组合方案中, 采用改进遗传算法到进行优化调度后的最大发电功率相较于原遗传算法由原来的253.99 MW提高至255.46 MW, 提高了1.47 MW, 增长率为0.58 %。同样, 二号组合方案中, 采用改进遗传算法进行优化调度的最大发电功率相较于遗传算法提高了19.68 MW, 增长率为6.4 %。从两组优化结果改进遗传算法可以看出, 相较于遗传算法, 改进遗传算法的优化结果均有不同幅度的提高, 求解结果更优, 优化效果更好。
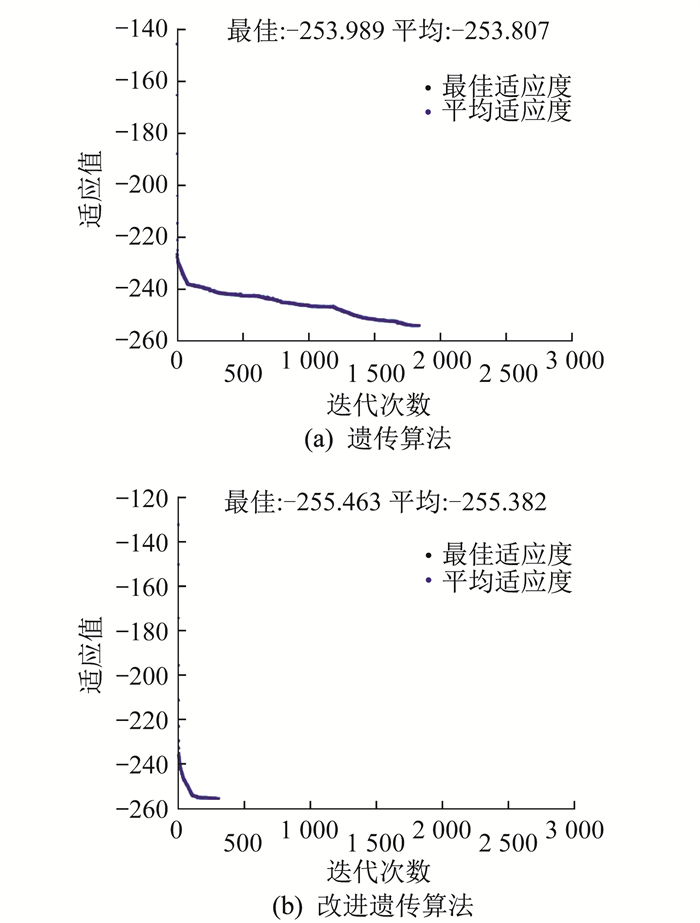
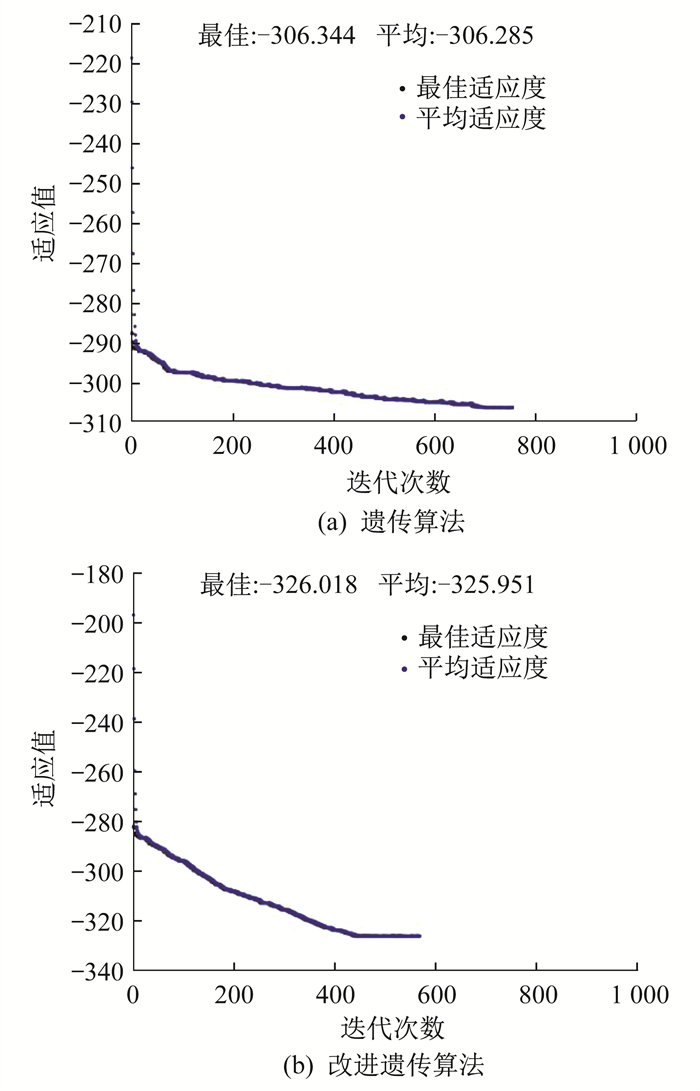
在求解最优的过程中, 求解速度也十分关键, 图 2和图 3为采用遗传算法和改进遗传算法的优化收敛图。
通过对比分析可以看出, 对一号组合方案采用遗传算法进行优化时, 其优化需要1887迭代实现收敛, 而采用改进遗传算法仅需要386迭代实现收敛, 优化速度提高了79.5 %; 对二号组合方案采用遗传算法进行优化时, 其优化需要768迭代实现收敛, 而采用改进遗传算法仅需要579迭代实现收敛, 优化速度提高了24.6 %。
通过上述优化结果和收敛结果可以看出, 针对复杂负荷优化调度问题采用改进遗传算法, 优化收敛速度有明显提升, 且在一定程度上, 优化结果更加接近全局最优解。
4 结论
本文针对遗传算法在复杂CHP系统负荷优化调度中优化速度较慢的问题, 借鉴内点法, 提出了合理缩小遗传算法寻优范围的改进方法, 并将改进后的遗传算法应用于某石化企业自备电厂的多机组CHP系统负荷优化调度中。通过仿真模拟对优化结果进行验证, 得出以下结论:
(1) 改进后的遗传算法可以有效提高遗传算法的收敛速度, 在典型热负荷下4机组合的两种方案中, 优化速度分别提升了79.5 % 和24.6 %。
(2) 改进后的遗传算法优化结果优于遗传算法, 在典型热负荷下4机组合的两种方案中, 最大发电功率分别提高了0.58 % 和6.4 %, 优化结果更加接近全局最优解。
参考文献
-
[1]童占北, 杨顺吉. 一种火电机组负荷经济分配的研究[J]. 科技风, 2020(1): 168-169.
-
[2]葛晓霞. 电厂负荷的最优分配[J]. 汽轮机技术, 1995(5): 299-230.
-
[3]王惠杰, 李鑫鑫, 范志愿. 考虑环境条件的燃机-蒸气联合循环机组节能优化调度[J]. 汽轮机技术, 2016, 58(1): 47-49. DOI:10.3969/j.issn.1001-5884.2016.01.014
-
[4]王惠杰, 范志愿, 李鑫鑫. 基于线性规划法和等微增率法的电厂负荷优化分配[J]. 电力科学与工程, 2016, 32(1): 1-5. DOI:10.3969/j.issn.1672-0792.2016.01.001
-
[5]甘超齐, 丁健, 赵伟. 火电厂厂级负荷优化分配系统设计及应用[J]. 热力发电, 2013, 42(8): 94-97. DOI:10.3969/j.issn.1002-3364.2013.08.094
-
[6]商灵默, 刘星. 基于遗传算法的火电厂机组间负荷分配的研究[J]. 潍坊学院学报, 2008, 8(4): 27-30. DOI:10.3969/j.issn.1671-4288.2008.04.009
-
[7]雷振, 韦钢, 沈芸, 等. 基于改进遗传算法的含分布式电源配电网重构[J]. 上海电力学院学报, 2011, 27(3): 233-237.
-
[8]PONCIROLI R, STAUFF N E, RAMSEY J, et al. An improved genetic algorithm approach to the unit commitment/economic dispatch problem[J]. IEEE Transactions on Power Systems, 2020, 35(5): 4005-4013. DOI:10.1109/TPWRS.2020.2986710
-
[9]ZOU D, LI S, KONG X, et al. Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy[J]. Applied Energy, 2019, 237: 646-670.
-
[10]JIANG H, NING S, GE Q, et al. Optimal economic dispatching of multi-microgrids by an improved genetic algorithm[J]. IET Cyber-Systems and Robotics, 2021, 3(1): 68-76.
-
[11]PATTANAIK J K, BASU M, DASH D P. Improved real coded genetic algorithm for dynamic economic dispatch[J]. Journal of Electrical Systems and Information Technology, 2018, 5(3): 349-362.
-
[12]郭民臣, 樊雪, 彭新飞, 等. 改进粒子群算法应用于热电联产负荷优化分配[J]. 汽轮机技术, 2013(3): 229-231.
-
[13]RABIEE A, JAMADI M, MOHAMMADI I B, et al. Optimal non-convex combined heat and power economic dispatch via improved artificial bee colony algorithm[J]. Processes, 2020, 8(9): 1-22.
-
[14]陈璟华, 周俊, 郭壮志, 等. 改进混沌离散粒子群与等微增率的机组组合优化[J]. 中国电力, 2014, 47(7): 6-11.
-
[15]ZHAO X G, LIANG J, MENG J, et al. An improved quantum particle swarm optimization algorithm for environmental economic dispatch[J]. Expert Systems with Applications, 2020, 152: 1-14.