1 实验系统与方法

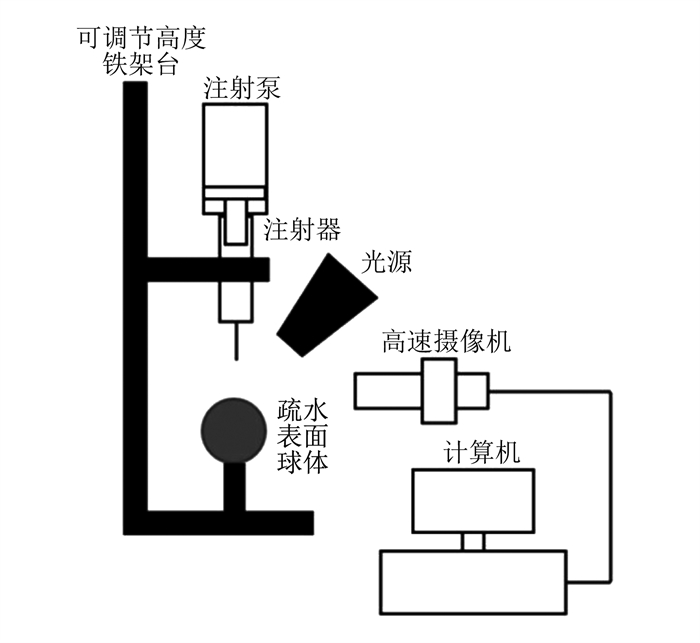
液滴撞击球面实验系统由计算机、高速摄像机、光源、注射泵、注射器、可调节高度铁架台和不同直径疏水表面球体组成, 具体如图 1所示。

图 1 实验系统

实验时由注射泵推动注射器产生液滴, 液滴自由落体撞击目标球体, 高速摄影机拍摄画面后传输到计算机后处理图片, 抓取数据。液滴撞击速度由调节掉落高度来控制。不同直径疏水球体是将玻璃球经过表面处理后得到, 制备得到的球面静态接触角为105°±3°, 属于疏水表面。实验过程中的参数表征如图 2所示。

图 2 实验各参数

选取液滴下降过程中最临近撞击时刻的连续相邻2张图片, 如图 2(a)所示。根据帧率计算连续相邻2张图片的时间间隔, 记为Δt, 液滴中心点在Δt内下降的高度记为Δx, 液滴速度v的计算公式为

$ v = \frac{{\Delta x}}{{\Delta t}} $

(1)

取相同工况下多次实验测得速度的平均值, 可认为是液滴撞击时的真实速度。

在液滴撞击固体表面的过程中, 液滴的铺展因子是表征液滴铺展行为的重要参数, 其计算公式为

$ {D^*} = \frac{d}{{{d_0}}} $

(2)

$ {d_0} = {\left( {{D_{\rm{V}}}D_{\rm{H}}^2} \right)^{\frac{1}{3}}} $

(3)

式中: D^*——液滴无量纲铺展因子;

d——液滴在疏水球面上的铺展直径, 即液滴在球面上所铺展的弧长;

d₀——液滴当量直径^[20];

D_V, D_H——液滴竖直直径和水平直径。

D_V和D_H如图 2(b)所示。经过多次测量取平均值, 实验中液滴当量直径为2.04 mm。液滴无量纲中心高度h^*是另一个表征液滴铺展行为的重要参数, 其计算公式为

$ {h^*} = \frac{h}{{{d_0}}} $

(4)

式中: h——液滴中心高度。

h如图 2(c)所示。另外, 无量纲时间定义t^*为

$ {t^*} = \frac{{tv}}{{{d_0}}} $

(5)

式中: t——液滴撞击时间, 液滴与表面接触时t=0。

液滴-球体直径比ε为

$ \varepsilon = \frac{{{d_0}}}{D} $

(6)

式中: D——撞击球体直径。

2 实验结果与分析

2.1 液滴撞击过程动态行为研究

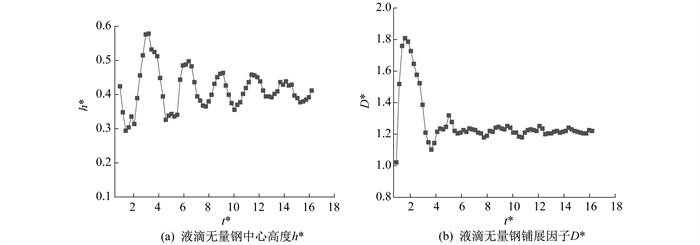
为研究液滴撞击疏水球面后的动态行为特征, 本文通过将液滴以不同速度撞击球体和相同直径液滴撞击不同直径球面开展了实验研究。图 3给出了液滴撞击疏水球面的动态演化过程(v=0.79 m/s, ε=0.30)。图 4是此工况下液滴撞击疏水球面行为特征的变化趋势。

图 3 液滴撞击疏水球面的动态演化过程

图 4 液滴撞击疏水球面行为特征的变化趋势

液滴撞击疏水球面后的行为大致可分为铺展、回缩和振荡-稳定3个阶段。铺展阶段从液滴下端接触球面开始, 液滴达到最大铺展结束。达到最大铺展同时回缩阶段开始, 当液滴铺展因子进行最大幅度缩小后且尚未重新增大时, 回缩阶段结束。振荡-稳定阶段液滴持续小幅振荡并最终趋于静止。当t^*=0时, 液滴与球面发生撞击, 以撞击点为圆心向四周铺展, 在铺展早期液滴上端依然保持球状, 在较短时间内球面出现表面波且呈阶梯状。随着铺展的进行, 液滴中心高度逐渐降低, 从凸起最终变为凹陷。最终液滴铺展因子达到最大值, D^*=1.81, 此时液滴中心高度低、边缘高, 液滴中心出现空气柱, 变为环状液滴, 如图 3(t^*=1.60时)所示。此时, 图 4中液滴无量纲铺展因子D^*最大, 液滴无量纲中心高度h^*最小。这是由于边缘液滴的动能已经耗尽, 而中心液滴在动能的驱使下依然向四周扩散, 导致中心液量减少从而凹陷。液滴铺展因子达到最大值后, 液滴的铺展阶段结束, 回缩阶段开始。在液滴表面能的作用下液滴回流, 中心部位重新升高, h^*由0.29增大到0.58, 从凹陷转为凸起, 直到液滴中心高度达到最大值。此时液滴铺展因子在回缩状态下可达到最小值, D^*=1.09, 液滴回缩阶段结束。之后液滴会经历多次的铺展-回缩的振荡周期, 并最终趋于平衡稳定状态。这就是振荡-稳定阶段。在此阶段, 液滴铺展因子小于铺展阶段结束时的最大值, 大于回缩状态结束时的最小值, 波动幅度逐渐减小趋于稳定, 回缩时的液滴中心高度小于最大值且随时间逐渐降低。由图 4可知, 经过多次振荡后, 液滴固液气三相接触线不再移动, 液滴铺展因子稳定时, D^*=1.22, 液滴上端振动幅度逐渐减小但振荡时间长于三相接触线, 液滴中心高度迟于液滴铺展因子达到稳定, 稳定时液滴中心高度为h^*=0.40。最终液滴静止在球面上呈椭球状, 达到平衡稳定状态。

2.2 撞击速度对液滴撞击行为特征的影响

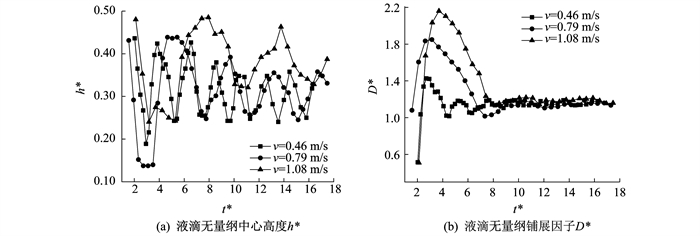
撞击速度对液滴撞击疏水球面后的行为特征有着明显的影响。图 5给出了液滴以不同速度撞击相同直径疏水球面的动态演化过程(ε=0.11)。图 6是不同速度下液滴撞击疏水球面行为特征的变化趋势。

图 5 液滴以不同速度撞击疏水球面的动态演化过程

图 6 液滴以不同速度撞击疏水球面特征的变化趋势

图 5中, 第1~3张为液滴的铺展阶段, 第4~5张为回缩阶段, 第6张为稳定状态。由图 6(a)可知, 液滴中心高度在撞击后经过多次振荡, 振荡幅度随撞击时间的增大而减小。由图 6(b)可知: 液滴铺展因子在液滴撞击球面后迅速增大, 达到最大值后减小并最终趋于稳定; 液滴铺展因子最大值与速度成正比, 撞击速度越大, 铺展因子最大值就越大, 撞击速度分别为0.46 m/s, 0.79 m/s, 1.08 m/s时, 铺展因子最大值分别为1.43, 1.85, 2.16;而不同撞击速度的液滴最终达到稳定状态时铺展因子较为接近, D^*的波动范围在1.13~1.18, 表面液滴动能对液滴的最终状态没有明显影响。对比图 6(a)和图 6(b)可以发现: 固液气三相接触线的稳定要早于上层液滴的稳定; 不同撞击速度时, 液滴铺展因子达到最大值的无量纲时间较为接近, 因此铺展速度随撞击速度的增大而增大, 且速度变化对铺展时间影响较小; 液滴撞击速度增加时, 液滴惯性力增大, 带来的动能增大, 液滴铺展因子最大值增大, 需要克服液滴黏性耗散所需的能量也增大; 动能转变而来的表面能也增大, 回缩阶段的液滴中心高度随之增加。

2.3 液滴球体直径比对液滴撞击行为的影响

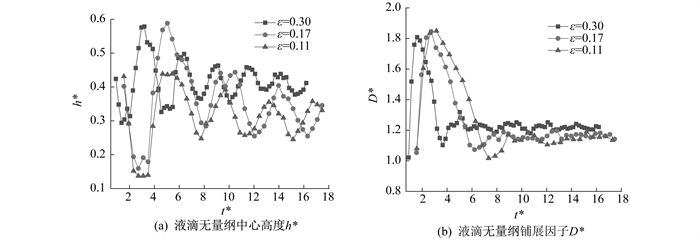
图 7为撞击速度v=0.79 m/s时, 液滴撞击不同直径疏水球面的动态演化过程。图 8为其动态演化过程中液滴撞击不同直径的疏水球面行为特征的变化趋势。

图 7 液滴撞击不同直径疏水球面的动态演化过程

图 8 液滴撞击不同直径疏水球面行为特征的变化趋势

由图 8(a)可知, 液滴中心高度经历多次振荡后趋于稳定, 撞击速度v相同、液滴-球体直径比ε不同时, 振荡周期和幅度都接近。由图 8(b)可知: 撞击速度v相同、液滴-球体直径比ε不同时, 液滴撞击球面铺展直径最大值与液滴-球体直径比ε呈反比, ε增大时, 液滴铺展直径最大值小幅减小, ε为0.11, 0.17, 0.30时, D^*分别为1.81, 1.85, 1.86;随着液滴-球体直径比ε的增大, 液滴各阶段持续时间减少, 振荡稳定阶段振荡幅度增大; 液滴-球体直径比ε不同时, 液膜在球面上最终稳定的铺展因子接近, 说明液滴撞击球面后, 最终稳定附着在球面的润湿面积差异较小。因此, 液滴-球体直径比ε增大对液滴撞击过程起到了促进的作用, 各阶段持续时间小幅度缩短, 除此之外, 并无明显影响。

3 结论

参考文献

[1]
WANG C H, TSAI H L, WU Y C, et al. Investigation of molten metal droplet deposition and solidification for 3D printing techniques[J]. Journal of Micromechanics and Microengineering, 2016, 26(9): 095012. DOI:10.1088/0960-1317/26/9/095012
[2]
HSIEH S S, LUO S Y. Droplet impact dynamics and transient heat transfer of a micro spray system for power electronics devices[J]. International Journal of Heat and Mass Transfer, 2016, 92: 190-205. DOI:10.1016/j.ijheatmasstransfer.2015.08.099
[3]
BRICEÑO D, GAETE-GARRETÓN L, ZANELLI-IGLESIAS C, et al. Ultrasonic atomization of distilled water[J]. The Journal of the Acoustical Society of America, 2018, 144(1): 222-227. DOI:10.1121/1.5045558
[4]
PALACIOS J, HERNÁNDEZ J, GÓMEZ P, et al. Experimental study of splashing patterns and the splashing/deposition threshold in drop impacts onto dry smooth solid surfaces[J]. Experimental Thermal and Fluid Science, 2013, 44: 571-582. DOI:10.1016/j.expthermflusci.2012.08.020
[5]
LIU X, ZHANG X, MIN J C. Spreading of droplets impacting different wettable surfaces at a Weber number close to zero[J]. Chemical Engineering Science, 2019, 207: 495-503. DOI:10.1016/j.ces.2019.06.058
[6]
LUO J, WU S Y, XIAO L, et al. Parametric influencing mechanism and control of contact time for droplets impacting on the solid surfaces[J]. International Journal of Mechanical Sciences, 2021, 197: 106333. DOI:10.1016/j.ijmecsci.2021.106333
[7]
HAO J G, LU J, LEE L N, et al. Droplet splashing on an inclined surface[J]. Physical Review Letters, 2019, 122(5): 054501. DOI:10.1103/PhysRevLett.122.054501
[8]
RIOBOO R, TROPEA C, MARENGO M. Outcomes from a drop impact on solid surfaces[J]. Atomization and Sprays, 2001, 11(2): 155-167.
[9]
JOSSERAND C, THORODDSEN S T. Drop impact on a solid surface[J]. Annual Review of Fluid Mechanics, 2016, 48: 365-391. DOI:10.1146/annurev-fluid-122414-034401
[10]
ANTONIO L N, MOREIRA A S, MOITA M R. Advances and challenges in explaining fuel spray impingement: how much of single droplet impact research is useful?[J]. Progress in Energy and Combustion Science, 2010, 36(5): 554-580. DOI:10.1016/j.pecs.2010.01.002
[11]
LIU X, ZHANG X, MIN J C. Maximum spreading of droplets impacting spherical surfaces[J]. Physics of Fluids, 2019, 31(9): 092102. DOI:10.1063/1.5117278
[12]
CHEN M J, WU D, CHEN D Q, et al. Experimental investigation on the movement of triple-phase contact line during a droplet impacting on horizontal and inclined surface[J]. Chemical Engineering Science, 2020, 226: 115864. DOI:10.1016/j.ces.2020.115864
[13]
TABBARA H, GU S. Modelling of impingement phenomena for molten metallic droplets with low to high velocities[J]. International Journal of Heat and Mass Transfer, 2012, 55(7/8): 2081-2086.
[14]
QIN M X, GUO Y, TANG C L, et al. Spreading and bouncing of liquid alkane droplets upon impacting on a heated surface[J]. International Journal of Heat and Mass Transfer, 2020, 159(12): 120076.
[15]
ZHU Y, LIU H R, MU K, et al. Dynamics of drop impact onto a solid sphere: spreading and retraction[J]. Journal of Fluid Mechanics, 2017, 824: R-1-R3-11. DOI:10.1017/jfm.2017.405
[16]
HAO J G. Effect of surface roughness on droplet splashing[J]. Physics of Fluids, 2017, 29(12): 122105. DOI:10.1063/1.5005990
[17]
ŠIKALO Š, TROPEA C, GANIĆ E N. Impact of droplets onto inclined surfaces[J]. Journal of Colloid and Interface Science, 2005, 286(2): 661-669. DOI:10.1016/j.jcis.2005.01.050
[18]
ŠIKALO Š, TROPEA C, GANIĆ E N. Dynamic wetting angle of a spreading droplet[J]. Experimental Thermal and Fluid Science, 2005, 29(7): 795-802. DOI:10.1016/j.expthermflusci.2005.03.006
[19]
ŠIKALO Š, MARENGO M, TROPEA C, et al. Analysis of impact of droplets on horizontal surfaces[J]. Experimental Thermal and Fluid Science, 2002, 25(7): 503-510. DOI:10.1016/S0894-1777(01)00109-1
[20]
RIOBOO R, MARENGO M, TROPEA C. Time evolution of liquid drop impact onto solid, dry surfaces[J]. Experiments in Fluids, 2002, 33: 112-124. DOI:10.1007/s00348-002-0431-x