|
|
|
发布时间: 2022-12-25 |
新能源利用 |
|
|
|
谢飞 |
收稿日期: 2022-04-02
中图法分类号: TK514
文献标识码: A
文章编号: 2096-8299(2022)06-0605-05
|
摘要
基于TracePro光路分析软件, 对菲涅尔反射聚光系统进行了模拟, 发现反射聚光后在光伏电池上的光强分布均匀。在不同追踪精度的情况下, 接收器上接收的能量分析表明追踪精度在±3°以内时, 可以将辐射能量的70%聚集到接收器上。采用主动追踪算法定位太阳位置, 考虑赤经因素对追踪精度的影响, 修正算法后追踪误差小于1°。太阳能电-热综合利用CPV/T系统有效解决了聚光后电池升温的问题, 验证了菲涅尔反射聚光电-热综合利用的可行性。
关键词
太阳能; CPV/T系统; 菲涅尔反射聚光; 单轴追踪
XIE Fei Abstract
Fresnel reflection concentrating system light intensity on photovoltaic cell is evenly distributed, which based on TracePro simulation analysis.The solar energy received after focusing with different tracking accuracy shows that 70% of the radiation energy can be concentrated on the receiver when the tracking accuracy is within ±3°.Consider the influence of right ascension factors, the active solar position algorithm tracking error was less than 1°.CPV/T system can effectively solve the PV cell heating rising after solar concentration, proved the feasibility of Fresnel reflector concentration hybrid Photovoltaic -Thermal system.
Key words
solar energy; CPV/T system; Fresnel reflector; single-axis tracking
实现2030年碳达峰、2060年碳中和的“双碳”目标, 减少化石能源的使用, 建立绿色环保的可再生能源体系迫在眉睫。在这一时代背景下, 太阳能作为一种持续稳定的可再生能源, 最终将会替代传统能源, 成为社会发展的动力源[1]。太阳能发电、集热是目前对于太阳能利用的主要形式, 相同能量的电能和热能, 因为品质因数的不同, 其价值也不同[2]。电能传输和存储方便, 转化成其他形式能量时转换效率高, 因此在太阳能综合利用过程中, 光伏发电是首选, 集热作为补充。合理匹配电能和热能的输出, 实现价值的最大化, 是太阳能电-热综合利用系统研究的重要方向[3]。
聚光是提高单位面积辐照强度最有效的方法。它需要通过光学聚焦和追踪控制来实现[4]。聚光从形式上可分为点聚焦和线聚焦两类, 从原理上可分为菲涅尔聚光和抛物面反射聚光两类[5]。追踪算法则通过建立日地运动模型, 将太阳位置用表达式表示出来。随着考虑因素的增加, 太阳位置算法的复杂程度也相应增加。从实用性的角度考虑, 在满足追踪精度要求的同时, 算法易于编程、减少运算量就显得非常重要[6]。
聚光在提高辐照量的同时会造成电池温度上升, 影响光伏电池的转换效率。研究表明, 温度每上升1 K, 单晶硅、多晶硅电池的效率会降低约0.4%[7]。太阳能聚光的电-热综合利用系统CPV/T是一种互补的解决方案, 不但可以提高光伏效率, 而且还可以附带生产热能, 提高太阳能的电-热综合利用率, 在理论研究和实验中都取得了良好效果[8]。
1 菲涅尔反射聚光分析
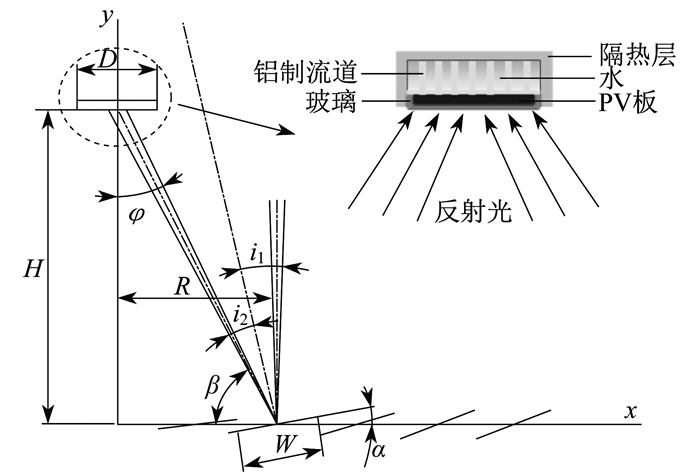
相对于透镜聚光, 菲涅尔反射聚光成本低, 结构简单, 对环境要求低[9]。菲涅尔反射聚光系统设计原理如图 1所示。
图 1中: H为高度; R为每块反射镜到原点的距离; α为反射镜与x轴的夹角; β为反射光与x轴的夹角; φ为反射光与y轴的夹角; i1为入射角; i2为反射角; D为聚光接收器宽度; W为反射镜宽度。通过多组反射面将太阳光汇聚到光伏组件接收器上, 反射聚光的光路几何关系为
| $ 2 \alpha=\varphi=\tan ^{-1} \frac{R}{H} $ | (1) |
确定了H和R后, 就可以确定每块反射镜的倾角α为
| $ \alpha=\frac{1}{2} \tan ^{-1} \frac{R}{H} $ | (2) |
聚光接收器宽度D=160 mm, 高度H=1 955 mm, 反射面两边对称布置, 然后根据R就可以计算出反光板夹角α。菲涅尔反射聚光片的位置参数如表 1所示。
表 1
菲涅尔反射聚光片的位置参数
| R/mm | H/mm | α/(°) |
| 250 | 1 955 | 3.644 |
| 410 | 1 955 | 5.922 |
| 570 | 1 955 | 8.127 |
| 730 | 1 955 | 10.238 |
| 890 | 1 955 | 12.239 |
2 主动追踪算法
2.1 太阳位置算法
对太阳位置的追踪分为两类: 一类通过传感器被动检测辐照量追踪太阳位置, 适用于对精度要求不高的非聚光系统; 另一类则通过建立精确的数学模型, 根据经纬度和时间推导出太阳的具体位置[10]。
2.2 太阳的黄道经度
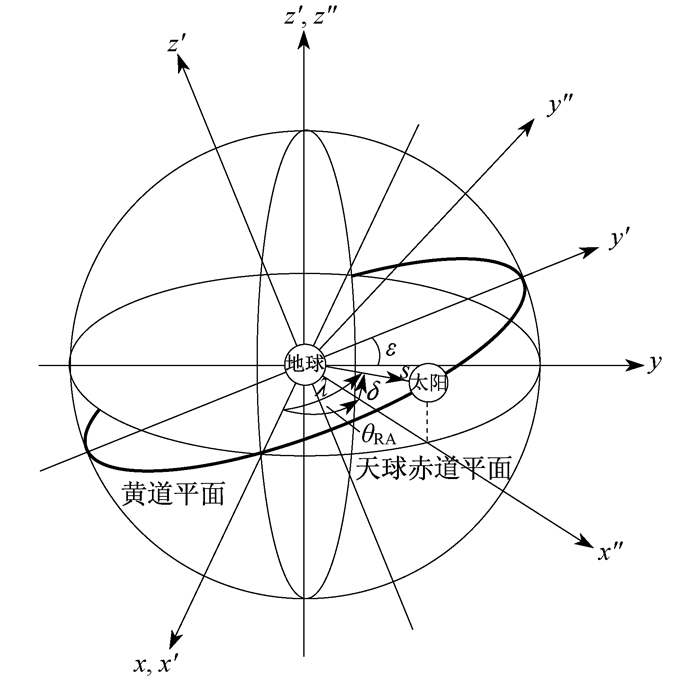
地球公转的平面为黄道平面, 地球自转的平面为赤道平面[11]。以地球为中心建立一个天球体, 如图 2所示。
以地心为坐标系原点, 建立黄道空间坐标系(x′, y′, z′)和赤道空间坐标系(x, y, z)。其中: 黄道平面和赤道平面相较于x(x′)轴, 两平面夹角ε≈23.45°。在黄道空间坐标系(x′, y′, z′)中, 日地运动变成太阳绕地球逆时针旋转。当太阳位于x′轴上时, 就是一年中的冬至(或夏至)。太阳方向S与赤道平面的夹角为赤纬δ, 黄道经度λ是由地心指向太阳的方向向量S与x′轴的夹角。θRA为赤道经度, 用来描述太阳所转过的角度。
λ的表达式为
| $ \begin{gathered} \sin \lambda=\sin \left[360^{\circ} \times \frac{284+n}{365.25}\right] \\ \left(0^{\circ} \leqslant \lambda<360^{\circ}\right) \end{gathered} $ | (3) |
式中: n——一年中的第几天。
2.3 太阳的赤纬
在赤道空间坐标系(x, y, z)中, δ的表达式为
| $ \sin \delta=\sin \lambda \sin \varepsilon $ | (4) |
2.4 时角
时角ω为地球每天自转过的角度。当本地时间正午时ω=0°, 表达式为
| $ \omega=15^{\circ}\left(T_{\mathrm{L}}-12\right) $ | (5) |
式中: TL——以小时计时的本地时间。
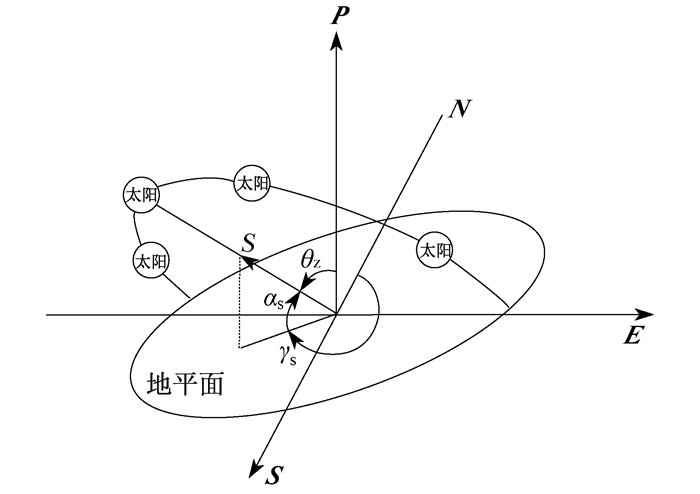
2.5 太阳的高度角
以观测者为原点, 建立地平面坐标系(S, E, P), 其中P轴垂直于地平面, E轴为东方, S轴为南方, 太阳在地平面坐标系中的位置如图 3所示。
图 3中: αS为S与地平面的夹角; γS为S在地平面上的投影与正北N的夹角; Qz为太阳方向法平面与水平面的夹角。αS的表达式为
| $ \begin{gathered} \alpha_{\mathrm{S}}=\sin ^{-1}(\cos \delta \cos \phi \cos \omega+ \\ \sin \delta \sin \phi) \end{gathered} $ | (6) |
式中: ϕ——观测点的纬度。
2.6 太阳的方位角
在地平面坐标系(S, E, P)中, γS的表达式为
| $ \gamma_{\mathrm{S}}=\tan ^{-1}\left(\frac{\sin \omega}{\sin \phi \cos \omega-\tan \delta \cos \phi}\right) $ | (7) |
2.7 儒略日计时
儒略日(Julian Day, JD)中的小数部分表示当天的时间JD(t)。tyy为年, tmm为月, tdd为日, th为格林尼治时(北京时间th-8), tm为分钟, ts为秒。儒略日划分天是从正午12点开始的。2000年1月1日12点的儒略日数JDN为2 451 545。为了简化计算, 将2000年1月1日作为计算的起始时间。根据太阳位置算法, 给出的儒略日JD的表达式[12]为
| $ \begin{aligned} & J_{\mathrm{DN}}= \\ & \text { round }\left[\frac{1\;461 \times\left(t_{\mathrm{yy}}+4\;800+\frac{t_{\mathrm{mm}}-14}{12}\right)}{4}+367-\right. \\ & \left.\frac{3 \times\left(t_{\mathrm{yy}}+4\;900+\frac{t_{\mathrm{mm}}-14}{12}\right)}{400}+t_{\mathrm{dd}}-32\;075\right] \end{aligned} $ | (8) |
| $ J_{\mathrm{D}}=J_{\mathrm{DN}}+\frac{t_{\mathrm{h}}-12}{24}+\frac{t_{\mathrm{m}}}{1\;440}+\frac{t_{\mathrm{s}}}{86\;400} $ | (9) |
| $ J_{\mathrm{D}}(t)=J_{\mathrm{D}}-J_{\mathrm{DN}} $ | (10) |
2.8 考虑赤经影响修正
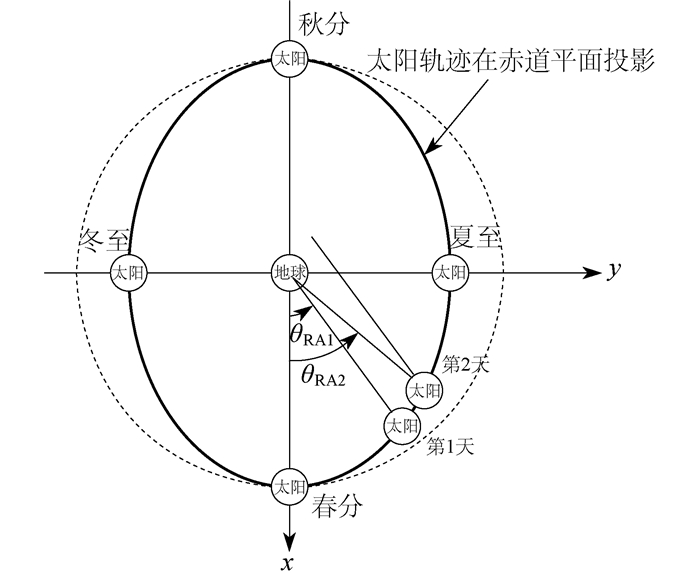
地球绕太阳转动的过程中, 不考虑公转的因素, 通常认为一天为24 h, 地球自转一圈360°。但如果考虑绕太阳的公转, 地球表面观测点太阳到达相同的高度角, 地球实际转动的角度就超过了360°。这就是赤经对太阳位置的影响[13], 如图 4所示, 每天要多转(θRA2-θRA1)的角度。
地球表面任意位置的时角ω关于儒略日时间JD(t)的表达式为
| $ \omega=\frac{\left(J_{\mathrm{D}}(t) \times 360^{\circ}+L_{\text {LOCAL }}\right) {\rm{ \mathsf{ π} }}}{180^{\circ}} $ | (11) |
式中: LLOCAL——经度。
时角ω的取值范围为[0, 2π]。将时角ω和纬度ϕ代入式(6)和式(7)就可以得到本地太阳高度角αS和方位角γS的表达式, 分别为
| $ \alpha_{\mathrm{S}}=\sin ^{-1}\left(\cos \delta \cos \phi \cos \omega+\cos \delta \sin 2 \theta_{\mathrm{RA}} \cos \phi \sin \omega+\sin \delta \sin \phi\right) $ | (12) |
| $ \gamma_{\mathrm{S}}=\tan ^{-1}\left(\frac{\sin \omega-\sin 2 \theta_{\mathrm{RA}} \cos \omega}{\sin \phi \cos \omega+\sin 2 \theta_{\mathrm{RA}} \sin \phi \sin \omega-\tan \delta \cos \phi}\right) $ | (13) |
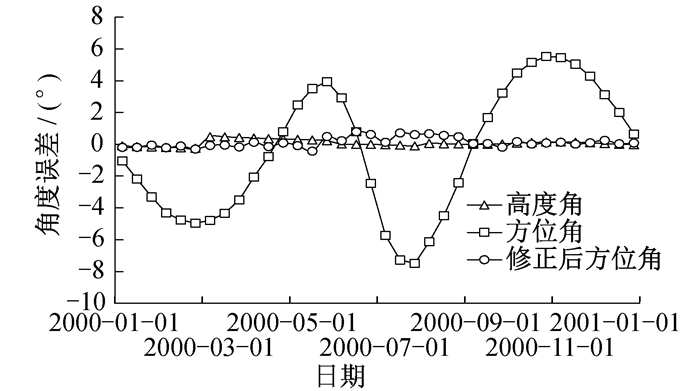
由于受地球轨道的偏心率和黄赤夹角的影响, 每日太阳方位角为180°时, 并不是观测点本地标准时间的12点, 全年前后误差约为±15 min。如果按照标准时间确定方位角, 最大会产生8°的角度误差。引入赤经因素影响修正算法后, 方位角每日误差小于1°, 满足低倍聚光对追踪算法精度的要求。考虑赤经修正后方位角误差对比如图 5所示。
3 结果分析
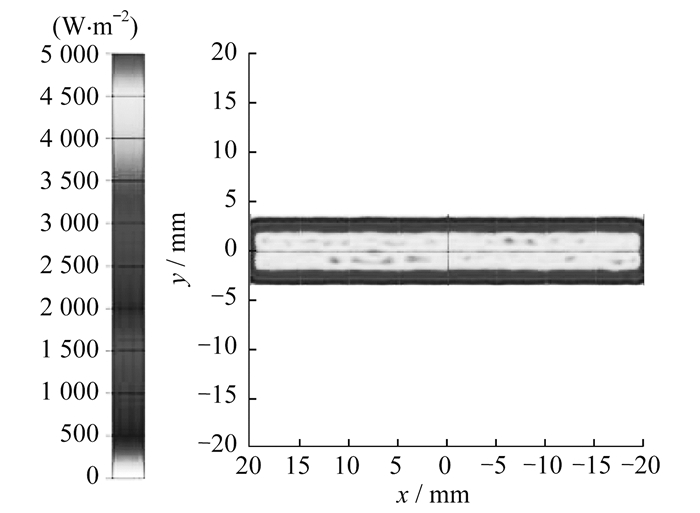
使用TracePro对菲涅尔反射聚光后聚光器上的光强分布进行模拟分析, 结果如图 6所示。
由图 6可知: 在接收器区域光强分布均匀; 辐照度最小值为4.824 6×10-16 W/m2, 最大值为4 806.5 W/m2, 平均值为3 671.9 W/m2, 均方值为1 351.3 W/m2, 总光通量为0.881 25 W; 入射光线为148 104条。
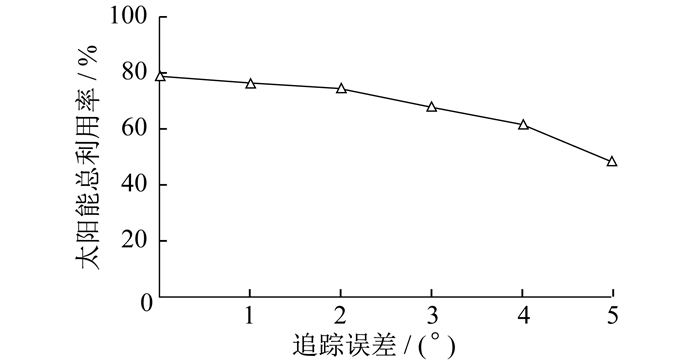
考虑到追踪过程存在的误差, 针对出现1°~5°的追踪误差接收器能量的变化进行分析。当追踪精度误差大于3°时光学损失>30%, 所以菲涅尔反射聚光系统的追踪精度应控制在±3°内, 以便聚光系统总的利用率大于70%。菲涅尔反射聚光追踪误差对太阳能总利用率的影响如图 7所示。
选取一日的试验数据, 横坐标为时间, 纵坐标左侧为功率, 右侧为温度, 将菲涅尔反射聚光与非聚光进行对比, 实验结果如图 8所示。图 8中: 曲线1为太阳直接辐射时光伏输出的最大功率; 曲线2为10倍聚光后光伏输出的最大功率; 曲线3是未聚光时接收器(即电池)的温度; 曲线4是10倍聚光后接收器上的温度。
由图 8可以看出, 当天气晴朗、无云层时, 聚光可以明显提高光伏电池的发电功率; 当云层遮挡太阳后, 聚光和非聚光发电效率相当, 体现不出聚光的优势。由此表明, 菲涅尔反射聚光系统在提高常规光伏电池输出功率的同时, 可以获得一定的热能, 可以实现太阳能电-热综合利用。
在菲涅尔反射聚光实验过程中, 采用热成像仪对接收器进行拍摄测量。实验在同一日不同辐照度的情况下进行, 组件温度分布情况如图 9所示, 最高温度点在37~132 ℃之间。
由图 9可以看出, 光伏组件的温度分布均匀, 没有出现局部过热的现象。
4 结论
通过模拟分析和实验, 得到如下结论。
(1) 菲涅尔反射聚光的CPV/T系统在提高光伏电池上辐照度的同时, 不会产生能量集中的区域, 避免了因电池板的局部高温影响光伏转换效率、损坏电池的情况。
(2) 对太阳位置的主动追踪算法进行分析推导, 修正赤经因素引起的方位角算法中误差, 使得追踪算法精度误差小于1°。
(3) 电池板背部的冷却系统起到冷却电池、收集热能的作用, 提高了太阳能电-热综合利用的转换效率。
(4) 对10倍反射聚光与直接辐射的光伏发电系统进行对比实验可知, CPV/T系统可以有效提高电能输出, 同时避免聚光后光伏电池温度升高造成的效率下降, 将冷却过程中产生的热能进行回收, 实现了提高太阳能综合利用率的目的。
参考文献
-
[1]姚博伟, 张涛, 朱群志. 太阳能热水系统及光伏光热系统在上海地区年运行性能研究[J]. 上海电力学院学报, 2017, 33(2): 107-112. DOI:10.3969/j.issn.1006-4729.2017.02.001
-
[2]YAZDANIFARD F, AMERI M. Exergetic advancement of photovoltaic/thermal systems (PV/T): a review[J]. Renewable and Sustainable Energy Reviews, 2018, 97: 529-553. DOI:10.1016/j.rser.2018.08.053
-
[3]REN S, FENG X, YANG M. Cumulative solar exergy allocation in heat and electricity cogeneration systems[J]. Energy, 2022, 254: 124464. DOI:10.1016/j.energy.2022.124464
-
[4]SULTAN S M, EFZAN M N E. Review on recent photovoltaic/thermal (PV/T) technology advances and applications[J]. Solar Energy, 2018, 173: 939-954. DOI:10.1016/j.solener.2018.08.032
-
[5]WANG G, WANG F, SHEN F, et al. Experimental and optical performances of a solar CPV device using a linear Fresnel reflector concentrator[J]. Renewable Energy, 2020, 146: 2351-2361. DOI:10.1016/j.renene.2019.08.090
-
[6]朱永强, 刘家豪, 杨晓华, 等. 一种新型单轴太阳跟踪方式[J]. 太阳能学报, 2021, 42(3): 347-352.
-
[7]韩林岑, 朱群志. 基于相变材料的太阳能电池板温度控制实验研究[J]. 上海电力学院学报, 2019, 35(4): 391-394.
-
[8]SINGH R, KUMAR S, GEHLOT A, et al. An imperative role of sun trackers in photovoltaic technology: a review[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 3263-3278. DOI:10.1016/j.rser.2017.10.018
-
[9]LIU Y, HU P, ZHANG Q, et al. Thermodynamic and optical analysis for a CPV/T hybrid system with beam splitter and fully tracked linear Fresnel reflector concentrator utilizing sloped panels[J]. Solar Energy, 2014, 103: 191-199. DOI:10.1016/j.solener.2014.01.047
-
[10]HOADLEY D. Efficient calculation of solar position using rectangular coordinates[J]. Solar Energy, 2021, 220: 80-87. DOI:10.1016/j.solener.2021.02.019
-
[11]GRENA R. An algorithm for the computation of the solar position[J]. Solar Energy, 2008, 82(5): 462-470. DOI:10.1016/j.solener.2007.10.001
-
[12]REDA I, ANDREAS A. Solar position algorithm for solar radiation applications[J]. Solar Energy, 2004, 76(5): 577-589. DOI:10.1016/j.solener.2003.12.003
-
[13]ZHANG T, STACKHOUSE P W, MACPHERSON B, et al. A solar azimuth formula that renders circumstantial treatment unnecessary without compromising mathematical rigor: mathematical setup, application and extension of a formula based on the subsolar point and atan2 function[J]. Renewable Energy, 2021, 172: 1333-1340. DOI:10.1016/j.renene.2021.03.047
