|
|
|
发布时间: 2022-12-25 |
新能源利用 |
|
|
|
收稿日期: 2022-04-02
中图法分类号: TK01+9
文献标识码: A
文章编号: 2096-8299(2022)06-0610-07
|
摘要
针对太阳能光伏制冷系统使用过程存在的供需不匹配现象, 充分利用建筑本身的热惰性和蓄热属性, 展开基于建筑虚拟储能的供需匹配性研究。首先, 基于DeST建立了上海地区典型办公建筑, 在完成可靠性验证的基础上, 设计了太阳能光伏制冷系统并预测了典型日光伏阵列的逐时发电量。然后, 确定了虚拟储能的充放时间和对建筑负荷的消减情况, 并基于虚拟储能技术对制冷机电耗进行了优化, 采用本址供能满足负荷占比(OEF)以及本址供能满足自消费占比(OEM)2个评价指标对系统供需匹配进行评价。结果表明: 采用虚拟储能后, 系统OEF从75.76%提升到86.54%, OEM从75.73%提升到91.05%, 当日最大余量电量消减幅度可达54.81%。
关键词
太阳能光伏制冷系统; 能耗模拟; 光伏预测; 虚拟储能; 供需匹配性
Abstract
Aiming at the mismatch between supply and demand in the use of solar photovoltaic refrigeration systems, this paper makes full use of the thermal inertia and heat storage properties of the building itself, and conducts a research on the matching of supply and demand based on building virtual energy storage.Firstly, a typical office building in Shanghai was established based on DeST.After completing the reliability verification, the solar photovoltaic cooling system was designed and the hourly power generation of the photovoltaic array was predicted.After that, the charging and discharging time of virtual energy storage and the reduction of building load were determined, and the power consumption of refrigerators was optimized based on virtual energy storage technology.The energy supply of this site meets the self-consumption ratio (On-site energy matching, OEM) two evaluation indicators to evaluate the supply and demand matching of the system.The results show that after using virtual energy storage: system OEF=86.54%, OEM=91.05%, while the original The system OEF=75.76%, OEM=75.73%, the maximum remaining power reduction on the day can reach 54.81%.
Key words
solar photovoltaic cooling system; energy consumption simulation; photovoltaic forecasting; virtual energy storage; supply and demand matching
我国能源总体消耗量巨大, 在电力需求不断增大的情况下, 开发太阳能等新能源代替传统能源, 对于降低我国能源消耗, 维持社会的持续发展意义重大。太阳能光伏制冷技术利用光伏装置将太阳能转化为电能, 再以电能驱动设备进行制冷[1-2], 但由于太阳能的不确定性, 导致供需侧存在不匹配现象。储能技术可以实现能量的跨时段转移从而可有效解决供需不匹配问题, 但其造价较高不利于系统的经济性。建筑虚拟储能利用建筑的蓄热属性和热惰性, 可以对需求侧能源进行优化管理与调节, 通过一定的控制策略实现建筑对能源的存储或者释放, 因此在太阳能波动较大的情况下, 合理利用虚拟储能可以发挥类似传统储能的作用[3-4]。目前, 针对虚拟储能的研究已有部分成果。童亦斌等人[5]分析了虚拟储能的主要影响因素, 建立了虚拟储能能量功率模型, 并根据实际测算结果表明空调负荷可以参与电网调节。王怡岚等人[6]根据热力学模型和人体舒适度模型建立了虚拟储能模型, 以实际空调建筑为算例分析了虚拟储能的性能。赵军等人[7]采用虚拟储能主动调控建筑的热负荷, 从而提高了太阳能供热量和建筑负荷的匹配程度。靳小龙等人[8]基于楼宇蓄热建立了建筑虚拟储能模型并融合到分布式能源优化调度模型当中, 通过优化调度的对比分析, 表明了虚拟储能的参与使系统经济性更优。为进一步认识建筑虚拟储能的应用价值, 本文以上海地区办公建筑为研究对象, 设计太阳能光伏制冷系统, 针对系统存在的供需不匹配问题, 基于建筑虚拟储能展开供需匹配性研究。具体工作为: 建立了上海地区标准的办公建筑, 基于DeST软件平台完成了典型年能耗模拟并结合已有研究结果表明了所建模型的可靠性; 为所建办公建筑设计了一套太阳能光伏制冷系统, 建立了光伏预测模型并在典型日预测了当天的逐时发电量; 针对系统的供需不匹配问题, 展开基于建筑虚拟储能的供需匹配性研究, 模拟过程确定了当天建筑虚拟储能对建筑负荷的额定消减电量以及释能时间的估算, 并利用建筑虚拟储能技术使典型日系统供需匹配性大幅度提高。
1 典型办公建筑建模及可靠性验证
1.1 典型办公建筑建模
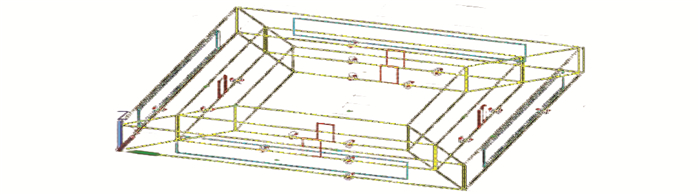
基于DeST设计上海地区方形办公建筑。该建筑长40 m, 宽40 m, 每层高4 m, 高3层, 总建筑面积4 800 m2。其标准层分为中心核心系统区域和核心系统外围的办公空间, 东西南北4个方向各有一个内区和一个外区, 外区的进深为5 m。其中: 核心系统区域为非空调区域, 该区域主要承担洗手间、楼梯、开水间等功能, 单层面积为400 m2, 占总面积的25%;4个方向内外区都为空调区, 占总面积的75%;建筑的朝向为正南方向。其典型代表层三维立体图如图 1所示。
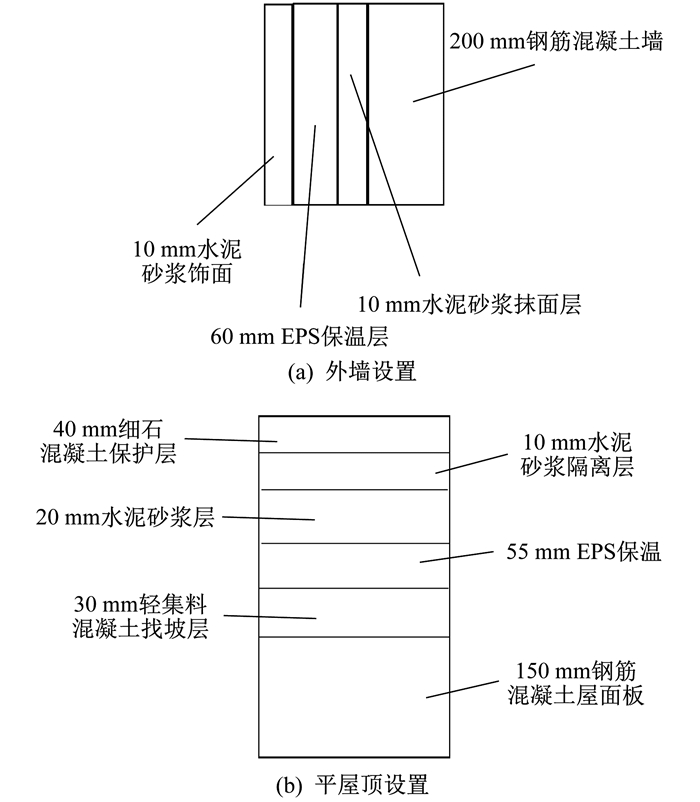
为使建筑材料物性参数、结构、空调系统等设置符合实际情况, 主要参考《公共建筑节能设计标准》《民用建筑热工设计规范》《绿色建筑节能设计规范》《外墙外保温建筑构造》《平屋面设计构造》等规范与标准。外墙及平屋顶结构构造最终结果及材料物性参数的设置分别如图 2和表 1所示。
表 1
材料物性参数
| 物性参数 | 导热系数/[W·(m·K)-1] | 密度/(kg·m-3) | 蓄热系数/[W·(m2·K)-1] |
| 水泥砂浆 | 0.930 | 1 800 | 11.373 |
| EPS保温板 | 0.039 | 30 | 0.360 |
| 钢筋混凝土 | 1.740 | 2 500 | 17.204 |
| 细石混凝土 | 1.740 | 2 300 | 17.204 |
| 轻集混凝土 | 0.450 | 1 000 | 7.502 |
建筑东、西、南、北4个方向的窗墙比为0.45, 窗户的传热系数为2.4 W/(m2·K), 太阳得热系数取值0.348, 遮阳系数取值0.4。参考《公共建筑节能设计标准》的推荐值, 设置的人员、灯光热扰、设备热扰、通风次数如表 2所示。
表 2
人员、灯光、设备及通风次数设置情况
| 人员/(m2·人-1) | 灯光热扰/(W·m-2) | 设备热扰/(W·m-2) | 通风次数/(次·h-1) |
| 8 | 9 | 15 | 0.7 |
空调系统选择风机盘管加新风系统, 设置房间温度夏季上限为26 ℃, 冬季下限为20 ℃。系统送风温度上下限分别设置为18°和30°。冷源系统使用的冷机选择内置的螺杆式制冷机, 其额定制冷系数(Coefficient Of Perfermance, COP)为5.85。热源系统中热源为燃气锅炉, 采用两管制水系统, 供水温度夏季为7°, 冬季为60°。设定全年双休日和法定节假日空调处于关闭状态。
1.2 模拟结果分析与验证
图 3显示了上海地区办公建筑典型年能耗模拟情况。
已有文献表明[9-10], 上海地区大型办公建筑单位面积能耗水平在37.6~234.1 kWh/(m2·a), 统计平均值为114.0 kWh/(m2·a)。本文研究结果将燃气消耗折算为电耗, 最终结果表明建筑的单位面积能耗为100.53 kWh/(m2·a), 接近统计平均值。各分项能耗运行参考指标, 空调系统能耗占比40% ~60%, 本次模拟结果为38%;照明能耗占比13% ~26%, 一般为20% 左右, 本次模拟结果为19%;办公设备能耗为20% ~40%, 本次模拟结果为25%。因此, 所建典型办公建筑及相关参数的设置比较合理, 具有一定的可靠性。
2 太阳能光伏制冷系统的设计与光伏预测
2.1 太阳能光伏制冷系统设计
对所建典型办公建筑设计太阳能光伏制冷系统供应建筑所需冷负荷, 并在建筑屋顶设计一套光伏阵列。该系统结构示意如图 4所示。
其基本工作原理为: 光伏阵列将太阳能转换为电能, 经过逆变器转化为交流电供应制冷机, 系统不足部分电力由电网提供, 光伏阵列为离网形式, 多余电力存储在蓄电池中。
2.2 光伏预测模型建立
光伏组件为获得更优出力需要倾斜放置, 而DeST提供的辐射量为水平面上的辐射量, 因此需要建立倾斜面太阳辐射模型。水平面上太阳总辐射包括: 水平面直射辐射和水平面散射辐射。倾斜面太阳总辐射包括: 倾斜面直射辐射、倾斜面散射辐射、倾斜面反射辐射。水平面到倾斜面辐射量的转换关系的计算模型如下[11]。
直射辐射模型为
| $ \left\{\begin{array}{l} I_{\mathrm{BT}}=I_{\mathrm{BH}} \frac{\cos \theta}{\sin \alpha} \\ \cos \theta=(\sin \delta \cos \beta-\cos \delta \cos \lambda \sin \beta) \sin \sigma+ \\ \quad(\cos \delta \cos \beta+\sin \delta \cos \lambda \sin \beta) \cos \sigma \cos \omega+ \\ \sin \lambda \sin \beta \cos \sigma \sin \omega \\ \sin \alpha=\sin \delta \sin \sigma+\cos \delta \cos \sigma \cos \omega \end{array}\right. $ | (1) |
式中: IBT, IBH——倾斜面、水平面直射辐射;
θ——太阳入射角;
α——太阳高度角;
δ——当地纬度;
β——倾斜面倾角;
λ——倾斜面方位角;
σ——赤纬角;
ω——时角。
散射辐射模型采用工程上常用的Hay模型, 即
| $ \left\{\begin{array}{l} I_{\mathrm{DT}}=\frac{I_{\mathrm{DH}}-I_{\mathrm{BH}}}{I} \cdot \frac{1+\cos \beta}{2}+I_{\mathrm{DH}} \frac{I_{\mathrm{BH}}}{I_0} R_{\mathrm{B}} \\ R_{\mathrm{B}}=\max \left(0, \frac{\cos \theta}{\sin \alpha}\right) \\ I_0=1\;367 \times\left\{1+0.033\left[\frac{{\rm{ \mathsf{ π} }}(N-3)}{365}\right]\right\} \end{array}\right. $ | (2) |
式中: IDT, IDH——倾斜面、水平面散射辐射;
I——水平面散射辐射与大气层的上边界面的太阳辐射量之比;
I0——大气层上边界面的太阳辐射量;
RB——折算因子;
N——天数。
反射辐射模型为
| $ I_{\mathrm{RT}}=\frac{\rho I_{\mathrm{H}}(1-\cos \beta)}{2} $ | (3) |
式中: IRT——倾斜面反射辐射;
IH——水平面上太阳总辐射;
ρ——地面平均反射率, 取0.15。
结合太阳辐射模型, 可以计算得到光伏预测模型[2]为
| $ \left\{\begin{array}{l} \eta_{\mathrm{PV}}=\tau_{\mathrm{PV}} \eta_0\left[1-0.004\;5\left(T_{\mathrm{CELL}}-25\right)\right] \\ \tau_{\mathrm{PV}}=\tau_{\mathrm{PV} 0}\left[1-0.1\left(\frac{1}{\cos \theta_1}-1\right)\right] \\ T_{\mathrm{CELL}}=T_{\mathrm{A}}+0.03 I \\ P_{\mathrm{PV}}=\eta_{\mathrm{I}} \eta_{\mathrm{PV}} I S_{\mathrm{PV}} \end{array}\right. $ | (4) |
式中: ηPV, η0——光伏电池的光电转换效率, 标准测试条件下的光电转换效率;
τPV, τPV0——太阳电池各层透过率和太阳电池辐射入射角为0°时的值, 后者取0.81;
TCELL, TA——光伏电池的温度和环境温度, ℃;
θ1——光伏板平面上的辐射入射角, °;
PPV——光伏组件的发电功率, kW;
ηI——逆变器效率, 取值0.98;
SPV——光伏板的面积, m2。
光伏预测模型里面全天光伏板上的辐射入射角θ1计算公式如下
| $ \cos \theta_1=\sin \sigma \sin \delta+\cos \sigma \cos \delta \cos \omega $ | (5) |
| $ \left\{ {\begin{array}{*{20}{l}} {\sin \sigma = 0.397\;95 \times }\\ {\;\;\;\;\;\;\; \;\;\;\cos \left[ {\frac{{0.985\;63(N - 173)}}{{180{\rm{ \mathsf{ π} }} }}} \right]}\\ {\omega = 15\left( {{T_{\rm{s}}} - 12} \right)} \end{array}} \right. $ | (6) |
式中: Ts——真太阳时。
2.3 光伏组件设计与预测结果
为增强太阳能光伏制冷系统设计的可靠性, 在上海地区办公建筑典型年能耗模拟使用数据基础上, 选择7月份温度最高日(7月20日)的气象数据计算光伏总面积, 以期光伏发电可以尽可能满足制冷季制冷机的耗电量。光伏组件参考隆基乐叶公司型号为LR4-60HPH-380M的组件, 在标准测试条件下组件效率为20.9%, 单块组件长175.5 cm、宽103.8 cm, 根据已有研究结果[12], 选择光伏阵列的朝向为正南, 倾角23°。
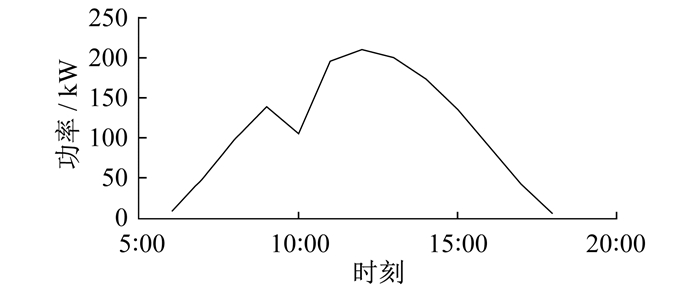
结合DeST提供的干球温度和水平面辐射情况, 可以计算当天光伏阵列逐时发电量。最终计算的典型日单块光伏组件发电量计算结果如图 5所示。
根据光伏组件的全天发电量满足螺杆制冷机当日耗电量的原则, 计算光伏面积, 取整可得需要光伏组件共436块, 则总光伏面积不超过795 m2, 约占建筑屋顶面积的一半。因此, 本文的设计满足光伏阵列的外在条件。
3 基于建筑虚拟储能的供需匹配性研究
3.1 虚拟储能模型及工作原理介绍
虚拟储能可以充分利用建筑的热惰性和蓄热属性, 因此和建筑负荷以及室内温度存在一种相互关系, 合理的利用这种耦合关系, 可以在实际情况中发挥一定的价值。由于涉及热量的传递与室内温度的关系, 因此从热力学基本定律出发, 其基本模型为
| $ \left\{\begin{aligned} C \rho_0 V \frac{\mathrm{d} t}{\mathrm{~d} \tau}= & \sum Q(\tau) \\ \sum Q(\tau)= & Q_{\mathrm{WIN}}(\tau)+Q_{\mathrm{WALL}}(\tau)+Q_{\mathrm{F}}(\tau)+ \\ & Q_{\mathrm{IN}}(\tau)+Q_{\mathrm{SUPPLY}}(\tau) \end{aligned}\right. $ | (7) |
式中: C——室内空气比热容, J/(kg·K);
ρ0——室内空气密度, kg/m3;
V——室内空气体积, m3
t——温度, ℃;
∑Q(τ)——热功率;
QWIN——通过窗的传热, kW;
QWALL——通过围护结构的传热, kW;
QF——室内物体间得传热, kW;
QIN——室内物体和人员等的发热, kW;
QSUPPLY——内部设备的供热, kW。
其工作原理为: 充分利用建筑本身的热惰性和蓄热属性, 在电量充裕时适当降温, 相当于给建筑充能, 在发电量不足时将储存在建筑里的能量释放出来。利用建筑负荷与室内温度的相互关系, 通过室温调控的方法对建筑负荷进行优化调节, 达到类似蓄电池的作用。
3.2 虚拟储能对建筑负荷消减情况及释能时间确定
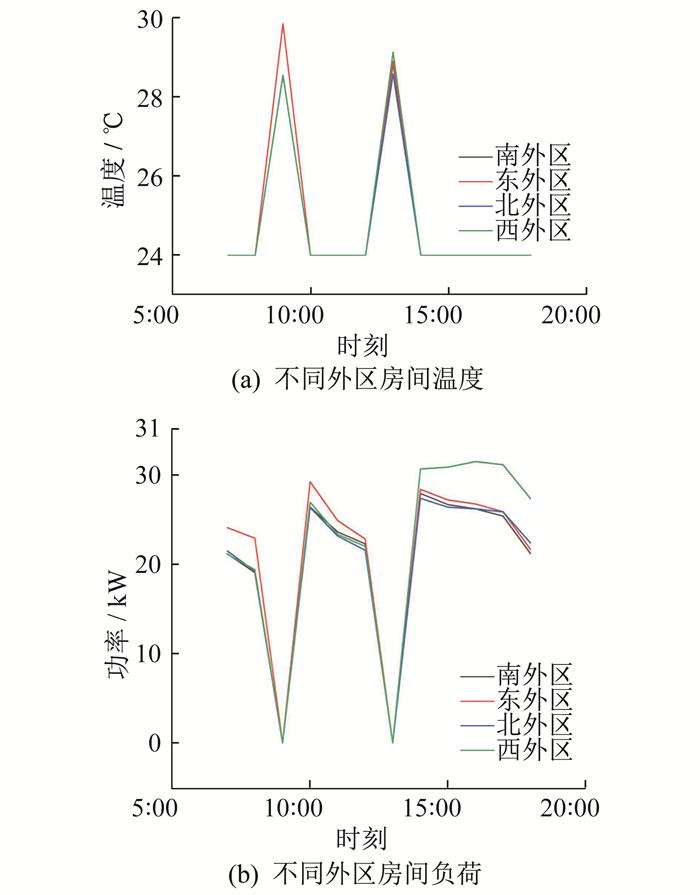
为了解典型日建筑虚拟储能对建筑负荷的最大消减幅度, 以及建筑存储和释放冷量的快慢, 首先要确定建筑房间舒适度区间。其基本思路是: 对建筑进行最大充能, 然后在某时刻关闭所有房间空调, 让建筑存储的冷量不断释放, 释放极限是室内温度达到房间温度上限为止。在本次过程中, 建筑存储冷量导致的房间温度下降, 其温度下限不得低于24 ℃, 由于释放冷量导致的温度上升其温度上线不得高于28 ℃。此段过程即建筑虚拟储能释放冷量的过程, 结果是导致室内温度存在一个缓慢的滞后现象, 使室内温度在一定时间段内仍然保持在舒适度区间。具体操作情况如下: 基于DeST平台, 在上午7时到8时, 将所有房间开启空调, 使室温达到24 ℃, 让建筑完成最大充能; 在上午8时到10时关闭空调, 观察建筑释放冷量过程的快慢以及超出室温舒适度区间的时间点, 通过这种方法可以大致确定建筑在典型日完全释放冷量的时间; 10时到12时打开空调继续对建筑进行充能; 下午时段再重复一次上述过程。
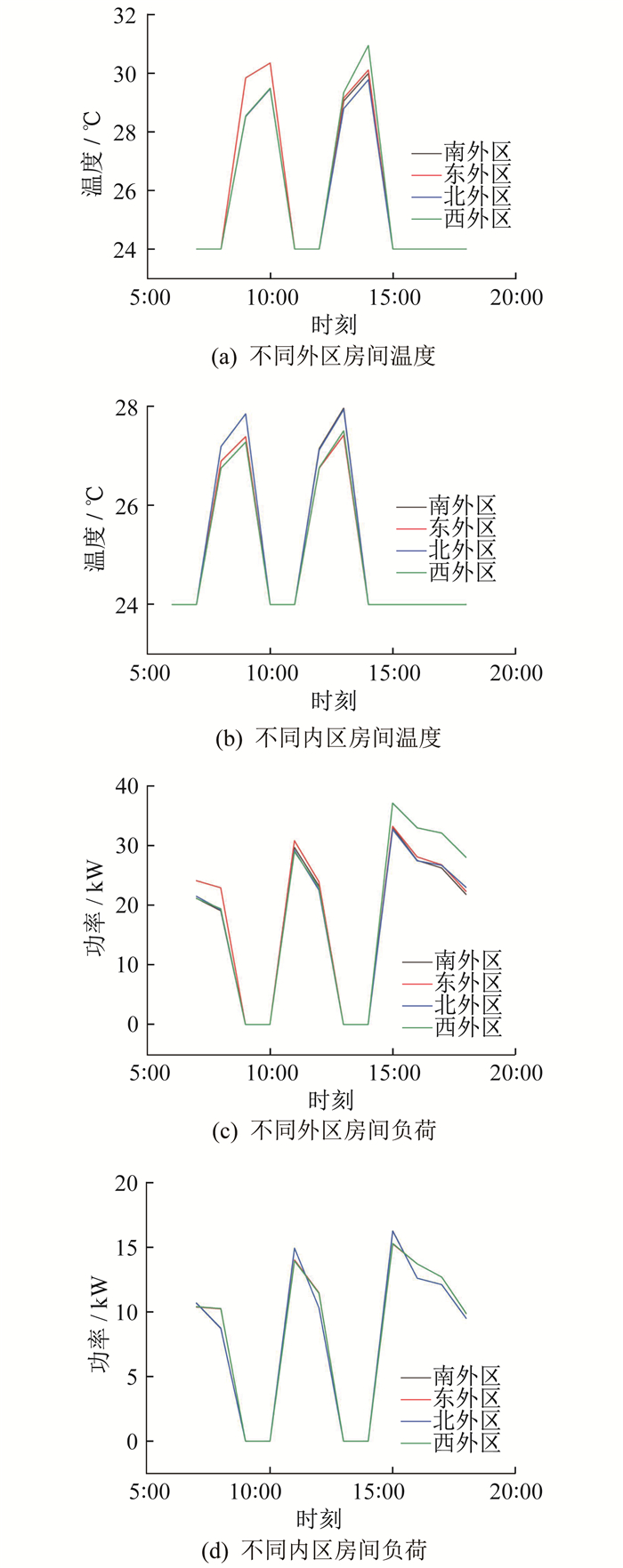
整个过程内外区房间温度和负荷变化情况如图 6所示。对比图 6的两次结果是否差距明显, 如果差距很小, 则说明所得结果具有一定的可靠性。
图 7为空调关闭最大时长为1 h(分别在上午的9时和下午的13时关闭空调)的外区温度和负荷变化情况。
由图 6和图 7可知: 建筑房间由于内外区的区别导致建筑释放冷量的速率存在明显不同, 所以在2 h的时间, 观察温度是否超出舒适度区间。外区温度在1 h后已经超出了温度舒适范围, 而内区温度在2 h后依然在舒适度范围, 并且已经接近释放极限, 故知在该典型日内区完全释能时间最快接近2 h, 外区释能时间最快接近1 h。内区房间基本可以将存储的冷量全部释放出来, 建筑虚拟储能导致内区房间冷量消减幅度最大不超过12 kWh, 系统对内区房间进行充能, 最大接近15 kWh冷量; 外区房间由于释能时间明显快于内区, 在1 h内, 建筑虚拟储能释能使房间冷量消减幅度最大不超过23 kWh, 系统对外区房间进行充能, 最大接近30 kWh冷量。
因此, 在所得结果的基础上估算整栋建筑在1 h内由于虚拟储能的作用使系统消减最大不超过420 kWh冷量, 系统对建筑充能最大接近540 kWh冷量, 如果按制冷机的额定COP折算成电负荷, 则在典型日虚拟储能1 h对系统的额定消减电量接近71.794 9 kWh, 系统对建筑额定充电量最大接近92.307 7 kWh。
3.3 评价指标及供需匹配性研究
为研究太阳能光伏制冷系统的供需匹配性, 选择2个参数对系统供需匹配性进行评价: 本址供能满足负荷占比(On-site energy fraction, OEF), 本址供能满足自消费占比(On-site energy matching, OEM)[13]。其定义式如下
| $ {F_{{\rm{OE}}}} = \frac{{\sum\limits_{i = {\tau _1}}^{{\tau _2}} {\min } (G(i), L(i))}}{{\sum\limits_{i = {\tau _1}}^{{\tau _2}} L (i)\mathit{\Delta }\tau }} $ | (8) |
| $ {M_{{\rm{OE}}}} = \frac{{\sum\limits_{i = {\tau _1}}^{{\tau _2}} {\min } (G(i), L(i))}}{{\sum\limits_{i = {\tau _1}}^{{\tau _2}} G (i)\mathit{\Delta }\tau }} $ | (9) |
式中: FOE, MOE——OEF, OEM的值, 取值范围均为[0, 1];
τ1, τ2——起始时间和终止时间;
G(i)——i时刻本址发电量, kW;
L(i)——i时刻建筑所需负荷, kW;
Δτ——时间步长。
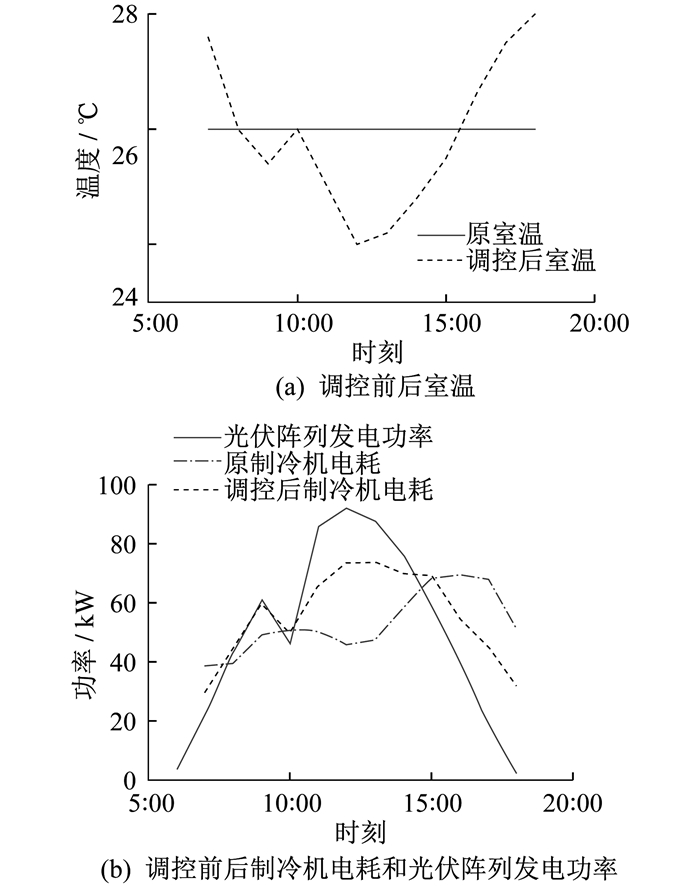
为提高光伏阵列供需匹配性, 充分发挥建筑虚拟储能的使用价值, 本文基于建筑虚拟储能的工作原理调控室内温度, 实现建筑冷负荷的释放, 并最终反应在电力消耗上, 结果如图 8所示。
原系统OEF为75.76%, OEM为75.73%, 最大余量电量为130.462 2 kWh。根据结果计算评价指标, 得到采用虚拟储能后, 系统OEF为86.54%, OEM为91.05%, 当日最大余量电量为58.955 9 kWh, 当日最大余量电量削减幅度达54.81%。
4 结论
本文以上海地区典型办公建筑为研究对象, 基于建筑虚拟储能展开供需匹配性研究, 结果表明了虚拟储能的应用价值, 对于上海地区办公建筑虚拟储能提供了借鉴意义。具体研究结论如下:
(1) 所建办公建筑内外区的释能时间有较大差别, 内区释能时间接近2 h, 而外区释能时间接近1 h。
(2) 典型日虚拟储能在1 h内对系统的额定消减电量接近71.794 9 kWh, 系统对建筑额定充电量最大接近92.307 7 kWh。
(3) 为提高系统的供需匹配性, 采用虚拟储能技术对建筑进行合理充放电进而优化系统电耗曲线, 使评价指标OEF从75.76% 提升到86.54%, OEM从75.73% 提升到91.05%, 并且当日最大余量电量削减幅度可达54.81%。这对于降低蓄电池的初始投资意义重大。
参考文献
-
[1]段芮. 太阳能制冷技术的特点与现状[J]. 上海电力学院学报, 2009, 25(1): 75-78. DOI:10.3969/j.issn.1006-4729.2009.01.019
-
[2]高毓壑, 季杰, 赵志, 等. 太阳能光伏制冷系统与其他制冷系统的能耗模拟及经济性比较[J]. 太阳能学报, 2020, 41(5): 336-344.
-
[3]GUELPA E, VERDA V. Optimization of the thermal load profile in district heating networks through "virtual storage" at building level[J]. Energy Procedia, 2016, 101: 798-805. DOI:10.1016/j.egypro.2016.11.101
-
[4]CHENG M, SAMI S S, WU J. Benefits of using virtual energy storage system for power system frequency response[J]. Applied Energy, 2017, 194: 376-385. DOI:10.1016/j.apenergy.2016.06.113
-
[5]童亦斌, 游小杰, 王怡岚, 等. 空调负荷虚拟储能技术研究[J]. 北京交通大学学报, 2017, 41(5): 126-131.
-
[6]王怡岚, 童亦斌, 黄梅, 等. 基于需求侧响应的空调负荷虚拟储能模型研究[J]. 电网技术, 2017, 41(2): 394-401.
-
[7]赵军, 金玉, 李浩, 等. 基于虚拟储能的建筑可再生能源系统设计与优化[J]. 太阳能学报, 2021, 42(5): 91-97.
-
[8]靳小龙, 穆云飞, 贾宏杰, 等. 融合需求侧虚拟储能系统的冷热电联供楼宇微网优化调度方法[J]. 中国电机工程学报, 2017, 37(2): 581-591.
-
[9]徐强. 上海市大型公共建筑能耗统计分析[C]//中国城市科学研究会. 城市发展研究——第7届国际绿色建筑与建筑节能大会论文集. 北京: 《城市发展研究》编辑部, 2011: 330-334.
-
[10]朱伟峰, 蒋友娣. 上海大型公共建筑分项运行能耗参考指标研究[J]. 暖通空调, 2013, 43(11): 3-7.
-
[11]吴贞龙, 徐政, 胡晓燕, 等. 倾斜面太阳辐照度实用计算模型的研究[J]. 太阳能学报, 2016, 37(3): 787-793.
-
[12]胡一东, 谭洪卫. 上海地区绿色建筑中光伏系统应用分析[J]. 建筑节能, 2017, 45(2): 39-45.
-
[13]康利改. 分布式冷热电联供系统动态匹配的弱解耦优化研究[D]. 天津: 天津大学, 2017.