|
|
|
发布时间: 2023-04-28 |
综合能源管理 |
|
|
|
收稿日期: 2022-04-02
基金项目: 国家电网有限公司科技项目(5100-202117568A-0-5-SF)
中图法分类号: TK01+9
文献标识码: A
文章编号: 2096-8299(2023)02-0149-09
|
摘要
零碳能源系统是建设清洁低碳能源体系、促进碳中和目标达成的有效途径。但风、光等可再生能源发电的间歇性和波动性给零碳能源系统的合理规划与科学配置带来巨大挑战。基于此,提出了基于长短期记忆网络(LSTM)分位数回归的零碳能源系统不确定性规划方法。首先,构建了零碳能源系统的物理结构,并对系统内典型设备进行建模;其次,基于区间数理论思想,构建了基于LSTM分位数回归的光伏发电区间预测模型;然后,以系统年总经济成本最小为目标函数,构建了可实现设备配置与运行策略协同优化的混合整数线性规划模型;最后,通过典型算例分析,验证了所提模型应对零碳能源系统不确定性规划的可行性。
关键词
零碳能源系统; 不确定性; LSTM分位数回归; 优化规划
Abstract
Zero-carbon energy system is an effective way to promote the construction of clean and low-carbon energy system and realize carbon neutralization.However, the intermittence and volatility of wind, solar and other renewable energy power generation have brought great challenges to the rational planning and scientific allocation of zero-carbon energy system.In this paper, an uncertainty programming method for zero-carbon energy system based on LSTM quantile regression is proposed.Firstly, the physical structure of the zero-carbon energy system is constructed, and the typical equipment in the system is modeled.Then, based on the interval number theory, the interval prediction model of photovoltaic power generation based on LSTM quantile regression is constructed.Taking the minimum annual total cost as the objective function, the mixed integer linear programming model which can optimize the equipment configuration and operation schedule is constructed.Finally, through the numerical study, the correctness and feasibility of the proposed model is verified.
Key words
zero-carbon energy system; uncertainty; LSTM quantile regression; optimal planning
随着全球化石能源的减少和环境问题的日渐突显, 世界各国推出多样化政策促进可再生能源应用。截至2020年底, 我国光伏、风电装机容量分别达到了2.5亿kW和2.8亿kW[1]。加快推进以新能源为主体的多能互补型综合能源系统成为实现碳中和、促进我国能源转型的有力措施[2]。可再生能源发电逐渐由辅助电源向主力能源转变。与传统能源系统相比, 综合能源系统中复杂设备的优化配置和合理运行调度是实现系统稳定、高效运行的核心因素。文献[3-4]以能源集线器为基本架构, 对包含风、光和天然气在内的综合能源系统设备配置进行优化。为从根本上解决化石能源引发的生态环境问题, 推动“双碳”目标实现, 有学者提出构建零碳综合能源系统。文献[5]提出并构建了一种基于风-光-沼的零碳能源电力系统, 并以系统经济性、电能质量和供电可靠性为目标对系统进行优化规划。文献[6]综合考虑偏远农村地区资源禀赋和用户负荷需求特性, 提出了以太阳能、风能和生物质能为能源输入的离网型零碳能源系统的建模与优化设计框架。作为零碳能源系统的核心要素, 风、光等可再生能源出力具有明显的间歇性、波动性, 然而既有的综合能源规划方案对此并未深究[7-8]。
关于光伏、风电的出力预测, 国内外学者已有大量研究[9-11]。近年来, 已有学者开始探讨其不确定性问题。文献[12]采用拉丁超立方抽样和K-means聚类实现了风功率典型场景获取, 有效描述了风电出力的不确定性特征。文献[13]以多场景下的期望运行成本最低为优化目标, 构建了基于多场景技术的随机优化调度模型, 但是对概率分布函数的精确度要求较高, 且需要大量的历史数据做支撑。区间数理论在处理可再生能源不确定性问题时, 建模简单且无需不确定参数的概率分布关系。文献[14]采用区间数对光伏出力及负荷的不确定性进行描述, 综合考虑多能互补和网络互联及环境效益, 建立了基于区间线性规划的区域综合能源系统日前经济优化调度模型。文献[15]建立了基于粒子群优化-区间线性规划的双层优化模型, 研究了系统内可再生能源和购能价格不确定性问题。综上所述, 针对以光伏、风电等为主体的零碳能源系统, 探讨不确定性对系统规划的影响, 目前尚未见相关报道。
本文借助区间数理论, 建立基于长短期记忆网络(Long Short-Term Memory, LSTM)分位数回归的零碳能源系统不确定性优化规划方法。首先, 构建了包含多种零碳能源技术的零碳综合能源系统物理结构, 并对系统内典型设备进行数学建模。其次, 建立光伏出力不确定性区间预测模型, 并以系统年总经济成本最小为目标函数, 构建零碳能源系统混合整数线性规划模型。最后, 通过典型算例分析, 验证所构建优化模型的可行性与有效性。
1 零碳综合能源系统
1.1 零碳能源系统物理结构
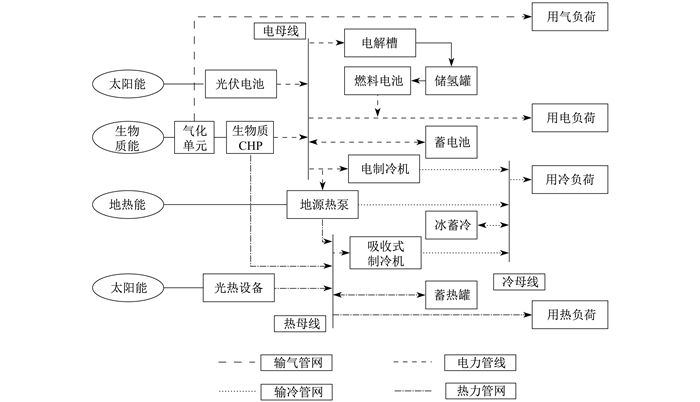
构建以零碳排放为特征的清洁能源系统, 需要依赖太阳能、风能、生物质能以及绿色氢能等零碳能源技术[16]。以满足用户冷、热、电多样化负荷需求为前提, 结合综合能源系统源网荷储一体化特征, 确定零碳能源系统物理结构如图 1所示。其中: 电负荷主要由生物质热电联产(Combined Heat and Power, CHP)机组、光伏电池、燃料电池供应; 热负荷主要由生物质CHP余热、太阳能集热器和地源热泵制热供应; 冷负荷主要由电制冷机、吸收式制冷机、地源热泵制冷供应。蓄电池、蓄热罐以及冰蓄冷设备也可满足用户负荷需求。蓄电池设备无法储存的富余电能可以通过电解槽电解水制氢储存在储氢罐中, 供后续燃料电池发电。
1.2 零碳能源系统设备模型
1.2.1 供电设备模型
生物质CHP机组采用生物质燃料热解气化再燃烧的发电方式。在任一时刻t, 生物质CHP机组终端电能输出与能量输入的关系[17]可表示为
| $ P_t^{\mathrm{BCHP}}=\frac{m_t^{\mathrm{BM}} \cdot L_{\mathrm{BM}} \cdot \eta^{\mathrm{BCHP}}}{3\;600} $ | (1) |
式中: PtBCHP——t时刻生物质CHP机组发电量;
mtBM——t时刻生物质燃料消耗量;
LBM——生物质燃料低位热值;
ηBCHP——生物质CHP机组发电效率。
光伏电池发电出力主要取决于本地太阳辐射, 其数学模型可表示为
| $ P_t^{\mathrm{PV}}= \begin{cases}\frac{N^{\mathrm{PV}} P_{\mathrm{N}} R_{\mathrm{a}\;t}^2}{R_{\mathrm{SSR}} R_{\mathrm{CR}}} & 0 \leqslant R_{\mathrm{a}\;t}<R_{\mathrm{CR}} \\ \frac{N^{\mathrm{PV}} P_{\mathrm{N}} R_{\mathrm{a}\;t}}{R_{\mathrm{SSR}}} & R_{\mathrm{CR}} \leqslant R_{\mathrm{a}\;t}<R_{\mathrm{SSR}} \\ N^{\mathrm{PV}} P_{\mathrm{N}} & R_{\mathrm{SSR}} \leqslant R_{\mathrm{a}\;t}\end{cases} $ | (2) |
式中: PtPV——t时刻光伏发电量;
NPV——光伏板数量;
PN——每个光伏板额定功率;
Ra t——t时刻本地太阳辐射强度;
RSSR——标准太阳辐射强度;
RCR——特定辐射强度。
电解槽设备可以利用富余电能电解水制氢, 而燃料电池则可利用氢能发电。其数学模型[18]分别表示为
| $ m_{t, \mathrm{H}_2}^{\mathrm{ELZ}}=\frac{P_t^{\mathrm{ELZ}} \cdot \eta^{\mathrm{ELZ}}}{L_{\mathrm{H}_2}} $ | (3) |
| $ P_t^{\mathrm{FC}}=\eta^{\mathrm{FC}} \cdot m_{t, \mathrm{H}_2}^{\mathrm{FC}} \cdot L_{\mathrm{H}_2} $ | (4) |
式中: mt, H2ELZ——t时刻电解槽电解水产生氢气质量;
PtELZ——t时刻电解槽消耗电能;
ηELZ——电解槽制氢效率;
LH2——氢的低位热值;
PtFC——t时刻燃料电池发电量;
ηFC——燃料电池发电效率;
mt, H2FC——t时刻燃料电池发电消耗氢气量。
1.2.2 供热设备模型
地源热泵的数学模型可表示为
| $ H_t^{\mathrm{GSHP}}=\left(1-f^{\mathrm{GSHP}}\right) \cdot P_t^{\mathrm{GSHP}} \cdot I_{\mathrm{H}}^{\mathrm{GSHP}} $ | (5) |
| $ C_t^{\mathrm{GSHP}}=f^{\mathrm{GSHP}} \cdot P_t^{\mathrm{GSHP}} \cdot I_{\mathrm{C}}^{\mathrm{GSHP}} $ | (6) |
式中: HtGSHP、CtGSHP——t时刻地源热泵的热出力和冷出力;
fGSHP——取0或1, 表示地源热泵设备不能同时制热和制冷;
PtGSHP——t时刻地源热泵输入的电功率;
IHGSHP、ICGSHP——地源热泵的制热、制冷能效系数。
太阳能集热器可以把太阳辐射能转换为热能, 其数学模型可表示为
| $ H_t^{\mathrm{PT}}=A^{\mathrm{PT}} \cdot R_{\mathrm{a}\;t} \cdot \eta^{\mathrm{PT}} $ | (7) |
式中: HtPT——t时刻太阳能集热器的热出力;
APT——集热板面积;
ηPT——太阳能集热器效率。
1.2.3 供冷设备模型
电制冷机的数学模型可表示为
| $ C_t^{\mathrm{ER}}=P_t^{\mathrm{ER}} \cdot I_{\mathrm{c}}^{\mathrm{ER}} $ | (8) |
式中: CtER——t时刻电制冷机冷出力;
PtER——t时刻电制冷机消耗电能;
IcER——电制冷机制冷性能系数。
吸收式制冷机是依靠吸收器-发生器将热能转化为冷负荷的设备, 可表示为
| $ C_t^{\mathrm{AC}}=H_t^{\mathrm{AC}} \cdot I_{\mathrm{c}}^{\mathrm{AC}} $ | (9) |
式中: CtAC——t时刻吸收式制冷机冷出力;
HtAC——t时刻吸收式制冷机输入热量;
IcAC——吸收式制冷机性能系数。
1.2.4 储能设备模型
蓄电、蓄冷/热、储氢设备数学模型类似, 在储存过程中会有部分损耗。以储氢设备为例, 任意时刻, 储氢设备状态均等同于前一时刻储氢罐状态值与当前时间段内储氢罐储放氢净值之和, 其数学模型可表示为
| $ G_{t+{\mathit{\Delta}} t}^{\mathrm{HST}}=\left(1-\lambda^{\mathrm{HST}}\right) G_t^{\mathrm{HST}}+\eta_{\mathrm{in}}^{\mathrm{HST}} G_{t, \text { in }}^{\mathrm{HST}} {\mathit{\Delta}} t-\frac{G_{t, \text { out }}^{\mathrm{HST}}}{\eta_{\text {out }}^{\mathrm{HST}}} {\mathit{\Delta}} t $ | (10) |
式中: Gt+ΔtHST、GtHST——(t+Δt), t时刻储氢罐的储氢量;
λHST——储氢罐的自放能率;
ηinHST、ηoutHST——储氢罐储、放氢效率;
Gt, inHST、Gt, outHST——t时刻储、放氢量。
2 可再生能源发电区间预测模型
2.1 区间线性规划
区间线性规划是将区间数理论应用于线性规划中, 并且在目标函数或约束条件中含有区间数的一类线性规划。采用区间数描述光伏出力的不确定性, 其公式为
| $ P_t^{\mathrm{PV}}=P_{t, \mathrm{y}}^{\mathrm{PV}}+{\mathit{\Delta}} P_t^{\mathrm{PV}} $ | (11) |
式中: PtPV——t时刻光伏实际出力;
Pt, yPV——光伏出力预测值;
ΔPtPV——光伏出力预测误差值。
2.2 LSTM分位数回归模型
2.2.1 分位数回归
回归分析是一种预测性建模技术。传统回归分析可反映自变量与因变量的条件期望间关系, 但难以清晰反映变量数据分布较分散或非对称分布情形, 而光伏发电功率的序列往往呈现非对称分布, 采用传统回归分析无法精准分析因变量的影响因素。分位数回归在传统回归分析得到因变量中央趋势的基础上, 能够进一步推论因变量的条件概率分布, 从而有效反映解释变量在不同分位点下对被解释变量的影响, 即分位数回归能细致地反映输入信息在不同范围内对响应变量的映射信息。其公式为
| $ \begin{aligned} Q_Y(\tau \mid \boldsymbol{X})= & \beta_0(\tau)+\beta_1(\tau) x_1+\beta_2(\tau) x_2+ \\ & \cdots+\beta_s(\tau) x_s+\varepsilon(\tau) \end{aligned} $ | (12) |
式中: QY——被解释变量Y在解释变量X给定下的条件分位数, 其中X=[1, x1, x2, x3, …, xs]T;
τ——分位点, τ∈(0, 1);
β0、β1、β2、…、βs——回归系数向量β(τ)的分量, β(τ)=[β0, β1, β2, …, βs]T, 其值随分位点τ的变化而变化;
ε(τ)——不同分位点τ的误差项。
2.2.2 LSTM人工神经网络
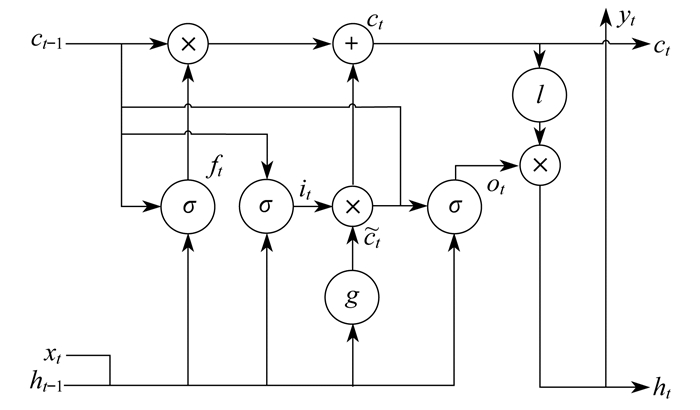
循环神经网络(Recurrent Neural Network, RNN)能够实现对序列数据的有效处理, 但当RNN对长序列进行学习时, 会出现梯度爆炸和梯度消失现象, 容易导致RNN无法掌握长时间跨度的非线性关系。为了解决RNN的长期依赖问题, LSTM理念被提出。其主要单元结构如图 2所示。图 2这样一个矩形框被称作LSTM的一个元胞, 由输入门it、输出门ot、遗忘门ft、隐藏状态ht、存储单元ct、激活函数σ等组成。LSTM神经网络在时刻t的输入数据为xt, 输出值为ht, 记忆状态为ct,
由图 2可以看出, 上一时刻隐含层传入的值ht-1和当前时刻输入值xt在遗忘门中通过计算丢弃无效的信息, 即
| $ f_t=\sigma\left(\boldsymbol{w}_{\mathrm{f}} \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_{\mathrm{f}}\right) $ | (13) |
计算得到的新信息再经过一个Sigmoid函数决定要更新哪些信息, 求取需要输入到记忆单元中的数据。tanh层创造了一个新的候选值
| $ i_t=\sigma\left(\boldsymbol{w}_{\mathrm{i}} \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_{\mathrm{i}}\right) $ | (14) |
| $ \tilde{c}_t=\tanh \left(\boldsymbol{w}_{\mathrm{c}} \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_{\mathrm{c}}\right) $ | (15) |
再将元胞的旧状态
| $ c_t=f_t c_{t-1}+i_t \widetilde{c}_t $ | (16) |
最后, 利用经过tanh层处理的新单元状态值
| $ o_t=\sigma\left(\boldsymbol{w}_{\mathrm{o}} \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_{\mathrm{o}}\right) $ | (17) |
| $ h_t=o_t \tanh \left(c_t\right) $ | (18) |
式中: w——权重矩阵;
b——偏置向量;
下标f、i、c、o——遗忘门、输入门、存储单元和输出门的对应项;
σ(·)——Sigmoid激活函数;
tanh(·)——双曲正切激活函数。
2.2.3 基于LSTM的分位数回归模型
为得到更加准确、范围更小的光伏出力预测区间, 基于神经网络分位数回归模型的特点[20], 结合LSTM回归模型, 构建LSTM分位数回归模型。该模型最终可将参数估计看作是优化问题, 利用Adam随机梯度下降法求解该优化问题[21]。具体模型如下
| $ \min \left[f_{\cos t}+\frac{\lambda}{2}|(\tilde{\boldsymbol{w}}(t), \tilde{\boldsymbol{b}}(t))|^2\right] $ | (19) |
式中: fcost——分位数回归的目标函数;
设LSTM网络中隐含层神经元为K个, 则t时刻隐含层输出的向量为Ht1, Ht2, …, Htk。将隐含层输出向量作为全连接层输入即可得到LSTM网络在分位点下的输出值为
| $ Q_Y(\tau \mid \boldsymbol{X})=g\left(\sum\limits_{k=1}^K \boldsymbol{w}_k(\tau) H_t^k+\boldsymbol{b}(\tau)\right) $ | (20) |
式中: g(·)——线性激活函数;
wk(τ)、b(τ)——LSTM隐含层输出与全连接层输入之间的权重矩阵和偏置向量。
2.3 极限场景法
3 零碳能源系统不确定性优化规划模型
3.1 目标函数
系统年总经济成本Wtotal包括设备年均总投资成本Ztotal, 设备年总维护费用Mtotal, 系统年运行费用Utotal。零碳能源系统的优化规划目标是系统年总经济成本Wtotal最小, 其公式为
| $ \min W_{\text {total }}=Z_{\text {total }}+M_{\text {total }}+U_{\text {total }} $ | (21) |
3.2 约束条件
3.2.1 能量平衡约束
根据系统供能设备出力和用户负荷形式差异, 能量平衡体现在电、热、冷3个方面, 公式为
| $ \begin{array}{l} P_t^{\mathrm{BCHP}}+\left(P_{t, \mathrm{y}}^{\mathrm{PV}}+{\mathit{\Delta}} P_t^{\mathrm{PV}}\right)+P_t^{\mathrm{FC}}+P_{t, \mathrm{out}}^{\mathrm{SBT}}=P_{t, 1}^{\mathrm{U}}+ \\ \;\;\;\;\;\;P_t^{\mathrm{ELZ}}+P_t^{\mathrm{GSHP}}+P_t^{\mathrm{ER}}+P_t^{\mathrm{IM}}+P_t^{\mathrm{MI}}+P_{t, \mathrm{in}}^{\mathrm{SBT}} \end{array} $ | (22) |
| $ \begin{aligned} & H_t^{\mathrm{BCHP}}+H_t^{\mathrm{GSHP}}+H_t^{\mathrm{PT}}+H_{t, \text { out }}^{\mathrm{HSD}}= \\ & H_{t, 1}^{\mathrm{U}}+H_t^{\mathrm{AC}}+H_{t, \text { in }}^{\mathrm{HSD}} \end{aligned} $ | (23) |
| $ C_t^{\mathrm{GSHP}}+C_t^{\mathrm{ER}}+C_t^{\mathrm{AC}}+C_{t, \text { out }}^{\mathrm{ISD}}=C_{t, 1}^{\mathrm{U}}+C_{t, \mathrm{in}}^{\mathrm{ISD}} $ | (24) |
式中: Pt, lU、Ht, lU、Ct, lU——用户电、热、冷负荷需求;
PtIM+PtMI——冰蓄冷空调制冰和融冰消耗电功率;
Pt, inSBT、Pt, outSBT——t时刻蓄电池的充、放电功率;
HtBCHP——生物质CHP机组余热;
Ht, inHSD、Ht, outHSD——t时刻蓄热罐的储、放热量。
3.2.2 供能设备运行约束
供能系统中发电设备、供热设备、供冷设备出力需满足其正常工作范围的上下限, 即
| $ E_{\min }^k \leqslant E_t^k \leqslant E_{\max }^k $ | (25) |
式中: Emink、Emaxk——第k个设备正常运行所允许的最小、最大出力值;
Etk——第k个供能设备t时刻输出能量。
光伏板面积受到场地实际情况的制约, 应满足以下约束
| $ 0 \leqslant A^{\mathrm{PV}}+A^{\mathrm{PT}} \leqslant S $ | (26) |
式中: APV——光伏板占地面积;
S——实际情况所允许光伏板和光热设备最大占地面积。
电解槽运行约束为
| $ P_{\min }^{\mathrm{ELZ}} \leqslant P_t^{\mathrm{ELZ}} \leqslant P_{\max }^{\mathrm{ELZ}} $ | (27) |
式中: PminELZ、PmaxELZ——电解槽空转功率和额定功率。
3.2.3 储能设备运行约束
以蓄电池为例, 定义最小能量容量来表示电池剩余能量的阈值, 并且规定蓄电池初始含电量为零, 而且蓄电池不应同时充电和放电, 其运行约束可表示为
| $ \beta \cdot P_{\max }^{\mathrm{SBT}} \leqslant P_t^{\mathrm{SBT}} \leqslant P_{\max }^{\mathrm{SBT}} $ | (28) |
| $ 0 \leqslant P_{t, \text { in }}^{\mathrm{SBT}} \leqslant P_{\text {max, in }}^{\mathrm{SBT}} $ | (29) |
| $ 0 \leqslant P_{t, \text { out }}^{\mathrm{SBT}} \leqslant \min \left(P_t^{\mathrm{SBT}}, P_{\text {max }, \text { out }}^{\mathrm{SBT}}\right) $ | (30) |
| $ P_{t, \text { out }}^{\mathrm{SBT}} \leqslant M \cdot f_{\text {out }}^{\mathrm{SBT}} $ | (31) |
| $ P_{t, \mathrm{in}}^{\mathrm{SBT}} \leqslant M \cdot f_{\mathrm{in}}^{\mathrm{SBT}} $ | (32) |
| $ f_{\text {out }}^{\mathrm{SBT}}+f_{\text {in }}^{\mathrm{SBT}} \leqslant 1 $ | (33) |
式中: β——系数, β∈(0, 1), 起到保护蓄电池的作用;
PmaxSBT——蓄电池额定容量;
Pmax, inSBT、Pmax, outSBT——蓄电池单位时间所允许的最大充、放电量;
Pt, inSBT、Pt, outSBT——t时刻蓄电池的充、放电量;
M——极大值;
finSBT、foutSBT——蓄电池充、放电的状态值, 取0或1。
因为蓄电池不能同时充放电, 所以引入极大值M对其充、放电状态进行限制。
4 算例分析
4.1 算例参数
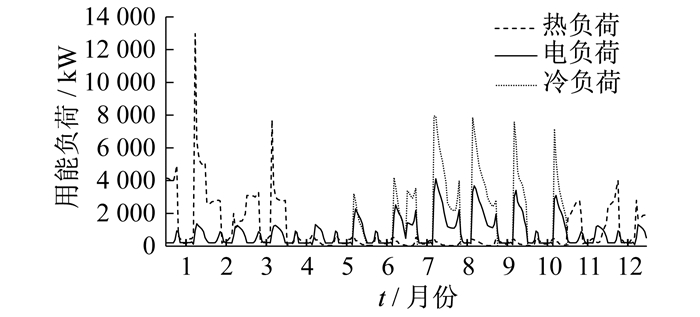
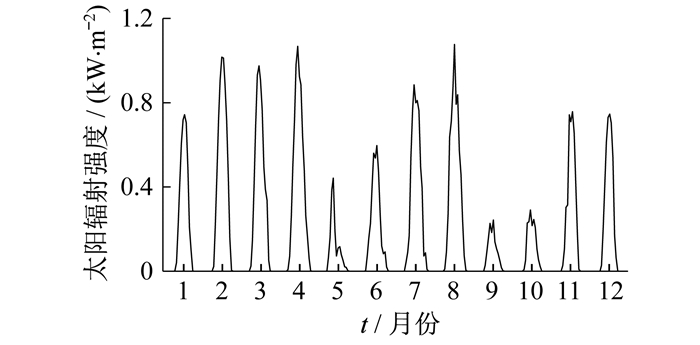
针对某典型区域, 选取每个月的15日作为典型日, 得到用户每月电、热、冷负荷需求曲线, 如图 4所示。图 5为对应的逐时太阳辐射强度。系统供、储能设备的技术和经济参数[23-24]如表 1和表 2所示。
表 1
典型设备参数
| 设备类型 | 单位容量成本/ (元·kW-1) |
单位出力维护成本/ (元·kW-1) |
效率/性能系数 | 生命周期/ a |
||
| 电 | 热 | 冷 | ||||
| 生物质CHP机组 | 10 055.00 | 0.080 0 | 0.330 0 | 0.51 | — | 20 |
| 光伏 | 7 800.00 | 0.010 0 | 0.153 8 | — | — | 20 |
| 燃料电池 | 15 000.00 | 0.200 0 | 0.380 0 | — | — | 20 |
| 光热设备 | 2 250.00 | 0.008 0 | — | 0.60 | — | 20 |
| 地源热泵 | 3 000.00 | 0.009 7 | — | 4.40 | 5.0 | 20 |
| 电制冷机 | 828.75 | 0.008 0 | — | — | 4.0 | 20 |
| 吸收式制冷机 | 1127.75 | 0.008 0 | — | — | 1.2 | 20 |
| 电解槽 | 16 170.00 | 0.014 0 | — | — | — | 20 |
表 2
储能设备参数
| 设备类型 | 单位容量成本/ (元·kWh-1) |
单位出力维护成本/ (元·kWh-1) |
储/放能效率 | 自放能率 | 生命周期/ a |
| 蓄电设备 | 1 000 | 0.001 8 | 0.95/0.95 | 0.001 | 20 |
| 蓄热设备 | 150 | 0.001 7 | 0.88/0.88 | 0.010 | 20 |
| 蓄冰槽 | 190 | 0.002 0 | 0.95/0.95 | 0.010 | 20 |
| 储氢罐 | 250 | 0.500 0 | 0.95/0.95 | 0.010 | 20 |
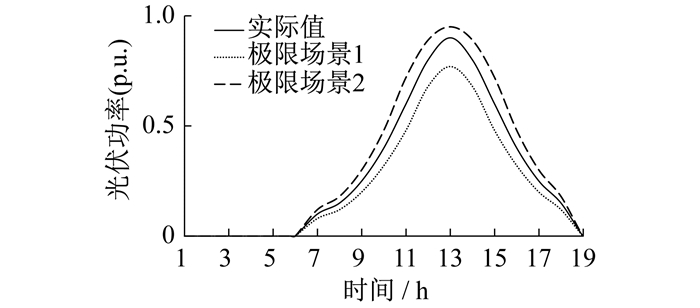
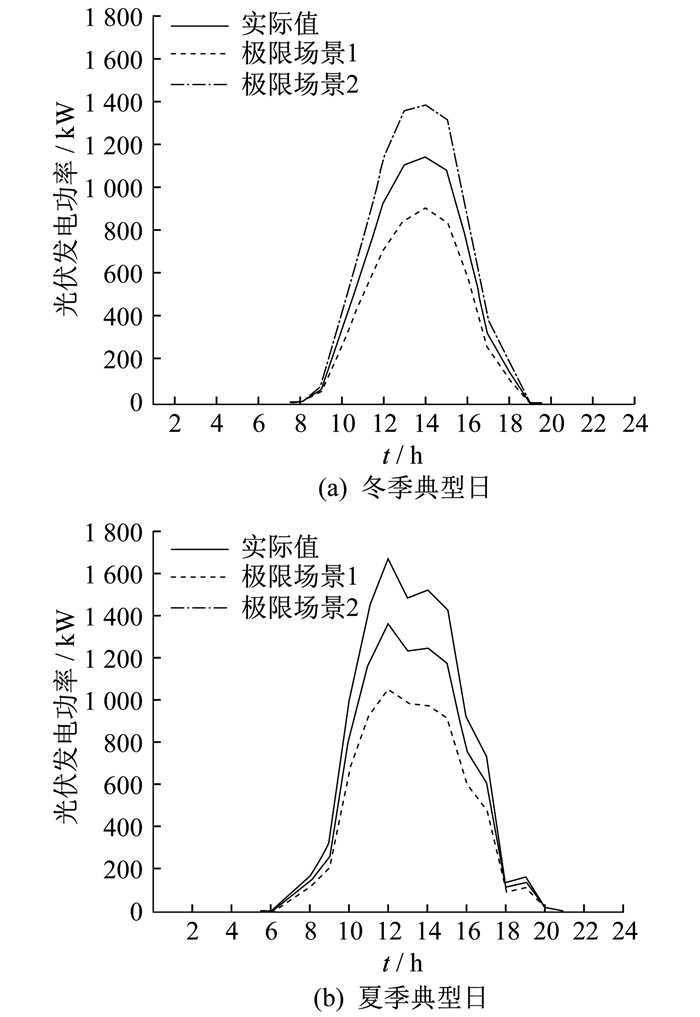
根据全年光伏逐时发电出力数据, 选取前4个月2 905个时间点的数据为训练样本, 利用LSTM分位数回归模型对典型日光伏发电功率进行区间预测。其中, 冬季和夏季典型日的光伏发电功率区间预测结果曲线如图 6所示。
4.2 优化规划结果分析
4.2.1 设备容量优化结果分析
为分析光伏出力不确定性对零碳能源系统运行的影响, 本文设定两种情景作对比, 情景1和情景2分别为不考虑和考虑光伏出力不确定性。
表 3为情景1所确定的系统最佳容量配置。对比图 1所构建的能源系统物理结构, 电制冷机和光热设备都没有选择。这主要是由于生物质CHP机组容量较大, 机组余热可推动吸收式制冷机供应全部冷负荷。用户全年热负荷需求量、需求时间固定, 生物质CHP机组和地源热泵是稳定的产热设备。同时, 由于光伏和光热设备的规划面积有一定限制, 利用太阳能发电效益远高于太阳能产热, 因此光热设备也没有选择。
表 3
情景1的零碳能源系统设备最优容量配置
| 零碳能源系统 | 设备 | 容量 |
| 供能子系统 | 生物质CHP机组 | 2 737 kW |
| 光伏电池 | 1 546 kW | |
| 燃料电池 | 236 kW | |
| 光热设备 | 0 kW | |
| 地源热泵 | 2 667 kW | |
| 电制冷机 | 0 kW | |
| 吸收式制冷机 | 4 902 kW | |
| 储能子系统 | 蓄电设备 | 4 900 kWh |
| 蓄热设备 | 6 992 kWh | |
| 蓄冷设备 | 3 451 kWh | |
| 储氢罐 | 21 m3 | |
| 其他设备 | P2G电解槽 | 442 kW |
情景2中2种极限场景下的设备配置如表 4所示。与情景1的系统容量配置相比, 由于光伏发电出力降低, 情景2的光伏容量相应减小。为进一步平衡用户电负荷需求, 生物质CHP机组容量增大, 但是燃料电池由于单位容量投资成本和出力成本都较高, 其容量没有改变。生物质CHP机组容量的增大间接导致了来自生物质余热增多, 所以系统对地源热泵的热出力依赖减小, 地源热泵容量减小, 吸收式制冷机容量增大。在极限场景1中, 储能设备的容量仅有小幅度变化, 但是在极限场景2中, 蓄电、蓄热以及蓄冷设备的容量都有不同程度增大。主要是因为光伏发电出力增加, 为提高可再生能源利用率、平抑光伏发电波动性所带来的问题, 使得蓄电池设备容量增加最多。生物质CHP机组容量相应减小, 导致可利用余热减少, 为进一步平衡系统冷热负荷需求, 地源热泵容量增大, 相应对蓄热、蓄冷设备容量配置也提出了更高要求。
表 4
情景2的零碳能源系统设备最优容量配置
| 零碳能源系统 | 设备 | 容量 | |
| 极限场景1 | 极限场景2 | ||
| 供能子系统 | 生物质CHP机组 | 2 902 kW | 2 502 kW |
| 光伏电池 | 1 282 kW | 1 901 kW | |
| 燃料电池 | 236 kW | 236 kW | |
| 光热设备 | 0 kW | 0 kW | |
| 地源热泵 | 2 453 kW | 2 848 kW | |
| 电制冷机 | 0 kW | 0 kW | |
| 吸收式制冷机 | 5 054 kW | 4 467 kW | |
| 储能子系统 | 蓄电设备 | 4 974 kWh | 7 102 kWh |
| 蓄热设备 | 6 947 kWh | 7 201 kWh | |
| 蓄冷设备 | 4 598 kWh | 4 945 kWh | |
| 储氢罐 | 28 m3 | 14 m3 | |
| 其他设备 | P2G电解槽 | 630 kW | 283 kW |
4.2.2 系统经济性分析
4.2.3 能量平衡分析
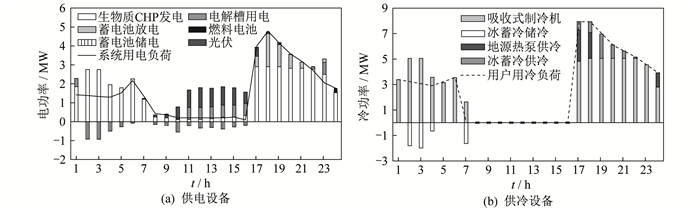
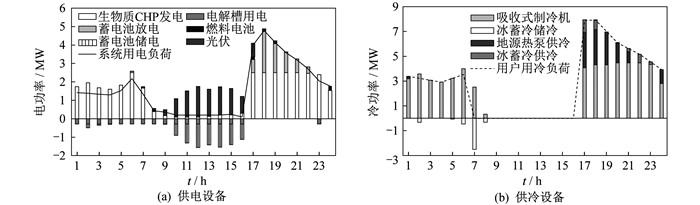
为进一步了解可再生能源不确定性对零碳能源系统运行调度的影响, 选取极限场景1和极限场景2中夏季典型日设备时序出力的运行策略进行对比分析, 结果如图 7和图 8所示。
在极限场景1中, 白天光伏发电出力在满足用户电负荷需求后, 多余电量会一部分储存在蓄电池中, 另一部分通过电解槽电解水制氢, 并存储在储氢罐中。但在极限场景2中, 白天光伏发电多余电量绝大部分都储存在蓄电池中, 这主要是因为在极限场景2中, 蓄电池设备容量大, 且直接存储在蓄电池中经济性更好。在2种场景下, 生物质CHP机组发电量均是系统主要电力来源。夜间, 光伏电池无出力, 生物质CHP机组发电量和蓄电池放电量依旧无法满足用户电负荷需求时, 系统会启动燃料电池发电。燃料电池的频繁启动会减小系统经济性, 这也解释了为何情景2的2种极限场景下系统经济成本均高于情景1。2种极限场景中, 用户冷负荷需求主要由吸收式制冷机满足, 地源热泵为供冷辅助设备, 冰蓄冷设备会在冷量较多时将多余冷量储存, 并在夜晚冷高峰时段释放。
5 结语
考虑到零碳能源系统中光伏等可再生能源的波动性和间歇性, 本文基于区间数理论, 建立了基于LSTM分位数回归的零碳能源系统不确定性优化规划模型。通过典型算例分析得到: 在当前技术经济条件下, 对于本文所探讨的小型分布式零碳能源系统, 光伏发电是必选要素, 生物质CHP发电能得益于其可控出力特性, 亦将发挥重要作用; 可再生能源出力不确定的考虑将显著影响系统配置, 实际规划过程中需要考虑最不利条件的影响; 不确定性的考虑会影响设备投资费、运行维护费等, 并最终导致系统总成本增加, 但增加比例有限。
参考文献
-
[1]孙荣富, 张涛, 和青, 等. 风电功率预测关键技术及应用综述[J]. 高电压技术, 2021, 47(4): 1129-1143.
-
[2]黎静华, 朱梦姝, 陆悦江, 等. 综合能源系统优化调度综述[J]. 电网技术, 2021, 45(6): 2256-2272.
-
[3]周钰童, 华亮亮, 黄伟, 等. 计及电热交易的区域综合能源多目标优化配置[J]. 现代电力, 2019, 36(4): 24-30.
-
[4]张子阳, 张聂鹏, 王满商, 等. 面向可再生能源高比例消纳的综合能源系统优化规划模型研究[J]. 可再生能源, 2020, 38(8): 1085-1091.
-
[5]马艺玮, 杨苹, 吴捷, 等. 孤岛型混合可再生能源发电系统的优化设计[J]. 华南理工大学学报(自然科学版), 2012, 40(11): 113-120.
-
[6]李金泽, 刘培, 李政. 偏远地区离网混合可再生能源系统建模与优化[J]. 工程热物理学报, 2021, 42(5): 1113-1118.
-
[7]开赛江, 计力, 周专, 等. 100%可再生能源综合能源系统容量优化配置[J]. 分布式能源, 2021, 6(4): 34-40.
-
[8]贾云辉, 张峰. 考虑分布式风电接入下的区域综合能源系统多元储能双层优化配置研究[J]. 可再生能源, 2019, 37(10): 1524-1532.
-
[9]姜恩宇, 季亮, 夏能弘, 等. 基于支持向量机的光伏发电功率预测[J]. 上海电力学院学报, 2015, 31(6): 511-513.
-
[10]崔承刚, 邹宇航. 基于深度学习的LSTM光伏预测[J]. 上海电力学院学报, 2019, 35(6): 544-552.
-
[11]李芬, 钱加林, 杨兴武, 等. 基于CAR模型的短期光伏发电量预测[J]. 上海电力学院学报, 2015, 31(6): 514-518.
-
[12]李美成, 梅文明, 张凌康, 等. 基于可再生能源不确定性的多能源微网调度优化模型研究[J]. 电网技术, 2019, 43(4): 1260-1270.
-
[13]吕海鹏, 希望·阿不都瓦依提, 孟令鹏. 计及源-荷预测不确定性的微电网双级随机优化调度[J]. 电力自动化设备, 2022, 42(9): 70-78.
-
[14]白牧可, 王越, 唐巍, 等. 基于区间线性规划的区域综合能源系统日前优化调度[J]. 电网技术, 2017, 41(12): 3963-3970.
-
[15]仇知, 王蓓蓓, 贲树俊, 等. 计及不确定性的区域综合能源系统双层优化配置规划模型[J]. 电力自动化设备, 2019, 39(8): 176-185.
-
[16]刘萍, 杨卫华, 张建, 等. 碳中和目标下的减排技术研究进展[J]. 现代化工, 2021, 41(6): 6-10.
-
[17]CHAUHAN A, SAINI R P. Discrete harmony search based size optimization of integrated renewable energy system for remote rural areas of Uttarakhand state in India[J]. Renewable Energy, 2016, 94: 587-604.
-
[18]刘维康, 王丹, 余晓丹, 等. 考虑电气转换储能和可再生能源集成的微能源网多目标规划[J]. 电力系统自动化, 2018, 42(16): 11-20.
-
[19]徐文秀. 基于LSTM和LDA的可再生能源领域主题分类研究[D]. 济南: 山东大学, 2020.
-
[20]TAYLOR J W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns[J]. Journal of Forecasting, 2000, 19(4): 299-311.
-
[21]黄圣权. 基于深度学习的短期电力负荷预测[D]. 广州: 广东工业大学, 2019.
-
[22]侯慧, 刘鹏, 黄亮, 等. 考虑不确定性的电-热-氢综合能源系统规划[J]. 电工技术学报, 2021, 36(增刊1): 133-144.
-
[23]周灿煌, 郑杰辉, 荆朝霞, 等. 面向园区微网的综合能源系统多目标优化设计[J]. 电网技术, 2018, 42(6): 1687-1697.
-
[24]LI J R, LIN J, ZHANG H C, et al. Optimal investment of electrolyzers and seasonal storages in hydrogen supply chains incorporated with renewable electric networks[J]. IEEE Transactions on Sustainable Energy, 2019, 11(3): 1773-1784.