|
|
|
发布时间: 2023-04-28 |
其他研究 |
|
|
|
收稿日期: 2022-09-10
基金项目: 国家自然科学基金(61905139)
中图法分类号: P747
文献标识码: A
文章编号: 2096-8299(2023)02-0189-06
|
摘要
提出一种基于混合粒子群算法和细菌觅食算法的温度控制器,重点研究了菌群优化粒子群(BFO-PSO)算法的性能,包括突变、交叉、步长变化、趋化步骤和细菌的生命周期等。利用MATLAB仿真平台将其与传统比例积分微分算法(PID)及粒子群算法(PSO)进行控制效果对比,发现该方法效率高。与传统PID和PSO调节的PID相比,细菌觅食优化算法的智能PID在系统响应速度和系统稳定性能上都有很大的提高。
关键词
低温多效蒸馏海水淡化法; 温度控制; BFO-PSO算法
Abstract
A temperature controller based on hybrid particle swarm optimization (PSO) and bacterial foraging algorithm is proposed.The performance of PSO is studied, including mutation, crossover, step size change, chemotactic step and bacterial life cycle.The MATLAB simulation platform is used to compare the control effect with the traditional PID controller and the particle swarm optimization (PSO), and it is found that the method has higher efficiency.Compared with traditional PID and PSO, the intelligent PID of bacteria foraging optimization algorithm has a great improvement in the system response speed and system stability performance.
Key words
low temperature pleiotropic seawater desalination; temperature control; BFO-PSO algorithm
由于人口、工业化和现代化的迅速增长, 水资源短缺问题突显。海水淡化是解决全球饮用水日益增长需求的重要手段。海水淡化中容易出现设备结垢腐蚀情况。研究发现, 低温多效蒸馏(LT-MED)海水淡化法具有低温运行、耗能低、所需热源品位低等优点, 能够结合生活中的废热利用, 节约成本, 提升能量利用率[1]。相对于其他海水淡化法, LT-MED海水淡化法在我国更有优势, 因其在运行阶段考虑火力发电厂及钢厂的余热资源回收, 减少了能量浪费[2]。LT-MED海水淡化法在生产过程中对温度控制有一定的要求, 若控制不理想则会影响淡水的产量和品质, 甚至会造成管道结垢损坏设备。1效出口凝结水的温度控制尤为重要。正常运行时要求1效出口凝结水温度保持在64 ℃。如果温度过高, 海水喷淋量不足, 致使浓海水温度过高易使其中的盐分析出, 导致管道结垢最终损坏设备; 如果温度过低, 进入系统的总热量过低, 根据能量守恒, 最终的淡水产量会受到影响[3]。故控制1效出口凝结水温度极为关键。
本文针对1效出口凝结水温度惯性时滞特点, 采用菌群优化粒子群(BFO-PSO)算法进行控制。从仿真结果可以看出, BFO-PSO算法优化的控制器在快速性、稳定性和鲁棒性等方面, 都优于粒子群(Particle Swarm Optimization, PSO)算法和传统比例积分微分(Proportion Integration Differentiation, PID)控制的效果。这是因为PID控制器存在鲁棒性不强、适应性不快和协调性不好等问题。PSO法虽具有较强的全局搜索能力, 但存在局部搜索能力差以及容易陷入局部&极小解等问题。细菌觅食优化粒子群算法具有变方向搜索能力, 能够弥补PSO法的不足, 二者结合使控制效果达到最佳。
1 LT-MED海水淡化系统
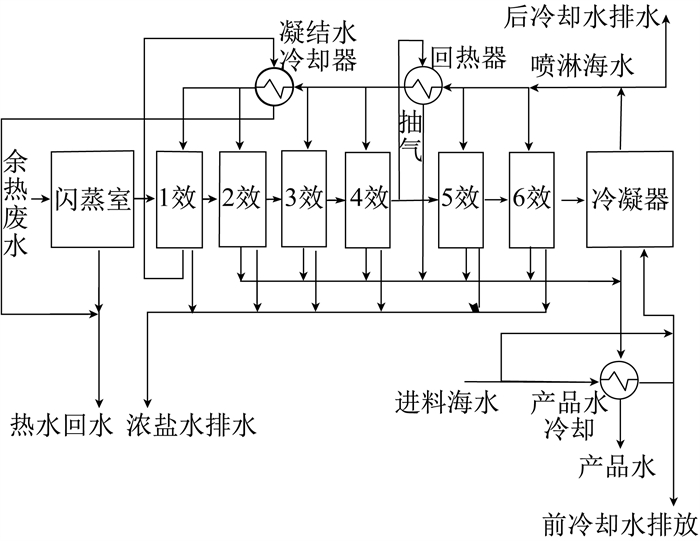
全球主流的海水淡化技术包括多级闪蒸法、低温多效蒸馏法(LT-MED)和反渗透膜法等[4]。LT-MED海水淡化法是通过真空技术降低海水沸点, 使海水的最高蒸发温度低于70 ℃。该方法能够有效减缓海水淡化过程中设备结垢和无机盐腐蚀等问题, 不仅能降低运行维护成本, 而且由于操作温度的降低, 使得设备材质要求也可以适当放宽。相对于其他海水淡化法, LT-MED海水淡化法的工艺投资和能耗较低, 这是因为只需要1效蒸发器提供一个初始热源, 其余各效均可以利用二次蒸汽的潜热进行循环蒸发。总之, LT-MED海水淡化法不仅具有结垢风险性低、动力消耗小、热效率高等特点, 而且能够高效利用生活中电厂、钢厂以及石油化工厂的废热, 提高能量的利用率。LT-MED海水淡化法总体流程如图 1所示。
LT-MED海水淡化系统包括一组各效反应室效应、冷凝器、凝结水冷却器、回热器及闪蒸罐器。热源(86 ℃的热水)从闪蒸罐被泵入1效反应室, 浓盐水通过蒸发器的冷侧。由于普遍压力较低, 给水在61.3 ℃左右沸腾, 蒸汽通过除雾器在蒸发器的热侧冷凝。在2效反应室中, 1效反应室剩余的液体与产品水从1效反应室逐级进入浓盐水闪蒸罐并在其中闪蒸以回收热量, 来自1效反应室的冷凝蒸汽(蒸发器热侧)变成纯净的蒸馏水。蒸馏物因冷凝而损失的热量在2效反应室中沸腾了更多的给水(在比1效反应室更低的压力下)。2效反应室产生的蒸汽又供给3效反应室, 依此类推, 直到最后1效反应室的蒸汽到达冷凝器, 冷凝器通常由含盐的水源冷却。每一效反应室产生的副产物卤水被收集起来, 进行下一步处理。
1.1 各效冷凝水温度特性分析
LT-MED海水淡化法中1效主要是引入物料水(海水)和热源(高炉冲渣水), 然后再分离产品水和浓盐水。热源(86 ℃的液态水)被泵入闪蒸装置, 经过闪蒸后变成蒸气泵进入1效发生器中。物料水经过凝结水冷凝器预热后进入各效蒸发器, 并等量分配到传热管的内壁, 管外为加热蒸气。1效发生器内部蒸汽与海水的能量转换总共进行了2次, 故可以将其看成二阶惯性环节。由于物料水受热蒸发出产品水后变成浓盐水的过程较短, 使得系统具有纯滞后性质。
1效产品水是由1效蒸发管内的水蒸气与管外海水进行热交换产生的。发生了一次热交换可用一阶惯性环节近似。由于温度的变化具有时滞性, 因此1效冷凝水温度系统可用传递函数来近似。
| $ G(s) = \frac{K}{{Ts + 1}}{{\rm{e}}^{ - \tau s}} $ | (1) |
式中: K——比例系数;
T——时间常数;
e-τs——延时环节。
当θ=τ/T>0.5时, 系统为大时滞系统, 参数取值为: K=6, T=7, τ=5。
1.2 产水量与1效凝结水温度关系
在输入热源量不变的情况下, 可提高总产水量与造水比。造水比公式为
| $ {P_{\rm{r}}} = \frac{{{M_{\rm{d}}}}}{{{M_{\rm{s}}}}} $ | (2) |
式中: Md——最后装置收集的淡水产品水总质量;
Ms——热源经过闪蒸装置后产生的生蒸汽流入蒸发器的质量流量。
现场研究发现, 在该系统装置不变情况下, 通过控制1效冷凝水温度可以直接影响产品水量。根据装置特性发现, 6效浓盐水温度基本稳定在45.2~45.7 ℃之间。根据能量守恒定律可知, 1效冷凝水与6效浓盐水温差越大, 则整个LT-MED海水淡化法能量利用率越高, 目标产水量也会越大。通过控制1效冷凝水温度, 可以得到满足不同工况需求的产水量。
不同工况对应1效冷凝水温度及6效浓盐水温度如表 1所示。
表 1
50 % ~100 % 工况下冷结水温度与浓盐水温度
| 工况/% | 冷结水温度/℃ | 浓盐水温度/℃ | 传热温差/K |
| 50 | 54.8 | 45.2 | 9.6 |
| 60 | 56.6 | 45.3 | 11.3 |
| 70 | 58.5 | 45.4 | 13.1 |
| 80 | 60.3 | 45.5 | 14.8 |
| 90 | 62.2 | 45.6 | 16.6 |
| 100 | 64.0 | 45.7 | 19.3 |
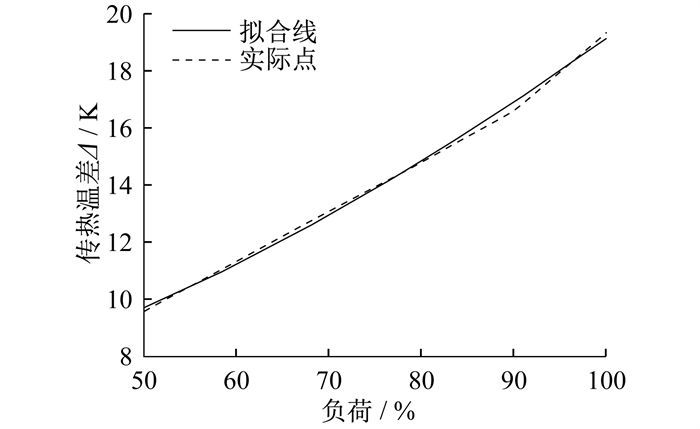
从表 1中推导出总传热温差与工况负荷的关系式为
| $ \mathit{\Delta} = 0.005015L_{\rm{r}}^{1.716} + 5.574 $ | (3) |
式中: Δ——传热温差, K;
Lr——工况负荷。
传热温差Δ与负荷拟合图如图 2所示。
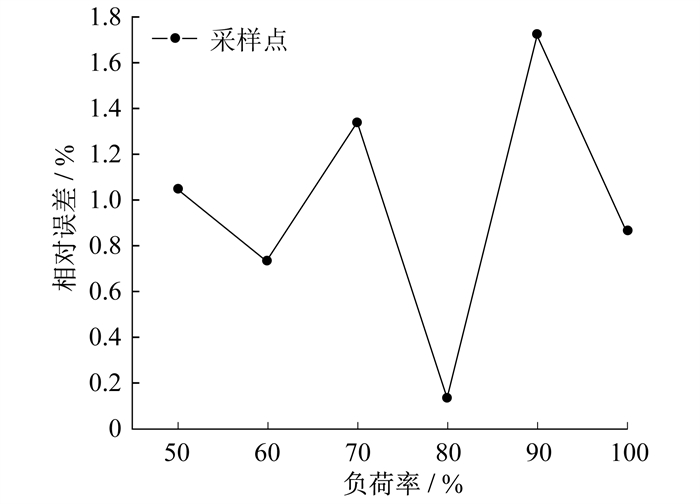
拟合后的相对误差如图 3所示。
2 PSO算法优化PID控制器
2.1 PSO算法
2.2 细菌觅食优化算法
2.2.1 细菌趋化行为
大肠杆菌是依附在动物大肠内数量最多的细菌。它的行为和运动来自一组6根刚性旋转(100~200 r/s)的鞭毛, 每根鞭毛作为一个生物马达驱动。大肠杆菌通过跑步和翻滚交替生长, 奔跑速度10~20 mm/s, 但不能直游[7]。细菌的趋化作用包括以下情形: 在中性介质中, 如果细菌交替翻滚和奔跑, 其作用类似于搜索; 如果游上一个营养梯度(或脱离有害物质), 或者细菌游得更长(爬上营养梯度或游下有害梯度), 其行为会寻求更有利的环境; 如果游过营养梯度(或有毒物质梯度), 其搜索行动就避开不利环境。因此可以推断, 细菌可以在爬上营养丘的同时, 避开有害物质。获得最佳分辨率所需要的传感器是非常敏感且具有高增益的受体蛋白[8]。也就是说, 营养物质浓度的微小变化会导致行为的显著变化。
趋化行为是细菌觅食优化算法(Bactarial Foraging Optimization, BFO)的核心, 分为翻滚行为和游动行为。在觅食过程中, 细菌沿着一定的方向寻找更好的食物。原来方向的细菌找不到更好的食物, 就进行翻转运动, 转向另一个方向[9]。在算法模拟中, 细菌的位置记录为
| $ {P_{(i, j + 1, k, 1)}} = {P_{(i, j, k, 1)}} + {C_{(i)}}{\phi _{(j)}} $ | (4) |
式中: P(i, j+1, k, 1)——趋化转向后第i个细菌的位置;
P(i, j, k, 1)——第j次趋化, 第k次繁殖, 第1次消散, 第i个细菌的位置;
C(i)——前进步长;
ϕ(j)——随机数, 表示0和1之间的翻转方向。
2.2.2 繁殖复制操作
经过趋化行为Nc次后, 细菌寻找食物能力变强, 健康度高的细菌会继续产生后代, 而健康度低和觅食能力差的细菌被淘汰。其中新生的细菌会在先前细菌的位置, 且有着等同的觅食能力。菌群经过繁殖次数Nre次后, 以细菌随机分布到新最优区域的迁移概率为Ped, 帮助算法跳出局部最优, 寻找全局最优[10]。
2.2.3 迁徙操作
迁徙操作的产生或者是细菌种群生存的当地环境逐渐发生变化部分, 或者是由于某些突然改变导致区域中的细菌迁徙到新的环境。正是通过迁移, 细菌扩散到周围环境的几乎每一个部分——从肠道到外界和地下环境。迁徙操作有可能破坏趋化过程, 但也有协助趋化的作用, 因为扩散可能会把细菌放在良好的食物来源附近。从广义上看, 种群的消除和扩散是种群长距离迁移行为的组成部分。
BFO细菌趋化和PSO粒子运动都是为了更新位置[11]。但BFO向前步长不变, 如果细菌离最优溶液有很长的距离, 则需要更多的前进; 如果过程中只是距离接近最优解, 那就可能出现错过最优解的情况。因此, 降低BFO算法的收敛速度可以通过细菌滚转的随机性以及前步的平稳性来实现。PSO算法有着较高的收敛速度, 是因为该算法可以采用局部最优值和全局最优值进行位置更新; 但该算法存在容易陷入局部最优的问题。本文结合BFO算法和PSO算法的优点, 在采用BFO算法进行趋化运动操作时进行位置更新。
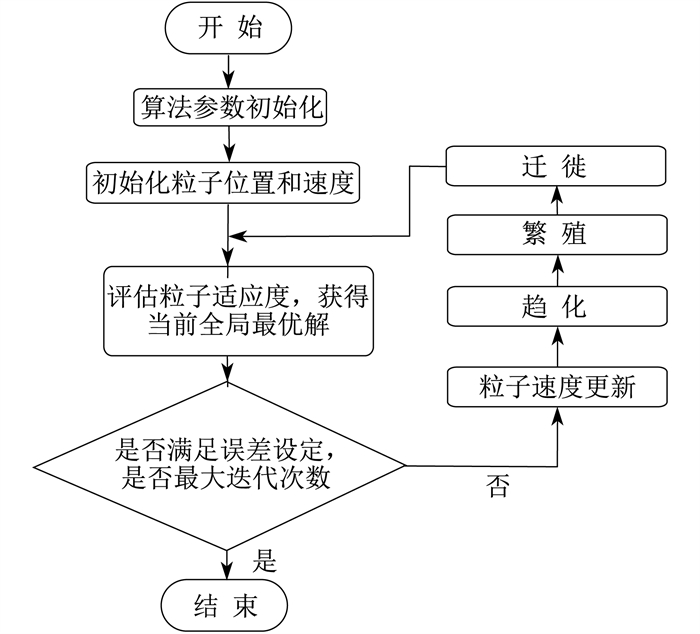
将BFO算法的趋化、繁殖、迁徙引入PSO算法, 形成BFO-PSO算法。算法流程如图 5所示。
BFO-PSO算法不仅利用遗传趋化操作转向的优势来确定搜索方向, 而且结合PSO算法在个体最优、群体最优时发挥对微生态群的引导作用。通过仿真表明, BFO-PSO算法收敛速度快, 不易陷入局部最优解[12]。
性能指标J是使用时间经误差积分和超调的绝对值, 为
| $ J = {\omega _1}\int_0^\infty t |e(t)|{\rm{d}}t + {\omega _2}t{\delta _0} $ | (5) |
式中: e(t)——系统误差;
ω1、ω2——权重值;
δ0——超调;
ω2tδ0——为了使系统不超调而适当增加的惩罚项。
3 仿真分析
本文的控制对象是一阶惯性时滞系统, 其传递函数为
| $ {\rm{G}}(s) = \frac{6}{{7s + 1}}{{\rm{e}}^{ - 5s}} $ | (6) |
将时滞环节1/eτs中的eτs根据泰勒级数展开为
| $ {{\rm{e}}^{\tau s}} = 1 + \tau s + \frac{{{\tau ^2}{s^2}}}{{2!}} + \frac{{{\tau ^2}{s^2}}}{{3!}} + \cdots $ | (7) |
取eτs=1+τs, 那么时滞环节的传递函数为1/(τs+1)。系统能够等效成二阶惯性系统。其传递函数为
| $ G(s) = \frac{6}{{(7s + 1)(5s + 1)}} $ | (8) |
BFO算法参数设置为: 细菌数量S=15, 趋化行为次数Nc=4, 繁殖行为次数Nre=4, 种群迁徙消散次数Ned=2, 前移最大长度Ns=15, 趋化步长C=0.5, 需要满足的迁徙概率Ped=0.25。PSO算法参数: c1=1.2, c2=0.5。
利用SIMULINK仿真平台对控制对象进行PID调节、PSO优化和BFO-PSO优化仿真实验。系统仿真参数如表 2所示。
表 2
系统仿真参数
| 控制方式 | 比例系数 | 积分系数 | 微分系数 |
| PID | 0.37 | 0.19 | 3.04 |
| PSO | 0.36 | 0.35 | 13.48 |
| BFO-PSO | 0.30 | 0.03 | 0.40 |
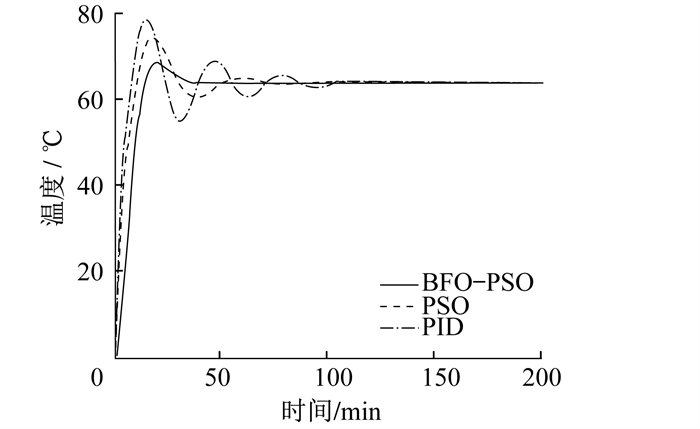
仿真效果如图 6所示。
由图 6可知, BFO-PSO算法控制的系统调节时间约为40 min, 具有较小的超调, 能以较快的速度稳定下来; PSO算法控制的系统调节时间约为110 min, 具有一定的超调量; PID算法控制的系统调节时间约为180 min, 具有较大的超调和震荡。此外, 在每个系统中使用时间乘绝对误差积分准则(ITAE), 其中: BFO-PSO算法控制的系统ITAE指数为46.2;PSO算法控制的系统ITAE指数为95.48;PID算法控制的系统ITAE指数为224.6。综上可以看出, BFO-PSO具有相对较好的系统稳定性以及较快的响应速度。
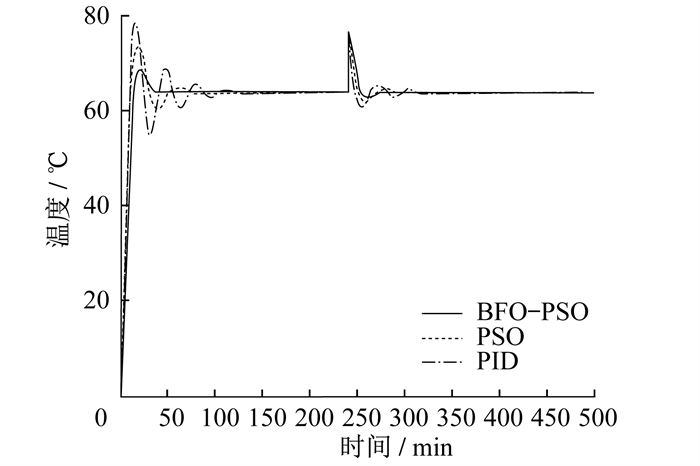
由于温度容易受到外界以及内部的干扰, 故对该系统在240 min时增加一个阶跃扰动。增加扰动后的仿真效果如图 7所示。
由图 7可以看出, 相比其他两种算法, 由BFO-PSO算法控制的系统能够在扰动后迅速恢复到给定值。这证明了BFO-PSO算法具有更强的鲁棒性。
4 结论
本文以LT-MED系统中的1效冷凝水温度系统为控制对象, 用3种控制器对系统进行仿真实验, 结论如下:
(1) 在针对温度的控制中, 引入BFO-PSO算法能够以更短的调节时间使被控系统达到稳定状态, 具有更小的超调量, 不易产生震荡。
(2) 增加扰动后, 引入BFO-PSO算法能更快回到设定值, 具有更好的鲁棒性。
参考文献
-
[1]马学虎, 兰忠, 温荣福, 等. 低温多效蒸发海水淡化系统性能的实验研究[J]. 高校化学工程学报, 2014, 28(6): 1210-1216.
-
[2]鲍克勤, 刘擘, 汤豪. 基于LADRC的低温多效蒸馏海水淡化法温度控制[J]. 昆明理工大学学报(自然科学版), 2022, 47(1): 38-45.
-
[3]解利昕, 李凭力, 王世昌. 海水淡化技术现状及各种淡化方法评述[J]. 化工进展, 2003(10): 1081-1084.
-
[4]鲍克勤, 孙蕊, 黄伟. 基于变论域模糊理论的海水淡化温控系统[J]. 计算机仿真, 2020, 37(8): 148-152.
-
[5]LIU S, WANG Z, HAN M, et al. Embodied water consumption between typical desalination projects: reverse osmosis versus low-temperature multi-effect distillation[J]. Journal of Cleaner Production, 2021, 295(6): 126340.
-
[6]EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//Mhs95 Sixth International Symposium on Micro Machine & Human Science. Nagoya, Japan: IEEE, 2002.
-
[7]闫婷. 基于混合细菌觅食和粒子群的k-means聚类算法在类风湿并发症中的研究[D]. 太原: 太原理工大学, 2016.
-
[8]张谦. 改进细菌觅食优化算法研究及应用[D]. 温州: 温州大学, 2020.
-
[9]赵平起, 何书梅, 倪天禄, 等. BFO-PSO算法下的弹性波数值模拟[J]. 地球物理学报, 2021, 64(7): 2461-2470.
-
[10]DONG H K, CHO J H. Adaptive tuning of PID controller for multivariable system using bacterial foraging based optimiza-tion[C]//Advances in Web Intelligence Third International Atlantic Web Intelligence Conference. Lodz, Poland: AWIC, 2005.
-
[11]DASGUPTA S, BISWAS A, ABRAHAM A, et al. Adaptive computational chemotaxis in bacterial foraging algorithm[C]//Complex, Intelligent and Software Intensive Systems. International Conference. Enokido, Japan: CISIS, 2008.
-
[12]LIU C, YANG C, WANG L, et al. Application and the parameter tuning of ADRC based on BFO-PSO algorithm[C]//Chinese Control & Decision Conference. Gueiyang, China: IEEE, 2013.