|
|
|
发布时间: 2023-08-28 |
新能源发电技术 |
|
|
|
收稿日期: 2023-02-20
中图法分类号: TM743
文献标识码: A
文章编号: 2096-8299(2023)04-0325-07
|
摘要
针对传统综合惯性控制在系统频率发生突变参与调频时, 调节系数适应性、灵活性较差的问题, 提出了一种基于模糊控制的双馈风电机组变系数综合惯性控制策略。首先, 分析了双馈风电机组传统综合惯性控制系数调整的必要性; 其次, 分别对虚拟惯性控制和下垂控制各自附加一个单独的模糊控制回路使调节系数随风速和频率变化量进行实时调整; 最后, 在MATLAB/Simulink中建立了三机九节点系统模型仿真, 验证了与传统固定系数综合惯性控制相比, 变系数综合惯性控制策略的适应性和灵活性更好。
关键词
风力发电; 频率调节; 综合惯性控制; 模糊控制
Abstract
Taking into account the problem of the adjustment coefficient of traditional integrated inertial control systems not being able to adapt to the changes in frequency and participation in frequency modulation when the system frequency changes, a variable coefficient integrated inertia control strategy for doubly-fed wind turbine based on fuzzy control is proposed.First, the necessity of adjusting the traditional integrated inertial control coefficient of doubly fed wind turbines is analyzed.Secondly, a separate fuzzy control loop is added to the virtual inertial control and droop control respectively to dynamically adjust the control coefficient with the wind speed and frequency variation.Finally, a three-machine nine-node system model simulation is established in Matlab/Simulink.The results show that the variable coefficient integrated inertial control strategy is more adaptive and flexible than the traditional integrated inertial control strategy.
Key words
wind power generation; frequency regulation; integrated inertial control; fuzzy control
基于“双碳”背景, 建设以新能源为主体的新型电力系统, 是推动能源向低碳转化、实现双碳目标的重大举措。随着以风电、光伏为主的新能源在新型电力系统中的占比逐年增加, 新能源机组通过逆变器、变流器等大量电力电子装置接入主网, 使电力系统整体惯量水平降低。风电本身具有强波动性和随机性, 风电功率的波动量大, 导致系统频率波动会随之变大, 系统频率稳定性受到严重威胁。
为了使电力系统稳定运行, 专家学者们对风电机组自身参与系统调频开展了大量深入研究, 并提出了多种控制策略。目前最主要的调频策略分为两类: 一类是预留有功备用参与调频的有功备用控制[1], 另一类是利用自身惯量参与系统调频的转子动能控制。有功备用控制[2]主要分为桨距角控制[3]和转子超速控制[4]。转子动能控制[5-6]主要分为虚拟惯性控制[7]、下垂控制以及两者相结合的综合惯性控制[8-10]。文献[11]研究了风电机组调频系数的约束因素, 从而确定控制系数, 但过于依赖经验。文献[12]提出了对虚拟惯性控制增加一个选择函数环节, 提高系统的等效转动惯量进而提升调频能力的优化控制方法。文献[13]提出了风-火系统模糊自适应虚拟惯量控制策略, 利用模糊控制对虚拟惯性控制系数进行控制, 但只对虚拟惯性控制进行了单独研究未考虑下垂控制。文献[14]通过在传统综合惯性控制中, 风电机组处于最大功率点跟踪(Maximum Power Point Tracking, MPPT)模式下, 附加转速优化模块改变功率-转速曲线, 使风机处于减载状态, 但经济性较差。文献[15]提出基于不同风速整定虚拟惯性控制和下垂控制的调差系数, 该策略虽根据风速变化对系数进行整定, 但所取控制系数依然为固定值。
综上, 目前针对综合惯性控制策略的研究中, 控制系数多取固定值或仅对虚拟惯性控制和下垂控制中的一个控制单独进行研究。然而控制系数取固定值时, 所选数值过小可能难以达到想要的调频效果, 所选数值过大可能超出转子可提供能量的极限导致频率二次跌落; 而仅研究虚拟惯性控制和下垂控制中的一个控制考虑不够全面。针对以上问题, 本文提出了基于模糊控制的风电机组变系数综合惯性控制策略, 对综合惯性控制中的虚拟惯性控制和下垂控制, 根据各自的取值特性分别附加一个系数, 再根据风速和频率变化量实时调整模糊控制回路, 在保证最大限度利用转子动能提供最大出力的同时, 控制系数不会超出极限值从而保证频率不会发生二次跌落。
1 综合惯性控制
1.1 传统综合惯性控制的原理
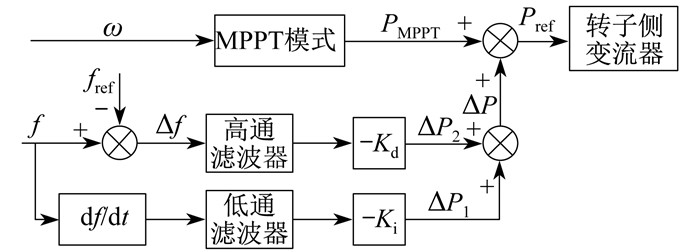
传统综合惯性控制由虚拟惯性控制和下垂控制两部分组成。传统综合惯性控制是在风电机组处于MPPT模式的基础上, 附加有功增量ΔP, ΔP由虚拟惯性控制有功增量ΔP1和下垂控制有功增量ΔP2组成。当频率发生突变时, 风机的输出参考功率Pref为
| $ P_{\mathrm{ref}}=P_{\mathrm{MPPT}}+\Delta P_1+\Delta P_2 $ | (1) |
式中: PMPPT——MPPT控制环节输出功率。
虚拟惯性控制有功增量ΔP1的公式为
| $ \Delta P_1=-K_{\mathrm{i}} \frac{\mathrm{d} f}{\mathrm{~d} t} $ | (2) |
式中: Ki——虚拟惯性控制系数;
f——频率。
下垂控制有功增量ΔP2的公式为
| $ \Delta P_2=-K_{\mathrm{d}} \Delta f $ | (3) |
式中: Kd——下垂控制系数;
Δf——频率的偏差量。
综合惯性控制示意如图 1所示, ω为风机转子转速, fref为参考频率。当系统有功功率不平衡时, 频率产生偏差, 频率变化率df/dt经过低通滤波器和虚拟惯性控制系数环节得到虚拟惯性控制有功增量ΔP1; 系统频率偏差Δf经过高通滤波器和下垂控制系数环节得到下垂控制有功增量ΔP2。有功增量与MPPT控制环节输出功率PMPPT结合得到MPPT控制环节输出功率Pref输入到转子侧变流器。
1.2 控制系数对调频能力的影响
同步机组动态响应方程为
| $ 2 H \lambda \frac{\mathrm{d} f}{\mathrm{~d} t}=P_{\mathrm{w}}+P_{\mathrm{G}}-P_{\mathrm{L}}-D \lambda \Delta f $ | (4) |
式中: H——系统惯性系数;
λ——同步机组输出有功占比;
PW——风电机组出力;
PG——同步机组出力;
PL——负荷;
D——系统下垂系数。
风机处于MPPT模式下, 附加了综合惯性控制环节后的风电机组出力PW为
| $ P_{\mathrm{W}}=P_{\mathrm{MPPT}}-K_{\mathrm{i}} \frac{\mathrm{d} f}{\mathrm{~d} t}-K_{\mathrm{d}} \Delta f $ | (5) |
将式(4)代入式(5), 得
| $ \begin{gathered} \left(2 H \lambda+K_{\mathrm{i}}\right) \frac{\mathrm{d} f}{\mathrm{~d} t}+\left(D \lambda+K_{\mathrm{d}}\right) \Delta f= \\ P_{\mathrm{MPPT}}+P_{\mathrm{G}}-P_{\mathrm{L}} \end{gathered} $ | (6) |
由式(6)可知, 系统等效惯性随着Ki的增大而增大, 系统等效阻尼随着Kd的增大而增大[16]。但是控制系数过大可能使风机过度释放动能超过动能释放极限, 导致转子转速过低而失去稳定, 从而引起频率更深程度的跌落。因此, 风电机组调频能力在很大程度上取决于Ki和Kd的取值, 对系数进行控制十分有必要。
1.3 初始风速对调频能力的影响
当风机转子初始转速为ω0时, 转子储存的动能Ek为
| $ E_{\mathrm{k}}=\frac{1}{2} J \omega_0 $ | (7) |
式中: J——转动惯量。
在风机提供有功出力阶段, 风机转子转速由ω0降低到最低转速ωmin, 双馈风机可释放的动能极限ΔEKmax为
| $ \Delta E_{\mathrm{Kmax}}=\frac{1}{2} J\left(\omega_0^2-\omega_{\min }^2\right) $ | (8) |
风机初始状态运行于MPPT模式下, 初始转速ω0为
| $ \omega_0=\frac{\lambda_{\mathrm{opt}} v_0}{r} $ | (9) |
式中: λopt——最优叶尖速比;
v0——初始风速;
r——风机叶片半径。
将式(9)代入式(8), 得
| $ \begin{aligned} \Delta E_{\mathrm{Kmax}}= & \frac{1}{2} J\left(\frac{\lambda_{\mathrm{opt}}^2 v_0^2}{r^2}-\omega_{\min }^2\right)= \\ & \frac{1}{2} \frac{J \lambda_{\mathrm{opt}}^2}{r^2} v_0^2-\frac{1}{2} J \omega_{\min }^2 \end{aligned} $ | (10) |
式(10)可进一步化简为
| $ \Delta E_{\mathrm{Kmax}}=K_1 v_0^2-K_2 $ | (11) |
| $ K_1=\frac{J \lambda_{\mathrm{opt}}^2}{2 r^2} $ | (12) |
| $ K_2=\frac{1}{2} J \omega_{\text {min }}^2 $ | (13) |
由式(11)可看出, 转子最大可释放动能和初始风速的平方近似成正比关系, 即初始风速越大, 转子释放动能极限越大, 风机有功出力极限越大, 调频极限越大。
2 变系数综合惯性控制
2.1 基于模糊控制的变系数调频策略
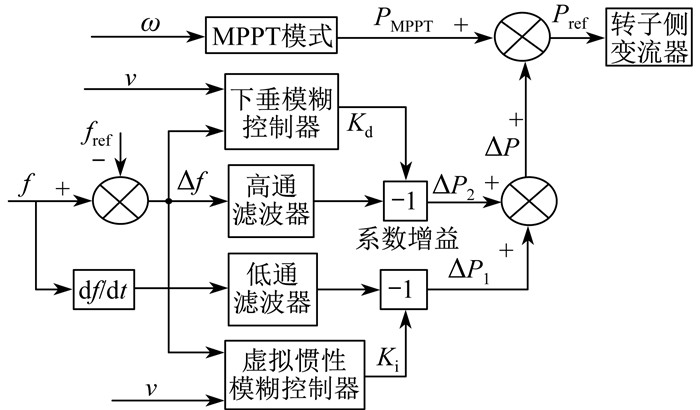
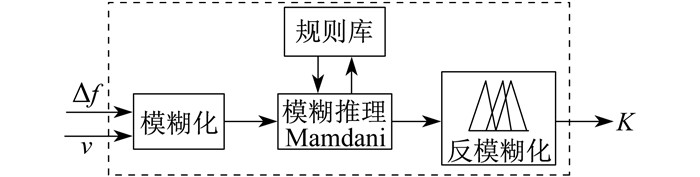
传统综合惯性控制一般选取固定的控制系数, 并未对虚拟惯性控制系数和下垂控制系数的大小进行调整。但若所选取控制系数过小, 风机将不能提供足够的有功出力, 无法达到想要的调频效果; 若所选控制系数过大, 可能造成风机失稳甚至系统频率二次跌落[17]。已有文献大多针对频率变化量、转子转速或风速来调整综合惯性控制中的一个控制系数, 较少同时考虑风速和频率变化对综合惯性控制的整体影响。本文所设计的模糊控制器的输入为风速v和频率变化量Δf, 以虚拟惯性控制系数Ki、下垂控制系数Kd分别作为两个控制器的输出设计模糊控制器, 使风机的调频能力跟随风速及频率变化动态调整。变系数综合惯性控制示意如图 2所示, 模糊控制器结构如图 3所示。
图 2中, 当系统频率产生偏差时, 风速v和频率偏差量Δf通过虚拟惯性模糊控制器输出实时虚拟惯性控制系数的值, 频率变化率df/dt经过低通滤波器与实时虚拟惯性控制系数结合通过系数增益环节得到虚拟惯性控制有功增量ΔP1; 风速v和频率偏差量Δf通过下垂模糊控制器输出实时下垂控制系数的值, 系统频率偏差Δf经过高通滤波器和实时下垂控制系数结合通过系数增益环节得到下垂控制有功增量ΔP2。有功增量与MPPT控制环节输出功率PMPPT结合得到输出参考功率Pref输入到转子侧变流器。
图 3中, 将频率偏差Δf和风速v的数字量信号转化为模糊量, 将模糊量作为模糊规则的输入, 经过模糊规则库得到输出量,然后将输出量通过反模糊转换为精确量即控制系数K。
根据系统状态和附加频率控制原理, 对模糊控制器进行设计。当Δf为正值时, 说明电力系统有功出力富余, 此时仅由传统火电机组参与调节, 风电机组不参与调频, 使系统运行更加经济。本文设计的模糊控制器仅考虑频率偏差为负值的情况。当风速较低时, 此时风机转子最大可释放动能较小, 若Δf数值较小, 控制系数取较小值, 若Δf数值较大, 控制系数可取中间值; 当风速较高时, 此时风机可提供的有功出力较大, 若Δf数值较小, 控制系数取较小值, 若Δf数值较大, 控制系数可取较高值。
2.2 虚拟惯性控制系数的动态调整
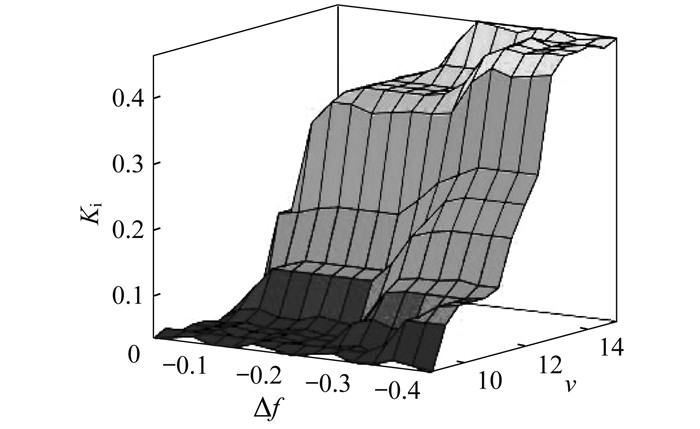
虚拟惯性模糊控制器的输入量为风速v和频率偏差量Δf, 输出量为虚拟惯性控制系数Ki。仿真所用风机的额定风速为12 m/s, 切入风速为5 m/s, 切出风速为16.2 m/s。选择15 m/s(高于额定风速低于切出风速)、9 m/s(高于切入风速低于额定风速)分别作为风速论域的上下限。风速v的基本论域为[9, 10, 11, 12, 13, 14, 15], 对应的模糊子集为{NL, NM, NS, ZO, PS, PM, PL}, 对应到语言量为负大、负中、负小、零、正小、正中、正大。频率偏差量Δf基本论域为[-0.4, -0.3, -0.2, -0.1, 0], 对应的模糊子集为{NL, NS, ZO, PS, PL}。虚拟惯性控制系数Ki的论域为[0, 0.125, 0.25, 0.375, 0.5], 对应的模糊子集为{NL, NS, ZO, PS, PL }。选择三角形作为隶属度函数, 虚拟惯性控制系数Ki模糊逻辑规则如表 1所示, 输出结果如图 4所示。
表 1
虚拟惯性控制系数Ki模糊逻辑规则
| v | Δf | ||||
| NL | NS | ZO | PS | PL | |
| NL | NL | NL | NL | NL | NL |
| NM | NS | NL | NL | NL | NL |
| NS | NS | NS | NL | NL | NL |
| ZO | ZO | ZO | NS | NS | NL |
| PS | PL | PS | PS | ZO | NL |
| PM | PL | PL | PS | PS | NL |
| PL | PL | PL | PL | PS | NL |
2.3 下垂控制系数的动态调整
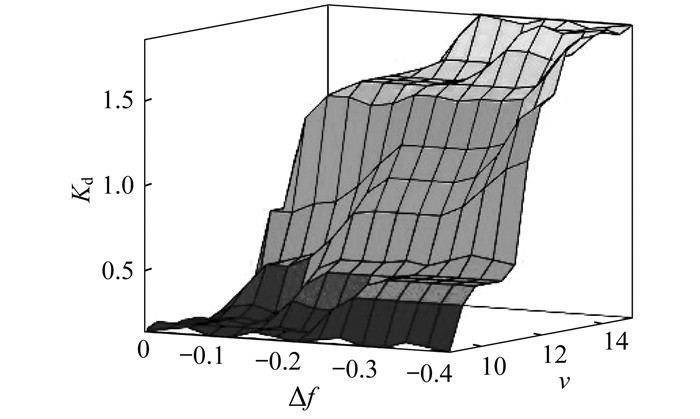
下垂模糊控制器的输入量为风速v和频率偏差量Δf, 输出量为下垂控制系数Kd。风速v的基本论域为[9, 10, 11, 12, 13, 14, 15], 对应的模糊子集为{NL, NM, NS, ZO, PS, PM, PL}。频率偏差量Δf基本论域为[-0.4, -0.3, -0.2, -0.1, 0], 对应的模糊子集为{NL, NS, ZO, PS, PL}。下垂控制系数Kd的论域为[0, 0.5, 1, 1.5, 2], 对应的模糊子集为{NL, NS, ZO, PS, PL}。下垂控制系数Kd模糊逻辑规则如表 2所示, 输出结果如图 5所示。
表 2
下垂控制系数Kd模糊逻辑规则
| v | Δf | ||||
| NL | NS | ZO | PS | PL | |
| NL | NL | NL | NL | NL | NL |
| NM | NS | NS | NL | NL | NL |
| NS | NS | NS | NS | NL | NL |
| ZO | PS | ZO | ZO | NS | NL |
| PS | PL | PS | PS | PS | NL |
| PM | PL | PL | PS | PS | NL |
| PL | PL | PL | PL | PS | NL |
3 算例分析
3.1 仿真系统建立
为验证本文所提风电机组参与系统调频的变系数综合惯性控制策略有效性, 基于MATLAB/Simulink平台搭建了三机九节点系统进行仿真验证, 具体如图 6所示。
系统中2台火电机组的容量均为100 MW, 风电场由35个额定容量为3.5 MW的双馈风力发电机组成, 风机的额定风速为12 m/s。恒定有功负荷分别由117 MW、35 MW、95 MW、2.5 MW 4个负荷组成。在低风速和高风速两种情况下, 负荷突增之后, 仿真对比风电机组不参与调频策略(MPPT模式)、传统固定系数综合惯性控制策略(为防止系统频率二次跌落且风机可提供较大的出力, 虚拟惯量控制系数取0.4、下垂控制系数取1.5)和本文所提变系数综合惯性控制策略在各自场景下的系统频率、转子转速以及风机出力的情况。
3.2 低风速仿真分析
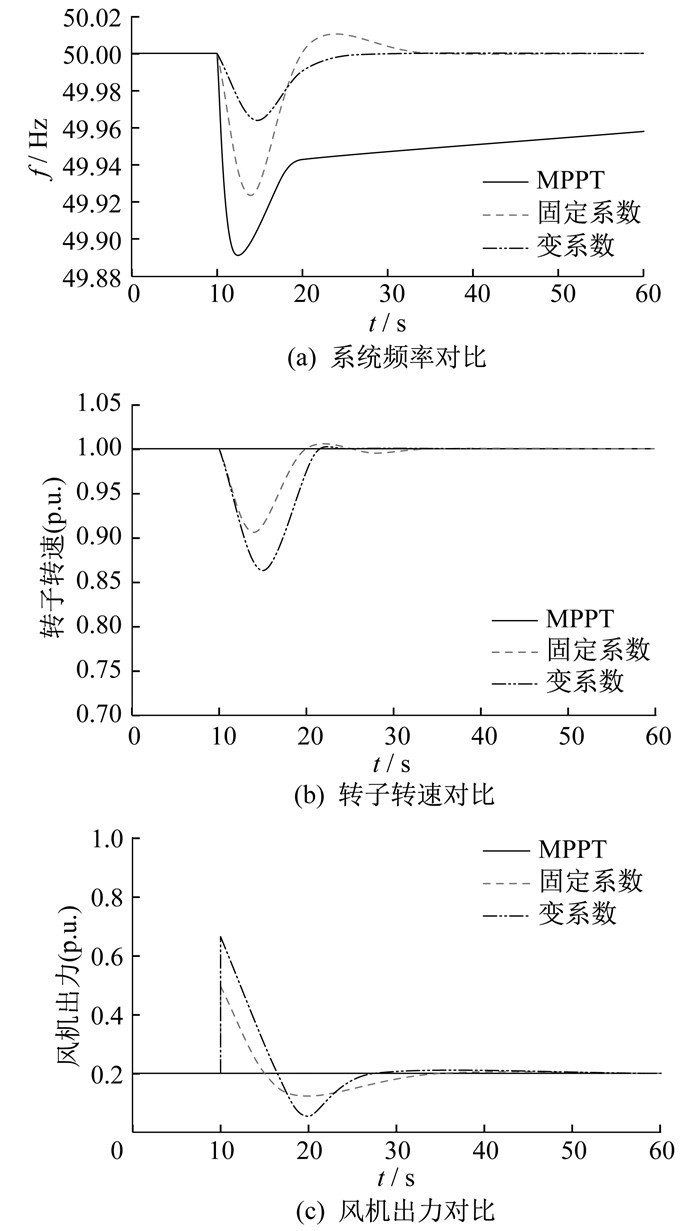
以风速论域的下限为低风速, 当风速v=9 m/s时, 在10 s时突增一个20 MW的负荷, 风电机组分别运行在MPPT模式、传统固定系数综合控制策略以及变系数综合惯性控制策略下的系统响应波形如图 7所示。
由图 7(a)可看出: 风电机组运行在MPPT模式、传统固定系数综合惯性控制策略和变系数综合惯性控制策略3种模式下, 负荷突增后的频率分别跌落至49.893 Hz、49.924 Hz、49.964 Hz; MPPT模式下系统频率跌落最大, 达到0.107 Hz; 采用传统固定系数综合惯性控制策略时频率跌落为0.076 Hz, 较MPPT模式上升了0.031 Hz, 但频率恢复期间有波动振荡、不稳定; 采用变系数综合惯性控制策略后频率跌落仅为0.036 Hz, 较传统固定系数综合惯性控制策略提升了0.040 Hz, 调频效果更好且后续频率恢复过程比较平稳没有振荡。
由图 7(b)可看出: 风机转子在MPPT模式下不会对系统频率变化做出反应, 转子转速保持在1.00 p.u.; 采用传统固定系数综合惯性控制策略时, 风机转子转速下降至0.906 p.u., 但恢复过程缓慢且伴随着振荡; 采用变系数综合惯性控制策略后, 转子转速下降至0.863 p.u., 可提供更多出力, 恢复较快且平稳。
由图 7(c)可看出: 风机在MPPT模式下有功出力无变化, 维持在0.200 p.u.; 采用传统固定系数综合惯性控制策略时, 风机出力为0.495 p.u.。采用变系数综合惯性控制策略后, 风机出力可达到0.663 p.u., 比传统固定系数综合惯性控制策略出力多0.168 p.u.且后续恢复较快。
3.3 高风速仿真分析
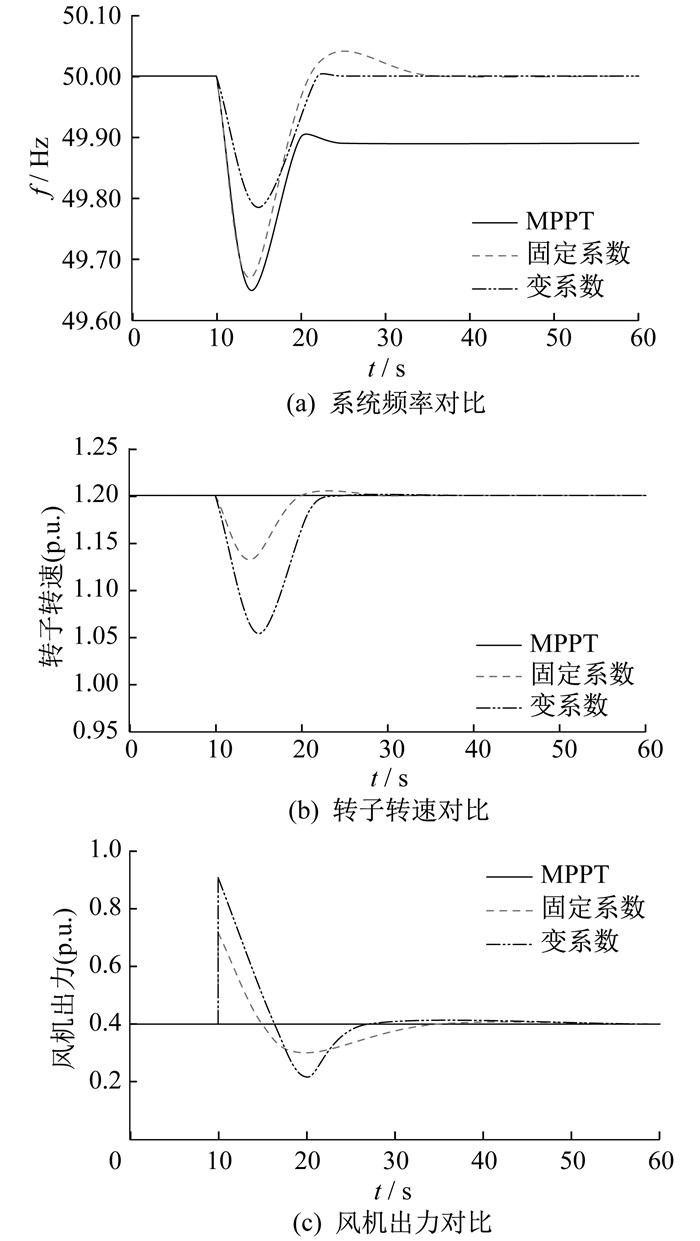
以风速论域的上限为高风速, 当风速v=15 m/s时, 在10 s时突增一个45 MW的负荷, 风电机组分别运行在MPPT模式、传统固定系数综合惯性控制策略以及变系数综合惯性控制策略下的系统仿真响应波形如图 8所示。
由图 8(a)可知: 风电机组运行在MPPT模式下系统频率跌落最大至49.657 Hz, 频率稳定性最差; 采用传统固定系数综合惯性控制策略的频率跌落较MPPT模式微提升, 至49.672 Hz, 后续频率恢复阶段波动较大; 采用变系数综合惯性控制策略后频率最大跌落明显提升, 至49.785 Hz, 相较前两种模式, 频率最大跌落深度分别提升38.57%、34.85%, 且频率恢复平稳。
由图 8(b)可知: MPPT模式下风机转子转速无变化; 传统固定系数综合惯性控制策略下转子可提供动能有限, 转子转速仅下降至1.132 p.u.; 而变系数综合惯性控制策略在调频过程中系数可调整至较大值, 使转子提供更多动能, 转子转速可降至1.054 p.u., 同时系数也不会超出极限值造成频率二次跌落。
由图 8(c)可知: 风机出力情况与低风速时特性基本一致, MPPT模式下风机出力不变, 变系数综合惯性控制策略较传统固定系数综合惯性控制策略出力多0.084 p.u., 响应速度更快, 后续恢复更快且平稳。
4 结语
本文针对风电机组参与调频问题, 提出了一种控制系数跟随风速和频率变化量动态调整的综合惯性控制策略。通过仿真结果可以看出变系数综合惯性控制策略相较于传统固定系数综合惯性控制策略的调频效果更好, 可使频率最大跌落值更小, 跌落更慢, 且频率恢复更平稳, 转速恢复更快, 系统更稳定, 即可为系统提供最大出力的同时保证系统频率的稳定性; 并且在不同的风速、频率变化量等场景下, 根据实时情况改变调整系数, 可使调频能力达到最优状态且较为经济。
本文所提变系数综合惯性控制策略属于转子动能控制。由于风机转子转速变化范围有限, 转子动能控制所能提供的动能也有限, 因此可以进一步考虑将转子动能控制和有功备用控制相结合, 根据各自的特性制定控制策略, 提高调频能力的同时兼具经济性。
参考文献
-
[1]蔡文亮, 赵正晖, 汪洋, 等.面向新型能源结构的系统调频技术回顾与展望[J/OL].电测与仪表: 1-12[2023-02-18].http://kns.cnki.net/kcms/detail/23.1202.TH.20221103.1140.006.html.
-
[2]ABOUZEID S I, GUO Y, ZHANG H C, et al. Improvements in primary frequency regulation of the grid-connected variable speed wind turbine[J]. IET Renewable Power Generation, 2019, 13(3): 491-499. DOI:10.1049/iet-rpg.2018.5187
-
[3]张三洪, 党杰, 戴剑丰, 等. 考虑最优转速与桨距角控制的风电场限功率优化控制策略[J]. 电网技术, 2021, 45(5): 1844-1851.
-
[4]蔡国伟, 钟超, 吴刚, 等. 考虑风电机组超速减载与惯量控制的电力系统机组组合策略[J]. 电力系统自动化, 2021, 45(16): 134-142.
-
[5]CHENG Y, AZIZIPANAH-ABARGHOOEE R, AZIZI S, et al. Smart frequency control in low inertia energy systems based on frequency response techniques: a review[J]. Applied Energy, 2020, 279: 115798. DOI:10.1016/j.apenergy.2020.115798
-
[6]YOO J I, KANG Y C, YANG D, et al. Power smoothing of a variable-speed wind turbine generator based on a two-valued control gain[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2765-2774. DOI:10.1109/TSTE.2020.2975061
-
[7]曹新慧, 刘昱良, 苗世洪, 等. 考虑参数自适应的直流微电网DC/DC变换器虚拟惯性控制策略研究[J]. 高电压技术, 2020, 46(4): 1281-1290.
-
[8]毛颖群, 张建平, 程浩忠, 等. 考虑频率安全约束及风电综合惯性控制的电力系统机组组合[J]. 电力系统保护与控制, 2022, 50(11): 61-70.
-
[9]吴启帆, 宋新立, 张静冉, 等. 电池储能参与电网一次调频的自适应综合控制策略研究[J]. 电网技术, 2020, 44(10): 3829-3836.
-
[10]赵熙临, 曹娅. 采用模糊规则的风机超速区变参数综合惯性控制方法[J]. 华侨大学学报(自然科学版), 2021, 42(2): 238-244.
-
[11]乔颖, 郭晓茜, 鲁宗相, 等. 考虑系统频率二次跌落的风电机组辅助调频参数确定方法[J]. 电网技术, 2020, 44(3): 807-815.
-
[12]李少林, 王伟胜, 张兴, 等. 风力发电对系统频率影响及虚拟惯量综合控制[J]. 电力系统自动化, 2019, 43(15): 64-70.
-
[13]柯贤波, 张文朝, 李朋旺, 等. 高风电渗透率系统的模糊自适应虚拟惯量控制[J]. 电网技术, 2020, 44(6): 2127-2136.
-
[14]徐鹏超, 李琰, 田新首, 等. 附加转速优化虚拟惯性控制的双馈风机一次调频研究[J]. 科学技术与工程, 2020, 20(23): 9400-9407.
-
[15]李颖颖, 王德林, 范林源, 等. 双馈风电机组限功率运行下频率稳定的变系数控制策略[J]. 电网技术, 2019, 43(8): 2910-2917.
-
[16]袁佳豪, 王维庆, 王海云, 等. 双馈风电机组变系数综合惯性策略优化控制[J]. 现代电子技术, 2022, 45(21): 97-102.
-
[17]柯贤波, 王青, 张钢, 等. 适应双馈风机的改进频率主动控制策略[J]. 电力系统及其自动化学报, 2022, 34(12): 100-105.