|
|
|
发布时间: 2023-08-28 |
新能源发电技术 |
|
|
|
收稿日期: 2023-04-04
中图法分类号: TM743
文献标识码: A
文章编号: 2096-8299(2023)04-0317-08
|
摘要
由于光伏逆变器与有源滤波器具有相同的拓扑结构, 因此将光伏逆变器与有源滤波器相结合有利于提高光伏并网效率。准比例谐振(PR)控制动态响应能力强, 但不能实现无静差追踪, 而重复控制能够进行无静差跟踪, 但存在延时问题且动态响应慢。将准PR控制与重复控制结合组成复合控制, 在实现无静差追踪的同时又具有良好的动态特性, 并分析了基于瞬时无功功率理论的ip-iq谐波检测。采用MATLAB/Simulink软件进行仿真, 结果表明该复合控制能够快速有效地抑制谐波。
关键词
光伏逆变器; 有源滤波器; 重复控制; PR控制
Abstract
Because photovoltaic inverter and active filter have the same topology, the combination of photovoltaic inverter and active filter is conducive to improving the efficiency of photovoltaic grid-connected.Quasi proportional resonance (PR) control has strong dynamic response capability, but it can not achieve tracking without static error, while repetitive control can achieve tracking without static error, but there is delay problem and slow dynamic response.In this paper, PR control and repetitive control are combined to form a composite control to control the photovoltaic inverter, and realize the grid connection and filtering functions at the same time. The ip-iq harmonic detection method based on instantaneous reactive power theory is emphatically analyzed and simulated by MATLAB/Simulink software. The final simulation results show that the compound control can effectively suppress harmonics.
Key words
photovoltaic inverter; active filter; repetitive control; PR control
“双碳”背景下, 我国大力推行发展新能源。随着光伏发电技术的成熟, 太阳能在新能源中的地位愈加重要。近年来, 大规模太阳能光伏并网给电网带来了极大的挑战, 并网过程产生的谐波严重损害输入电网的电能质量, 大大降低了光伏发电并网效率。电网中的谐波治理大多采用被动治理, 利用有源滤波器对系统中的谐波进行抑制。由于光伏逆变器与有源滤波器的拓扑结构类似, 因此将光伏逆变器与有源滤波器结合进行统一协调控制, 从源头上对电网谐波进行主动处理, 能够大大提高谐波治理效果, 提高电网电能质量。
对谐波进行准确有效的追踪以及控制补偿是谐波治理中的关键, 其中基于瞬时无功功率理论的ip-iq谐波检测法得到了广泛的应用。许多学者对谐波电流控制策略进行了研究: 文献[1]在同步旋转坐标系下采用了无差拍控制策略, 虽控制原理简单、响应速度特别快, 但该控制策略对建立的数学模型精确度要求较高, 计算较复杂, 存在一定的局限性; 文献[2]中采用的比例积分(Proportional Integral, PI)控制容易实现, 动态响应快, 但对于系统中的交流分量无法进行无静差跟踪; 文献[3]提出的准比例谐振(Proportional Resonant, PR)控制的抗干扰能力较差; 文献[4-6]中的重复控制虽然能够缩小系统的静态误差, 但存在周期延迟问题, 动态响应能力较差。
为了解决上述问题, 本文提出先利用基于瞬时无功功率理论的ip-iq谐波检测法对谐波进行准确检测, 然后结合准PR控制与重复控制的优点组成复合控制, 对系统中的谐波电流进行准确迅速补偿, 实现了光伏逆变器与有源滤波器的统一协调控制。最后, 通过仿真分析, 验证了该方法的有效性。
1 光伏并网系统
光伏并网系统主要包括光伏电池、最大功率点跟踪(Maximum Power Point Tracking, MPPT)模块、光伏逆变器、负载等模块。光伏并网系统统一协调控制示意如图 1所示。
图 1中, Sa1、Sb1、Sc1、Sa2、Sb2、Sc2是三相并网逆变器的内部拓扑结构的6个开关管; C1和C2为缓冲电容; Ipv和Upv分别为光伏阵列的输出电流和输出电压, Upv*为最大输出电压; Udc为直流侧电压, Udc*为基准值电压; La、Lb、Lc为三相滤波电感; Usa、Usb、Usc为三相并网电压。MPPT模块先对光伏阵列输出的最大功率进行跟踪, 使得光伏电池输出功率维持在最大值, 对通过PI控制得到有功电流指令ipv*、直流侧电压控制指令Δip以及负载侧谐波电流指令ih*进行指令合成, 得到电流跟踪指令i*, 最后运用准PR控制+重复控制对电流进行跟踪, 从而控制逆变器的输出电流, 并对电网电流进行谐波补偿。
2 谐波电流检测
谐波电流检测是光伏并网系统中的一个关键环节, 对非线性负载的谐波电流进行检测, 通过指令电流合成谐波电流补偿信号, 从而达到谐波补偿的作用。因此, 对谐波电流进行迅速、准确的检测能大大提高电网谐波补偿的效率和质量。
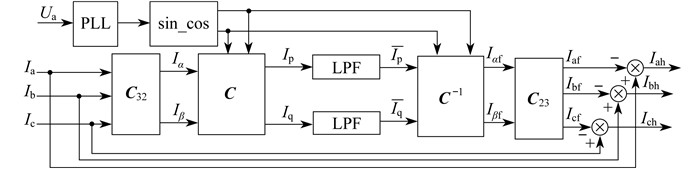
目前, 谐波电流检测的方法有许多种。文献[7]提出了一种基于FBD(Fryze-Buchholz-Dpenbrock)法的谐波检测法, 用于检测三相不平衡供电系统。文献[8]针对谐波检测方法中低通滤波器的延时问题, 提出了改进电流平均值法。文献[9]提出了一种基于瞬时无功功率理论的适用于三相电压不对称系统的改进p-q谐波检测法。其中, 基于瞬时无功功率理论的检测方法以其快速有效的特点得到了广泛应用, 具体包括p-q法和ip-iq法。基于瞬时无功功率理论的ip-iq检测法原理如图 2所示。
图 2中, Iα、Iβ为αβ坐标系下的两相瞬时电流, Iαf、Iβf为αβ坐标系下的基波电流, Iaf、Ibf、Icf为三相基波电流, Iah、Ibh、Ich为三相谐波电流, LPF表示低通滤波器。
锁相环(Phase Locked Loop, PLL)对电路输入的a相电压Ua进行锁相, 从而提取到与Ua同相位的信号sin_cos, 并将提取到的相位信号sin_cos添加到谐波检测电路中。三相电压和三相电流公式分别为
| $ \left\{\begin{array}{l} U_{\mathrm{a}}=\sqrt{2} E \sin \omega t \\ U_{\mathrm{b}}=\sqrt{2} E \sin \left(\omega t-\frac{2 \pi}{3}\right) \\ U_{\mathrm{c}}=U_{\mathrm{a}}=\sqrt{2} E \sin \left(\omega t-\frac{2 \pi}{3}\right) \end{array}\right. $ | (1) |
| $ \left\{\begin{array}{l} I_{\mathrm{a}}=\sum\limits_{n=1}^{\infty} \sqrt{2} I_n \sin \left(n \omega t+\varphi_n\right) \\ I_{\mathrm{b}} \sum\limits_{n=1}^{\infty} \sqrt{2} I_n \sin \left[n\left(\omega t-\frac{2 \pi}{3}\right)+\varphi_n\right] \\ I_{\mathrm{c}} \sum\limits_{n=1}^{\infty} \sqrt{2} I_n \sin \left[n\left(\omega t-\frac{2 \pi}{3}\right)+\varphi_n\right] \end{array}\right. $ | (2) |
式中: Ua、Ub、Uc——a相、b相、c相电压;
E——电压有效值;
ω——角频率;
Ia、Ib、Ic——a相、b相、c相电流;
In、φn——n次电流有效值和n次相位;
t——时间。
Ia、Ib、Ic经过转换得到Ip和Iq分量。
| $ \left[\begin{array}{c} I_p \\ I_q \end{array}\right]=\boldsymbol{C}\boldsymbol{C}_{32}\left[\begin{array}{c} I_{\mathrm{a}} \\ I_{\mathrm{b}} \\ I_{\mathrm{c}} \end{array}\right]=\left[\begin{array}{c} \sqrt{3} \sum\limits_{n=1}^{\infty} I_n \cos (n-1) \omega t-\varphi_n \\ -\sqrt{3} \sum\limits_{n=1}^{\infty} I_n \sin (n-1) \omega t-\varphi_n \end{array}\right] $ | (3) |
变换矩阵为
| $ \boldsymbol{C}=\left[\begin{array}{cc} \sin (\omega t) & -\cos (\omega t) \\ -\cos (\omega t) & -\sin (\omega t) \end{array}\right] $ | (4) |
坐标转换矩阵为
| $ \boldsymbol{C}_{32}=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \sqrt{3} & -\frac{\sqrt{3}}{2} \end{array}\right] $ | (5) |
坐标反变换矩阵为
| $ \boldsymbol{C}_{23}=\sqrt{\frac{2}{3}}\left[\begin{array}{cc} 1 & 0 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \end{array}\right] $ | (6) |
先通过CC32变换得到瞬时有功电流Ip和瞬时无功电流Iq, Ip和Iq经过低通滤波器滤波得到电流直流分量, 接着通过C-1C23变换得到基波信号Iaf、Ibf、Icf, 最后将三相电流减去基波电流得到谐波电流。
3 复合控制
3.1 准PR控制
准PR控制是在PR控制基础上的改进控制, 其控制器的传递函数GPR为
| $ G_{\mathrm{PR}}=K_{\mathrm{p}}+\frac{2 K_{\mathrm{r}} \omega_{\mathrm{c}} s}{s^2+2 \omega_{\mathrm{c}} s+\omega_0^2} $ | (7) |
式中: Kp——比例环节系数;
Kr——谐振因子;
ωc——截止角频率;
s——拉普拉斯算子;
ω0——谐振角频率。
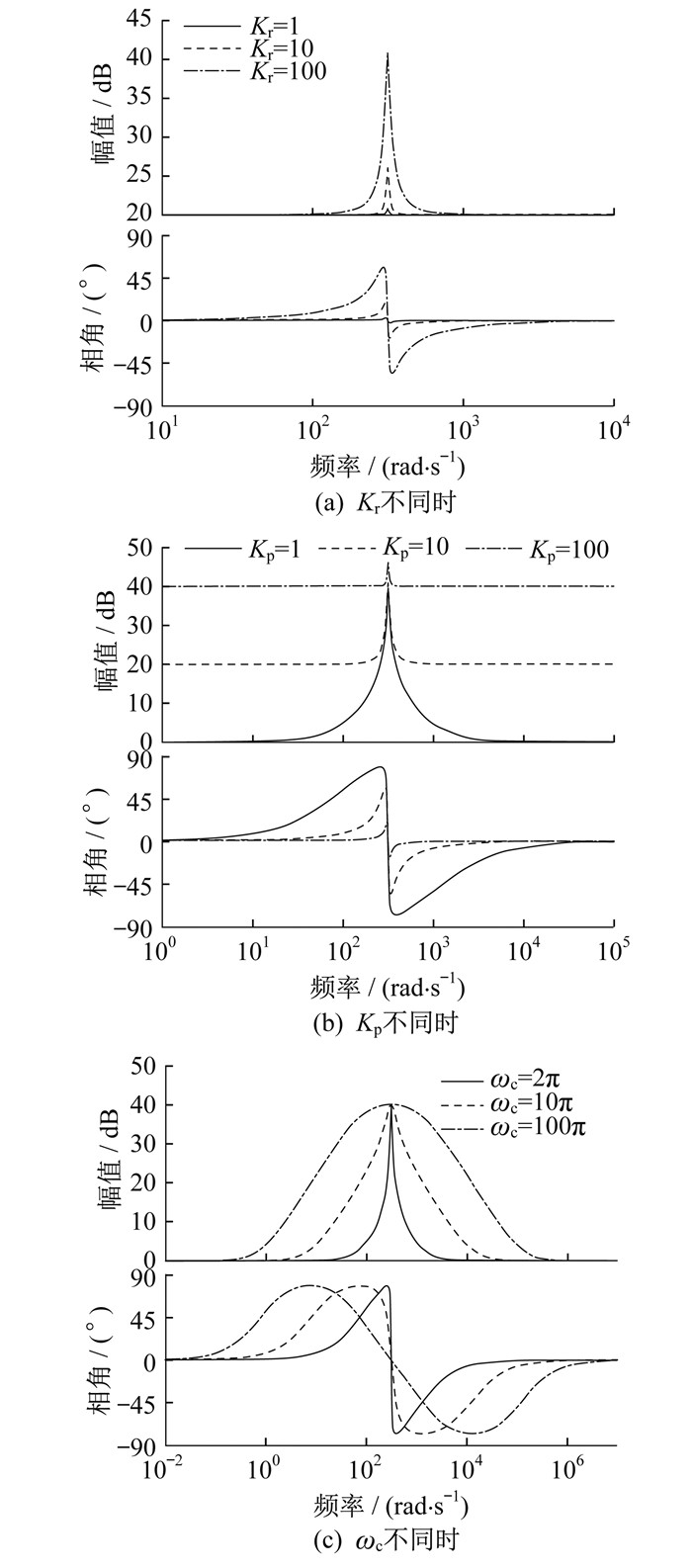
不同Kr、Kp、ωc时准PR控制的bode图如图 3所示。
图 3(a)中, 系统在基波频率处的增益随着Kr的增大而增大。由图 3(b)可以看出, 随着Kp的变化, 基波频率处的峰值基本不变, 而谐振带宽以外的幅值会变化, 整体曲线随着Kp的增大向上移动。图 3(c)中, ωc增大时, 系统在基波频率处的增益不会增大, 但两边的带宽明显增大。
因此, 为了保证系统的稳定性, 需要对准PR控制器中的Kr、KP和ωc进行合理取值。本文中取Kr=100, Kp=10, ωc=5。
3.2 传统的重复控制和改进的重复控制
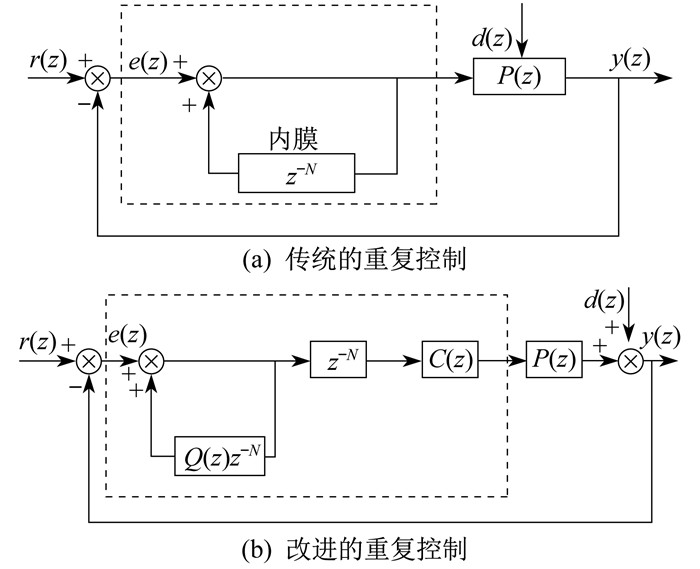
重复控制技术的核心思想是内膜原理, 将外部建立起的作用信号的数学模型植入控制器进行应用, 以构造一种高精度反馈结果的控制系统[9-10]。对传统的重复控制技术进行改进, 在内膜结构中用Q(z)z-N代替传统重复控制中的延迟环节z-N, 并增加补偿器C(z)模块, 增加了系统的稳定裕度, 使得系统稳定性更好。2种重复控制结构框图如图 4所示。
图 4中, r(z)、y(z)分别为系统输入参考信号和系统输出信号, e(z)为误差信号, 虚线框内为内膜结构, d(z)为外部周期扰动, P(z)为系统的控制对象。
补偿器C(z)可以对系统出现的幅值、相位的波动和偏差进行补偿。系统的闭环传递函数为
| $ \frac{y(z)}{r(z)}=\frac{z^{-N} C(z) P(z)}{1-z^{-N}[Q(z)-C(z) P(z)]} $ | (8) |
式中: Q(z)—衰减模块。
3.3 复合控制
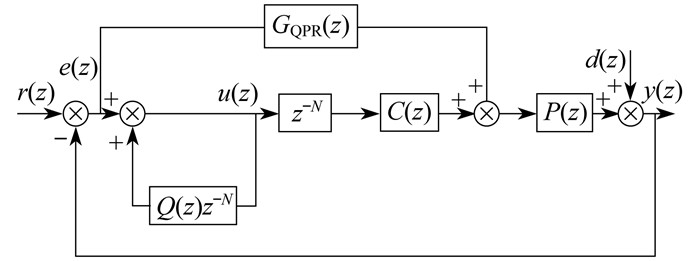
重复控制技术能够极大降低交流系统中的稳态跟踪误差, 对谐波抑制效果较好, 但其动态响应能力较差, 往往存在一个周期的延时问题[11-12]。准PR控制具有很好的动态响应能力, 因此将准PR控制与重复控制进行结合的复合控制能够兼顾两种控制的优点, 对系统中的交流分量进行快速稳定地无静差静态跟踪, 并且很好地抑制系统的谐波分量。复合控制结构框图如图 5所示。
图 5中, GQPR为准PR控制器。在复合控制结构中, 将准PR控制器当前时刻的输出与上周期同一时刻的误差结合作为调制信号控制复合控制的输出, 从而减小每个周期当前时刻的误差, 使其近似于零。当系统处于相对稳定状态时, 重复控制起主要作用, 完成对系统输出量的控制。当系统出现较大的扰动时, 由于准PR控制具有快速响应能力, 此时主要先由准PR控制控制系统, 重复控制经过一个周期延时过后发挥调节功能, 使系统恢复稳定状态。
3.4 参数设计
补偿器C(z)=KR·zk·S(z)是控制系统里最重要的环节。KR为增益系数, 通常取为1;zk为超前环节, 取为2。二阶低通滤波器S(z)主要是为了消除系统的高频干扰, 从而提高系统的稳定性[13]。若滤波器的截止频率设置过高, 则会使滤波器的滤波作用失去意义, 降低系统稳定性; 若设置过低则会抑制系统对高频谐波的输出, 降低对高频谐波的补偿能力。由于实际中滤波器主要是对25次以下的谐波进行补偿, 所以要求滤波器的截止频率不能低于25次谐波的频率。
取fc=2 kHz, 则滤波器C(z)为
| $ C(z)=\frac{0.391\ 3\left(z^2+2 z+1\right)}{z^2+0.365 z+0.195\ 8} $ | (9) |
4 仿真分析
运用MATLAB/Simulink软件进行建模仿真。主要仿真参数如下: 电源为三相电网220 V/50 Hz; 开关频率为10 kHz; 直流侧, Udc=600 V, 滤波电感为1.4 mH, 缓冲电容为1 mF; 负载端, 负载电阻为10 Ω, 负载电感为3 mH。
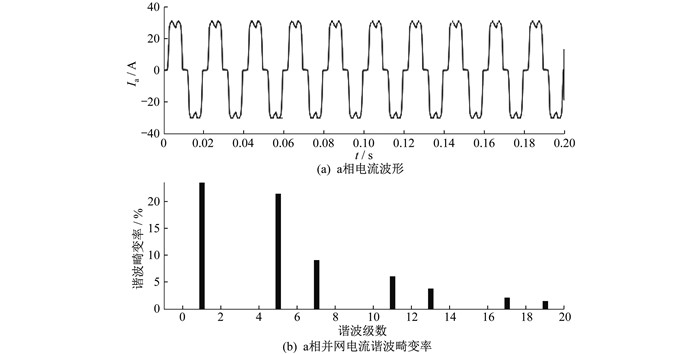
4.1 谐波检测模块仿真
4.2 统一协调控制仿真
传统的有源滤波器对谐波具有很好的抑制作用。虽然光伏并网逆变器与有源滤波器的工作原理不同, 但具有相同的拓扑结构和类似的控制策略[14]。因此, 将光伏并网逆变器与有源滤波器进行统一协调控制, 在晴天光照强度较大时, 系统通过指令电流跟踪和合成模块得到最终指令补偿电流信号, 并控制逆变器产生与最终指令电流相同或相似的电流注入电网, 提高并网的电能质量[15]。
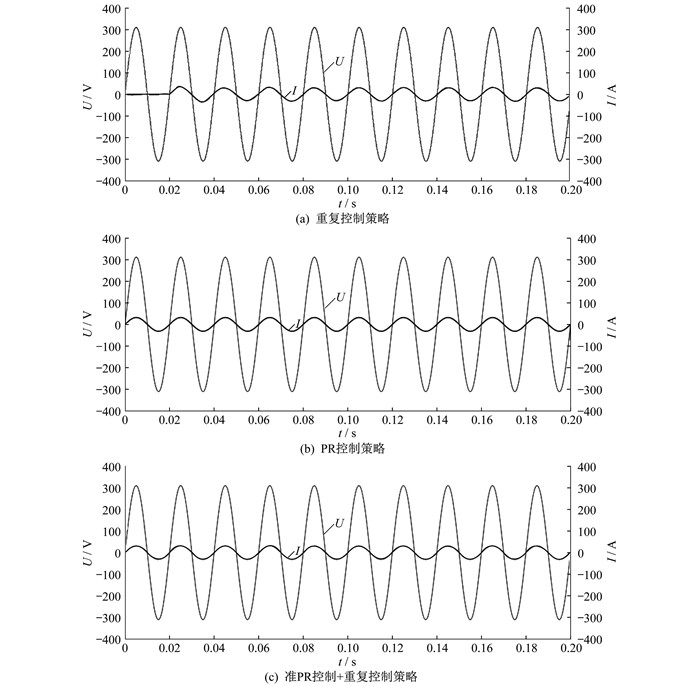
在重复控制、PR控制以及准PR控制+重复控制3种控制策略下, 电网电压U以及并网电流I仿真波形如图 7所示。由图 7可以看出, 在重复控制策略下, 能够一定程度地抑制谐波, 改善并网电流波形, 但往往存在一个周期的延时问题, 动态响应比较慢。与重复控制相比, PR控制的动态响应能力较好, 但得到的电流畸变比较严重。准PR控制+重复控制既能实现无静差跟踪, 动态响应速度快, 并且控制下的并网电流畸变比较小。
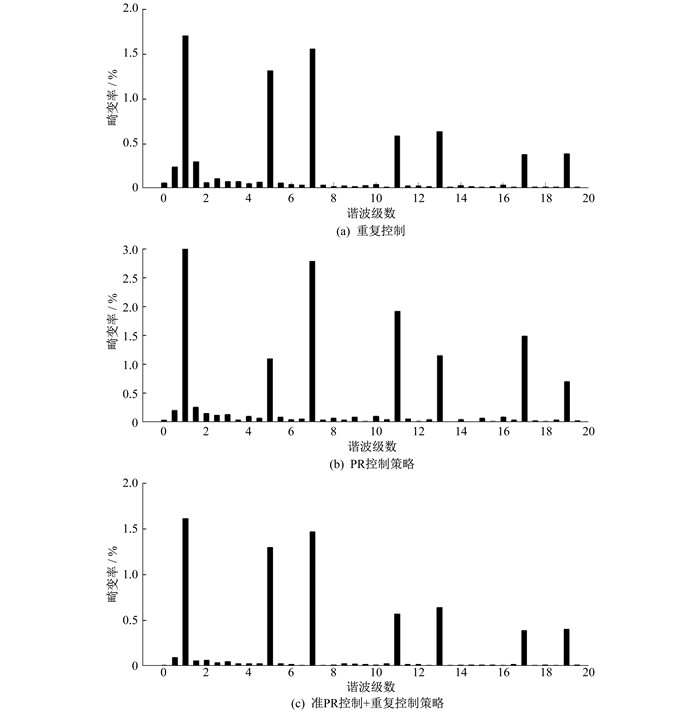
3种控制策略下并网电流的谐波畸变率如图 8所示。计算可得: 重复控制策略下, 电流波形的总谐波畸变率为2.32%, 对谐波具有一定的抑制作用; PR控制策略下, 电流波形的总谐波畸变率为4.65%;准PR控制+重复控制策略下, 电流波形的总谐波畸变率为1.92%。相比单独采用重复控制和PR控制时, 复合控制下的电流波形谐波含量明显减少, 并在响应速度和波形质量上均有明显提高。
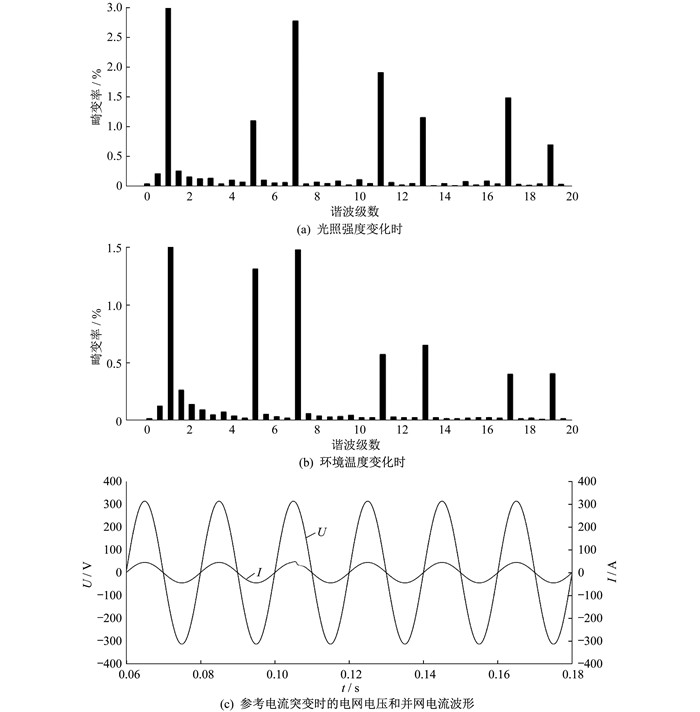
考虑到在实际应用中, 外界天气和环境温度可能发生变化, 因此对仿真条件作如下改变: 光照强度增加至1 500 W/m2, 环境温度提高至30 ℃。对应变化后, 统一协调控制下的并网电流谐波畸变率、电网电压和并网电流波形如图 9所示。
由图 9(a)和图 9(b)可知, 当光照强度和外界环境温度发生变化时, 并网电流和并网电压同频同相, 且并网电流波形的总谐波畸变率分别为3.01%和2.28%, 均小于5%, 符合并网要求。由图 9(c)可知, 在复合控制策略下, 当系统参考电流突变时, 经过0.01 s后, 并网电流波形恢复稳定, 这说明该控制策略具有很好的动态响应性。
5 结语
本文提出将光伏逆变器与有源逆变器进行协调统一控制, 采用基于瞬时无功功率理论的ip-iq谐波检测法对系统的谐波进行检测跟踪, 综合考虑PR控制和重复控制的优缺点, 将准PR控制与改进的重复控制组成复合控制策略对电网电流进行控制。在MATLAB/Simulink环境中分别对重复控制、PR控制以及复合控制策略进行仿真, 结果表明, 与采用单一的重复控制和PR控制相比, 本文提出的复合控制策略同时具有准PR控制动态响应好的优点, 以及重复控制有效抑制电网谐波的能力, 提高了并网电流波形的质量, 符合并网要求, 实现了光伏逆变器与有源滤波器的协调统一控制, 提高了电网的电能质量。
参考文献
-
[1]李英春, 南艳子, 张博, 等. 基于电流无差拍控制的单相光伏并网逆变器研究[J]. 电子器件, 2018, 41(1): 152-157.
-
[2]钱念书. 基于PI控制的单相光伏并网逆变器的仿真研究[J]. 广东电力, 2012, 25(12): 57-60.
-
[3]高文豪, 陈荣, 阚加荣, 等. 基于多谐振PR控制的并网逆变器相位补偿研究[J]. 计算机与数字工程, 2022, 50(9): 2119-2125.
-
[4]房俊龙, 甄景龙, 马文川, 等. 并联有源滤波器的改进重复控制策略研究[J]. 电力系统及其自动化学报, 2020, 32(2): 133-139.
-
[5]王攀攀, 晏夏瑜, 徐瑞东, 等. 基于重复+PI控制的LCL型并网逆变器仿真研究[J]. 实验室研究与探索, 2020, 39(5): 90-97.
-
[6]吴斌, 杨旭红. 基于改进遗传PI和重复控制的三相逆变器并网研究[J]. 电力科学与技术学报, 2021, 36(6): 151-156.
-
[7]张展, 杜诗扬, 冷全超, 等. 一种改进型FBD谐波及无功电流检测方法[J]. 电子测量技术, 2021, 44(10): 39-44.
-
[8]艾永乐, 许增渊, 李向前, 等. 基于ip-iq改进的谐波和有功电流检测研究[J]. 电子测量与仪器学报, 2018(2): 172-178.
-
[9]金涛, 刘思议. 一种基于瞬时无功功率的改进p-q谐波电流检测方法研究[J]. 福州大学学报(自然科学版), 2018, 46(1): 82-88.
-
[10]YANG Y, BLAABJERG F, WANG H, et al. Power control flexibilities for grid-connected multi-functional photovoltaic inverters[J]. IET Renewable Power Generation, 2016, 10(4): 504-513.
-
[11]郑海峰. 三相四线制三电平有源电力滤波器控制策略的研究[D]. 长春: 吉林大学, 2020.
-
[12]梁欢, 张琦, 唐雨, 等. 用于并网逆变器谐波抑制的重复控制策略研究[J]. 电力电子技术, 2022, 56(9): 5-7.
-
[13]汪洋, 陈权, 胡存刚. 基于PI+重复控制的三电平逆变器研究[J]. 电力电子技术, 2021, 55(7): 113-116.
-
[14]张杰, 郭晓霞, 赵威. 光伏并网与有源滤波统一控制系统的研究[J]. 现代电力, 2015, 32(1): 64-69.
-
[15]张坤, 罗文广. 电压型逆变器的重复控制与准比例谐振的双闭环控制研究[J]. 广西科技大学学报, 2022, 33(3): 22-28.