在可再生能源中, 风力发电是目前发展最快且最有潜力的发电方式。如何大规模利用风力发电并保持其安全、稳定是当前研究的热点^[1]。双馈感应发电机(Doubly-Fed Induction Generator, DFIG)也称双馈风力发电机, 因其具有有功无功解耦能力、变速恒频等优点, 目前在大型风电场中得到了广泛应用。我国风电呈现出明显的地域特征, 需要进行远距离高压输电。由于输电线路过长, 会出现线路的电感效应, 所以一般在输电线路上串联补偿电容以提高输电容量及输电效率。但线路串补技术可能使电网发生次同步振荡(Subsynchronous Oscillation, SSO)。DFIG的定子直接与电网相连, 电网的SSO极易干扰风电机组的正常运行, 可能会使风电机组发生故障, 因此研究DFIG的SSO及其抑制策略具有重要意义。

现有研究表明, SSO频率范围通常低于工频频率50 Hz。按照产生机理, SSO可分成3类: 次同步谐振、次同步扭矩相互作用和次同步控制相互作用(Sub-Synchronous Control Interaction, SSCI), 其中SSCI是由DFIG发电系统中的电力电子装置与串补线路之间相互影响引起的, 属于一种电气振荡, 振荡发散速度更快, 危害更大^[2]。在以DFIG为主的风电场当中, SSCI出现频次最高。

风电并网系统SSO抑制策略中, 按照作用位置的不同可分为机侧抑制法和网侧抑制法。机侧抑制法包括变流器控制策略优化和附加阻尼控制。文献[3]表明选择合适的控制参数可有效减少SSO的发生, 但改变变流器参数可能影响其原有的控制性能, 如减小转子侧内环比例系数会导致控制器的电流跟踪效果下降。文献[4]利用超前滞后补偿设计了一个阻尼控制器来抑制SSCI, 取得了良好的效果, 但其不具有普遍适应性。网侧抑制法包括改变电网运行方式和安装灵活交流输电系统(Flexible Alternating Current Transmission System, FACTS)装置。改变电网运行方式可以有效解决SSO条件, 如将部分或全部串补电容切除, 但会导致功率损失或功率输送能力下降。安装FACTS装置并附加阻尼控制也可以抑制SSO。现阶段国内外研究较多的主要有静止同步串联补偿器(Static Series Synchronous Compensator, SSSC)、静止无功补偿器(Static Var Compensator, SVC)、统一潮流控制器(Unified Power Flow Controller, UPFC)等设备。文献[5]基于SSSC设计了多模式阻尼控制器, 针对不同的振荡模式信号采用相应相位补偿, 从而使其提供的电气阻尼为正。文献[6]在风力发电机端口采用带电压调节的SVC动态提供无功功率。文献[7]使用UPFC增强了含风电电力系统的阻尼效果。但这些方法由于附加了电力电子装置, 使得控制复杂度和成本有所上升。

本文基于SSO采用了一种改进锁相控制技术, 以满足控制系统的锁相精度要求; 针对转子侧变流器优化控制策略, 在不改变原有控制策略的基础上, 采用准谐振控制器(Quasi Resonant Control, QRC), 嵌入到转子侧变流器(Rotor-Side Converter, RSC)内部的d轴、q轴控制通道中, 以跟踪次同步谐振分量, 从而抑制SSO对定子输出的影响。通过MATLAB/Simulink软件仿真, 验证所提方案的正确性和有效性。

DFIG风力发电系统主要由风机、齿轮、DFIG、背靠背变流器4部分组成。网侧变流器(Grid Side Converter, GSC)是靠网端的变换器, 而RSC连接电机转子端^[8]。控制系统是整个DFIG风力发电系统的核心, 由GSC和RSC组成。GSC维持直流母线电压的稳定, RSC给DFIG转子绕组提供交流励磁, 并解耦DFIG定子输出的有功功率和无功功率, 进而完成对DFIG运行的控制。由于GSC和RSC模型结构相似, 采用的控制方式基本类似, 因此本文主要介绍RSC的控制策略。

利用电路定理和坐标变换得到dq坐标系下的DFIG数学模型为

$ \begin{gathered} {\left[\begin{array}{c} \boldsymbol{u}_{\mathrm{s} d} \\ \boldsymbol{u}_{\mathrm{s} q} \\ \boldsymbol{u}_{\mathrm{r} d} \\ \boldsymbol{u}_{\mathrm{r} q} \end{array}\right]=\left[\begin{array}{cccc} R_{\mathrm{s}} & 0 & 0 & 0 \\ 0 & R_{\mathrm{s}} & 0 & 0 \\ 0 & 0 & R_{\mathrm{r}} & 0 \\ 0 & 0 & 0 & R_{\mathrm{r}} \end{array}\right]\left[\begin{array}{c} i_{\mathrm{s} d} \\ i_{\mathrm{s} q} \\ i_{\mathrm{r} d} \\ i_{\mathrm{r} q} \end{array}\right]+} \\ {\left[\begin{array}{cccc} p & -\omega_1 & 0 & 0 \\ \omega_1 & p & 0 & 0 \\ 0 & 0 & p & -\omega_{\mathrm{s}} \\ 0 & 0 & \omega_{\mathrm{s}} & p \end{array}\right]\left[\begin{array}{c} \psi_{\mathrm{s} d} \\ \psi_{\mathrm{s} q} \\ \psi_{\mathrm{r} d} \\ \psi_{\mathrm{r} q} \end{array}\right]} \end{gathered} $

(1)

式中: u_sd、u_sq、u_rd、u_rq——定子、转子电压d轴和q轴分量;

R_s、R_r——定子、转子电阻;

ω₁——定子同步旋转角速度;

i_sd、i_sq、i_rd、i_rq——定子、转子电流的d轴和q轴分量;

ψ_sd、ψ_sq——定子磁链的d轴和q轴分量;

ψ_rd、ψ_rq——转子磁链的d轴和q轴分量;

ω_s——dq坐标系相对于定子的电角速度;

p——微分算子。

RSC采用定子电压定向的矢量控制, 忽略定子电阻R_s, 定子电压定向于电网电压矢量, 为

$ \left\{\begin{array}{l} \boldsymbol{u}_{\mathrm{s} d}=\left|u_{\mathrm{s}}\right|=U_{\mathrm{s}} \approx-\omega_1 \psi_{\mathrm{s} q} \\ \boldsymbol{u}_{\mathrm{s} q}=0 \approx \omega_1 \psi_{\mathrm{s} d} \end{array}\right. $

(2)

当定子电压和转子电流表示定子侧输出有功功率和无功功率时, DFIG定子有功功率为

$ P_{\mathrm{s}}=-R_{\mathrm{s}}\left|\boldsymbol{i}_{\mathrm{s}}\right|^2+\frac{L_{\mathrm{m}}}{L_{\mathrm{s}}} \boldsymbol{U}_{\mathrm{s}} i_{\mathrm{r} d} $

(3)

式中: u_s、i_s——定子绕组电压、电流矢量;

L_m——dq坐标系下定子、转子绕组互感;

L_s——dq坐标系下定子绕组自感。

DFIG定子无功功率为

$ Q_{\mathrm{s}}=\frac{U_{\mathrm{s}}^2}{L_{\mathrm{s}} \omega_1}+\frac{L_{\mathrm{m}}}{L_{\mathrm{s}}} \boldsymbol{U}_{\mathrm{s}} i_{\mathrm{r} q} $

(4)

根据式(3)和(4)可知, DFIG定子侧实现了输出的P_s与Q_s解耦, 此时定子侧输出的有功功率P_s和无功功率Q_s通过控制转子d轴电流和q轴电流即可控制^[9]。

转子电压的矢量方程为

$ \left\{\begin{aligned} \boldsymbol{u}_{\mathrm{r} d}= & u_{\mathrm{r} d 1}+e_{\mathrm{r} d}=R_{\mathrm{r}} i_{\mathrm{r} d}+\sigma L_{\mathrm{r}} \frac{\mathrm{d} i_{\mathrm{r} d}}{\mathrm{~d} t}- \\ & \left(\omega_1-\omega_{\mathrm{r}}\right)\left(-\frac{L_{\mathrm{m}}}{\omega_1 L_{\mathrm{s}}} U_{\mathrm{s}}+\sigma L_{\mathrm{r}} i_{\mathrm{r} q}\right) \\ \boldsymbol{u}_{\mathrm{r} q}= & u_{\mathrm{r} q 1}+e_{\mathrm{r} q}=R_{\mathrm{r}} i_{\mathrm{r} q}+\sigma L_{\mathrm{r}} \frac{\mathrm{d} i_{\mathrm{r} q}}{\mathrm{~d} t}+ \\ & \left(\omega_1-\omega_{\mathrm{r}}\right) \sigma L_{\mathrm{r}} i_{\mathrm{r} d} \end{aligned}\right. $

(5)

式中: u_rd1、u_rq1——控制器调节输出的d轴和q轴参考电压;

e_rd、e_rq——交叉耦合项及电压前馈解耦项;

σ——电机漏磁系数;

ω_r——dq坐标系相对于转子的电角速度;

L_r——dq坐标系下转子绕组自感。

根据式(5)得到转子侧控制框图如图 1所示。其中, P_sperf、Q_sqerf分别为定子侧有功、无功的参考值; i_rperf、i_rqerf分别为PI控制器输出的转子侧d轴和q轴电流参考值; PLL为锁相环; SVPWM为空间矢量脉冲宽度调制; u_abc、i_abc分别为定子侧的三相abc电压、电流。

由图 1可知, 转子侧控制器RSC通常采用双闭环PI调节的矢量控制策略, 即电流环和功率环; 在d轴电网电压定向的情况下, 转子电流的d轴分量控制定子有功输出, q轴分量控制定子无功输出, 通过控制转子d轴和q轴电流即可分别控制定子侧输出的有功功率和无功功率。

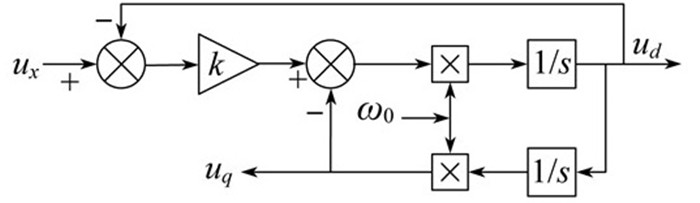
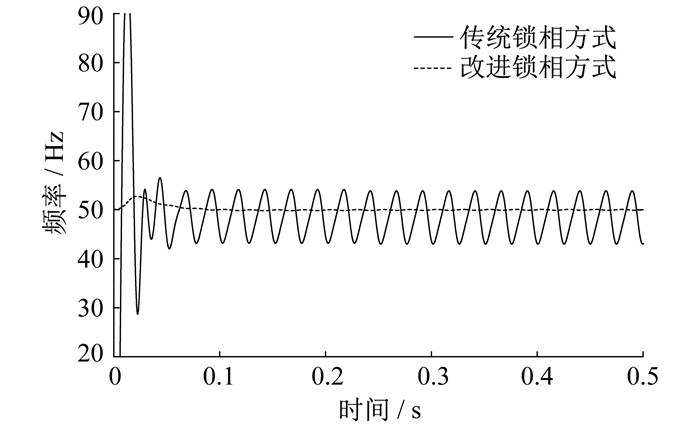
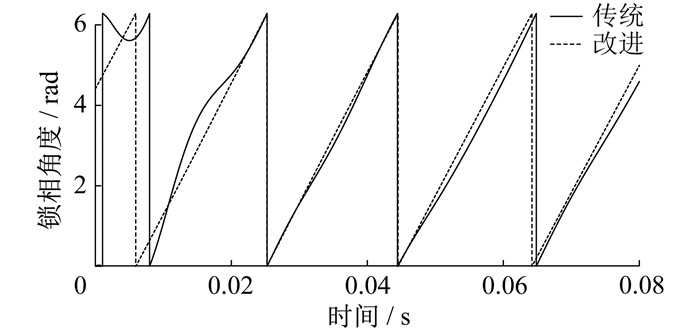
DFIG系统的基波分量在dq坐标系下为直流量, 在出现SSO的情况下, 次同步振荡分量表现为某个频率下的交流谐波。在电网次同步振荡情况下, 传统锁相方式锁得的电压频率会产生受次同步振荡频率影响的振荡, 无法满足控制系统的锁相精度要求。本文采用了一种基于2阶广义积分器(Second-Order Generalized Integrator, SOGI)的锁相控制方法, 将SSO时的基波正序分量先提取出来再进行锁相^[10]。非理想电网电压中提取出基波正序分量, 采用SOGI实现输入信号90°相移, 实现对某一给定正弦信号的无静差追踪, 其原理框图如图 2所示。其中, u_x为输入电压; k为阻尼比; ω₀为无阻尼自然频率; 1/s为积分环节; u_d、u_q为输出的d轴和q轴电压分量。

SOGI锁相环原理框图如图 3所示。其中, u_α、u_β分别为定子侧的三相abc电压u_abc的α轴和β轴分量; u_α⁺、u_β⁺分别为经过SOGI锁相后的u_α、u_β的正序分量; u_d⁺、u_q⁺分别为u_α、u_β经2s/2r变换后的d轴和q轴分量; ω_PLL、θ分别为锁相环PLL的角频率、相位。

由图 3可知, 在d轴电网电压定向的情况下, 通过坐标变换, 采用SOGI将SSO时的基波正序分量先提取出来, 再构造闭环使u_q=0以实现精确锁相。与传统的锁相控制相比, 在电网非理想情况下的SOGI锁相性能有了很大的改进, 能够在含有低次谐波及频率偏移情况下, 快速且正确地分离出正序基波分量。

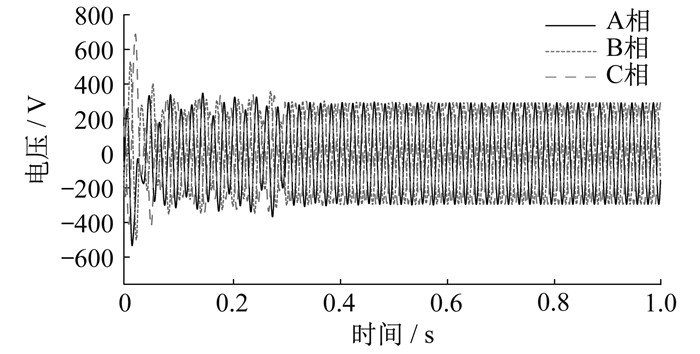
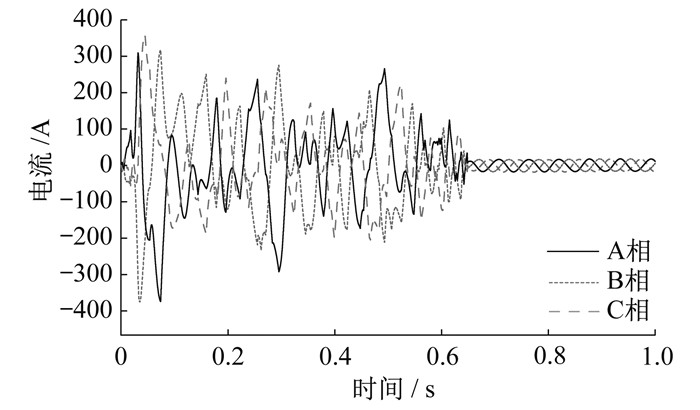
传统RSC控制策略为双环PI控制, 在电网中含有SSO分量时无法跟踪并抑制, 电网电流中的SSO分量会扩散。谐振控制器可以追踪交流信号, 利用此特征, 在理论上采用谐振控制器能够消除SSO分量的影响。因此, 通过改进RSC的控制策略以抑制次同步控制相互作用对发电机组的影响^[11]。

理想的谐振控制器又称为广义积分器, 能够对正弦信号实现无静差跟踪控制。在建模的过程中, 将谐振控制器与RSC原有的电流PI控制器相结合, 在达到RSC控制目标的基础上, 利用谐振控制器抑制次同步分量, 进而抑制SSO。

谐振环节对谐振频率正弦信号的幅值按照时间累积, 也就是积分的作用。本文采用的QRC的传递函数为

$ G_{\mathrm{R}}(s)=\frac{2 K_{\mathrm{R}} \omega_{\mathrm{c}} s}{s^2+2 \omega_{\mathrm{c}} s+\omega_0^2} $

(6)

式中: K_R——谐振系数;

ω₀——谐振角频率, rad/s;

ω_c——截止角频率, rad/s。

谐振环节能够对谐振角频率ω₀处的正弦信号进行幅值积分, 从而使谐振控制器对某一频率的正弦信号实现无静差跟踪^[12]。由SSCI振荡电磁过程分析可知, 当采用串联补偿电容的线路发生SSO, 定子同步旋转角速度为ω₁(ω₁=2πf₁, f₁=50 Hz), 次同步电流分量角频率为ω_n时, 在dq坐标系下表现为ω₁-ω_n角频率分量。若模拟实际情况下某一风电场发生了频率为15 Hz的SSO, 当电网存在15 Hz的SSO频率时, 经过坐标变换在dq坐标系下表现为35 Hz, 即转子谐振频率分量为35 Hz。

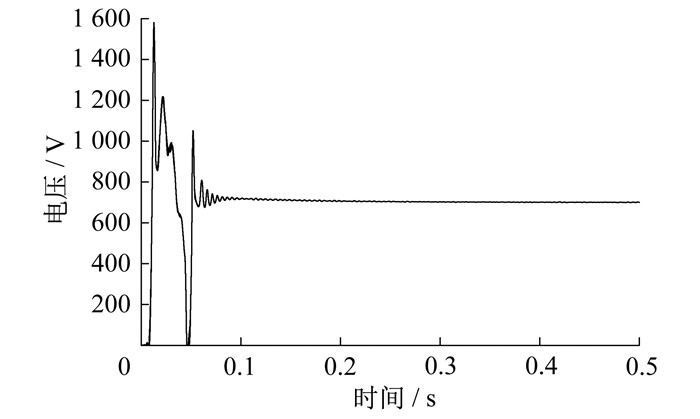
DFIG在理想状态下运行输出, 直流母线电压如图 4所示。

由图 4可知, 即使在启动时出现了一些波动, 直流母线电压仍然能够稳定在设定的700 V, 系统稳定运行。因此, GSC满足维持直流母线电压稳定的控制目标。

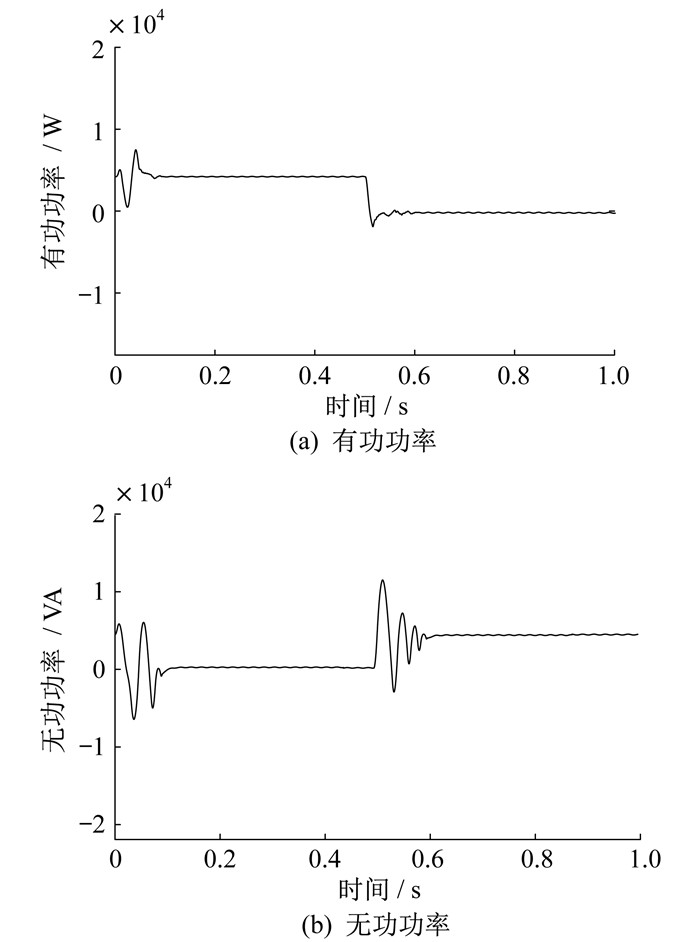
为验证RSC的控制目标, 即有功功率和无功功率的解耦能力, 设定阶跃指令使功率发生突变, 模拟实际DFIG运行环境条件发生变化时的情况。仿真中, 有功功率给定4 000 W, 无功功率给定0 VA, 设定时间为0.5 s时, 有功功率为0 W, 无功功率为4 000 VA。功率指令突变下有功功率和无功功率波形如图 5所示。

由图 5可知, 当输出功率指令阶跃响应发出突变时, 功率会产生一定的振荡, 但随后有功功率和无功功率都能够达到预期的0 W和4 000 VA, 可以跟随给定值。这表明通过转子侧d轴和q轴电流的控制可以将定子有功功率和无功功率解耦, 实现预期控制目标。

非理想电网条件即电网发生SSO时, 三相电压波形如图 6所示。

SSO下传统锁相方式与改进锁相方式的锁相频率对比、锁相角度对比如图 7和图 8所示。

由图 7可知, 在SSO工况下, 传统锁相方式锁得的频率产生振荡, 即存在SSO分量; 改进锁相方式虽然也有小幅振荡, 但整体维持在50 Hz, 锁相效果提升明显。由图 8可见, 传统锁相方式的锁相角度产生畸变, 而改进锁相方式不受影响。

在电网SSO工况下, 传统的RSC控制策略无法抑制SSO分量, 系统无法稳定。在0.3 s投入QRC, 图 9、图 10和图 11分别为QRC控制下三相定子电压波形、三相定子电流波形和定子有功功率波形。

由图 9、图 10、图 11可知, 在QRC作用下, SSO含量逐渐被抑制, 定子电压很快稳定, 定子电流和定子功率稍慢, 但均可以稳定。因此, 在SSO情况下, 采用基于RSC的QRC控制效果能够消除并抑制SSO。

本文对基于DFIG的SSO问题进行了研究, 推导出DFIG数学模型, 分析转子侧变流器的矢量控制策略, 对在理想电网条件下DFIG控制系统进行了仿真验证。在非理想电网电压情况下, 传统锁相方式无法达到控制系统的锁相精度要求。采用基于SOGI的改进锁相控制技术, 通过仿真对比两种锁相方式在SSO工况下的锁相效果, 验证了改进锁相控制的有效性。在改进了适应SSO频率的锁相技术后, 利用谐振控制器可以跟踪某一正弦信号的特性。采用QRC的次同步电流抑制策略, 并进行仿真验证, 证明加入QRC后能够抑制SSO分量, 从而使系统稳定。

后续可从以下方面进行深入研究: 对附加阻尼的抑制策略进行研究; 谐振控制的优点是参数整定简单、无需改变风机原有的控制策略、不用外加装置, 但缺点是只能针对单一的谐振频率进行控制, 在改变串补度后还需要调整参数, 无法自适应, 因此可以在谐振频率的提取及通过智能算法进行参数调整方面进行研究。