Print

发布时间: 2023-08-28
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2023.04.005
2023 | Volume 39 | Number 4




    新型电力系统    




  <<上一篇 




  下一篇>> 




分形理论在电力系统中的应用综述
expand article info 潘家华, 李宏仲
上海电力大学 电气工程学院, 上海 200090
收稿日期: 2023-03-11
中图法分类号: TM711
文献标识码: A
文章编号: 2096-8299(2023)03-0339-06

摘要

分形作为一种可利用自相似特性分析不规则对象的方法, 能够量化处理研究对象的几何特征, 进而更加直观地进行数据分析和规划。介绍了分形的定义及分类, 并分析了不同分形间的联系与区别。根据分形描述对象的性质差异, 从几何分形和代数分形两个角度综述了分形在电力系统不同领域中的应用现状, 并针对应用中面临的若干问题进行了分析。

关键词

分形; 电力系统; 非线性信号; 拓扑结构

An Application Review of Fractal Theory in Power System
expand article info PAN Jiahua, LI Hongzhong
School of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

As a method that utilizes the self-similarity property to analyze irregular objects, fractals can quantitatively process the geometric features of research objects, thereby making data analysis and planning more intuitive.This paper first introduces the definition and classification of fractals, and analyzes the connections and differences between different fractals.Then, based on the differences in the properties of objects described by fractals, from the perspectives of geometric fractals and algebraic fractals, the current application status of fractals in different fields of the power system is summarized, and several problems faced in application research are evaluated.Finally, the application of fractals in the power system is summarized.

Key words

fractal; power system; nonlinear signal; topology

随着高比例可再生能源的接入, 电力系统呈现出新的形式: 电力电量平衡概率化、灵活资源稀缺化、系统源荷界限模糊化、运行方式多元化、系统结构机理复杂化以及时间尺度多元化等[1]。面对大量随机性、非线性因素的耦合, 以及所呈现出的混沌和分岔特征, 如何利用合理的方法开展分析是新型电力系统理论研究所面临的重要问题之一。

20世纪80年代初, MANDELBROT B B[2]提出了分形理论(Fractal Theory)。它揭示了自然界中不规则事物的有序与无序、确定与随机之间对立统一的辩证关系。由于分形理论对非线性、非平稳性信号以及自然分形结构具有良好的处理能力, 因而在电力系统中得到了广泛的应用。在电力系统暂态信号中, 充斥着大量非线性元素[3-6]。相比于传统模型分析法, 分形能够深度挖掘这些非线性元素中蕴含的整体规律性, 进而提高电力系统分析决策的准确度。稳态信号的波动趋势分析通常是基于历史数据或量测数据进行的。然而, 随着电力系统数据逐步呈现高维化、复杂化, 该类信号的分析难度逐渐增大[7-9]。利用分形理论可以从海量数据中提取符合特定条件的部分, 进而大大提高信号波动特性分析的准确性。复杂网络拓扑是电力系统中典型的自然分形结构[10-11], 因此分形理论也适用于电力网络拓扑结构的分析与规划。

1 分形的定义及分类

分形是指一种具有自相似特性的图形、现象或物理过程等[2]。这种自相似性既可以体现在图形的外观特征上, 也可以体现在行为、方式、形态、功能、信息等特征上。对于现实系统而言, 自相似性是分形理论在多种场合成功应用的物理基础。

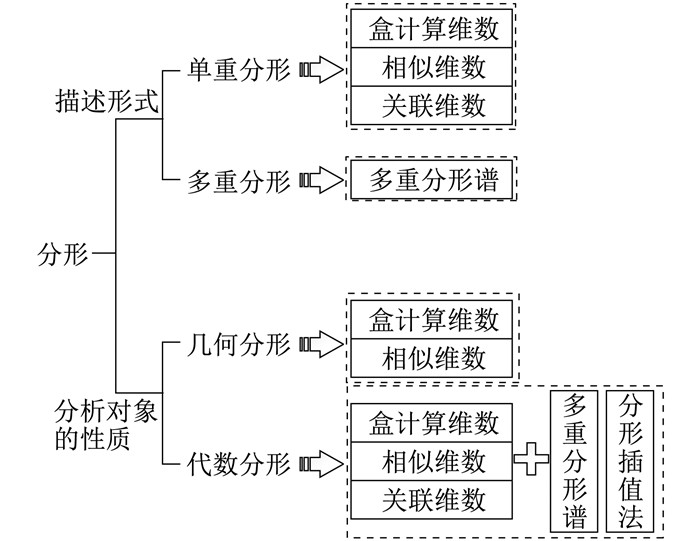
按照两种方式对分形进行分类, 具体如图 1所示。



图 1 分形的分类

根据描述形式的不同, 可分为单重分形和多重分形两类。根据分析对象的性质不同, 又可分为几何分形和代数分形两类。其中, 几何分形侧重于分析图形本身, 特别是具有分形特性的自然结构, 而代数分形则注重对数据序列曲线的分形特征开展量化分析。究其本质, 二者都是为了揭示不规则事物中所隐藏的整体与局部之间的自相似性。

(1) 单重分形  单重分形多用分形维数作为其表征量, 包括盒计算维数、相似维数及关联维数[2]。其中盒计算维数是最常见的一种分形维数计算方法。通常是利用覆盖分形图形表面的盒子尺度和数量之间的耦合关系来表示分形维数的大小, 适用于大部分具有分形特性的图形。相比之下, 相似维数的应用场合更为苛刻、单一。它主要用于描述具有强分形结构的图形, 反映研究对象的长度、体积或面积等与其直径之间的关系。与前两者不同, 关联维数是一种比较特殊的分形维数。它是在相空间重构理论[2]的基础上, 以时间序列数据为对象, 来研究其动力学特性的一种方法, 且在计算时需要重点考虑延迟时间和嵌入维数的取值。

(2) 多重分形  相对单重分形而言, 多重分形的结构更为复杂。它是由多个标度指数的奇异测度组成的集合[12-13], 可对不同分支上的分形测度变化进行细节描述[14-16], 不但避免了因仅考虑对象的整体特性导致信息丢失的情况, 而且还具有更好的抗噪声能力。多重分形谱作为多重分形的定量表征, 常用谱函数f(a)来描述不同层次的分形特征。即从小尺度出发, 根据自相似性研究最终整体特征。与盒计算维数类似, 它也可以利用测度理论进行定义[17-19], 即在同一个标度指数a下, 盒子数Na(r)和尺寸r之间的幂率关系为Na(r)~r－f(a)。

(3) 几何分形  几何分形作为最常见的分形类型, 主要用于分析具有分形特性的图形。这类图形在几何上具有很强的自相似性, 即整体与局部之间可以通过一定比例的缩放得到。为了能够准确地揭示这些复杂图形中存在的数学特征, 常利用盒维数和相似维数进行定量分析。

(4) 代数分形  研究发现, 一些混沌的、不规则的时序数据所构成的曲线在一定尺度下具有相似的波动趋势, 即所谓的自相似性。代数分形就是用于深度挖掘这些时序数据背后所隐藏的分形特性, 除盒计算维数法及相似维数法外, 代数分形还常用关联维数、多重分形谱以及分形插值进行分析处理。不同于前面几种方法, 分形插值法不仅能够描述不规则的随机曲线, 还能作为一种拟合经验数据的有效手段。通过对历史数据的分析, 完成未来一段时间的数据趋势预测。在实际应用中, 分形插值通常是利用迭代函数系和插值函数的组合来生成具有分形形状的图形。

2 几何分形在电力系统中的应用

几何分形在网络拓扑结构中的应用主要集中在两个方面: 一是改变拓扑结构类型, 进而利用分形寻找与决策变量之间的枢纽, 以反映拓扑结构变化所带来的影响; 二是根据复杂网络中节点度(用于描述不同度数节点的数量分布)存在一定幂率的特征, 利用分形研究其与网络拓扑之间的关联关系。

鉴于复杂网络中的拓扑结构具有自相似性的特点, 文献[20]利用盒维数法对链式、环网式和辐射式3种典型网架复合后的复杂网络结构进行量化处理, 构建了电网结构的分形维数与短路电流之间的数学关系, 实现了对网络拓扑的分区。随着研究的不断深入[21-22], 有学者发现节点度数为k的复杂网络中, 节点度分布P′(k)通常呈现出幂律分布的特征, 即P′(k)~k－γ, 且指数γ为常数。这就意味着网络的节点度分布在不同尺度下呈现出类似的形态, 即具有一定的自相似性。

有鉴于此, 文献[23]以节点度分布与网络的拓扑结构之间的联系为研究基础, 根据分形结构鲁棒性更好、脆弱性更低的特点, 利用最大边介数生成树的枢纽节点解耦策略[24]使得复杂网络拓扑更加“分形”化。

对于网络拓扑的分析, 几何分形主要是基于自相似性来研究拓扑结构的变化与决策变量之间的联系。随着电力网络复杂化程度加深, 一方面, 采样数据变得更加困难[25], 需要获取足够数量且均匀分布的数据样本, 以确保分形分析结果的准确性和可靠性; 另一方面, 系统中还充斥着大量随机噪声和干扰信号, 增大了分形特征的提取难度, 因此采用更加精细的算法和技术来提取特征值具有十分重要的现实意义。

3 代数分形在电力系统中的应用

3.1 暂态信号分析中的应用

电力系统中的暂态信号大部分是在故障中产生的, 具有突变性、非线性的特点。研究发现, 这些暂态信号在不同时间尺度下(一般为毫秒级)的时序数据有着相似的变化趋势, 即自相似特性[2]。因此, 可以利用分形维数、广义分形维数或分形谱对数据生成的整体或局部波动图形进行量化分析, 进而快速判断暂态信号的类型与发生位置。利用分形分析暂态信号的基本方法结构如图 2所示。



图 2 利用分形分析暂态信号的基本方法结构

3.1.1 输电线路故障分析

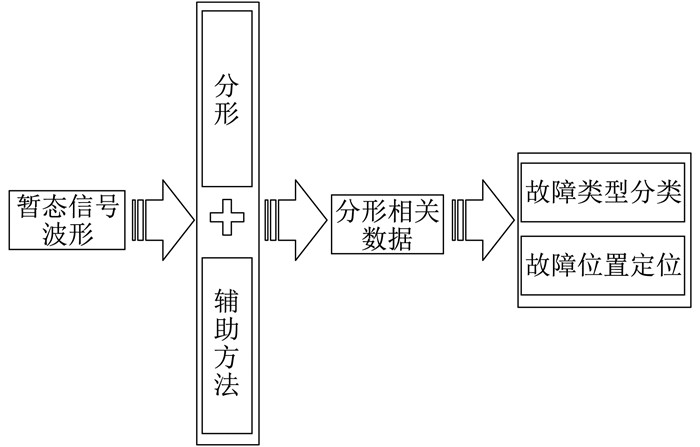
当输电线路发生故障时, 电路中会出现瞬时的电流和电压变化, 并且包含大量的暂态分量[26]。这些暂态信息间的差异性能够为故障诊断提供有力帮助[27]。当故障发生时, 健全线路与故障线路之间的电流信号波形存在一定差异[28-29], 可以利用分形维数来测定电流信号的波形特性, 将二者区分开来, 进而实现故障定位。

文献[30]以各相的故障电流为切入点, 利用模变换法将相电流转化为模电流, 并以故障前后各相模分量的分形维数差分值作为参考量, 将其与所设定的门槛值进行对比, 以判定故障类型。此方法能很好地解决弱电源侧的选相问题, 通过构建分形谱之间的关联参数, 更加细致地描述待测对象的特征。

为了进一步提高故障识别的准确率, 减少信息丢失, 需要对检测信号进行更加细致的局部处理[31-33]。文献[34]利用小波极大模法计算多重分形, 得到了故障线路和非故障线路信号的多重分形谱, 并通过分形谱图的变化趋势以及图形间的差异准确分辨出故障相。

为了有效改善S变换分析信号时的噪声干扰, 文献[35]在考虑多重分形的前提下, 将所提取的特征值和多重分形谱中的Hurst指数作为向量机的输入, 提高了信号识别的准确度。文献[36]利用多重分形去趋势波动分析法[37-39], 将最大、最小分形参数的比值与阈值的绝对值差作为参考量, 判断线路是否发生故障。

对于输电线路的故障检测, 单重分形能够利用分形维数开展量化分析, 使得非线性暂态信号的特征更加明显。多重分形能够更加细致地对局部变化趋势进行特征提取和信息融合, 进而大大提高结果的准确性。但电力系统中还存在大量不同属性的非结构性数据, 如何从海量数据中挖掘出所需的部分是代数分形适应新型电力系统分析应用的关键。

3.1.2 直流系统故障分析

直流系统的故障通常采用信号注入法进行检测。但由于其特殊的环网供电方式, 发生故障时会产生多个故障支路, 对故障判别造成了一定困难[40]。文献[41]利用小波变换法将采样的故障电流信号分解到不同的频带上, 并计算各个区间电流信号的分形维数。同时, 为了更加准确地描绘电流变化特征, 引入了故障电流信号表面的凹凸度参数。通过分形维数和凹凸度的结合分析, 提高了故障判断的准确性。文献[42]考虑到低频信号注入法在直流系统故障检测中的局限性, 利用多分辨率分析法提取环网电流信号低频段成分, 并计算电流信号曲线的分形维数大小, 有效实现了接地电阻变化下环网故障的判别。

在直流系统中, 不同类型的故障会导致电流或电压的分形维数发生不同的变化。通过分析不同类型故障的分形维数变化规律, 可以建立一套完整的故障诊断模型, 以实现对直流系统故障的准确诊断。但在实际应用中, 直流系统故障往往更加复杂化、多样化, 不同的故障可能会导致相似的分形特征, 就给故障诊断带来了一定的困难。因此, 在应用过程中应更注重数据采集和处理的相关技术。

3.1.3 电能质量扰动分析

随着大量非线性负载以及新型电力电子器件的投入, 电能质量扰动问题频发, 对电网运行的可靠性、经济性产生不利的影响。因此, 采用合理的方法进行电能质量扰动分析是维护电力系统安全运行与社会生活稳定的重中之重。文献[43]将小波分解法与盒计算维数相结合, 对不同故障类型扰动信号的分形维数进行分类, 并根据各个类别中的各相分形维数差异进行特征识别, 实现了从局部到整体对叠加的扰动信号的细致分类。文献[44]结合小波变换和差分维数, 将扰动信号分解到不同频带上进行时域分析, 并计算不同时间段的分形维数, 最后将所得的数据加入概率神经网络中进行分类, 但其并没有考虑扰动发生的时间。

对于电能质量的分析, 代数分形能够利用分形维数的大小和变化趋势对不同类型扰动信号进行准确区分和定位。然而随着新型电力系统的发展, 不断出现新的扰动因素[45], 因此提升分形对扰动信号的辨识能力至关重要。

3.2 稳态信号分析中的应用

在稳态信号分析中, 代数分形常用于分析负荷、电价等具有持续性、周期性及非线性特点的时间序列数据。与暂态信号相比, 这类时序数据的自相似性时间尺度更大, 通常为数小时到数天甚至更长。但这种相似性反映了电力系统中较为稳定的负荷和电价特性, 因此可以用于短期负荷预测[9]及电价波动评估[46]。

3.2.1 负荷预测

随着国民经济水平的不断提高, 对于电力的需求也在不断上升。用电负荷的波动会对电价造成一定的影响, 因此为了适应电力市场的要求, 有必要对负荷的预测评估进行深入研究。相关研究发现, 负荷的波动在每一个特定时间下的变化是无序的, 但在不同时间、相同尺度下的变化趋势是相似的, 即在大量无序的数据中存在一定的有序性。这就是电力系统负荷波动的分形特性[47-48]。

代数分形一般采用分形插值法对稳态信号进行处理。文献[49]利用分形理论的重标极差分析法挖掘负荷的持久性区间, 在选取相似日的基础上, 利用分形插值对待预测日进行预测。但其常用于内部函数的拟合, 对外部函数难以达到预测效果。文献[50]利用分形自相似性的特点, 将分形区间进行延拓。通过提前预实验, 将所得的结果与实际值相比较, 将误差最小的垂直尺度因子作为最优值, 进而开展负荷预测。该方法在一定程度上提高了负荷预测曲线的精确度。为了进一步避免主观因素对负荷预测的影响, 文献[51]以节假日负荷为主要研究对象, 考虑外在因素的影响, 通过拟合负荷与气象因子之间的耦合关系, 提高了整体负荷预测的精度。

在负荷预测的分析中, 分形主要通过建立模型来预测未来负荷变化。但电力负荷预测涉及到大量实时数据, 且这些数据在时间和空间上的分布十分不均匀, 即数据只会产生于特定的时间段, 就为分形模型的建立带来了一定的困难。因此, 应进一步提升数据插值法的可靠性。此外, 电力负荷数据往往受到许多因素的影响, 如季节性变化、天气变化等。这些因素会引入大量的噪声, 大大降低分形模型预测结果的准确性。因此, 应采用有效的方法去除电力负荷数据中的噪声。

3.2.2 电价波动评估

电价和负荷作为时间序列在一定程度上具有相似的性质。随着相关研究的不断深入, 电价的分形特征逐渐被挖掘出来[52]。文献[53]以加州电价数据为参考绘制分形谱图, 发现其波动具有多重分形特征, 且反映的复杂趋势与实际情况相同。但并没有进一步分析造成这种现象的原因。文献[54]以美国PJM 2001年和加州2000年电力市场的峰谷时段数据为研究对象, 利用标准多重分形、仿多重分形[55]、多重分形去趋势波动分析法对两者不同时段的波动情况进行分析, 并通过分形参数反映电价走势的混乱程度和持久性规律。

电价作为时间序列数据, 与负荷有着千丝万缕的联系, 但目前代数分形尚未将二者作耦合分析。可以考虑在计及电力市场行情、用户需求、天气等多种外在因素影响的前提下, 利用代数分形构建负荷和电价之间的关联参数, 并对电价实施分析, 进而制定合理的电价标准。

无论是对暂态信号还是稳态信号, 代数分形都能充分利用数据变化过程中的分形特性来完成对应的特征分析。但随着大量扰动因素的涌入, 有效信息丢失的情况变得尤为突出[56], 影响了实验结果的准确性。因此, 有必要进一步提升数据的提取和分类能力。

4 结语

分形作为一种研究非规则几何的新型学科, 其研究对象不仅仅是完全具有分形特性的几何图形, 还可以是在功能、信息、尺度上具有自相似特性的对象。目前, 分形在电力系统中的应用较广泛, 能够为故障检测和预测评估提供有力的帮助, 提高对非线性、复杂性对象研究的准确度。但随着电力系统的发展, 分形在数据处理方面存在的问题逐渐显现, 如对于数据量较大或分辨率较低的数据, 可能会产生较大的误差。因此, 为了推动分形在电力系统领域的应用, 可以对其在数据处理方面的问题作进一步的研究。

参考文献

  • [1]
    康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 1-10.
  • [2]
    朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011: 37-38.
  • [3]
    刘朋跃, 邵文权, 弓启明, 等. 利用零序电流相位变化特征的灵活接地系统故障选线方法[J]. 电网技术, 2022, 46(5): 1830-1837. DOI:10.13335/j.1000-3673.pst.2021.2055
  • [4]
    陈子璇, 席燕辉, 沈银. 基于卡尔曼滤波和深度置信网络的复合电能质量扰动分类[J]. 电力系统保护与控制, 2022, 50(7): 81-90.
  • [5]
    WANG Y, LI Q Z, ZHOU F L, et al. A new method with Hilbert transform and slip-SVD-based noise-suppression algorithm for noisy power quality monitoring[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(4): 987-1001. DOI:10.1109/TIM.2018.2864446
  • [6]
    YANG Z J, HUA H C, CAO J W. Multiple impact factor based accuracy analysis for power quality disturbance detection[J]. CSEE Journal of Power and Energy Systems, 2023, 9(1): 88-99.
  • [7]
    吕忠麟, 顾洁, 孟璐. 基于耦合特征与多任务学习的综合能源系统短期负荷预测[J]. 电力系统自动化, 2022, 46(11): 58-66.
  • [8]
    李滨, 陆明珍. 考虑实时气象耦合作用的地区电网短期负荷预测建模[J]. 电力系统自动化, 2020, 44(17): 60-68.
  • [9]
    刘倩倩, 刘钰山, 温烨婷, 等. 基于PCC-LSTM模型的短期负荷预测方法[J]. 北京航空航天大学学报, 2022, 48(12): 2529-2536. DOI:10.13700/j.bh.1001-5965.2021.0145
  • [10]
    汪家铭, 张静, 杨建华, 等. 基于广义短路比的多馈入直流系统受端电网结构优化方法[J]. 电力系统自动化, 2020, 44(24): 111-118.
  • [11]
    WANG Z, OH S K, KIM E H, et al. Hierarchically reorganized multi-layer fuzzy neural networks architecture driven with the aid of node selection strategies and structural network optimization[J]. IEEE Access, 2022, 10: 7772-7792. DOI:10.1109/ACCESS.2022.3140397
  • [12]
    WANG F W, WANG H, ZHOU X, et al. Adriving fatigue feature detection method based on multifractal theory[J]. IEEE Sensors Journal, 2022, 22(19): 19046-19059. DOI:10.1109/JSEN.2022.3201015
  • [13]
    KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E, et al. Multifractaldetrended fluctuation analysis of nonstationary time series[J]. Physica A: Statistical Mechanics and Its Applications, 2002, 316(1-4): 87-114. DOI:10.1016/S0378-4371(02)01383-3
  • [14]
    李舜酩, 李香莲. 振动信号的现代分析技术与应用[M]. 北京: 国防工业出版社, 2008: 224-277.
  • [15]
    DU W L, KANG M, PECHT M. Fault diagnosis using adaptive multifractal detrended fluctuation analysis[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 2272-2282. DOI:10.1109/TIE.2019.2892667
  • [16]
    LEON L, WENDT H, TOURNERET J Y, et al. A Bayesian framework for multivariate multifractal analysis[J]. IEEE Transactions on Signal Processing, 2022, 70: 3663-3675. DOI:10.1109/TSP.2022.3187196
  • [17]
    NIE Q, SHI K, GONG Y, et al. Spatial-temporal variability of land surface temperature spatial pattern: multifractal detrended fluctuation analysis[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 2010-2018. DOI:10.1109/JSTARS.2020.2990479
  • [18]
    FAN Y F, TAO M L, SU J. Multifractal correlation analysis of autoregressive spectrum-based feature learning for target detection within sea clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5108811.
  • [19]
    MAJI S K, THAKUR R K, YAHIA H M. Structure-preserving denoising of SAR images using multifractal feature analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2100-2104. DOI:10.1109/LGRS.2019.2963453
  • [20]
    李宏仲, 吕风磊, 范宏. 基于分形维数的500 kV/220 kV电网结构量化方法[J]. 电力系统自动化, 2015, 39(10): 87-92. DOI:10.7500/AEPS20140509011
  • [21]
    匡立. 分形网络的理论、算法及应用研究[D]. 武汉: 武汉大学, 2015.
  • [22]
    SONG C M, HAVLIN S, MAKSE H A. Self-similarity of complex networks[J]. Nature, 2005, 433: 392-395. DOI:10.1038/nature03248
  • [23]
    陈志鹏, 谢宁, 王承民, 等. 基于分形机理的复杂电力网络脆弱性评估及鲁棒性提升策略研究[J]. 电网技术, 2021, 45(2): 657-664.
  • [24]
    KIM J S, GOH K I, KAHNG B, et al. A box-covering algorithm for fractal scaling in scale-free network[J]. Chaos, 2007, 17(2): 026116. DOI:10.1063/1.2737827
  • [25]
    黎博, 陈民铀, 钟海旺, 等. 高比例可再生能源新型电力系统长期规划综述[J]. 中国电机工程学报, 2023, 43(2): 555-580.
  • [26]
    杜延辉. 多重分形和小波理论在小电流接地系统单相接地故障选线中的应用研究[D]. 成都: 西南交通大学, 2008.
  • [27]
    李东东, 周文磊, 郑晓霞, 等. 基于多重分形谱和支持向量机的风电机组行星齿轮箱故障诊断与研究[J]. 电力系统保护与控制, 2017, 45(11): 43-48.
  • [28]
    徐宁, 潘建兵, 李响, 等. 利用线路分形维数的配电网故障选线方法[J]. 电力系统及其自动化学报, 2018, 30(11): 140-146.
  • [29]
    孙雅明, 王俊丰. 基于分形理论的输电线路故障类型识别新方法[J]. 电力系统自动化, 2005, 29(12): 23-28.
  • [30]
    杨丹, 刘沛, 王冬青, 等. 基于分形理论的输电线路故障检测和选相[J]. 电力系统自动化, 2005, 29(15): 35-39.
  • [31]
    李小鹏, 丁宣文, 束洪春, 等. 基于多重分形谱的交流输电线路故障识别方法[J]. 电力系统保护与控制, 2021, 49(14): 1-10.
  • [32]
    ZHOU T J, LU J Z, LI B, et al. Fractal analysis of power grid faults and cross correlation for the faults and meteorological factors[J]. IEEE Access, 2020, 8: 79935-79946.
  • [33]
    PODOBNIK B, STANLEY H E. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series[J]. Physical Review Letters, 2008, 100(8): 084102.
  • [34]
    杜延辉, 张勤, 何岩, 等. 多重分形在小电流接地系统单相接地故障选线中的应用[J]. 继电器, 2008, 36(7): 10-14.
  • [35]
    杨秀, 张彤瑶, 潘爱强, 等. 基于S变换与多维分形的电压暂降源特征识别[J]. 电网技术, 2021, 45(2): 672-679.
  • [36]
    张宇辉, 王劼妍, 武东斌, 等. 基于多重分形降趋波动分析法的谐振接地系统故障选线新判据[J]. 电测与仪表, 2017, 54(20): 23-28.
  • [37]
    MOVAHED M S, JAFARI G R, GHASEMI F, et al. Multifractaldetrended fluctuation analysis of sunspot time series[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2(2): 02003.
  • [38]
    TANG J, WANG D B, FAN L, et al. Feature parameters extraction of GIS partial discharge signal with multifractal detrended fluctuation analysis[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(5): 3037-3045.
  • [39]
    ZHANG D M, WANG C, LI C Y, et al. Multi-fractal detrended fluctuation half-spectrum analysis of HRV[J]. The Journal of Engineering, 2019(22): 8315-8318.
  • [40]
    束洪春, 安娜, 董俊, 等. 高压直流输电线路故障识别的分形算法[J]. 电力系统自动化, 2012, 36(12): 49-54.
  • [41]
    李冬辉, 王金凤, 史临潼. 分形在直流系统故障检测中的应用[J]. 电力系统自动化, 2005, 29(21): 53-56.
  • [42]
    李冬辉, 李晟, 王金凤. 基于小波和分形的直流系统环网支路接地故障检测研究[J]. 继电器, 2006, 34(16): 17-21.
  • [43]
    王晶, 束洪春, 陈学允. 动态电能质量的分形指数小波分析方法[J]. 中国电机工程学报, 2004, 24(5): 40-45.
  • [44]
    胡为兵, 李开成. 基于小波与多维分形的电能质量扰动分类[J]. 继电器, 2008, 36(5): 45-48.
  • [45]
    韩肖清, 李廷钧, 张东霞, 等. 双碳目标下的新型电力系统规划新问题及关键技术[J]. 高电压技术, 2021, 47(9): 3036-3046.
  • [46]
    高原, 杨贺钧, 郭凯军, 等. 考虑负荷季节特性的电价型需求响应最优定价策略[J]. 电力建设, 2023, 44(1): 55-63.
  • [47]
    胡屏, 柏军, 兰华, 等. 基于分形理论的电力系统负荷几何特性研究[J]. 东北电力学院学报, 2002, 22(4): 48-52.
  • [48]
    刘映, 翟明岳, 刘永笑, 等. 一种改进的基于分形插值和小波分析的电力负荷短期预测方法[J]. 电网技术, 2013, 37(1): 276-280.
  • [49]
    李翔, 关勇, 乔艳芬. 基于分形理论的电力负荷持久性分析及预测[J]. 电网技术, 2006, 30(16): 84-88.
  • [50]
    薛万磊, 于继来. 分形外推插值算法在电力负荷预测中的应用[J]. 电网技术, 2006, 30(13): 49-54.
  • [51]
    李滨, 黄佳, 吴茵, 等. 基于分形特性修正气象相似日的节假日短期负荷预测方法[J]. 电网技术, 2017, 41(6): 1949-1955.
  • [52]
    肯尼思·法尔科内. 分形几何——数学基础及其应用[M]. 曾文曲, 刘世耀, 戴连贵, 译. 沈阳: 东北大学出版社, 2003: 327-340.
  • [53]
    陈伟, 周晓阳, 尚金成, 等. 竞争性电力市场中电价的多标度分形实证分析[J]. 电力系统自动化, 2007, 31(17): 31-34.
  • [54]
    王访, 尚金成. 基于多重分形理论的电力交易价格分时段特征分析[J]. 电力自动化设备, 2013, 33(1): 62-69.
  • [55]
    YANG J Y, YU Z G, ANH V. Clustering structures of large proteins using multifractal analyses based on a 6-letter model and hydrophobicity scale of amino acids[J]. Chaos, Solitons & Fractals, 2009, 40(2): 607-620.
  • [56]
    刘伟佳, 尚金成, 周文玮, 等. 基于多重分形理论的电力市场风险价值评估[J]. 电力系统自动化, 2013, 37(7): 48-54.