|
|
|
发布时间: 2023-08-28 |
新型电力系统 |
|
|
|
收稿日期: 2023-05-08
中图法分类号: TM715
文献标识码: A
文章编号: 2096-8299(2023)04-0345-08
|
摘要
针对分布式电源(DG)出力不稳定以及线路负荷波动大对电网造成的不利影响, 提出了一种计及合环约束的分布式电源与配电网联合优化模型。上层模型考虑线路拓扑重构, 对DG进行选址定容; 下层模型计及DG出力的时序特性, 动态调整线路拓扑, 进一步提升对于DG的接纳, 并且优化线路的运行。同时, 在重构的过程中考虑合环电流约束以确保方案的可行性, 并采用二阶锥松弛将原问题转换为混合整数二阶锥规划。最后, 在MATLAB环境下通过cplex求解器, 以IEEE33节点模型为例开展仿真分析, 验证了所提方法的有效性。
关键词
分布式电源; 配电网重构; 二阶锥松弛; 混合整数二阶锥规划; 优化运行
Abstract
Aiming at the adverse effects of unstable output of distributed generation (DG) and large line load fluctuation on the power grid, a combined optimization model considering the timing characteristics of DG is proposed.The upper level model considers line topology reconstruction and determines the location and capacity of DG.The lower level model takes into account the characteristics of DG output, dynamically adjusts the line topology, further improves the integration of DG and optimizes the operation of the line.At the same time, the loop current constraint is considered during the reconstruction process to ensure the feasibility of the scheme, and second-order cone relaxation is used to transform the original problem into mixed integer second order cone programming (MISOCP).Finally, the effectiveness of the proposed method is verified through simulation analysis using the IEEE33 node model by a cplex solver in the MATLAB environment.
Key words
distributed generation; distribution network reconstruction; second-order cone relaxation; mixed integer second-order cone programming; optimize operation
双碳战略提出以来, 大力发展可再生能源已成为一种趋势[1-2]。分布式电源(Distributed Generation, DG)作为可再生能源的重要组成部分, 其渗透率正在逐年提高, 但存在出力不稳定、消纳难等问题, 对配电网的冲击日益增强[3-4]。配电网作为输电和用电的中间环节, 对于供电可靠性及电能质量起到重要作用[5-6]。除了来自DG的冲击外, 配电网中还存在负荷分布不均衡、网损高等问题, 因此合理规划配电网, 有利于提高DG的消纳, 并优化线路的运行。
目前, 对于配电网规划问题的解决方案主要有以下两种: 一是对配电网络进行扩容, 如新建变电站、开关站等[7], 但这种方法成本很高, 并且许多城市用地紧张, 没有多余的空间进行扩容; 二是进行配电网重构[8], 通过改变联络开关的状态, 对线路的拓扑结构进行优化重构。
在主动配电网环境下, 拓扑结构因其可灵活调整的能力常被用于智能配电网的主动管理策略[9], 目前已有学者提出采用配电网重构的方式优化配电网的运行[10-11], 但在DG接入配置的问题上, 少有学者考虑网络重构[12-15]。文献[12]建立了双层规划模型, 迭代求解DG选址定容问题以及配电网最优拓扑问题; 文献[13]考虑了系统负荷增长的问题, 并将网络重构、DG选址定容作为应对该问题的手段; 文献[14]计及负荷时序特性, 建立了多场景下综合规划的模型。但以上模型均为基于传统人工智能算法求解的模型, 无法直接调用商业求解器, 也无法保证求解结果的全局最优性。文献[15]考虑动态重构, 并在选址定容模型中引入了虚拟支路电压, 但未计及运行过程中DG的时序特性, 也没有对合环电流进行校验, 难以保证运行的安全性以及结果的可行性。
基于以上研究, 本文提出了一种计及DG时序特性的双层优化模型, 通过二阶锥松弛技术转换为混合整数二阶锥规划(Mixed Integer Second - Order Cone Programming, MISOCP), 并调用cplex求解器进行求解。此外, 为避免产生不符合安全运行约束的不可行解, 本文提出了改进的合环电流约束模型, 当线路拓扑发生改变时对合环电流进行校验。
1 分布式电源与配电网联合优化模型
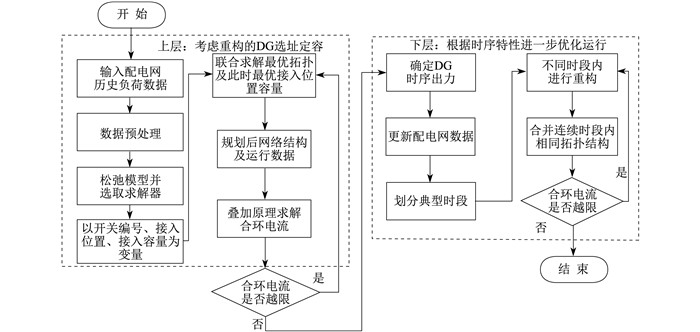
分布式电源与配电网联合优化模型是一个双层优化模型。上层模型为规划层, 考虑线路拓扑重构得到分布式电源的最优接入容量及位置; 下层为运行层, 在运行中以开关开合为变量, 进一步提升分布式电源的消纳。上下层模型的目标函数及约束条件相同, 求解变量不同, 下层模型以上层模型的结果作为输入, 计及分布式电源与负荷的时序特性, 联合求解最优的运行规划。
1.1 目标函数
目标函数主要基于线路网损、电压偏差和经济效益3个指标。其公式为
| $ \min W=\alpha P_{\text {loss }}+\beta \Delta U_{\Sigma}+\gamma C_{\mathrm{op}} $ | (1) |
式中: W——综合优化目标;
α、β、γ——网损、电压偏差量、开关动作成本的权重;
Ploss——线路网损;
ΔUΣ——电压偏差量;
Cop——开关动作成本。
线路网损公式为
| $ P_{\text {loss }}=\sum\limits_{t=1}^T \sum\limits_{n=1}^{N_{\text {line }}} R_{i j} I_{i j, t}^2 $ | (2) |
式中: T——一日中划分的时间段数, 取24;
Nline——线路的支路数;
Rij——支路ij上的电阻;
Iij, t——t时刻支路ij上流过的电流。
电压偏差量公式为
| $ \Delta U_{\Sigma}=\sum\limits_{t=1}^T \sum\limits_{i=1}^{N_{\mathrm{d}}}\left|U_{\mathrm{N}}-U_{i, t}\right| $ | (3) |
式中: Nd——线路的节点数;
UN——节点处的额定电压;
Ui, t——t时刻节点i处的电压。
开关动作成本公式为
| $ C_{\mathrm{op}}=\mu \sum\limits_{t=1}^T \sum\limits_{n=1}^{N_{\text {line }}} J_{i j} $ | (4) |
式中: μ——单次动作成本, 取7元/次[16];
Jij——支路ij开关动作计数, 若动作则取1, 否则取0。
1.2 约束条件
配电网重构的过程中需要满足以下5项约束。其中, 为确保可调用商业求解器进行求解, 对于非线性项采用文献[17]中的二阶锥形式。
(1) 节点功率平衡约束
| $ S_{\text {in }}=S_{\text {Load }}-S_{\mathrm{DG}} $ | (5) |
式中: Sin、SLoad、SDG——节点的注入视在功率、负荷视在功率和分布式电源视在功率。
(2) 节点电压约束
| $ \left\{\begin{array}{l} U_{\min }^2 \leqslant u_{i, t} \leqslant U_{\max }^2 \\ u_{j, t}=u_{i, t}-2\left(P_{i j, t} R_{i j}+Q_{i j, t} X_{i j}\right)+ \\ \ \ \ \ \ \quad\left(R_{i j}^2+X_{i j}^2\right) i_{i j, t} \\ u_{i, t}=U_{i, t}^2 \\ i_{i j, t}=I_{i j, t}^2 \end{array}\right. $ | (6) |
式中: Umin、Umax——系统允许的最低电压和最高电压;
ui, t、uj, t——过程变量, 数值等于t时刻节点i和节点j处电压的平方;
Pij, t、Qij, t——t时刻线路ij上传输的有功功率及无功功率;
Xij——线路ij上的电抗;
iij, t——过程变量, 数值上等于t时刻支路ij上电流的平方。
(3) 传输功率容量约束
| $ \left\{\begin{array}{l} P_{i j, t}=\sum\limits_{j \in i} r_{i j, t} G_{i j}+T_{i j, t} B_{i j} \leqslant P_{\max } \\ Q_{i j, t}=\sum\limits_{j \in i} T_{i j, t} G_{i j}-R_{i j, t} B_{i j} \leqslant Q_{\max } \\ r_{i j, t}=U_{i, t} U_{j, t} \cos \theta_{i j, t} \\ T_{i j, t}=U_{i, t} U_{j, t} \sin \theta_{i j, t} \end{array}\right. $ | (7) |
式中: rij, t、Tij, t——过程变量, 展现潮流约束的二阶锥形式, 无实际物理意义;
Gij、Bij——线路ij上的电导与电纳, 若两节点之间不存在物理拓扑关系时取0;
Pmax、Qmax——线路允许通过的有功、无功功率的最大值;
Uj, t——t时刻节点j处的电压;
θij, t——t时刻线路ij两端的电压相位差。
(4) 辐射状约束 配电网通常是闭环设计、开环运行, 在重构的过程中不允许出现环网或孤岛, 因此需要满足以下辐射状约束:
| $ \left\{\begin{array}{l} \sum\limits_{i j \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text {Line }}} F_{i j}=N_{\mathrm{d}}-N_{\text {root }} \\ \sum\limits_{i \in u(j)} F_{i j}=1, \forall j \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text {node }} \\ F_{i j} \in\{0, 1\}, \forall i j \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text {Line }} \end{array}\right. $ | (8) |
式中: ΦLine——系统各支路集合;
Fij——布尔变量, 取1时表示支路ij联通;
Nroot——线路的根节点数;
u(j)——节点j的父节点的集合;
Φnode——系统中除电源节点外其他节点的集合, 任意节点的父节点有且仅有1个。
(5) 开关动作约束
| $ \left\{\begin{array}{l} \sum\limits_{t=1}^T \sum\limits_{n=1}^{N_{\text {line }}} J_{i j} \leqslant N_{\mathrm{M}} \\ J_{i j} \leqslant N_{\mathrm{m}} \end{array}\right. $ | (9) |
式中: NM——每日开关动作总次数的上限;
Nm——单个开关每日动作次数的上限。
1.3 分布式电源时序模型
分布式电源的时序特性与配电网运行密切相关, 在上层优化模型确定好额定容量及接入位置后, 考虑风速及光照强度, 求得分布式电源的时序特性曲线, 并将其叠加至线路负荷进行下层优化。
(1) 风力发电机组出力模型 风速近似认为服从WeiBull分布[18], 其有功出力与风速的关系式[19]如下
| $ P_{\mathrm{w}}=\left\{\begin{array}{l} 0, \quad v_t \leqslant v_{\mathrm{i}} \text { 或 } v_t \geqslant v_0 \\ P_{\mathrm{N}} \frac{v_t-v_{\mathrm{i}}}{v_{\mathrm{N}}-v_{\mathrm{i}}}, \quad v_{\mathrm{i}}<v_t<v_{\mathrm{N}} \\ P_{\mathrm{N}}, \quad v_{\mathrm{N}}<v_t<v_0 \end{array}\right. $ | (10) |
式中: Pw、PN——风力发电机组实际有功功率与额定有功功率;
vt——t时刻风速;
vi、vN、v0——切入风速、额定风速及切出风速。
(2) 光伏电源出力模型 光照强度近似认为服从Beta分布[20], 其有功出力与光照强度关系式[21]如下
| $ P_{\mathrm{pv}}=n_{\mathrm{pv}} E_{\mathrm{LI}} A_{\mathrm{sur}} \eta $ | (11) |
式中: Ppv——光伏电源出力;
npv——光伏板数量;
ELI——光照强度;
Asur——光伏板面积;
η——光电转换效率。
1.4 双层优化模型的优化变量及求解方法
尽管上下层模型的目标函数及约束条件保持一致, 但优化变量完全不同, 上下层优化变量表达式分别如下
| $ \chi_{\mathrm{c}, 1}=\left\{x_{i, \text { loc }}, S_i \mid \chi_{\text {conf }, \text { opt }}\right\}, i \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text {node }} $ | (12) |
| $ \left\{\begin{array}{l} \chi_{\text {conf }, t}=\left\{F_{i j}\right\}, i j \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text {Line }} \\ F_{i j} \in\{0, 1\} \\ \left\|\chi_{\text {conf }}\right\|_1=5 \end{array}\right. $ | (13) |
式中: χc, l——上层模型优化变量;
xi, loc——分布式电源的接入位置;
Si——节点i处分布式电源的接入容量;
χconf, opt——上层模型定容时最优情况对应的拓扑结构;
χconf, t——t时刻下层模型的拓扑结构;
χconf——下层模型优化变量。
上述分布式电源与配电网联合优化模型的总体架构如图 1所示。
2 合环电流约束模型
为保证供电可靠性, 重构的过程中多采用合环的方式[22]。为避免产生不可行解, 本文提出了改进的合环电流约束模型。
2.1 合环电流计算
合环电流的计算采用基于戴维南等效定理的叠加法[23], 将网络分解成有源网络和无源网络两部分。其原理如图 2所示。
对于合环前的纯辐射网, 可通过潮流计算得到合环前的电流, 具体公式为
| $ I_{j, t}^2=\frac{P_{j, t}^2+Q_{j, t}^2}{U_{j, t}^2} $ | (14) |
式中: Ij, t、Pj, t、Qj, t——t时刻合环前节点j处注入的电流、有功及无功功率。
对于合环后的等效无源环网, 不考虑原有电源及负荷, 仅保留线路等值阻抗及合环前两端母线的电势差, 电流的计算公式为
| $ \boldsymbol{I}_{\mathrm{c}, j k}=\frac{\boldsymbol{U}_{j k, \Delta}}{\boldsymbol{Z}_{j k, \mathrm{eq}}} $ | (15) |
| $ \boldsymbol{I}_{j k, t}=\boldsymbol{I}_{j, t}+\boldsymbol{I}_{\mathrm{c}, j k} $ | (16) |
式中:Ic, jk——线路环流, 取节点j流向节点k为正方向;
Ujk, Δ——节点j和节点k之间的电压降;
Zjk, eq——戴维南等效定理求得的j、k点之间的等值阻抗;
Ijk, t——合环后节点j流向节点k的电流。
但式中Ujk, Δ、Zjk, eq均为向量形式的非线性项, 为避免模型非凸, 本文将对Ic, jk作出如下改进, 取过程变量如下
| $ \left\{\begin{array}{l} i_{\mathrm{c}, j k}=\boldsymbol{I}_{\mathrm{c}, j k}^2 \\ U_{j k, \mathrm{re}}=U_{j, \mathrm{re}}-U_{k, \mathrm{re}} \\ U_{j k, \mathrm{im}}=U_{j, \mathrm{im}}-U_{k, \mathrm{im}} \end{array}\right. $ | (17) |
式中: ic, jk——过程变量, 数值上等于线路jk环流的平方;
Ujk, re、Ujk, im——过程变量, 数值等于节点j和节点k之间电压实部之差和虚部之差;
Uj, re、Uk, re——节点j和节点k处电压的实部;
Uj, im、Uk, im——节点j和节点k处电压的虚部。
将式(15)转换为二阶锥形式, 即
| $ i_{\mathrm{c}, j k}=\frac{1}{R_{j k, \mathrm{eq}}^2+X_{j k, \mathrm{eq}}^2}\left(U_{j k, \mathrm{re}}^2+U_{j k, \mathrm{im}}^2\right) \leqslant I_{\mathrm{c}, \text { max }}^2 $ | (18) |
式中: Rjk, eq、Xjk, eq——戴维南等效定理求得的节点j和节点k点之间的等值电阻和电抗。
合环电流的最大瞬时值iM及最大有效值IM计算公式分别为
| $ i_{\mathrm{M}}=\left(1+\mathrm{e}^{-\frac{0.01}{T_{\mathrm{a}}}}\right) I_{\mathrm{c}}\\ $ | (19) |
| $ I_{\mathrm{M}}=\frac{I_{\mathrm{c}}}{\sqrt{2}} \sqrt{1+2 \mathrm{e}^{-\frac{0.02}{T_{\mathrm{a}}}}} $ | (20) |
式中: Ta——衰减时间常数。
2.2 合环电流约束
(1) 稳态约束合环重构后线路上任意时刻的电流应小于线路允许通过的最大电流, 即
| $ \boldsymbol{I}_{j k, t} \leqslant I_{\max } $ | (21) |
式中: Imax——合环后线路上允许流过的最大电流。
(2) 暂态约束 在合环操作中, 应保证线路的冲击电流可以躲过1段速断保护, 暂态电流的最大有效值躲过2段保护, 稳态电流应躲过3段的整定值, 可用公式表示为
| $ \left\{\begin{array}{l} i_{\mathrm{M}}<I_{\mathrm{set} 1} \\ I_{\mathrm{M}}<I_{\mathrm{set} 2} \\ I_{j k, t}<I_{\mathrm{set} 3} \end{array}\right. $ | (22) |
式中: Iset1、Iset2、Iset3——线路1段、2段、3段的继电保护整定值。
3 算例分析
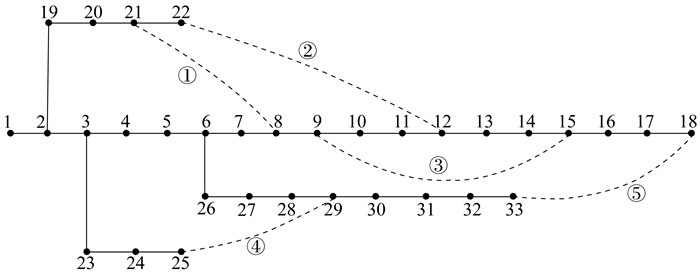
3.1 算例说明
3.2 不同优化方法结果对比
不同优化方法的结果对比如表 2所示。
表 2
不同优化方法结果对比
| 算例 | 全天网损/kWh | 电压偏差(p.u.) | 断开开关编号 | DG安装位置 | DG接入对应容量/MW | 合环电流校验 |
| 1 | 3 034.5 | 53.5 | 6、12、30 | 1.2、1.7、1.6 | ||
| 2 | 2 724.6 | 51.9 | 7、13、24 | 1.8、1.6、1.7 | ||
| 3 | 2 572.3 | 52.4 | 7、8、14、28、32 | 6、12、30 | 1.2、1.7、1.6 | 通过 |
| 4 | 2 203.8 | 48.6 | 9、12、28、32、33 | 7、14、30 | 1.8、1.2、2.0 | 通过 |
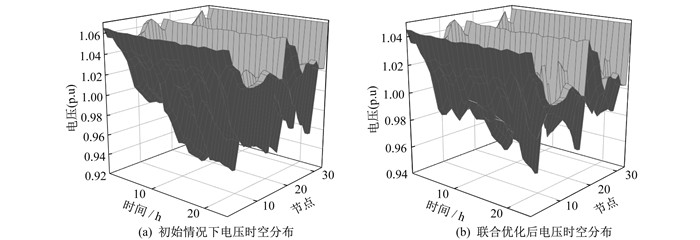
与初始情况算例1相比, 算例2和算例3的优化方法下网损分别降低了10.2%和15.2%, 算例4的联合优化方法下网损降低了27.4%, 优化效果更加明显。其优化前后的电压时空分布如图 4所示。由图 4可以看出, 联合优化后的电压分布更加紧致, 有效避免了分布式电源无序接入导致的电压越限等问题。因此可以得出结论, 联合优化方法可以更好地优化配电网的运行。
配电网重构的过程中需要进行2~10次合解环操作, 通过校验各次合解环电流的最大值可确保解的可行性以及过程的安全性。算例4的具体求解结果如表 3所示。此处选取中午12点进行校验, 仅保留每案例中合环稳态电流及冲击电流的最大值。
表 3
算例4求解结果
| 全天网损/ kWh | 电压偏差(p.u.) | 合环稳态电流最大值/A | 合环冲击电流最大值/A | 情形 | 合环电流校验 |
| 2 198.6 | 47.9 | 412.6 | 561.1 | 最优解 | 不通过 |
| 2 203.8 | 48.6 | 341.5 | 462.7 | 次优解 | 通过 |
| 2 245.4 | 49.7 | 321.6 | 407.7 | 第3次优解 | 通过 |
| 2 258.5 | 49.2 | 418.3 | 578.2 | 第4次优解 | 不通过 |
由表 3可以看出, 尽管合环冲击电流均小于线路继电保护的整定值, 但最优解及第4次优解的合环稳态电流越限, 会导致保护3段误动作。因此, 无法采取最优解, 退而求其次选择次优解。
3.3 多场景下运行优化验证
本文计及DG时序特性, 在算例4选址定容的基础上进一步优化配电网的运行。以春季的某个晴天工作日为例, 进行了动态重构且合并连续时段内相同拓扑后的详细结果如表 4所示。该日的平均风速光照强度参考文献[25], 天气、时间等影响因素参考文献[14]。
表 4
重构结果
| 重构时段 | 网损/kWh | 断开开关编号 | 开关动作次数 | 合环稳态电流最大值/A | 合环冲击电流最大值/A | 合环电流校验 |
| 0:00—08:00 | 410.1 | 7、9、28、32、34 | 16 | 279.6 | 397.1 | 通过 |
| 08:00—14:00 | 504.7 | 9、13、28、31、33 | 16 | 370.6 | 517.2 | 通过 |
| 14:00—17:00 | 254.6 | 11、28、32、33、34 | 16 | 437.2 | 601.9 | 不通过 |
| 17:00—24:00 | 471.2 | 7、9、28、31、34 | 16 | 387.4 | 577.3 | 通过 |
根据表 4中数据计算得出, 经过动态重构对配电网进行进一步优化后, 全天网损从2 203.8 kWh降至1 640.6 kWh, 降低了25.6%;对比初始网损3 034.5 kWh, 使用本文方法降低了45.9%。
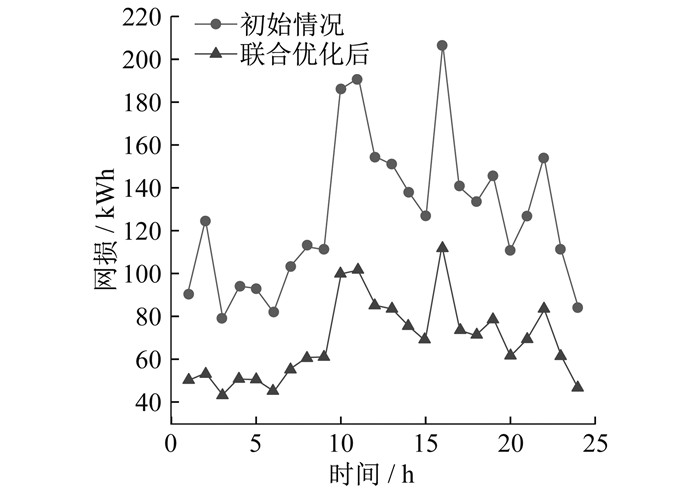
各时段的网损如图 5所示。
图 5中, 在时段14:00—17:00, 11#线路合环操作时的合环稳态电流越限。因此为保障安全性, 将校验时间调整为13:00或15:00。
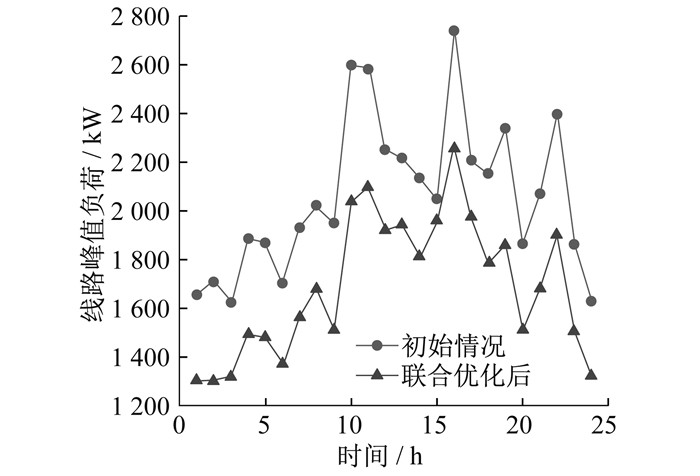
联合优化前后不同时段线路峰值负荷如图 6所示。
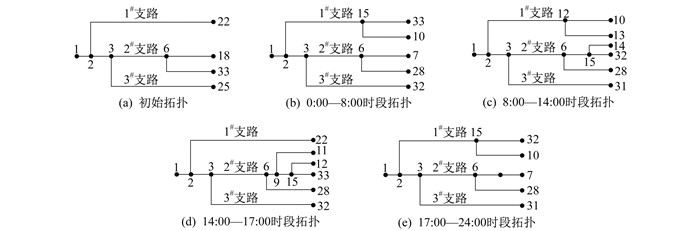
各时段减化拓扑如图 7所示。
与初始情况相比, 2#支路的部分负荷转移至1#、3#支路, 2#支路的峰值负荷由原来的2 740.7 kW降低至2 257.4 kW, 降低了约17.6%。这样可使得线路负荷更加均衡并挖掘出了扩容空间。
为保证所提方法的适用性, 在多情景下进行验证, 联合优化结果如表 5所示。
表 5
不同情景下的联合优化结果
| 情景 | 影响因素 | 网损/kWh | 开关动作次数/次 | 网损下降率/% | 电压偏差下降率/% | 线路峰值负荷下降率/% |
| 1 | 春季(晴天工作日) | 1 640.7 | 16 | 45.9 | 4.7 | 17.6 |
| 2 | 夏季(雨天工作日) | 1 829.6 | 20 | 41.8 | 5.6 | 14.8 |
| 3 | 秋季(晴天节假日) | 1 589.4 | 14 | 49.2 | 4.2 | 16.3 |
| 4 | 冬季(雪天节假日) | 1 752.5 | 16 | 43.4 | 4.8 | 15.5 |
4 结论
本文针对分布式电源与配电网联合优化的问题, 将分布式电源接入节点、接入容量及线路开关状态作为变量, 建立了多目标的联合优化模型; 并对约束进行二阶锥松弛处理, 调用cplex求解器对松弛后的模型进行求解。在IEEE33节点算例测试中得出如下结论。
(1) 在分布式电源建设规划时考虑拓扑重构可以明显提升对于新能源的接纳; 在配电网运行时随出力动态调整拓扑可以进一步优化配电网的运行。
(2) 针对合环电流越限的问题, 可以通过改变合环操作时间或采用次优解的方法进行规避, 在保证供电可靠性的前提下确保解的可行性以及过程的安全性。
(3) 在多情景下验证发现, 针对目前城市配电网扩容困难、分布式电源接入随机性强、出力不稳定等问题, 所提方案有一定的参考价值。
参考文献
-
[1]金国彬, 刘玉龙, 李国庆, 等. 考虑可靠性的交直流混合配电网网架与分布式电源协同优化规划[J]. 电力系统保护与控制, 2022, 50(22): 59-70.
-
[2]魏泓屹, 卓振宇, 张宁, 等. 中国电力系统碳达峰·碳中和转型路径优化与影响因素分析[J]. 电力系统自动化, 2022, 46(19): 1-12.
-
[3]杨扬, 王彤. 基于多目标双层规划的分布式电源选址定容[J/OL]. 华北电力大学学报(自然科学版): 1-12[2023-02-08].http://kns.cnki.net/kcms/detail/13.1212.TM.20220803.1152.002.html.
-
[4]吴成国, 肖仕武. 高比例分布式电源接入电网短路电流的拟牛顿迭代计算方法[J]. 电网技术, 2022, 46(12): 4581-4590.
-
[5]曹俊杰, 赵健, 单聚良, 等. 考虑合环约束的单双环配电网负荷重组均衡优化[J]. 电网技术, 2022, 46(9): 3604-3614.
-
[6]ZHAO J, XU M X, WANG X Y, et al. Data-driven based low-voltage distribution system transformer-customer relationship identification[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 2966-2977. DOI:10.1109/TPWRD.2021.3120625
-
[7]姚刚, 仲立军, 张代红. 复杂城市配电网网格化供电组网方式优化研究及实践[J]. 电网技术, 2014, 38(5): 1297-1301.
-
[8]LIU L, YU H T, LI L X. Distribution network reconfiguration based on harmony search/genetic hybrid algorithm[C]//2012 China International Conference on Electricity Distribution. Shanghai: IEEE, 2012: 1-4.
-
[9]余贻鑫, 栾文鹏. 智能电网述评[J]. 中国电机工程学报, 2009, 29(34): 1-8.
-
[10]唐早, 刘俊勇, 刘友波, 等. 空调聚合商参与下的负荷控制与配电网重构[J]. 电力系统自动化, 2018, 42(2): 42-49.
-
[11]江钧, 成乐祥, 孙国强, 等. 考虑安全域的配电网重构二阶锥双层规划模型[J]. 电力系统保护与控制, 2019, 47(4): 9-16.
-
[12]张沈习, 袁加妍, 程浩忠, 等. 主动配电网中考虑需求侧管理和网络重构的分布式电源规划方法[J]. 中国电机工程学报, 2016, 36(增刊): 1-9.
-
[13]ZIDAN A, SHAABAN M F, EL-SAADANY E F. Long-term multi-objective distribution network planning by DG allocation and feeders' reconfiguration[J]. Electric Power Systems Research, 2013, 105: 95-104.
-
[14]申洪涛, 岳凡丁, 史轮, 等. 考虑DG及负荷时序性的多目标配电网重构与DG调控综合优化规划[J]. 现代电力, 2022, 39(2): 182-192.
-
[15]朱俊澎, 顾伟, 张韩旦, 等. 考虑网络动态重构的分布式电源选址定容优化方法[J]. 电力系统自动化, 2018, 42(5): 111-119.
-
[16]李振坤, 路群, 符杨, 等. 有源配电网动态重构的状态分裂多目标动态规划算法[J]. 中国电机工程学报, 2019, 39(17): 5025-5036.
-
[17]JABR R A, SINGH R, PAL B C. Minimum loss network reconfiguration using mixed-integer convex programming[J]. IEEE Transactions on Power Systems, 2012, 27(2): 1106-1115.
-
[18]黄伟, 杨舒文, 葛良军. 基于概率潮流的主动配电网供需群体协同优化运行策略[J]. 电力系统自动化, 2017, 41(13): 39-44.
-
[19]倪识远, 张林垚. 考虑动态重构的主动配电网多目标双层优化调度方法[J]. 电力系统保护与控制, 2020, 48(20): 38-47.
-
[20]徐俊俊, 戴桂木, 吴在军, 等. 计及电动汽车和光伏不确定性的主动配电网量测优化配置[J]. 电力系统自动化, 2017, 41(1): 57-64.
-
[21]王敏, 宗炫君, 袁越, 等. 含光伏电站的发电系统可靠性分析[J]. 中国电机工程学报, 2013, 33(34): 42-49.
-
[22]武鹏, 程浩忠, 刘育权, 等. 考虑合环约束的配电网重构方法[J]. 电力系统自动化, 2017, 41(11): 163-168.
-
[23]周念成, 谷飞强, 雷超, 等. 考虑合环电流约束的主动配电网转供优化模型[J]. 电工技术学报, 2020, 35(15): 3281-3291.
-
[24]BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
-
[25]易海川, 张彼德, 王海颖, 等. 提高DG接纳能力的配电网动态重构方法[J]. 电网技术, 2016, 40(5): 1431-1436.