|
|
|
发布时间: 2023-10-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-07-10
基金项目: 国家自然科学基金(51977127)
中图法分类号: TM712
文献标识码: A
文章编号: 2096-8299(2023)05-0483-06
|
摘要
针对微电网物理层和信息层交互过程中存在虚假数据注入(FDI)攻击的情况, 提出了基于卡尔曼滤波的直流微电网抵御FDI攻击的二次控制策略。考虑常数FDI攻击和时变FDI攻击, 利用卡尔曼滤波器滤除二次控制中引入的攻击信号, 将经过滤波后的二次控制信号输入一次控制中, 实现恢复电压和精确分配功率的目的。通过2个仿真案例验证了所提方法的有效性。
关键词
微电网; 虚假数据注入攻击; 卡尔曼滤波算法; 二次控制
Abstract
Aiming at the situation of FDI attacks in the interaction between the physical layer and the information layer of microgrid, this paper proposes a secondary control strategy of DC microgrid to resist FDI attacks based on Kalman filter.The lead following consistency algorithm is used for secondary control.The Kalman filter is designed to filter out the attack signals introduced in the secondary control by considering constant attack and time varying attack signals.The filtered secondary control signal is input into the primary control to realize voltage recovery and power accurate distribution.Two simulation cases prove the effectiveness of the proposed method.
Key words
microgrid; false data injection attack; kalman filter algorithm; secondary control
在孤岛运行时, 微电网是一个独立自治的小型发配电系统, 能够利用良好的自我管控能力, 有效地优化、控制内部能量, 为重要负荷提供高质量的电能。传统的二次控制采用集中式的控制方法, 能够较好地实现对微电网内的能量管控。但面对数量巨大且地域分布广泛的分布式电源(Distributed Generation, DG), 集中式控制面临通信建设成本高、控制中心压力大、无法实现“即插即用”等问题[1-2]。因此, 分布式控制因其灵活性、可扩展性和更好的计算性能应运而生。
随着微电网采用的信息通信技术越来越开放和多元, 其受到网络攻击的风险也随之显著增加[3-5]。相比于集中式控制, 分布式控制缺乏掌握全局信息的能力, 无法利用集中式状态估计的方式对系统状态变量进行监控, 一旦受到网络攻击, 分布式控制将无法达到控制目标而失去其应有的作用。虚假数据注入(False Data Injection, FDI) 攻击广泛存在于信息层和物理层中, 并且该攻击方式难以检测, 容易造成巨大的危害[6]。因此, 研究FDI攻击下的微电网控制策略具有重要意义。
目前, 对于微电网中FDI攻击的解决方案主要包含两种: 一种是基于信息可信度的攻击抑制策略, 另一种是弹性控制策略。
对于基于信息可信度的攻击, 能在消除攻击信号的同时保证通信网络的连通性。文献[7]采用容错机制在控制器执行过程中逐渐减小攻击的扩散传播, 从而减小对微电网二次控制的影响, 但仅针对常数注入。为了抵御非常数注入攻击, 文献[8]设计了一种检测算法, 判断DG是否受到网络攻击, 并且通过更新通信邻接矩阵, 将受到网络攻击的DG从通信网络中边缘化甚至隔离。该方案虽然能够将网络攻击逐步隔离, 但是对受到攻击的代理数量有严格的限制, 而且可能会对稀疏通信网络的连通性和性能产生影响。
对于弹性控制策略, 文献[9]对二次控制器进行改进, 消除执行器上发生的注入值为常数的FDI攻击。对于发生在传感器及通信链路上的网络攻击, 文献[10-11]采用一种间歇性的控制策略, 通过4种不同通信模式的切换来抵御攻击。文献[12-13]则考虑了所有易受攻击的部位, 设置虚拟隐藏层与原有的通信层相连, 通过在隐藏层内处理信息从而避免网络攻击。虽然无需对DG进行隔离, 但新增的隐藏层提高了成本, 且一旦隐藏层受到网络攻击, 则系统将面临崩溃的风险。
为了消除攻击信号并降低成本, 本文提出基于卡尔曼滤波的直流微电网抵御FDI攻击二次控制策略。通过卡尔曼增益衡量测量值和估计值的可信度, 从而得到最优估计值, 消除攻击信号的影响。其中, 经二次控制处理的信息可直接输入一次控制中, 无需设置隐藏层。
1 直流微电网分布式控制系统
当直流微电网处于并网状态时, 大电网可以维持电压稳定, 但当微电网处于离网状态时, 由于没有大电网的支撑, 所以保持电压的稳定性就变得尤为重要。在分层控制中, 一次控制能够快速恢复电压和频率的稳定, 但会产生一定的偏差, 而该偏差需由二次控制予以消除[14]。
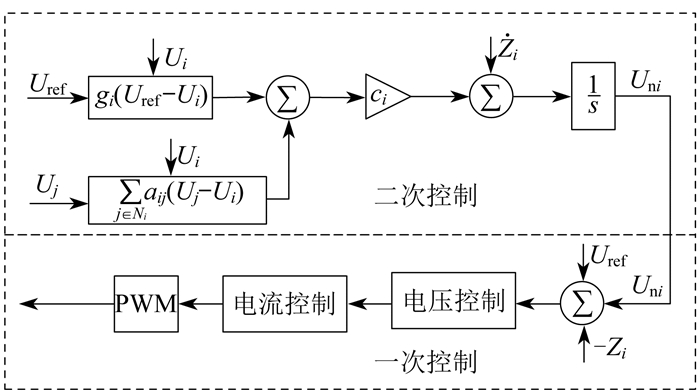
本文研究孤岛运行的直流微电网分布式控制, 其一次控制和二次控制的结构如图 1所示。其中: Uref为参考电压; gi为领导矩阵G=diag{gi}中的量; Ui为本地电压设定值; ci为一致性增益; Zi为虚拟阻抗;
1.1 直流微电网一次控制
一次控制中通常采用模拟一次调频的下垂控制策略。该策略通过调整下垂系数, 利用电压的偏移量实现电压和频率的有差调节。下垂控制是一种分散控制, 只需在本地进行而无需通信过程, 因此本文不做重点研究。
对于直流微电网, 其下垂控制特性可利用电压与功率间的关系来设定。当直流微电网电压升高时应降低电压, 反之则应升高电压。这一关系可表示为
| $ U_{i}=U_{\mathrm{ref} i}+U_{\mathrm{n} i}-Z_{i}$ | (1) |
式中: Urefi——系统电压参考值。
一次控制中还包括响应速度更快的电流控制环和电压控制环等控制环节。下垂控制的作用是为这两个控制环提供电压参考值, 电压控制环和电流控制环则负责控制输出期望波形。
1.2 直流微电网二次控制
在一次控制器的下垂控制设计中, 引入了二次电压修正量Uni。对式(1)求导可得:
| $ \dot{U}_{\mathrm{n} i}=\dot{U}_{i}+\dot{Z}_{i}=y_{i}$ | (2) |
式中:
yi——二次控制器输出量。
利用每个分布式电源的本地信息、邻居信息和参考电压信息设计二次控制器。其输出公式为
| $ y_{i}=c_{i}\left[g_{i}\left(U_{\mathrm{refi}}-U_{i}\right)+\sum\limits_{j \in N_{i}} a_{i j}\left(U_{j}-U_{i}\right)\right]$ | (3) |
式(3)中, 邻接矩阵A中aij表示DGi和DGj之间的连接关系, 若DGi与DGj之间有通信连接, 则aij=1, 反之则aij=0;领导矩阵G中gi表示DGi能否直接获得参考电压Uref, 若DGi能够直接获取Uref, 则gi=1, 反之则gi=0。
二次电压修正量Uni可由式(2)推导得到:
| $ U_{\mathrm{n} i}=\int\left(U_{i}+\dot{Z}_{i}\right) \mathrm{d} t$ | (4) |
式中: t——时间。
2 基于卡尔曼滤波的攻击抵御策略
2.1 攻击建模
考虑整个系统是在通信链路被FDI攻击后建立的, 此时二次控制器的输出公式为
| $ y_{i}^{\mathrm{F}}=c_{i} g_{i}\left(U_{\mathrm{refi}}-U_{i}^{\mathrm{F}}\right)+\sum\limits_{j \in N_{i}} a_{i j}\left(U_{j}^{\mathrm{F}}-U_{i}^{\mathrm{F}}\right)+\delta_{\mathrm{u}_{i}}$ | (5) |
式中: yiF——FDI攻击后二次控制器的输出量;
UiF、UjF——DGi和DGj受到FDI攻击时的电压值;
δui——经通信链路直接传递到控制器的攻击值。
式(5)可以进一步表述为
| $ \begin{gathered} y_{i}^{\mathrm{F}}=c_{i}\left[g_{i}\left(U_{\mathrm{ref} i}-U_{i}^{\mathrm{F}}\right)+\sum\limits_{j \in N_{i}} a_{i j}\left(U_{j}^{\mathrm{F}}-U_{i}^{\mathrm{F}}\right)\right]+\delta_{\mathrm{u}_{i}}= \\ c_{i}\left\{g_{i} U_{\mathrm{ref} i}-\left[\left(d_{i}+g_{i}\right) U_{i}-\sum\limits_{j \in N_{i}} a_{i j} U_{j}\right]\right\}+ \\ c_{i}\left[\sum\limits_{j \in N_{i}} a_{i j} \delta_{\mathrm{V}_{j}}-\left(d_{i}+g_{i}\right) \delta_{\mathrm{V}_{i}}\right]+\delta_{\mathrm{u}_{i}} \end{gathered}$ | (6) |
式中: δVi、δVj——攻击信号;
di——入度矩阵D=diag{di}中的量。
因此, FDI攻击信号分为两部分: 一部分为
| $ y_{i}^{\mathrm{F}}=c_{i}\left\{g_{i} U_{\mathrm{ref} i}-\left[\left(d_{i}+g_{i}\right) U_{i}-\sum\limits_{j \in N_{i}} a_{i j} U_{j}\right]+\delta_{\omega i}\right\}+\delta_{\mathrm{u} i}$ | (7) |
定义YF=[y1F, y2F, y3F, …, yNF]T, U=[U1, U2, U3, …, UN]T, Uref=[Uref1, Uref2, Uref3, …, UrefN], m×m的测量矩阵C=diag(ci), δω=[δω1, δω2, δω3, …, δωN]T, δu=[δu1, δu2, δu3, …, δuN]T, 然后将式(7)转换为全局形式的公式为
| $ \boldsymbol{Y}^{\mathrm{F}}=\boldsymbol{C}\left[\boldsymbol{G} \boldsymbol{U}_{\mathrm{ref}}-(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}+\boldsymbol{\delta}_{\omega}\right]+\boldsymbol{\delta}_{\mathrm{u}}$ | (8) |
式中: L——拉普拉斯矩阵。
由于本文采用一致性原则, 最终目的是使电压收敛于额定值, 使Uref1=Uref2=…=UrefN, 则L=D-A。将式(8)离散化, 变换为线性定常离散系统, 相应变量经过k次迭代后得到
| $\left\{\begin{array}{l}\boldsymbol{U}(k+1)=-(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}(k)+\boldsymbol{G} \boldsymbol{U}_{\mathrm{ref}}(k)+\boldsymbol{\delta}_{\omega}(k) \\ \boldsymbol{Y}(k+1)=\boldsymbol{C} \boldsymbol{U}(k)+\boldsymbol{\delta}_{\mathrm{u}}(k)\end{array}\right.$ | (9) |
式中: -(L+G)——n×n的系统矩阵;
Y——观测变量。
至此, 将二次控制中的FDI攻击问题转化为卡尔曼滤波问题。
2.2 攻击抵御策略
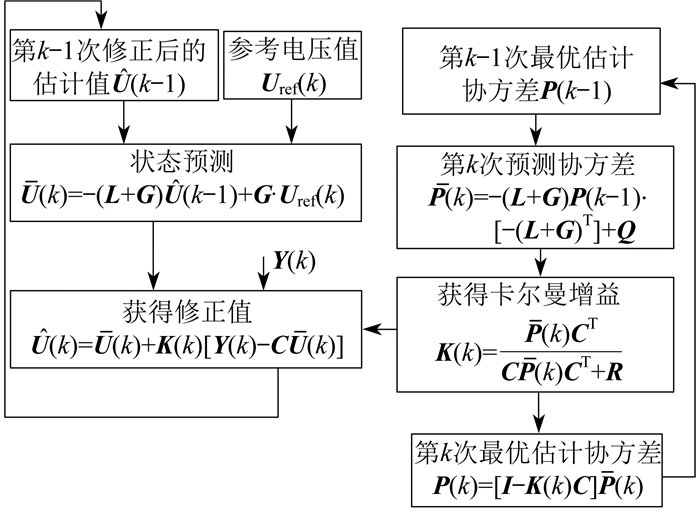
整个卡尔曼滤波过程如图 2所示。
为了使二次控制的输出不受FDI攻击信号的影响, 应将二次控制的最优估计值与受到攻击后二次控制的输出量之间的偏差最小化, 即最优估计协方差P(k)达到最小[15]。
利用本时刻的预测值U(k), 通过调整卡尔曼滤波增益K(k)来获得本时刻的估计值
| $ \hat{\boldsymbol{U}}(k)=\overline{\boldsymbol{U}}(k)+\boldsymbol{K}(k)[\boldsymbol{Y}(k)-\boldsymbol{C} \overline{\boldsymbol{U}}(k)]$ | (10) |
本时刻的预测值利用上一时刻的最优估计值
| $ \overline{\boldsymbol{U}}(k)=-(\boldsymbol{L}+\boldsymbol{G}) \hat{\boldsymbol{U}}(k-1)+\boldsymbol{G} \boldsymbol{U}_{\mathrm{ref}}(k)$ | (11) |
后验估计误差协方差为最优估计与真实值的误差, 本文记e(k)=U(k)-
| $ \begin{array}{l} \boldsymbol{e}(k)=\boldsymbol{U}(k)-\{\overline{\boldsymbol{U}}(k)+\boldsymbol{K}(k) \cdot\\ \left.\left[\boldsymbol{C U}(k)+\boldsymbol{\delta}_{\mathrm{u}}(k)-\boldsymbol{C} \overline{\boldsymbol{U}}(k)\right]\right\} \end{array}$ | (12) |
于是
| $ \begin{gathered} \boldsymbol{P}(k)=E\left[\boldsymbol{e}(k) \boldsymbol{e}^{\mathrm{T}}(k)\right]=[\boldsymbol{I}-\boldsymbol{K}(k) \boldsymbol{C}] \cdot \\ \overline{\boldsymbol{P}}(k)[\boldsymbol{I}-\boldsymbol{K}(k) \boldsymbol{C}]^{\mathrm{T}}+\boldsymbol{K}(k) \boldsymbol{R} \boldsymbol{K}(k)^{\mathrm{T}} \end{gathered}$ | (13) |
式中: I——单位矩阵;
P(k)——先验估计误差协方差;
R——估计误差协方差。
经过上述等式变换后, P(k)最小化的问题就转化为: 将卡尔曼增益K(k)视为自变量, 使得这个矩阵的迹最小。此时, 即可得到需要的卡尔曼增益K(k)。
| $ \begin{array}{l} \operatorname{tr}[\boldsymbol{P}(k)]=\operatorname{tr}[\overline{\boldsymbol{P}}(k)]-2 \operatorname{tr}[\boldsymbol{K}(k) \boldsymbol{C} \overline{\boldsymbol{P}}(k)]+ \\ \ \ \ \ \ \ \ \operatorname{tr}\left[\boldsymbol{K}(k)\left[\boldsymbol{C} \overline{\boldsymbol{P}}(k) \boldsymbol{C}^{\mathrm{T}}+\boldsymbol{R}\right] \boldsymbol{K}(k)^{\mathrm{T}}\right] \end{array}$ | (14) |
对K(k)求导, 并令导数等于零, 得到K(k)为
| $ \boldsymbol{K}(k)=\frac{\overline{\boldsymbol{P}}(k) \boldsymbol{C}^{\mathrm{T}}}{\boldsymbol{C} \overline{\boldsymbol{P}}(k) \boldsymbol{C}^{\mathrm{T}}+\boldsymbol{R}}$ | (15) |
至此, 得到了K(k)的表达式, 但式中还存在一个未知量P(k)。P(k)的求解过程如下。
因为
| $ \begin{gathered} \boldsymbol{U}(k)-\overline{\boldsymbol{U}}(k)[\boldsymbol{U}(k)-\overline{\boldsymbol{U}}(k)]^{\mathrm{T}}= \\ \left\{-(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}(k-1)+\boldsymbol{\delta}_{{\rm{ \mathsf{ ω} }}}(k)-\right. \\ [-(\boldsymbol{L}+\boldsymbol{G})] \hat{\boldsymbol{U}}(k-1)\} \cdot \\ \left\{-(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{U}(k-1)+\boldsymbol{\delta}_{{\rm{ \mathsf{ ω} }}}(k)-\right. \\ [-(\boldsymbol{L}+\boldsymbol{G})] \hat{\boldsymbol{U}}(k-1)\}^{\mathrm{T}} \end{gathered}$ | (16) |
所以
| $\overline{\boldsymbol{P}}(k)=-(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{P}(k-1)[-(\boldsymbol{L}+\boldsymbol{G})]^{\mathrm{T}}+\boldsymbol{Q}$ | (17) |
式中: Q——测量误差协方差。
得到P(k)的表达式后, 重新对P(k)的表达式进行整理, 得
| $ \boldsymbol{P}(k)=[\boldsymbol{I}-\boldsymbol{K}(k) \boldsymbol{C}] \overline{\boldsymbol{P}}(k)$ | (18) |
通过上述一系列的推导, 将最优估计协方差最小化问题转化为求解卡尔曼滤波增益问题, 通过对最优估计协方差求导, 得到卡尔曼滤波增益, 同时利用卡尔曼滤波增益对最优估计协方差进行化简, 从而消除FDI攻击信号的影响。
3 仿真设计
3.1 系统设计
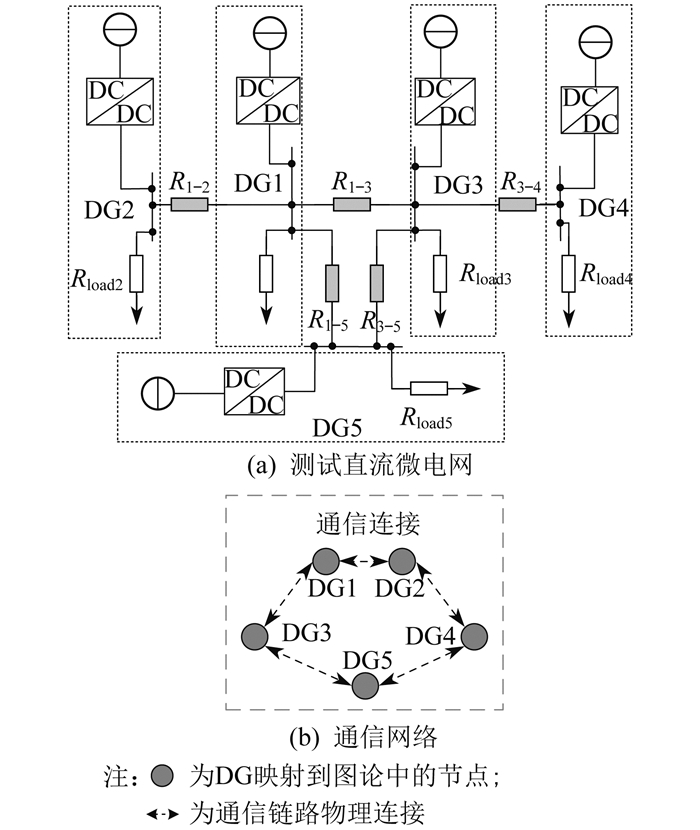
在含有5个DG(DG1—DG5)的孤岛微电网中验证本文所提出的控制策略。测试所用直流微电网及其通信网络如图 3所示。其中, Rload1~Rload5为DG内部负载; 用R1-2、R1-3、R1-5、R3-4、R3-5模拟两DG间的线路阻抗, 基准电压设为380 V。
测试直流微电网的具体参数如表 1所示。其中, Pload1~Pload5分别表示Rload1~Rload5的功率。另外, 时间步长设置为5×10-6 s, 网络邻接矩阵A和领导矩阵G分别为:
| $ \boldsymbol{A}=\left[\begin{array}{lllll} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 \end{array}\right], \boldsymbol{G}=\left[\begin{array}{lllll} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] $ |
表 1
测试直流微电网具体参数
| R1-2 | R1-3 | R3-4 | R1-5 | R3-5 |
| 0.2 Ω | 0.4 Ω | 0.4 Ω | 0.4 Ω | 0.4 Ω |
| Pload1 | Pload2 | Pload3 | Pload4 | Pload5 |
| 3 kW+2 kW | 2.5 kW | 2.5 kW+2 kW | 2.5 kW | 2.5 kW |
所有情况的模拟过程如下: 设置模拟总时间为1 s, 二次控制在t=0.1 s时开始; 在t=0.5 s时, 向Rload1增加2 kW负载; 在t=0.7 s时, 向Rload3添加2 kW负载。对两种FDI攻击案例进行研究, 包括常数FDI攻击通信链路和时变FDI攻击通信链路。
3.2 仿真案例
3.2.1 案例1
以常数FDI攻击通信链路1—2为例进行分析。假定常数攻击信号持续不断地注入到通信链路中, 攻击信号δVj=10, 利用Constant模块实现。当受到常数FDI攻击时, 各DG的电压如图 4所示。
图 4中, 当常数FDI攻击信号注入通信链路1—2时, 与通信链路1—2相连的DG1和DG2的电压明显超出其他DG的额定电压值。在t=0.1 s前, 无控制策略引入, 电压波动较大, 无法保持系统的稳定运行。t=0.1 s时, 系统引入分布式二次控制策略, 电压恢复至额定电压380 V, 但由于系统中存在攻击信号, 所以受到攻击的DG1和DG2的电压仍有较大的波动。当t=0.5 s和t=0.7 s时, DG1和DG3的负载分别增加了2 kW, 两处时间点的电压波动更大, 但在短时间内又恢复到较为恒定的电压水平, 这是由于一致性算法的影响。从整个仿真图来看, 攻击信号使得电压波动较大, 偏离额定值的情况较为严重。
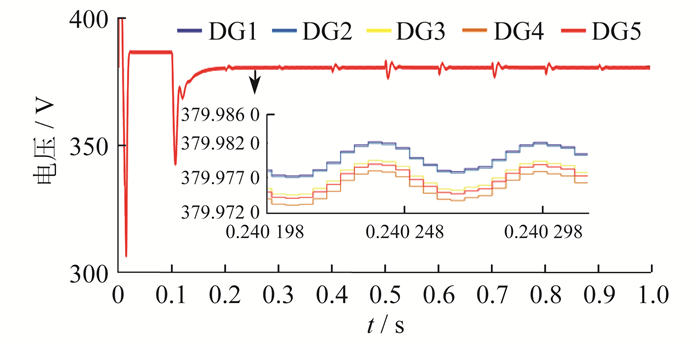
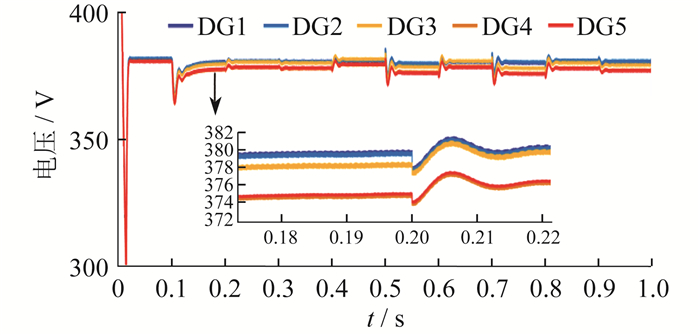
使用本文所提出的二次控制策略后, 当受到常数FDI攻击时, 各DG的电压如图 5所示。
图 5中, 在t=0.1 s时引入二次控制策略, 经过系统的调整, 在t=0.2 s时各DG的电压恢复到额定电压值380 V。当t=0.5 s和t=0.7 s时, DG1和DG3的负载分别增加2 kW, 与无抵御策略时相比, 此时的电压波动幅度更小, 并且能够迅速恢复至额定电压。因此, 本文所提出的二次控制策略可以有效抵御常数FDI攻击。
3.2.2 案例2
以时变FDI攻击通信链路1—2为例进行分析。攻击信号δVj∈[-7, 7], 利用Random模块实现。当受到时变FDI攻击时, 各DG的电压如图 6所示。
图 6中, 在t=0.1 s前, 未引入控制策略, 电压波动较大, 但由于有限区间的攻击信号符合高斯分布, 所以造成的电压波动较常数攻击信号下要小一些。当t=0.1 s时, 系统引入分布式二次控制策略, 电压调整到额定电压380 V。但由于系统中存在攻击信号, 各个DG的电压波动情况不同。这说明常数FDI攻击主要影响的是与受攻击的通信链路相连的DG, 而在时变FDI攻击下, 5个DG均受到不同程度的影响。
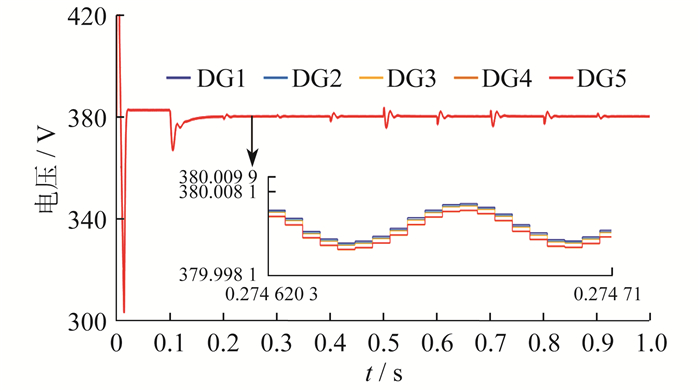
使用本文所提出的二次控制策略后, 当受到时变FDI攻击时, 各DG的电压如图 7所示。
图 7中, 在t=0.1 s时引入二次控制策略, 经过较短时间各DG的电压迅速恢复至额定电压。当t=0.5 s和t=0.7 s时, 负载突变, 此时电压的波动幅度小于无抵御策略时的电压波动幅度, 并且能够迅速恢复至额定电压值。
综上所述, 所提二次控制策略不论是应对常数FDI攻击还是时变FDI攻击, 均能够使电压迅速收敛于额定电压值, 保证攻击信号无法入侵到控制策略中, 并且所提策略在负荷变化等条件下仍然有效。
4 结语
本文提出了一种用于抵御FDI攻击的二次控制策略, 能够保障孤岛直流微电网的电压稳定性。针对通信链路中的常数及时变FDI攻击信号, 利用卡尔曼滤波算法对二次控制的输出信号进行重新估计, 能够使得各DG的电压在经受网络攻击后迅速恢复到额定电压水平。通过对含有5个DG的孤岛微电网进行仿真, 验证了所提策略的有效性。
参考文献
-
[1]王成山, 李鹏. 分布式发电、微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-14.
-
[2]沈珺, 柳伟, 李虎成, 等. 基于强化学习的多微电网分布式二次优化控制[J]. 电力系统自动化, 2020, 44(5): 198-206.
-
[3]王海峰, 李朝阳, 吕政权, 等. 泛在电力物联网环境下网络安全攻击研究[J]. 浙江电力, 2019, 38(12): 76-81.
-
[4]王明辉, 王勇, 邓乐. 光伏发电系统IEC 61850的通信安全性研究[J]. 上海电力大学学报, 2022, 38(1): 48-55.
-
[5]王成满. 基于增量式学习的网络攻击检测数学建模仿真[J]. 计算机仿真, 2021, 38(1): 273-276.
-
[6]MUSLEH A S, CHEN G, DONG Z Y. A survey on the detection algorithms for false data injection attacks in smart grids[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2218-2234. DOI:10.1109/TSG.2019.2949998
-
[7]ABHINAV S, MODARES H, LEWIS F L, et al. Synchrony in networked microgrids under attacks[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6731-6741. DOI:10.1109/TSG.2017.2721382
-
[8]王静. 网络攻击下微电网分布式经济调度方法研究[D]. 南京: 南京邮电大学, 2020.
-
[9]陈郁林, 齐冬莲, 李真鸣, 等. 虚假数据注入攻击下的微电网分布式协同控制[J]. 电力系统自动化, 2021, 45(5): 97-103.
-
[10]ZHOU Q, SHAHIDEHPOUR M, ALABDULWAHAB A, et al. A cyber-attack resilient distributed control strategy in islanded microgrids[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3690-3701.
-
[11]SAHOO S, DRAGIČEVIĆ T, BLAABJERG F. An event-driven resilient control strategy for DC microgrids[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13714-13724.
-
[12]ZUO S, BEG O A, LEWIS F L, et al. Resilient networked AC microgrids under unbounded cyber attacks[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3785-3794.
-
[13]ZUO S, ALTUN T, LEWIS F L, et al. Distributed resilient secondary control of DC microgrids against unbounded attacks[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3850-3859.
-
[14]李旭炯, 孙林花, 杨郭明. 基于逆变器的分布式光伏发电中压配电网无功优化[J]. 上海电力大学学报, 2022, 38(3): 257-263.
-
[15]马磊, 史习智. 多智能体系统中一致性卡尔曼滤波的研究进展[J]. 西南交通大学学报, 2011, 46(2): 287-293.