|
|
|
发布时间: 2023-10-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-06-30
中图法分类号: TP277;TH133.33
文献标识码: A
文章编号: 2096-8299(2023)04-0507-08
|
摘要
为了提高不同工况下的轴承故障诊断准确率, 提出了一种基于特征筛选和集成学习的轴承故障诊断方法。考虑到特征向量复杂冗余的问题, 结合特征有效性和最大均值差异提出了新的特征评分函数, 并在此基础上进一步考虑特征关联度和特征维度, 筛选出有利于变工况故障诊断的特征子集。针对单一机器学习模型故障诊断准确率不高的问题, 将AdaBoost和Stacking算法相结合构造集成学习故障诊断模型。实验结果表明: 筛选出的特征子集在相同分类器下拥有更高的故障诊断准确率; 集成学习模型相较于单一模型有更高的故障诊断准确率和鲁棒性。
关键词
轴承; 特征筛选; 集成学习; 故障诊断
Abstract
In order to improve the diagnostic accuracy of bearing failures under different operating conditions, this paper proposes a bearing fault diagnosis method based on feature selection and ensemble learning.Considering the issue of complex and redundant of feature vectors, a new feature scoring function is proposed by combining feature effectiveness and maximum mean discrepancy.Based on this, the feature correlation and feature dimensionality are further considered to select a subset of features that are beneficial for variable operating condition fault diagnosis.Considering the problem of low classification accuracy of a single machine learning model, AdaBoost and Stacking algorithm are combined to construct an ensemble learning fault diagnosis model.Experimental results demonstrate that the selected subset of features exhibits higher accuracy under the same classifier.Moreover, the ensemble learning model demonstrates higher accuracy and robustness compared to a single model.
Key words
rolling bearings; feature selection; ensemble learning; fault diagnosis
轴承长期在复杂多变的环境中高速运转, 容易发生故障[1-2], 进而造成严重的经济损失, 因此对滚动轴承进行故障诊断具有重要意义。在针对轴承的故障诊断研究中, 一般通过小波变换、经验模态分解、变分模态分解和辛几何模态分解等时频分解方法处理信号并提取特征。但随着特征维度的增加, 特征冗余、计算复杂性和诊断稳定性等问题也随之而来, 因此很多学者围绕特征优选进行了研究[3]。URBANOWICZ R J等人[4]利用Relief F算法对特征进行筛选, 但是该算法对噪声非常敏感。YANG S Y等人[5]将Fisher score与域间最大均值差异相结合, 筛选出有利于变工况故障诊断的特征。RAM V S S等人[6]提出了一种新的特征评估和筛选方法, 并对用户手臂运动识别起到很好的作用。以上方法均是对单一特征进行评估选择, 没有综合考虑特征之间的组效果。张洁等人[7]考虑到特征的有效性和互补性提出了新的特征筛选策略, 并对居民用电行为进行聚类分析, 取得了很好的效果。
随着人工智能的发展, 机器学习在轴承故障诊断中得到了广泛应用。常见的机器学习方法有支持向量机(Support Vector Machine, SVM)、K最近邻(K - Nearest Neighbor, KNN)、决策树(Decision Tree, DT)和人工神经网络等。邓平等人[8]使用SVM作为分类器, 对人体运动姿态进行识别, 然而SVM的分类性能受到模型超参数的影响[9-10]且优化单一模型的参数无法达到更好的诊断效果。为了解决这一问题, 研究人员提出了集成学习的思路。方继辉等人[11]采用XGBoost集成许多分类回归树构造集成模型, 并改进萤火虫算法对其超参数进行优化, 最终实现了对燃气轮机的故障诊断。LI H等人[12]采用了AdaBoost集成方法, 将多个决策树集成为一个模型, 实现了风机轴承的故障诊断。但AdaBoost只能集成相同的分类器, 无法集成不同质的分类器。姜万录等人[13]利用Stacking方法将多个不同质的分类器进行集成, 并用于旋转机械的故障诊断, 但Stacking集成框架受基分类器性能的影响, 因此Stacking基分类器的选择显得尤为重要。
基于上述研究, 本文利用辛几何模态分解(Symplectic Geometry Mode Decomposition, SGMD)对信号进行分解后, 提取时域、频域和时频域特征组成混合特征向量, 综合考虑区分度、冗余度、关联度和域间最大均值差异等因素提出新的特征筛选策略, 并筛选出有利于变工况故障诊断的特征。本文将Boosting和Stacking算法相结合, 提出了一个新的集成学习故障诊断模型, 从而提高故障诊断准确率。
1 特征筛选
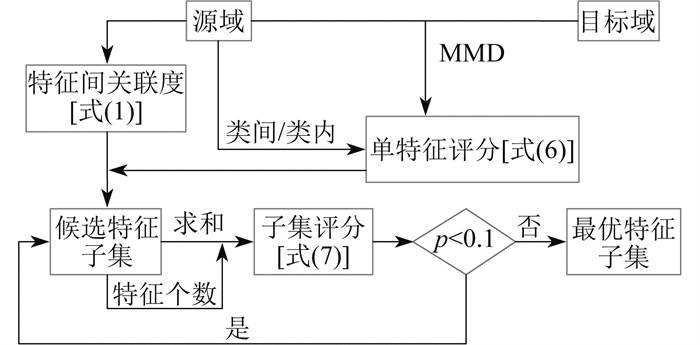
传统的特征筛选方法一般是对高维特征向量中每一个向量进行评分, 然后根据经验选出其中评分较高的前几个特征向量, 但上述方法没有考虑到特征之间的关联度, 而且最优特征的数量无法确定。本文提出了一种综合特征筛选(以下简称“综合筛选”)策略如下: 首先, 根据特征关联度对特征进行分组, 将相似的特征分为一组; 然后, 从每组特征中选出评分最高的特征组成候选特征子集; 最后, 从特征子集中不断选取最大的特征加入最优特征子集, 并进行综合评分, 直到子集综合分数低于阈值后完成筛选。
1.1 特征关联度
利用皮尔逊相关系数[14]作为关联度指数, 将具有高关联度的特征进行分组, 并根据评分进行特征的初步筛选。特征x和特征y的关联度指数计算公式为
| $ \rho_{x y}=\frac{\operatorname{cov}(x, y)}{\sigma_x \sigma_y} $ | (1) |
式中: ρxy——特征x和特征y的关联度指数, 范围为[-1, 1], ρxy越趋近于1则表示x与y越相关;
cov(x, y)——特征x和特征y的协方差;
σx、σy——特征x和特征y标准差。
1.2 单一特征评分函数构造
由于不同特征向量的分类准确率和跨域故障诊断准确率会有所不同, 因此需要对特征向量进行筛选。本文从特征有效性和适合迁移两方面构造单一特征评分函数。
为了体现不同特征对分类的有效性, 需要对每个特征都进行评价。将区分度指标定义为完全区分的样本个数占全部样本个数的比重。不同特征的区分度如图 1所示。
对于k分类的特征可以构造出k×k的区分度矩阵D为
| $ \boldsymbol{D}=\left[\begin{array}{ccc} d_{11} & \cdots & d_{1 k} \\ \vdots & & \vdots \\ d_{k 1} & \cdots & d_{k k} \end{array}\right] $ | (2) |
| $ d_{i j}=1-\frac{n_{i j}}{n_i+n_j} $ | (3) |
式中: dij——同一特征下第i类和第j类的区分度;
nij——两类不能区分的特征数量;
ni、nj——第i类和第j类的特征数量。
对于同类区分度的计算, 结果越聚合则说明区分度越低。引入平均距离计算同类特征聚合程度Sj为
| $ S_j=\frac{1}{n} \sum\limits_{i=1}^n\left(x_{j i}-\overline{x_j}\right)^2 $ | (4) |
式中: n——样本总数;
xji——第j类的第i个样本;
xj——第j类样本均值。
引入最大均值差异(Maximum Mean Discrepancy, MMD)[15]来衡量特征的可迁移性。MMD常用于衡量不同工况之间特征的分布差异。其值越大则说明不同工况的分布差异越大, 不适合特征迁移; 反之, 则更适合迁移。MMD的公式为
| $ M\left(X_{\mathrm{s}}, X_{\mathrm{t}}\right)=\left\|\frac{1}{n_{\mathrm{s}}} \sum\limits_{i=1}^{n_{\mathrm{s}}} \varphi\left(X_{\mathrm{s}, i}\right)-\frac{1}{n_{\mathrm{t}}} \sum\limits_{j=1}^{n_t} \varphi\left(X_{\mathrm{t}, j}\right)\right\|^2 $ | (5) |
式中: M——最大均值差异;
Xs、Xt——源域和目标域;
ns、nt——源域和目标域的样本数量;
φ——再生核Hilbert空间中的非线性映射函数。
综上, 一个特征的类间区分度越大、类内区分度越低以及不同域差异越小, 则该特征的评分就越高。
定义k分类特征的评价函数F为
| $ F = \frac{{\frac{{s({\boldsymbol{D}})}}{2}}}{{M\sum\limits_k {{S_j}} }} $ | (6) |
式中: s(D)——矩阵D所有元素的和。
1.3 特征子集综合评分
2 基于集成学习的故障诊断模型
2.1 AdaBoost集成方法
AdaBoost是一种基于Boosting集成算法改进的集成学习方法, 通过将相同的弱分类器不断迭代集成一个强分类器。在第1次迭代中, 基于相同权重D0的训练集训练一个弱分类器hi, 并根据其分类器效果获取弱分类器的权重αi; 然后, 根据αi更新下一次训练集的权重Di+1; 最后, 将所有弱分类器的结果加权, 得到最终的分类结果。
| $ \alpha_i=\frac{1}{2} \ln \frac{1-\varepsilon_i}{\varepsilon_i} $ | (8) |
式中: εi——误差。
样本权重Di的更新公式为
| $ D_{i+1}=\frac{D_i}{\eta_i} \mathrm{e}^{-\alpha_i y_i h_i} $ | (9) |
式中: ηi——归一化因子;
yi——实际标签结果;
hi——分类器输出结果。
通过加权得到强分类器H, 公式为
| $ H=\sum\limits_{i=1}^n \alpha_i h_i $ | (10) |
2.2 Stacking集成方法
Stacking通过结合多个不同基础模型的预测结果来训练元模型, 再利用元模型来得到更准确的预测结果。
Stacking集成模型一般分为两层。第1层利用不同的基分类器预测同一数据集的分类结果, 然后将预测结果作为第2层的输入, 并继续训练, 进而得到最终结果, 以达到提高模型泛化能力和分类准确率的目的。但Stacking的分类结果容易出现过拟合, 因此需要对第1层的基分类器进行交叉验证。
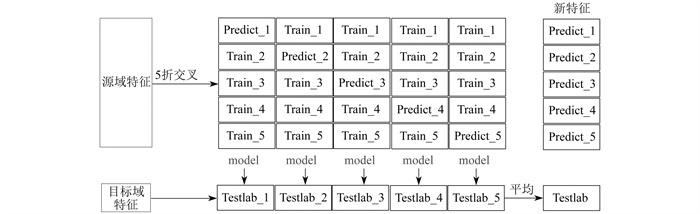
Stacking基分类器的5折交叉训练过程如图 3所示。其中, model表示分类模型, 将训练集分为5折其中4折用于训练模型, 1折用于预测, 重复5次; Train表示训练集; Predict表示预测的结果; Testlab表示在训练好的模型下目标域的预测结果。
2.3 集成学习故障诊断模型
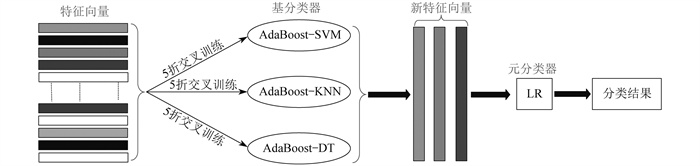
AdaBoost将多个相同的弱分类器集成为一个强分类器, 具有准确率高且不容易过拟合的优点, 但该方法只能集成相同的分类器; Stacking则能够集成不同类型的分类器, 充分发挥各种分类器的优点, 但其分类准确率过于依赖基分类器的分类准确性。基于此, 本文将AdaBoost和Stacking相结合来构成集成模型。首先, 用AdaBoost将SVM、KNN和DT进行集成, 构成3个Stacking的基分类器。然后, 利用逻辑回归作为元分类器构成最终的集成学习故障诊断模型(以下简称“集成模型”)。集成模型如图 4所示。
3 实验与分析
3.1 实验数据说明
本文选用西储大学滚动轴承数据, 轴承型号为6205 - 2RSJEM SKF型深沟球轴承, 采集1 730 r/min、1 750 r/min和1 772 r/min转速下的3个数据集, 并分别记为A、B、C。其中, 每个数据集采样频率均为12 kHz, 包含内圈故障、外圈故障和滚动体故障3种故障类型。每种故障类型又分别包含3种不同单点损伤直径(0.177 8 mm、0.355 6 mm、0.533 4 mm)故障。与正常状态合计共10种类别, 每种类别200个样本, 共2 000个样本。
3.2 特征筛选
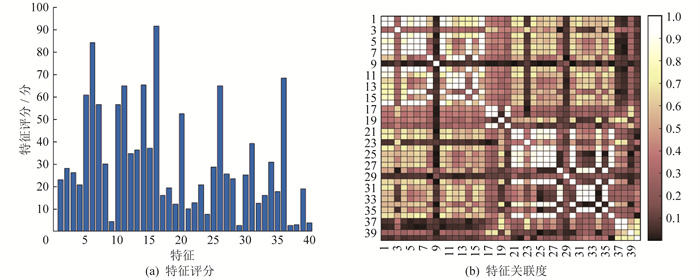
对源域和目标域2个域的信号采用辛几何模态分解[17], 并计算前2个辛几何分量的最大值、最小值、平均值、峰峰值、绝对平均值、方差、标准差、峭度、偏度、均方根、波形因子、峰值因子、脉冲因子、绝对均方根、裕度、频率均值、重心频率、频率均方根、频率标准差和排列熵作为特征向量。然后, 按顺序将40个特征进行编号和评分, 并进行关联度分析, 结果如图 5所示。
将关联度大于0.9的特征组合在一起, 并从每组中选出评分最高的特征。初步筛选结果如表 1所示。
表 1
初步筛选结果
| 分组 | 特征序号 | 筛选 | 分组 | 特征序号 | 筛选 | |
| 1 | 1, 2, 4, 5, 7, 10, 14 | 14 | 10 | 21, 22, 24, 25, 26, 27, 30, 34, 36 | 36 | |
| 2 | 3 | 3 | 11 | 23 | 23 | |
| 3 | 6, 16 | 16 | 12 | 28 | 28 | |
| 4 | 8, 12, 13, 15 | 12 | 13 | 29 | 29 | |
| 5 | 9 | 9 | 14 | 31 | 31 | |
| 6 | 11 | 11 | 15 | 32, 33, 35 | 35 | |
| 7 | 17, 18 | 18 | 16 | 37, 38 | 38 | |
| 8 | 19 | 19 | 17 | 39 | 39 | |
| 9 | 20 | 20 | 18 | 40 | 40 |
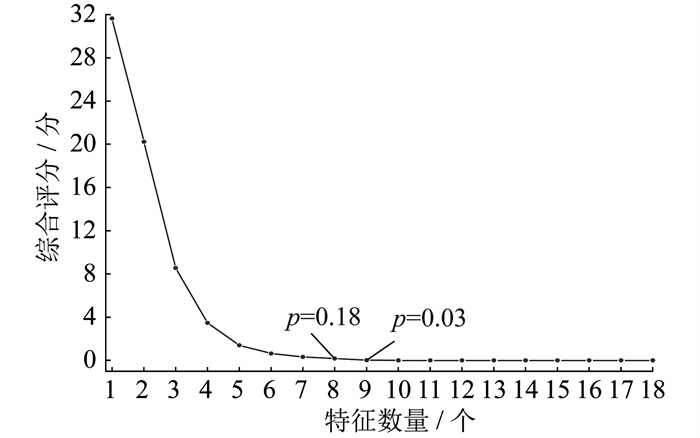
通过初步的筛选, 从40个特征中筛选出18个特征作为候选特征。将候选特征逐一加入到最优特征子集中, 得到不同数量下特征子集的综合评分, 并根据评分筛选出3、11、12、14、16、20、31、36组成最优特征子集。不同数量下特征子集的综合评分如图 6所示。
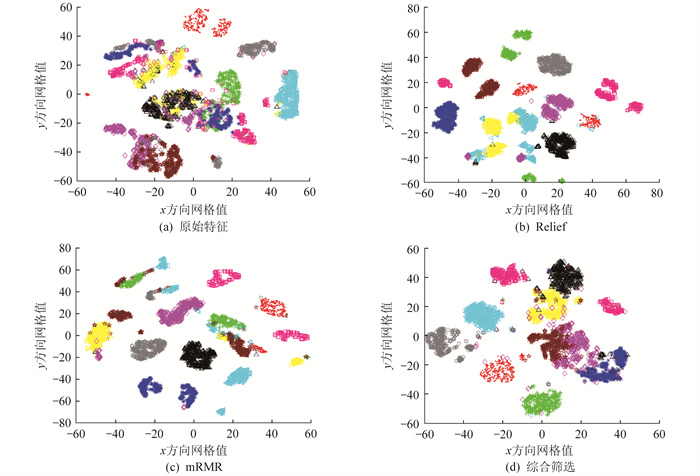
为验证本文所提策略的有效性, 选用传统的特征筛选方法Relief和mRMR与本文所提出的综合筛选方法进行对比。采用t分布随机邻居嵌入(t - SNE)降维方法, 将原始特征与各种方法筛选的结果以二维散点图的形式呈现, 结果如图 7所示。
由图 7可以看出, 原始特征不仅在不同类别间不易区分, 而且不同域之间的分布也存在一定的差异。传统的特征筛选方法Relief和mRMR能将不同类别区分开, 但在不同域之间差异依旧存在。本文所提出的综合筛选方法所筛选出的特征, 不仅使不同类别间较易区分, 而且相同类别在不同域的差异也有所降低。这证明本文的筛选策略更有利于变工况故障诊断。
3.3 基于集成学习的变工况故障诊断
在完成特征筛选之后, 综合筛选的特征仍会存在一些类别较易混淆, 因此利用集成学习模型进行故障诊断。
为了验证集成学习模型的实用性, 本文共设置6个迁移任务, 分别为A→B、A→C、B→A、B→C、C→A、C→B。
对6个迁移任务分别采用SVM、KNN、DT与集成模型进行故障诊断实验。故障诊断准确率如表 2所示。
表 2
不同模型下6个迁移任务的故障诊断准确率
| 模型 | A→B | A→C | B→A | B→C | C→A | C→B | 平均 |
| SVM | 97.30 | 91.65 | 91.10 | 91.10 | 83.25 | 99.50 | 93.15 |
| KNN | 96.55 | 92.65 | 89.80 | 95.70 | 86.80 | 99.00 | 93.42 |
| DT | 94.80 | 80.30 | 85.20 | 91.20 | 89.00 | 97.30 | 89.63 |
| 集成模型 | 99.55 | 96.75 | 96.65 | 98.25 | 90.00 | 100.00 | 96.87 |
由表 2的故障诊断结果可以看出, 6个迁移任务中集成模型的准确率均高于单一模型。集成模型的平均准确率相较于单一模型分别提高了3.72%、3.45%、7.24%。这说明集成模型能够进一步提高故障诊断的准确性。
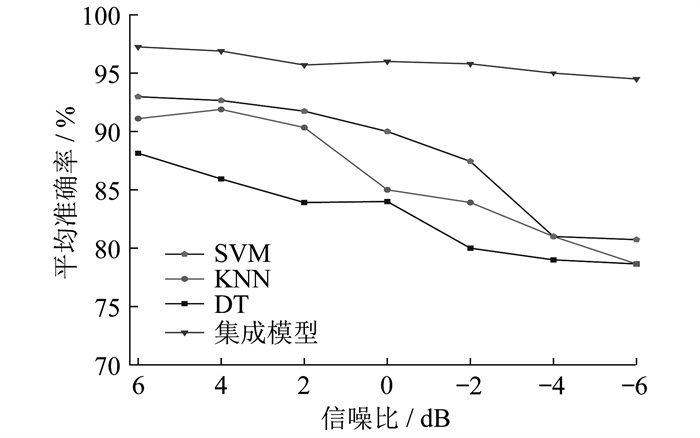
现实中采集到的轴承信号往往存在大量噪声, 为了进一步验证集成模型的性能, 在原始的振动信号中加入不同信噪比的高斯白噪声模拟现实故障信号。对添加噪声的信号进行辛几何模态分解并提取特征, 通过综合特征筛选后, 采用SVM、KNN、DT和集成模型进行故障诊断。不同信噪比下各模型故障诊断平均准确率如图 8所示。
根据表 2和图 8的结果可知, 加入噪声后所有模型的故障诊断准确率都有所下降。随着噪声信噪比的降低, 单一模型的准确率快速下降, 但本文所提出的集成模型则较为稳定, 准确率保持在94%~98%之间。这说明集成模型不仅有较高的故障诊断准确率, 而且还有一定的鲁棒性。
4 结语
本文针对变工况条件下风机轴承故障诊断准确率低的问题, 提出了一种基于特征筛选和集成学习的轴承故障诊断方法。通过实验证明, 本文提出的特征筛选策略所筛选出的特征相较于传统方法更有利于变工况分类; 在相同的特征集下, 集成学习模型相较于单一模型有较高的故障诊断准确率, 且在不同噪声下表现也更为稳定。
参考文献
-
[1]ZHANG X, ZHAO B Y, LIN Y. Machine learning based bearing fault diagnosis using the case western reserve university data: a review[J]. IEEE Access, 2021, 9: 155598-155608. DOI:10.1109/ACCESS.2021.3128669
-
[2]潘成龙, 应雨龙. 基于二维卷积神经网络的滚动轴承变工况故障诊断方法[J]. 上海电力大学学报, 2022, 38(1): 29-34.
-
[3]牛勇, 李华鹏, 刘阳惠, 等. 超高维数据特征筛选方法综述[J]. 应用概率统计, 2021, 37(1): 69-110.
-
[4]URBANOWICZ R J, MEEKER M, LA CAVA W, et al. Relief-based feature selection: introduction and review[J]. Journal of Biomedical Informatics, 2018, 85: 189-203. DOI:10.1016/j.jbi.2018.07.014
-
[5]YANG S Y, ZHENG X X. A novel bearing fault diagnosis method with feature selection and manifold embedded domain adaptation[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(14): 8185-8197. DOI:10.1177/09544062221083573
-
[6]RAM V S S, KAYASTHA N, SHA K W. OFES: optimal feature evaluation and selection for multi-class classification[J]. Data & Knowledge Engineering, 2022, 139: 102007.
-
[7]张洁, 夏飞, 袁博, 等. 基于特征优选策略的居民用电行为聚类方法[J]. 电力系统自动化, 2022, 46(6): 153-159.
-
[8]邓平, 吴明辉. 基于机器学习的人体运动姿态识别方法[J]. 中国惯性技术学报, 2022, 30(1): 37-43.
-
[9]周晓华, 冯雨辰, 陈磊, 等. 改进秃鹰搜索算法优化SVM的变压器故障诊断研究[J]. 电力系统保护与控制, 2023, 51(8): 118-126.
-
[10]HUANG Q H, WANG C, YE Y, et al. Recognition of EEG based on improved black widow algorithm optimized SVM[J]. Biomedical Signal Processing and Control, 2023, 81: 104454.
-
[11]方继辉, 李阳. 基于IFA-XGBoost的燃气轮机故障诊断[J]. 上海电力大学学报, 2021, 37(4): 367-372.
-
[12]LI H, LI F, JIA R, et al. Research on the fault feature extraction of rolling bearings based on SGMD-CS and the AdaBoost framework[J]. Energies, 2021, 14(6): 1555.
-
[13]姜万录, 赵岩, 李振宝, 等. 多模型Stacking集成学习的旋转机械故障诊断方法[J]. 液压与气动, 2023, 47(4): 46-58.
-
[14]LI Z X, YANG Y, LI L W, et al. A weighted Pearson correlation coefficient based multi-fault comprehensive diagnosis for battery circuits[J]. Journal of Energy Storage, 2023, 60: 106584.
-
[15]王琦, 邓林峰, 赵荣珍. 基于一维CNN迁移学习的滚动轴承故障诊断[J]. 振动、测试与诊断, 2023, 43(1): 24-30.
-
[16]周侯伯, 肖桂荣, 林炫歆, 等. 基于特征筛选与差分进化算法优化的滑坡危险性评估方法[J]. 地球信息科学学报, 2022, 24(12): 2373-2388.
-
[17]PAN H Y, YANG Y, LI X, et al. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis[J]. Mechanical Systems and Signal Processing, 2019, 114: 189-211.