|
|
|
发布时间: 2023-10-28 |
其他研究 |
|
|
|
收稿日期: 2023-04-29
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2023)05-0500-07
|
摘要
基于多智能体的一致性原理, 提出了一种微电网经济与环境综合最优的分布式调度方法。该调度方法不再借助于领导跟随的一致性算法模式, 而是基于机器人系统的工作模式, 各节点通过存储最新的功率缺额, 得到局部功率缺额, 并用其替代全局功率缺额, 解决了分布式多目标经济调度获取全局信息困难的问题。同时, 该算法能够适应微电网系统负荷变动的特性, 可实现多种情景下的微电网综合最优调度。算例仿真结果验证了所提方法的有效性。
关键词
微电网; 多目标经济调度; 一致性算法
Abstract
Based on consensus algorithms, a distributed multi-objective economic dispatch algorithm on environmental protection and economy is proposed for a micro-grid.Through estimating the global power mismatch by local power mismatch based on multi-robot task systems, this method doesn't resort to the leader-follower consensus algorithm any more, which can avoid the occurrence of the difficulties in getting the global information for consensus algorithm.According to multi-robot task systems, each node on the communication graph saves the most up-to-date information from the other nodes.Moreover, it is shown that the proposed method can adapt to the varying load demand of the micro-grids and achieve a variety of multi-objective economic dispatch situations in the micro-grid.Simulation case verifies the validity of our results.
Key words
micro-grid; multi-objective dispatch; consensus algorithms
经济调度是电力系统中的基本问题之一。它是将所需的发电量分配给多个发电机组, 在满足发电机出力等约束条件下实现供需平衡[1-2]。经济调度算法主要有集中式和分布式两类。传统电力系统经济调度问题主要采用集中式经济调度算法求解[1], 调度中心要承受巨大的计算负担和通信压力, 且可靠性和鲁棒性不高; 而分布式经济调度算法克服了集中式的不足, 越来越受到业内关注。分布式算法强调参与调度的各发电单元的自主决策和个体智能, 通过各单元的协同配合实现经济调度目标。文献[3]基于多智能体的一致性原理, 将微增成本视为一致性变量, 提出了领导跟随模式的分布式经济调度策略。该模式受到了广泛关注和应用, 现在仍有很多工作延续使用[4-10]。但其依赖于领导者能够获取功率差额这一假设, 对网络连接的要求较高, 适应性较差。
学者们针对全局功率缺额获取困难展开了研究, 如文献[11]提出了一种无领导的分布式经济调度算法, 将发电-负荷功率平衡约束分解至各发电单元的个体经济调度优化模型中, 但该算法对发电单元的初值有要求, 难以适应系统负荷的变化; 文献[12]为了获取全局信息, 提出了利用局部负荷信息估计全局负荷的算法, 但该算法需在母线之外配备新的通信线路, 不易实现。文献[13]提出了一种基于一致性原理和梯度下降法的完全分布式优化调度策略。
值得指出的是, 文献[14]提出了一种自组织的分布式经济调度方案, 仍将微增成本视为一致性变量, 但不再引入领导者角色。该方案利用机器人系统的工作模式, 在每个节点只保留通过网路传输得到的其余节点的最新功率缺额信息, 进而整合得到该节点处的局部功率缺额。同时, 该算法不需要设置发电单元的出力初值之和与负荷相等, 可以灵活应对系统负荷变动的情况。文献[13-14]仅考虑了发电成本最小单目标问题, 并没有考虑微电网参与节能减排的问题。由于节能减排是当今能源发展中的重要问题, 因此在设计分布式经济调度方案时有必要考虑如何减小环境污染[15-20]。
本文将研究微电网多目标经济调度, 不但考虑经济最优, 同时考虑减少污染气体排放量。首先, 综合考虑传统发电机发电成本、污染气体排放及储能成本, 构建微电网多目标优化模型; 其次, 通过线性加权将多目标优化问题转化为单目标优化问题; 再次, 利用多智能体的一致性原理设计一种分布式经济调度方案; 最后, 基于IEEE14节点系统, 通过数值仿真验证方案的有效性。其中, 为了获得局部功率缺额, 本文采用了文献[14]中的机器人系统工作模式, 从而解决了全局信息获取困难的问题。
1 微电网多目标调度模型
本文同时考虑经济和环境两个方面, 通过优化发电机、储能单元等可控电力元件的有功功率, 使得电网的运行成本和污染气体排放综合目标最小化。
1.1 经济成本的优化目标
经济成本的优化目标是使全系统总发电成本最小。本文中微电网包含发电单元、储能单元、负荷单元3种, 分别用集合SG、SB、SD表示。发电单元和储能单元的成本函数可近似用二元函数表示为[15]
| $ F_{\mathrm{G} i}\left(P_{\mathrm{G} i}\right)=a_i P_{\mathrm{G} i}^2+b_i P_{\mathrm{G} i}+c_i, i \in S_{\mathrm{G}} $ | (1) |
| $ F_{\mathrm{B} j}\left(P_{\mathrm{B} j}\right)=\tilde{a_j} P_{\mathrm{B} j}^2, j \in S_{\mathrm{B}} $ | (2) |
式中: FGi(PGi)——第i个发电单元的成本函数;
PGi——第i个发电单元的输出功率;
ai、bi、ci——第i个发电单元的成本参数;
FBj(PBj)——第j个储能单元的成本函数;
PBj——第j个储能单元的输出功率, 其值为正时放电, 值为负时充电;
等式约束条件为
| $ \sum\limits_{i \in S_{\mathrm{G}}} P_{\mathrm{G} i}+\sum\limits_{j \in S_{\mathrm{B}}} P_{\mathrm{B} j}=P_{\mathrm{D}}+P_{\mathrm{LOSS}} $ | (3) |
式中: PD——电网总负荷;
PLOSS——电网网损。
不等式约束条件为
| $ P_{\mathrm{G} i}^{\min } \leqslant P_{\mathrm{G} i} \leqslant P_{\mathrm{G} i}^{\max }, \quad P_{\mathrm{B} j}^{\min } \leqslant P_{\mathrm{B} j} \leqslant P_{\mathrm{B} j}^{\max } $ | (4) |
式中: PGimin、PGimax——第i个发电单元输出功率的下限和上限;
PBjmin、PBjmax——第j个储能单元输出功率的下限和上限。
1.2 环境成本的优化目标
环境成本的优化目标是使系统中传统燃料发电机的污染气体排放量最小。目标函数为
| $ \min \sum\limits_{i \in S_{\mathrm{G}}} E_i\left(P_{\mathrm{G} i}\right)=\sum\limits_{i \in S_{\mathrm{G}}} \alpha_i P_{\mathrm{G} i}^2+\beta_i P_{\mathrm{G} i}+\gamma_i $ | (5) |
式中: Ei(PGi)——第i个发电单元的污染气体排放量, 可以按一定规则换算成费用[18];
αi、βi、γi——第i个发电单元的污染气体排放系数。
1.3 多目标模型
使用线性加权法将多目标问题转化为单目标问题, 同时满足式(3)和式(4), 具体可表示为
| $ \begin{gathered} \min w_1\left[\sum\limits_{i \in S_{\mathrm{G}}} F_{\mathrm{G} i}\left(P_{\mathrm{G} i}\right)+\sum\limits_{j \in S_{\mathrm{B}}} F_{\mathrm{B} j}\left(P_{\mathrm{B} j}\right)\right]+ \\ w_2 \sum\limits_{i \in S_{\mathrm{G}}} E_i\left(P_{\mathrm{G} i}\right) \end{gathered} $ | (6) |
式中: w1>0, w2>0, 且w1+w2=1。
利用拉格朗日等式将式(6)转化成无约束问题, 具体为
| $ \begin{gathered} w_1\left[\sum\limits_{i \in S_{\mathrm{G}}} F_{\mathrm{G} i}\left(P_{\mathrm{G} i}\right)+\sum\limits_{j \in S_{\mathrm{B}}} F_{\mathrm{B} j}\left(P_{\mathrm{B} j}\right)\right]+ \\ w_2 \sum\limits_{i \in S_{\mathrm{G}}} E_i\left(P_{\mathrm{G} i}\right)+\lambda \Delta P \end{gathered} $ | (7) |
| $ \Delta P=P_{\mathrm{D}}+P_{\mathrm{LOSS}}-\sum\limits_{i \in S_{\mathrm{G}}} P_{\mathrm{G} i}-\sum\limits_{j \in S_{\mathrm{B}}} P_{\mathrm{B} j} $ | (8) |
式中: λ——拉格朗日乘子;
ΔP——系统功率缺额。
对式(7)中的λ、PGi、PBj分别求偏导, 并求解其方程, 可得
| $ \left\{\begin{array}{l} w_1\left(2 a_i P_{\mathrm{G} i}+b_i\right)+w_2\left(2 \alpha_i P_{\mathrm{G} i}+\beta_i\right)-\lambda=0 \\ w_1\left(2 \tilde{a_j} P_{\mathrm{B} j}\right)-\lambda=0 \end{array}\right. $ | (9) |
对应发电单元和储能单元的拉格朗日乘子λGi和λBj分别为
| $ \left\{\begin{array}{l} \lambda_{\mathrm{G} i}=2 \hat{a}_i P_{\mathrm{G} i}+\hat{b}_i \\ \lambda_{\mathrm{B} j}=w_1\left(2 \tilde{a_j} P_{\mathrm{B} j}\right) \end{array}\right. $ | (10) |
其中,
| $ \hat{a}_i=w_1 a_i+w_2 \alpha_i, \quad \hat{b}_i=w_1 b_i+w_2 \beta_i $ | (11) |
由式(3)可得最优解λ*为
| $ {\lambda ^*} = \frac{{{P_{\text{D}}} + {P_{{\text{Loss}}}} + \sum\limits_i {\frac{{{{\hat b}_i}}}{{2{{\hat a}_i}}}} }}{{\sum\limits_i {\frac{1}{{2{{\hat a}_i}}}} + \frac{1}{{{w_1}}}\sum\limits_j {\frac{1}{{2\widetilde {{a_j}}}}} }} $ | (12) |
2 微电网经济调度方法设计
采用图G=(V, E, A)表示电力元件以及电力元件间通信交互的路径, 其中V表示图G的顶点(即电网中各节点), E表示图G的边集, A表示加权的非负链接矩阵。A中的元素aij是顶点i和j之间边的权重。用Ni代表顶点i的邻居, 约定顶点i与其自身相连。同理可得ais、ajs、ats, 以及Nj、Nt的含义。
给微电网中每个节点配备一个智能体, 并相应地配置发电单元、储能单元和负荷单元的微增成本变量λi(k)、λj(k)、λt(k)(k为迭代次数, k=0, 1, 2, …), 其更新方式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _i}(k + 1) = \sum\limits_{s \in {N_i}} {{a_{is}}} {\lambda _s}(k) + {\varepsilon _i}(k)\Delta {P_{{\text{G}}i}}(k), \forall i \in {S_{\text{G}}}} \\ {{\lambda _j}(k + 1) = \sum\limits_{s \in {N_j}} {{a_{js}}} {\lambda _s}(k) + \widetilde {{\varepsilon _j}}(k)\Delta {P_{{\text{B}}j}}(k), \forall j \in {S_{\text{B}}}} \\ {{\lambda _t}(k + 1) = \sum\limits_{s \in {N_t}} {{a_{ts}}} {\lambda _s}(k), \quad \forall t \in {S_{\text{D}}}} \end{array}} \right. $ | (13) |
式中:
ΔPGi(k)——第i个发电单元处的局部功率缺额;
ΔPBj(k)——第j个储能单元处的局部功率缺额。
由式(13)可知, 纯负荷节点的微增成本变量的更新规则与其他节点不同。
2.1 初值选择
按照各发电单元的出力约束条件式(4)选取合适的初值PGi(0)和PBj(0), 不妨取为出力约束的下限。其中, PGi(0)和PBj(0)的选取没有利用全局系统总负荷, 故算法是完全分布式的。再根据式(13)计算出相应的发电单元和储能单元的微增成本变量λi(0)和λj(0)。约定纯负荷节点的微增成本变量λt(0)为零。
发电单元和储能单元的功率更新公式为
| $ {P_{{\text{G}}i}}(k) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} P_{{\text{G}}i}^{\min }, \quad {\lambda _i}(k)2{{\hat a}_i}P_{{\text{G}}i}^{\min } + {{\hat b}_i} \hfill \\ \frac{{{\lambda _i}(k) - {{\hat b}_i}}}{{2{{\hat a}_i}}}, \quad 2{{\hat a}_i}P_{{\text{G}}i}^{\min } + {{\hat b}_i} \hfill \\ \end{gathered} \\ {{\lambda _i}(k)2{{\hat a}_i}P_{{\text{G}}i}^{\max } + {{\hat b}_i}} \\ {P_{{\text{G}}i}^{\max }, \quad {\lambda _i}(k)2{{\hat a}_i}P_{{\text{G}}i}^{\max } + {{\hat b}_i}} \end{array}} \right. $ | (14) |
| $ P_{\mathrm{B} j}(k)=\left\{\begin{array}{c} P_{\mathrm{B} j}^{\min }, \quad \lambda_j(k) \leqslant 2 w_1 \tilde{a_j} P_{\mathrm{B} j}^{\min } \\ \frac{\lambda_j(k)}{2 w_1 \tilde{a_j}}, \quad 2 w_1 \tilde{a_i} P_{\mathrm{B} j}^{\min } \leqslant \\ \lambda_j(k) \leqslant 2 w_1 \tilde{a_j} P_{\mathrm{B} j}^{\max } \\ P_{\mathrm{B} j}^{\max }, \quad \lambda_j(k) \geqslant 2 w_1 \tilde{a_j} P_{\mathrm{B} j}^{\max } \end{array}\right. $ | (15) |
2.2 局部功率缺额的获取
定义微电网各个节点处的局部功率负荷变量为
| $ \Delta p_i(k)= \begin{cases}p_{\mathrm{D} i}-P_{\mathrm{G} i}(k), & i \in S_{\mathrm{G}} \\ p_{\mathrm{D} i}-P_{\mathrm{B} i}(k), & i \in S_{\mathrm{B}} \\ p_{\mathrm{D} i}, & i \in S_{\mathrm{D}}\end{cases} $ | (16) |
| $ \sum\limits_i \Delta p_i(k)=P_{\mathrm{D}}-\sum\limits_{i \in S_{\mathrm{G}}} P_{\mathrm{G} i}-\sum\limits_{j \in S_{\mathrm{B}}} P_{\mathrm{B} j} $ | (17) |
式中: Δpi(k)——第i个节点处的局部功率负荷变量;
pDi——母线i上的负荷需求。
利用机器人系统的工作模式来获取局部功率缺额。为了叙述简单, 将不再区分ΔPGi(k)或ΔPBj(k), 统一用ΔPi(k)表示。记xi为节点i处的向量, si为其时间标签, xij和sij为xi和si的第j个分量, 并约定xii为节点i处局部功率缺额, xij表示节点i处通过网络获得的第j个节点最新的功率缺额(i≠j), xij通过时间标签的分量sij从邻居母线获得。具体公式为[14]
| $ \left\{ {\begin{array}{*{20}{l}} {{s_{ii}}(k + 1) = k + 1} \\ {{x_{ii}}(k + 1) = \Delta {p_i}(k)} \\ {{s_{ij}}(k + 1) = \mathop {\max }\limits_{h \in {N_i}} {s_{hj}}(k)} \\ {{x_{ij}}(k + 1) = {x_{i_j^*j}}(k + 1)} \\ {i_j^* = \mathop {\operatorname{argmax} }\limits_{h \in {N_i}} {s_{hj}}(k)} \end{array}} \right. $ | (18) |
由式(18)可知, 向量xi(k)存储的是母线i与其他母线j的信息交互中所获得的功率缺额。因此, 母线i处的局部功率缺额可定义为
| $ \Delta P_i(k)=\sum\limits_{j \in N_i} x_{i j}(k) $ | (19) |
为了简化问题, 本文不考虑电网的网损。本文提出的分布式算法步骤如下。
步骤1确定各节点的初始功率, 并利用式(13)得到发电单元和储能单元的微增成本变量λi(0)和λj(0), 约定λt(0)=0。
步骤2按照式(16)~式(19)计算各节点处的局部功率缺额ΔPi(k)。
步骤3按照式(13)更新各节点的微增成本变量λi(k+1)、λj(k+1)、λt(k+1)。
步骤4根据上述更新后的λi(k+1)、λj(k+1)、λt(k+1), 按照式(14)、式(15)更新PGi(k+1)和PBj(k+1)。
步骤5按照式(16)~式(19)计算各节点处的局部功率缺额ΔPi(k+1);然后判断ΔPi(k+1) ≤δ(δ为功率偏差允许最大值, 一般取较小的数)是否成立。若成立, 则算法结束; 否则, 跳转至步骤3, 继续进行迭代和功率调整。
3 算例分析
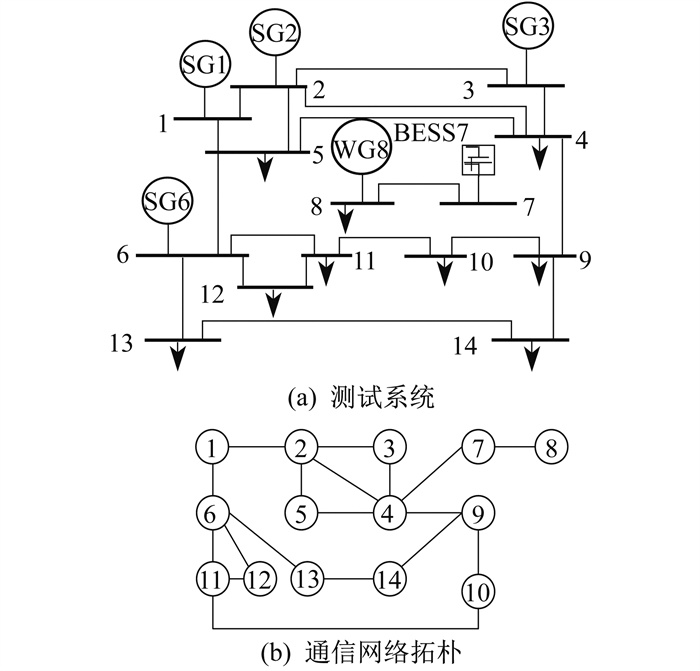
IEEE14节点的测试系统及其通信网络拓扑如图 1所示。在节点1、2、3、6处分别接入发电单元(记为SG1, SG2, SG3, SG6), 节点7接入由BESS构成的储能单元, 节点8接入1个风力发电机(记为WG8)。
3.1 参数介绍
发电单元的成本参数[19]、发电约束和污染气体排放系数[19]如表 1所示。储能单元成本系数取自文献[12]。
表 1
发电单元的成本参数、发电约束和污染气体排放系数
| 发电单元 | a/(t·MWh-1) | b/(t·MWh-1) | c/(t·h-1) | PGimax/MW | PGimin/MW | αi/(t·MWh-1) | βi/(t·MWh-1) | γi/(t·h-1) |
| SG1 | 0.000 450 | 0.24 | 7.51 | 180 | 50 | 0.001 125 | 0.600 | 18.77 |
| SG2 | 0.000 287 | 0.145 | 5.27 | 450 | 150 | 0.000 574 | 0.290 | 10.24 |
| SG3 | 0.000 337 | 0.181 | 5.53 | 240 | 80 | 0.000 674 | 0.362 | 11.06 |
| SG6 | 0.000 315 | 0.168 | 5.25 | 400 | 100 | 0.000 630 | 0.404 | 13.08 |
| WG8 | 60 | 0 |
该微电网系统正常运行时, 各节点负荷需求pDi如表 2所示。
表 2
各节点的负荷需求
| 节点 | pDi | 节点 | pDi | 节点 | pDi | ||
| 1 | 0 | 6 | 111.2 | 11 | 3.5 | ||
| 2 | 21.7 | 7 | 0 | 12 | 126.1 | ||
| 3 | 66.2 | 8 | 100.0 | 13 | 13.5 | ||
| 4 | 97.8 | 9 | 29.5 | 14 | 263.9 | ||
| 5 | 7.6 | 10 | 9.0 |
由表 2中参数可计算出, 此时系统的总负荷为PD=850 MW。风力发电机的出力为10 MW。根据近期煤炭行业行情, 煤炭单价取145 $/t, 将表 1中的煤耗特性系数乘以此单价, 可得到发电单元成本函数式(1)中的成本参数。依据各地《排污费征收标准管理办法》中的规定, 废气排污费暂且取为294 $/t, 将表 1中的污染气体排放特性系数乘以此数, 可将污染气体排放量转化为费用。取多目标函数式(6)中的参数w1=0.5。依据文献[14]中的说明, 式(13)中的调整系数可取为εi(k)=ai/ni(k), 其中ni(k)表示节点i在k次迭代后接受到的所有节点的个数。例如, 对于图 1中的节点1, n1(1)=1, n1(2)=n1(1)+2, n1(3)=n1(2)+3+3, n1(4)=n1(3)+2+2, n1(5)=n1(4)+1=14;在第6步之后, n1(k)=14(k≥6), 其余节点亦是如此。
3.2 有效性验证
在MATLAB平台上对本文中的微电网分布式经济调度算法进行测试。本文提供了3种典型情景的仿真计算分析: 情景1和情景2分别验证在不考虑出力约束和考虑出力约束下, 分布式经济调度算法是否与集中式经济调度算法一样, 能够在满足供需平衡的条件下, 收敛到最优解; 情景3验证算法应对负荷变动的能力。
采用集中式经济调度算法时, 若不考虑出力约束, 由式(12)可知该系统经济调度最优解为λ*=122.8181 $/MW。
3.2.1 情景1
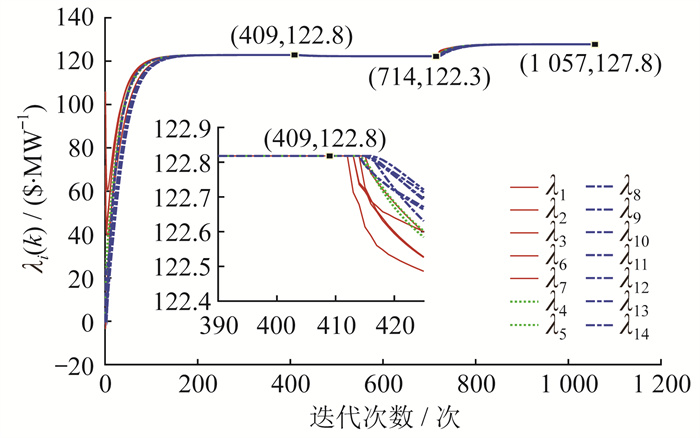
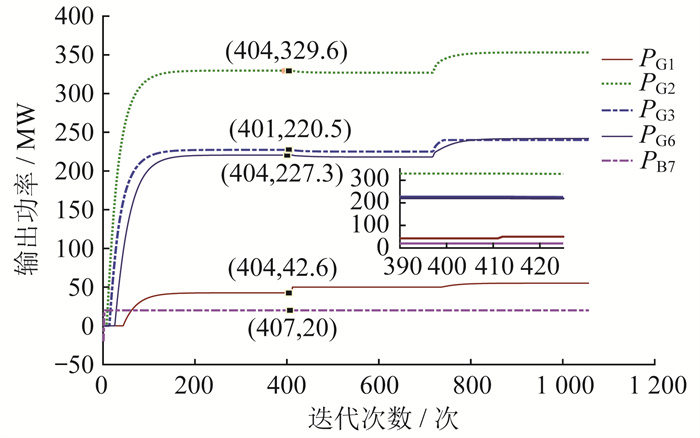
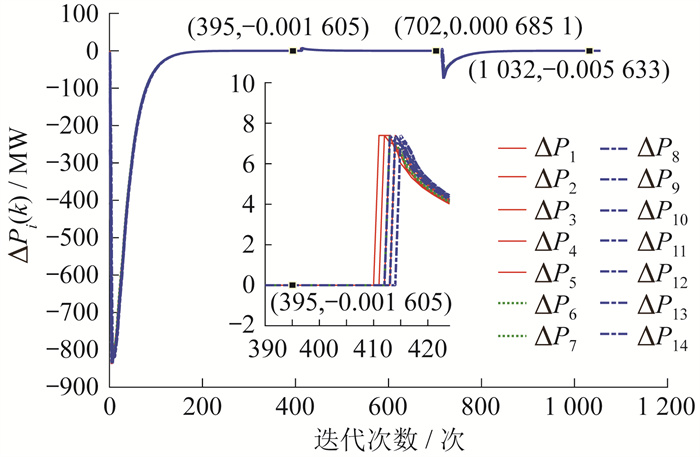
在不考虑出力约束的条件下, 测试系统非领导跟随模型一致性算法的微增成本变量、各发电单元和储能单元的输出功率以及各节点的局部功率缺额, 结果如图 2、图 3和图 4所示。其中, 取功率偏差δ=0.001。
根据仿真计算结果可知, 经过411次迭代之后, 各单元的微增成本变量均收敛于最优值122.818 1 $/MW。此时, 各发电单元和储能单元的输出功率分别为PG1=46.601 2 MW, PG2=329.614 4 MW, PG3=227.297 7 MW, PG6=220.297 7 MW, PB7=20 MW。各节点局部功率缺额在411次迭代之后非常接近于零, 说明情景1下本文所提算法达到了供需平衡。以上仿真结果显示, 分布式经济调度取得了与集中式经济调度相同的结果。
3.2.2 情景2
考虑各个发电单元的出力约束, 并取δ=0.000 5。由于之前发电单元SG1的输出功率已超出下限, 相应地, 其他发电单元的微增成本变量将减小。经过715次迭代之后, 微增成本变量再次收敛于最优值122.253 2 $/MW, 该数值也与集中式经济调度的数值相同。此时, PG1=50.000 0 MW, PG2=326.936 7 MW, PG3=225.017 3 MW, PG6=218.046 4 MW, PB7=20 MW。各节点局部功率缺额在715次迭代之后再次收敛于零, 再次说明本文所提算法达到了供需平衡。
3.2.3 情景3
将系统中各节点的负荷需求较正常运行时增加10%, 即总负荷变为PD=935 MW, 风机的输出功率提高为25 MW。因系统总需求增加, 所有节点的微增成本变量再次增加, 经过1 057次迭代之后, 再次收敛于127.766 6 $/MW。此时, PG1=55.062 7 MW, PG2=353.074 5 MW, PG3=240.000 0 MW, PG6=241.860 2 MW, PB7=20 MW。各节点局部功率缺额在1 057次迭代之后再次收敛于零, 同样说明本文所提算法达到了供需平衡。
3.3 与领导跟随模型一致性算法的比较
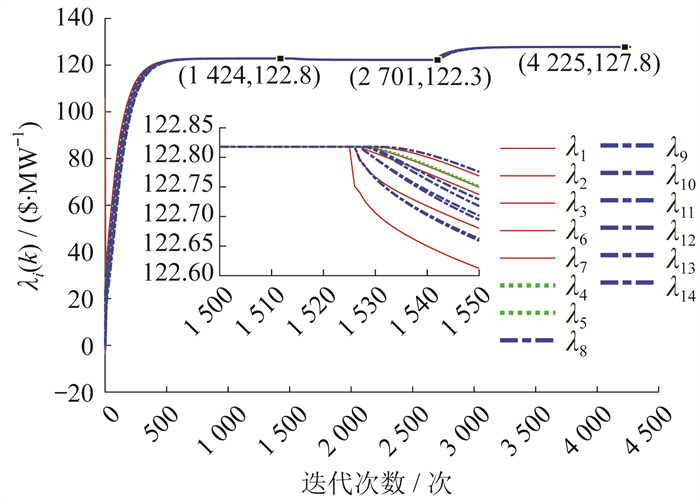
选取节点6作为领导者, 将领导跟随模型一致性算法[7]中的小参数设置为式(13)中各节点小参数的平均值0.009, 通过仿真计算得到微增成本变量如图 5所示。
对比前文数据可以得出: 情景1下, 算法的微增成本变量在1 524次迭代后收敛于122.818 0 $/MW, 本文所提算法在411次迭代后收敛, 收敛速度提高了约2.7倍。情景2下, 算法在2 700次迭代后收敛于122.253 2 $/MW, 而本文算法在715次迭代后收敛; 情景3下, 算法在4 275次迭代后收敛于127.766 9 $/MW, 而本文算法在1 057次迭代后收敛。
从仿真结果可看出, 与已有领导跟随模型的分布式经济调度策略相比, 本文算法不但可以收敛于相同的最优解, 同时收敛速度明显较快。
4 结语
基于一致性理论, 本文提出了一种微电网分布式多目标经济调度算法。该算法有如下3个特征: 利用机器人系统的工作模式获取局部功率缺额, 解决了全局信息获取困难这一问题; 算法中的反馈小参数由分布式算法提供, 可以动态更新, 不需要提前给定; 不需要设置发电单元的输出功率初值之和与负荷相等, 可以灵活应对系统负荷变动的情况, 实现了真正的完全分布式。算例分析结果表明, 该算法对发电单元出力约束和系统负荷变动等问题具有良好的鲁棒性。
参考文献
-
[1]LIN C E, VIVIANI G L. Hierarchical economic dispatch for piecewise quadratic cost functions[J]. IEEE Transactions on Power Apparatus and Systems, 1984(6): 1170-1175.
-
[2]陈厚合, 王子璇, 张儒峰, 等. 含虚拟电厂的风电并网系统分布式优化调度建模[J]. 中国电机工程学报, 2019, 39(9): 2615-2624. DOI:10.13334/J.0258-8013.PCSEE.181059
-
[3]BINETTI G, ABOUHEAF M, LEWIS F, et al. Distributed solution for the economic dispatch problem[C]//21st Mediterranean Conference on Control and Automation. Platanias: IEEE, 2013: 243-250.
-
[4]谢俊, 陈凯旋, 岳东, 等. 基于多智能体系统一致性算法的电力系统分布式经济调度策略[J]. 电力自动化设备, 2016, 36(2): 112-117.
-
[5]刘春涛, 宋运忠. 基于负荷均衡加载的电力系统分布式经济调度策略[J]. 电力系统保护与控制, 2022, 50(20): 139-148.
-
[6]CHEN G, ZHAO Z Y. Delay effects on consensus-based distributed economic dispatch algorithm in microgrid[J]. IEEE Transactions on Power Systems, 2018, 33(1): 602-612. DOI:10.1109/TPWRS.2017.2702179
-
[7]ZHANG Z A, CHOW M Y. Incremental cost consensus algorithm in a smart grid environment[C]//2011 IEEE Power and Energy Society General Meeting. Detroit: IEEE, 2011: 1-6.
-
[8]邵雪莲, 陈珍萍, 付保川, 等. 考虑柔性负荷的微电网快速一致性多目标调度[J]. 现代电子技术, 2022, 45(3): 135-141. DOI:10.16652/j.issn.1004-373x.2022.03.025
-
[9]卢梦蝶, 宁涛, 王德佳, 等. 基于多智能体一致性的多微电网分布式经济调度[J]. 电气自动化, 2022, 44(2): 21-24.
-
[10]乐健, 周谦, 赵联港, 等. 考虑个体欺骗的有源配电网完全分布式经济调度策略[J]. 中国电机工程学报, 2020, 40(17): 5445-5453.
-
[11]YANG S P, TAN S C, XU J X. Consensus based approach for economic dispatch problem in a smart grid[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4416-4426.
-
[12]阮博, 俞德华, 李斯吾. 基于一致性的微网分布式能量管理调度策略[J]. 电力系统保护与控制, 2018, 46(15): 23-28.
-
[13]米阳, 彭建伟, 陈博洋, 等. 基于一致性原理和梯度下降法的微电网完全分布式优化调度[J]. 电力系统保护与控制, 2022, 50(15): 1-10.
-
[14]BINETTI G, DAVOUDI A, LEWIS F L, et al. Distributed consensus-based economic dispatch with transmission losses[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1711-1720.
-
[15]HUG G, KAR S, WU C Y. Consensus + innovations approach for distributed multiagent coordination in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1893-1903.
-
[16]徐豪, 张孝顺, 余涛. 非理想通信网络条件下的经济调度鲁棒协同一致性算法[J]. 电力系统自动化, 2016, 40(14): 15-24.
-
[17]张子泳, 仉梦林, 李莎. 基于多目标粒子群算法的电力系统环境经济调度研究[J]. 电力系统保护与控制, 2017, 45(10): 1-10.
-
[18]王晓玲. 二氧化硫税的国际比较及在减排中的作用评析[J]. 涉外税务, 2002(5): 49-52.
-
[19]孙静, 于继来. 节能发电调度问题的多目标期望控制模型及解法[J]. 电力系统自动化, 2010, 34(11): 23-27.
-
[20]冯昌森, 谢方锐, 文福拴, 等. 基于智能合约的绿证和碳联合交易市场的设计与实现[J]. 电力系统自动化, 2021, 45(23): 1-11.