光储微电网独立运行时, 光伏发电单元和储能单元通过输出功率来满足负荷的功率需求。但是, 光伏发电存在不稳定、平衡功率难度大、影响电能质量等问题^[1-3]。系统内负荷的波动也会对微电网的稳定运行带来挑战。研究发现, 通过对系统内变换器采取有效控制策略可以保证系统的电压频率稳定^[4-5]。

对微电网逆变器采用适当的控制策略是保证系统安全稳定运行的基础。对于光伏逆变器, 通常采用恒功率控制策略保证稳定的功率输出。文献[6-7]采用改进的光伏逆变器控制策略提高系统的电能质量。为实现分布式发电机组之间负荷的合理分配, 储能逆变器通常采用下垂控制策略^[8]。文献[9-10]提出自适应的虚拟阻抗用于分配非线性负载的无功功率。文献[11]通过将虚拟阻抗与二次控制相结合, 实现了不匹配馈线阻抗的功率合理分配。以上控制策略都基于PI环节来维持微电网的功率稳定, 但是其控制结构复杂, 有多个反馈回路, 导致动态响应速度慢。

在现有的微电网研究中, 通常没有考虑可再生能源的间歇性, 从实际应用的角度, 必须考虑能源的间歇性, 传统的线性级联控制不能有效应对这种波动, 因此需要更先进的控制方法来确保微电网系统稳定运行。

近年来, 模型预测控制(Model Predictive Control, MPC)被广泛应用于微电网的控制策略中^[12]。在逆变器控制领域, 根据控制时域的不同, MPC可以分为连续状态的连续集模型预测控制(Continuous Control Set-MPC, CCS-MPC)和离散状态的有限集模型预测控制(Finite Control Set-MPC, FCS-MPC)。相比于CCS-MPC, FCS-MPC无需脉冲宽度调制(Pulse Width Modulation, PWM)环节, 且利用了逆变器的离散特性和开关状态有限等特点, 在电力电子系统中得到了广泛关注。相比于PI调节的滞后性, FCS-MPC采用主动预测方法, 能显著提高储能系统的动态响应速度。文献[13]提出了利用FCS-MPC策略控制储能系统的变换器来平滑光伏系统输出和稳定直流母线电压。文献[14]将FCS-MPC与下垂控制方法结合, 实现了并联逆变交流微电网的控制, 但是该方法没有考虑新能源波动对系统的影响。文献[15]提出了一种多步预测的FCS-MPC算法, 在两个周期内保证了所选开关状态最优, 但是没有具体应用在微电网储能系统中。文献[16]采用分布式MPC方法对直流电网中风能和太阳能系统进行协调控制, 提高了系统的动态响应速度。文献[17]提出了一种不使用PI调节器的MPC策略, 通过基于模型预测电流控制电池储能系统的双向DC-DC变换器, 可以平滑可再生能源输出的波动, 同时保持稳定的直流电压, 采用模型预测电压控制对交直流联用变换器进行控制, 确保微电网与电网之间交流电压供应稳定, 功率流动正常。文献[18]提出了MPC策略来控制储能系统的变换器, 以平滑光伏输出和稳定直流总线电压。但文献[16-18]采用的MPC均未考虑在系统存在建模误差或面临较大扰动的情况下, 一个控制周期内的局部寻优算法可能导致控制系统不稳定的问题。

本文以独立运行的光储系统为研究对象, 提出一种考虑新能源波动的微电网MPC策略。对光储的DC-DC变换器采用稳压控制, 使储能系统和光伏系统输入逆变器前的电压都稳定在参考值; 对储能逆变器的内环搭建预测模型, 并在目标函数中考虑了多步预测, 提高了FCS-MPC算法精度以及系统的稳定性。改进后的方法继承了传统FCS-MPC动态性能良好的特点, 解决了传统PI控制动态速度响应慢的问题, 改善了系统受到较大扰动或建模存在误差时所造成的预测偏差的问题。

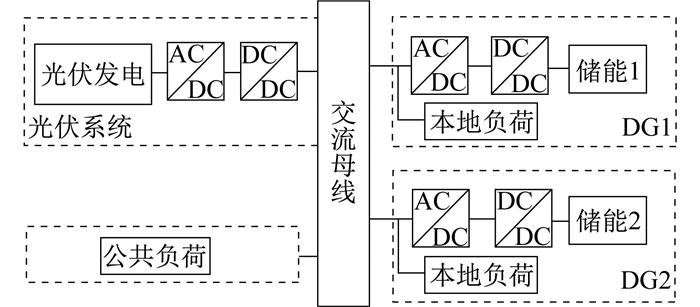
图 1为本文所研究的光储微电网系统结构, 包含光伏系统、储能系统以及负荷, 各分布式电源经过逆变器接在0.38 kV额定电压的交流母线上。其中, DG1、DG2表示储能系统。

光伏电池输出功率受天气影响较大, 为了保证系统的稳定性, 采用最大功率或恒定的功率输出, 因此本文中光伏系统采用基于最大功率点跟踪(Maximum Power Point Tracking, MPPT)稳压的PQ(恒功率)解耦控制。储能系统的DC-DC变换器采用稳压控制策略, AC-DC逆变器采用下垂控制与MPC相结合的控制方式, 实现对负荷功率的合理分配来维持系统电压频率稳定。

在微电网系统中, 忽略系统的能量损耗, 上述系统输出功率之间的关系式如下

$P_{\text {load }}=P_{\text {bat }}+P_{\mathrm{PV}}$

(1)

式中: P_load——负荷功率;

P_bat——储能系统输出功率;

P_PV——光伏系统输出功率。

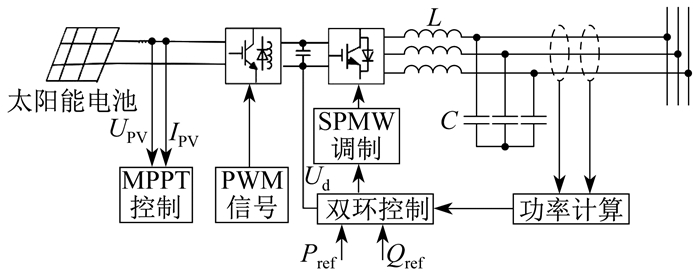
本文采用的光伏系统控制框图如图 2所示。其中: U_PV、I_PV分别为光伏电池输出的电压和电流; P_ref和Q_ref分别为有功功率和无功功率参考值; L和C分别为滤波电感和滤波电容; U_d为测量到的直流电压; SPMW为正弦波脉宽调制(Sine Wave Pulse Width Modulation)。光伏阵列先通过DC-DC变换器升压, 并采用MPPT控制实现对光伏电池输出功率的控制; DC-AC逆变器采用PQ控制策略为负载提供稳定的功率输出。采用MPPT控制和PQ控制结合可以提高系统控制的准确度以及光伏发电的利用率。其中, MPPT控制采用扰动观察法, 通过给予输出电压小扰动观测输出功率的变化趋势进而不断调整电压, 使光伏系统输出功率达到最大值。

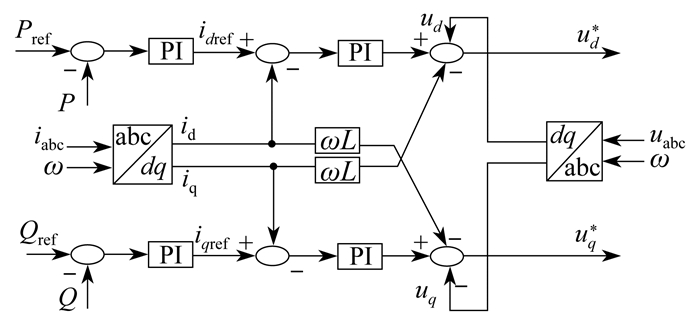
PQ控制器由功率外环和电压电流双环构成, 其控制框图如图 3所示。其中, i_dref、i_qref分别为d轴、q轴电流参考值; u_d^*、u_q^*分别为d轴、q轴电压参考值; i_d、i_q分别为d轴、q轴电流; u_d、u_q分别为d轴、q轴电压; u_abc、i_abc分别为三相电压、电流; P、Q分别为光伏系统有功、无功功率实际值; ω为系统的角频率。

图 3中, 令电压矢量与d轴保持同一方向, 所以q轴电压分量为零, 可以得到电流参考值为

$\left\{\begin{array}{l}i_{d \mathrm{ref}}=\frac{2 P_{\mathrm{ref}}}{3 u_d} \\ i_{q \mathrm{ref}}=-\frac{2 Q_{\mathrm{ref}}}{3 u_d}\end{array}\right.$

(2)

将参考电流与实际电流做差后进行PI控制, 并考虑了交叉前馈补偿和电压前馈补偿, 得到SPWM调制电压信号, 输出稳定的有功、无功功率。其中d轴和q轴电压的方程如下

$\left\{\begin{array}{l}u_d^*=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(i_{d \mathrm{ref}}-i_d\right)-\omega L i_q+u_d \\ u_q^*=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(i_{q \mathrm{ref}}-i_q\right)-\omega L i_d+u_q\end{array}\right.$

(3)

式中: k_p、k_i——PI控制器比例、积分环节系数。

储能系统的DC-DC变换器采用稳压控制策略, 可以将输入到逆变器的电压维持在固定值, 有利于维持系统稳定。

储能稳压控制框图如图 4所示。储能系统采用电压外环电流内环的双环控制策略, 将参考值U_{dc_ref}与实际值U_dc做差之后通过PI控制器, 再经过限幅环节得到电流参考值, 再与电流实际值I_b做差之后通过PI控制器得到变换器的输入信号。

对于孤岛微电网来说, 储能逆变器的控制目标是为负载建立稳定和平衡的输出电压。下垂控制无需通信环节, 当负荷变化时可以快速准确地分配各个储能的功率, 使系统达到安全稳定的运行状态。

储能逆变器采用双环控制方式。通过采集电感电流和电容电压进行功率计算, 得到有功、无功功率实际值; 由式(4)计算电压、频率的参考值U、f, 再经过限幅环节以及三相电压合成得到电压参考值。

$\left\{\begin{array}{l}U=U^*-n_j \cdot\left(Q_j-Q^*\right. \\ f=f^*-m_j \cdot\left(P_j-P^*\right)\end{array}\right.$

(4)

式中: U^*——额定电压;

n_j、m_j——电压和频率的下垂控制斜率, j为DG1和DG2的逆变器, j=1, 2;

Q_j——平均无功功率;

Q^*——额定无功功率;

f^*——额定频率;

P_j——平均有功功率;

P^*——额定有功功率。

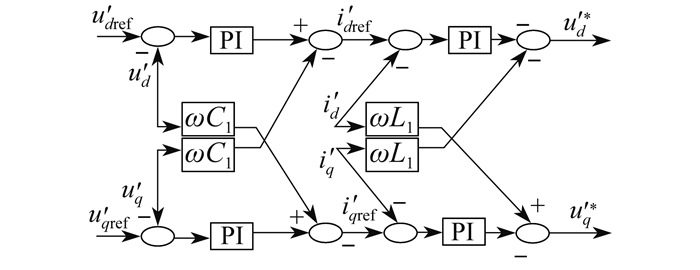
电压电流双闭环控制框图如图 5所示。

该框图包括电压外环以及电流内环, 目的是实现逆变器输出电压对参考电压的跟踪, 提高系统的动态响应性能。首先, 采集逆变器输出端的电压电流信息, 经dq变换模块后, 转换为i′_d, i′_q, u′_d, u′_q 4个分量。其次, 将电压解耦后与各自参考值做差经过PI环节(k_p+k_i/s)以及电容解耦环节(-ωC₁u′_q和ωC₁u′_d)以提高控制响应速度, 得到内环电流控制需要的参考电流i′_dref与i′_qref。最后, 将参考电流与实际电流做差后进行PI控制, 并加入(ωL₁i′_d和-ωL₁i′_q), 得到PWM调制信号u_d^′*、u_q^′*, 对逆变器进行控制。分析可得

$\left\{\begin{array}{l}i_{d \text {ref}}^{\prime}=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(u_{d \mathrm{ref}}^{\prime}-u_d^{\prime}\right)-\omega C_1 u_q^{\prime} \\ i_{q \text {ref}}^{\prime}=\left(k_{\mathrm{p}}+\frac{k_i}{s}\right)\left(u_{q \mathrm{ref}}^{\prime}-u_q^{\prime}\right)+\omega C_1 u_d^{\prime}\end{array}\right.$

(5)

$\left\{\begin{array}{l}u_d^{\prime *}=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(i_{d \mathrm{ref}}^{\prime}-i_d^{\prime}\right)-\omega L_1 i_q^{\prime} \\ u_q^{\prime *}=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(i_{q \mathrm{ref}}^{\prime}-i_q^{\prime}\right)+\omega L_1 i_d^{\prime}\end{array}\right.$

(6)

P-f、Q-U的下垂控制策略控制结构复杂, 有多个反馈回路和PWM调制环节, 导致动态响应速度慢, 而且, PI参数整定费时, 使得控制器效果不容易实现。在微电网系统出现功率波动时, 由于微电网的抗干扰能力较弱, 需要储能系统具有快速响应的能力, 因此需要提高储能系统的调节速度。

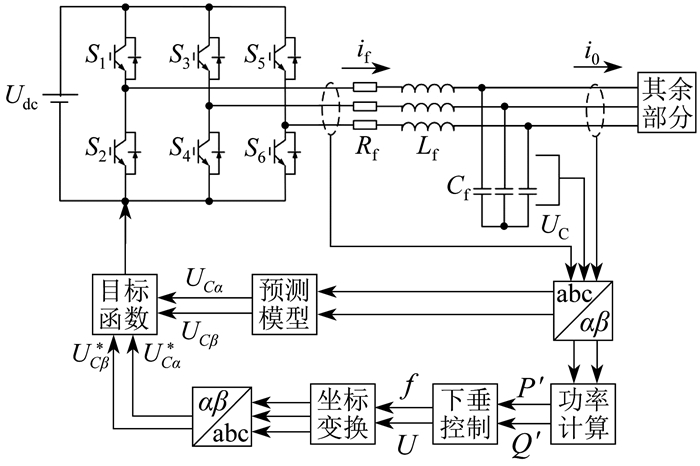
模型预测控制采用逆变器的离散模型。由于逆变器的开关状态数量很少, 因此MPC优化问题可以简化为仅预测可能的开关状态来预测系统的状态行为, 使用滤波器来预测所有可能的控制输入的结果, 在有限的时间步长内达到最小的目标函数。将模型预测方法应用在储能系统变换器控制中, 利用其预测能力可以达到使系统快速响应并稳定运行的目标。图 6为储能逆变器MPC控制结构图。其中, U_Cα^*、U_Cα、U_Cβ^*、U_Cβ分别为电容电压的实分量、虚分量的参考值和实际值, P′、Q′分别为储能系统的有功、无功功率实际值。三相LC滤波器连接到逆变器的输出端来抑制开关产生的谐波。滤波器的每个支路包括一个电感L_f和串联电阻R_f的电感器和一个电容C_f的电容。i₀为三相LC滤波器的输出电流。i_f为流过L_f的电感电流, U_C为流过C_f的电容电压。

逆变器有3个分支, 每个分支包含2个开关, 即S₁~S₆, 可以使用数字1和0分别表示它们的开关状态。如果上开关断开, 另一个开关接通, 则为0;如果上开关接通, 另一个开关断开, 则为1。开关的动作影响逆变器的输出电压(U₀, U₁, U₂, …, U₇), 对应有8种可能的开关状态(000, 100, 110, 010, 011, 001, 101, 111)。逆变器的电压矢量U_i可以表示为

$\boldsymbol{U}_i= \begin{cases}\frac{2}{3} U_{\mathrm{dc}} \mathrm{e}^{\mathrm{j}(i-1) \frac{\pi}{3}} & (i=1, 2, 3, \cdots, 6) \\ 0 & (i=0, 7)\end{cases}$

(7)

由于U₀和U₇的输出电压结果相同, 可以忽略其中一个, 用7个矢量来控制逆变器。这些向量中的每一个都可以用来预测代价函数, 使代价函数最小的向量用于在下一个采样间隔内控制逆变器。

假设3个支路的参数值都相等, LC滤波器电容的动态行为可表示为

$\begin{aligned} & L_{\mathrm{f}} \frac{\mathrm{d} i_{\mathrm{f}}}{\mathrm{d} t}=U_i-U_C-R_{\mathrm{f}} i_{\mathrm{f}} \\ & C_{\mathrm{f}} \frac{\mathrm{d} U_C}{\mathrm{~d} t}=i_{\mathrm{f}}-i_0\end{aligned}$

(8)

式中: U_i——逆变器电压矢量的模值。

在式(8)中, 将i₀视为扰动变量, 可由电流传感器测量或由观测器估计得出, i_f和U_C为状态变量, U_i为控制信号。根据式(8), 离散时间内的数学模型可以表示为

$\boldsymbol{x}(k+1)=\boldsymbol{A}_{\mathrm{d}} \boldsymbol{x}(k)+\boldsymbol{B}_{\mathrm{d}} \boldsymbol{u}(k)$

(9)

其中:

$\left\{\begin{array}{l}\boldsymbol{x}(k+1)=\left[\begin{array}{l}i_{\mathrm{f}}(k+1) \\ U_C(k+1)\end{array}\right] \\ \boldsymbol{u}(k)=\left[\begin{array}{c}U_i(k) \\ i_0(k)\end{array}\right] \\ \boldsymbol{A}_{\mathrm{d}}=\mathrm{e}^{\boldsymbol{A} T_{\mathrm{s}}} \\ \boldsymbol{B}_{\mathrm{d}}=\int_0^{T_{\mathrm{s}}} \mathrm{e}^{\boldsymbol{A} \tau} \boldsymbol{B} \mathrm{d} \tau \\ \boldsymbol{A}=\left[\begin{array}{cc}\frac{-R_{\mathrm{f}}}{L_{\mathrm{f}}} & \frac{-1}{L_{\mathrm{f}}} \\ \frac{1}{C_{\mathrm{f}}} & 0\end{array}\right] \\ \boldsymbol{B}=\left[\begin{array}{c}\frac{1}{L_{\mathrm{f}}} \\ 0\end{array}\right]\end{array}\right.$

(10)

式中: T_s——采样周期。

在MPC中, 目标函数用于选择适当的控制信号。由于孤岛微电网需要对输出电压进行控制, 因此目标函数定义为电容电压跟踪误差的二次函数, 以选择合适的控制信号。目标函数g₁可设置为

$g_1=\left[U_{C\alpha}^*-U_{C \alpha}(k+1)\right]^2+\left[U_{C\beta}^*-U_{C \beta}(k+1)\right]^2$

(11)

式中: U_Cα(k+1)、U_Cβ(k+1)——k+1时刻电容电压的实分量和虚分量。

其中电压的参考值是由下垂控制得到的。在此目标函数的基础上, 在下一个采样周期中应用使g₁值最小的电压向量。由于α和β分别被独立控制, U_C可以跟踪参考值。

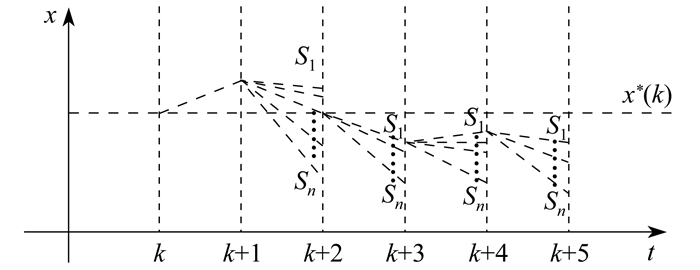
在实际计算过程中, 当系统存在建模误差或发生大扰动时, 在第k个采样周期内计算出的最优开关状态, 应用到k+1时刻可能并不是使目标函数最小的开关状态, 但是在k时刻确定的开关状态在k+1时刻仍继续使用, 从而导致预测值偏离参考值。单步预测的传统MPC原理如图 7所示。

图 7中, 系统在k+2时刻虽然达到了最优状态, 但是k+2时刻输出的开关状态均未穿越给定的参考值x^*(k), 因此在k+4时刻, 系统发生发散, 偏离参考值更远。

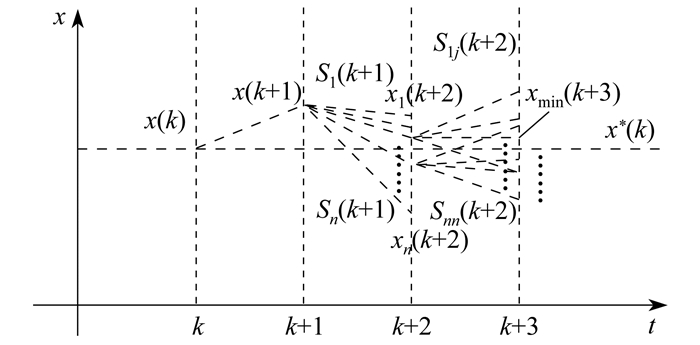
预测步数太少会导致跟踪精度不够, 但预测步数越多, 控制器计算量就越大, 因此本文取储能电压的二步长预测值加入目标函数。采用两步预测控制, 在k+1时刻计算出使k+3时刻目标函数最小的开关状态, 并在k+2时刻应用, 同时保留一步预测的目标函数, 提高模型预测控制精度。多步预测MPC原理如图 8所示。

通过预测未来两个时刻的预测值选择最优输出状态, 保证了系统在两个控制周期内所选输出状态最优。因此, 多步预测的目标函数g_con如下:

$\begin{aligned} g_{\text {con }}= & {\left[U_{C \alpha}^*-U_{C \alpha}(k+1)\right]^2+\left[U_{C \beta}^*-U_{C \beta}(k+1)\right]^2+} \\ & {\left[U_{C \alpha}^*-U_{C \alpha}(k+2)\right]^2+\left[U_{C \beta}^*-U_{C \beta}(k+2)\right]^2 }\end{aligned}$

(12)

在MATLAB/Simulink中进行仿真测试, 选取蓄电池模型, 设置参考电压为400 V。按照上述稳压控制策略搭建DC/DC变换器及其控制模块, 设置仿真时间为1 s, 输出电压波形如图 9所示。由图 9可以看出, 通过稳压控制调节储能输出电压, 在0.07 s左右便维持在了400 V, 具有快速的响应特性, 稳定效果良好。

在Simulink中搭建光伏系统的仿真模型, 设置初始光照强度为2 kW/m², 温度为25 ℃。在0.5 s时提高光照强度至2.5 kW/m², 1 s时提高温度至30 ℃, 仿真时间设置为1.5 s。仿真测试结果如图 10所示。

由图 10可知, 在不到0.1 s的时间内, MPPT控制实现了最大功率的跟踪, 跟踪速度良好, 同时当外界条件发生变化时, 在不到0.01 s的时间内MPPT控制实现了准确跟踪, 灵敏度良好。

根据上述对光伏和储能系统逆变器的分析, 在Simulink仿真平台搭建光储微电网系统仿真模型。对传统的基于电压外环、电流内环的下垂控制, 基于传统MPC以及基于改进MPC的储能逆变器控制策略分别进行仿真分析, 验证控制策略的有效性。

联立式(2)、式(3)、式(5)、式(6)可以得到PQ控制和下垂控制的双环传递函数。设定储能逆变器参数电容C_f为1.5 mF, 电感L_f为0.6 mH。首先根据系统传递函数得到PI控制参数初值, 再基于经验法^[19], 通过实验最终确定电压外环、电流内环的PI参数。其中: 电压外环k_p=12, k_i=0.2;电流内环k_p=0.1, k_i=0.01。储能电池容量为350 Ah, 逆变器标准电压为380 V, 额定频率为50 Hz。同理, 根据传递函数和经验法得到: 光伏逆变器电压外环PI参数k_p=0.5, k_i=10;电流内环PI参数k_p=20, k_i=200。设定光照充足时光伏电池的输出功率大于10 kW, 光伏PQ控制参考有功功率设为10 kW, 参考无功功率设置为零。为了验证模型在负荷发生改变时的稳定能力, 2 s时, DG1的本地负载由(12 kW, 3 kVA)增加到(22 kW, 4 kVA), DG2的本地负载在4 s时由(23 kW, 9 kVA)下降到(13 kW, 2 kVA); 然后在3 s接通公共负载(15 kW, 14 kVA), 并在5 s切断。

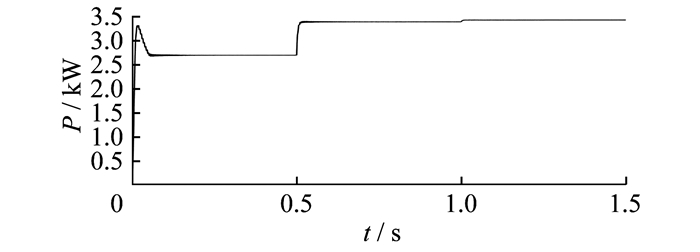
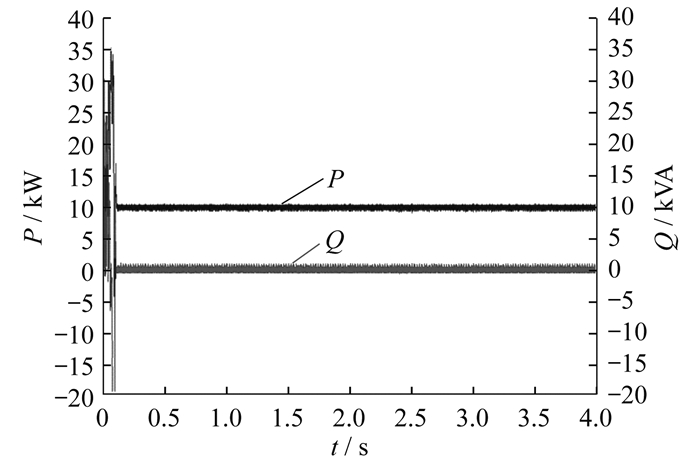
光伏系统PQ控制输出功率波形如图 11所示。

由图 11可知, 仿真开始阶段系统有一定波动, 在不到0.1 s的时间内完成调节, 输出恒定的有功、无功功率, 并且在负荷变化时, 仍能保持恒定的功率输出。

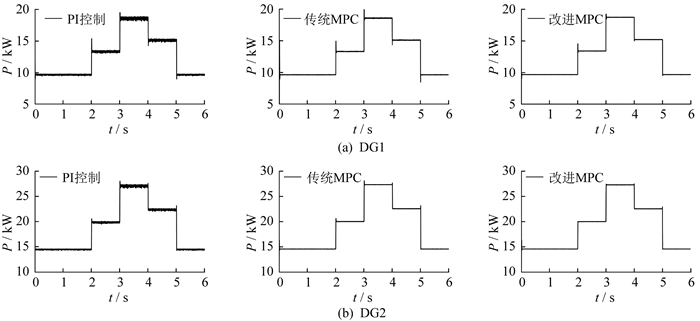
储能系统输出的有功功率如图 12所示。由图 12可以看出, 采用不同内环控制器下负荷功率的分配情况。通过连接和切断负荷, 体现了该方法的动态性能。相较于传统的PI控制, 采用MPC控制可以更为快速准确地分配负荷功率。相较于传统MPC控制, 采用多步长改进MPC控制可以减小系统最大偏差, 提高系统稳定性。

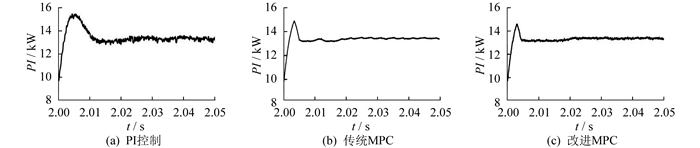
DG1输出的有功功率在2 s时的放大波形, 如图 13所示。由图 13可知: 基于PI控制的传统储能逆变器控制经过15 ms输出稳定的功率, 且最大输出功率偏差为2.5 kW; 传统MPC控制经过4 ms可以输出稳定的功率, 输出功率最大偏差为1.9 kW; 而改进MPC控制经过5 ms即可输出稳定的功率, 输出功率最大偏差为1.5 kW。与基于传统MPC的下垂控制策略相比, 多步长改进MPC控制策略减小了系统的最大偏差, 提高了系统的稳定性, 但略微增加了调节时间。与基于PI的传统双闭环控制相比, 多步长改进MPC控制下的储能系统的动态响应速度提升很大, 提高了系统平抑微电网功率波动的能力。由于储能系统输出无功功率呈现出类似规律, 因此不再绘制。

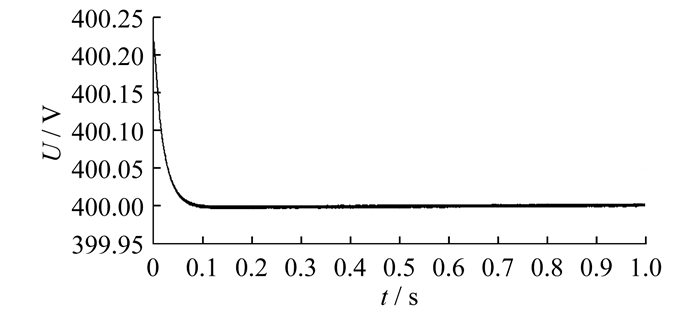
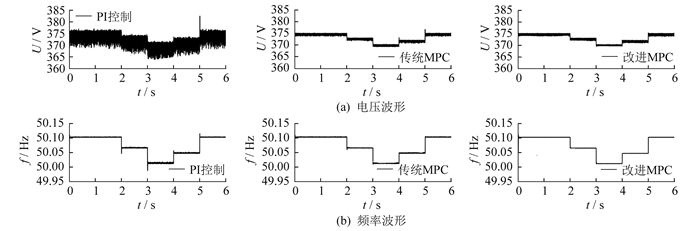
采用不同内环控制器时交流母线电压有效值和系统频率波形如图 14所示。

下垂控制会产生稳态误差, 使母线电压和频率不能恢复到初始状态。通过连接和切断负荷, 可检验各方法动态性能和控制策略的稳定性。由图 14可知, 负荷发生较大变化时, 电压和频率都能够迅速恢复到允许范围。因此, 本文所提控制策略对于各种敏感性负载负荷变化时, 电能质量能够符合要求。

本文针对传统PI双闭环控制存在动态响应速度不佳以及微电网稳定性差等问题, 提出了一种适用于孤岛储能逆变器的改进MPC方法。采用稳压控制策略, 保证输入逆变器的电压为恒定值, 减小输入电压波动对控制策略的影响, 对储能逆变器采用基于多步预测MPC的下垂控制, 实现对负荷功率的合理分配, 提高系统的动态响应速度和稳定性, 保证系统具有良好的电能质量。