|
|
|
发布时间: 2023-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-07-24
基金项目: 国家重点研发计划政府间项目(2019YFE0118400);济南市"新高校20条项目"(T202116)
中图法分类号: TM615
文献标识码: A
文章编号: 2096-8299(2023)06-0529-07
|
摘要
针对传统单一模型难以有效分析历史数据的波动性规律,从而导致光伏功率预测精度不高的问题,提出了一种基于核密度估计和CatBoost算法的超短期光伏功率预测方法。首先,采集相关的辐射、温度和湿度等特征量,创建光伏功率概率分布统计模型;其次,基于功率分布特性和CatBoost算法构建光伏电站功率预测模型;最后,将所提出的模型应用到实际算例中验证其有效性。通过与常用的预测算法对比,所提模型的预测误差相较于传统模型SVR、DTR、KNN、LSTM、LightGBM分别下降了27.59%、8.69%、16.21%、23.33%和12.56%。
关键词
光伏功率预测; CatBoost算法; 核密度估计
Abstract
In order to address the problem of low accuracy in photovoltaic power forecasting caused by the difficulty of traditional single models in effectively analyzing the volatility patterns in historical data, this paper introduces a combination of the categorical boosting algorithm, kernel density estimation, and ultra-short-term photovoltaic power forecasting.Firstly, feature engineering is applied to extract the characteristic vectors of radiation, temperature and humidity related to the modeling, and the statistical model of photovoltaic power probability distribution is created.Secondly, based on the power distribution characteristics and CatBoost algorithm, the power prediction model of PV station is proposed.Finally, the mentioned model algorithm is applied to the actual site calculation to verify its effectiveness, and the comparison with the existing common prediction algorithms shows that the model proposed in this paper can effectively improve the prediction performance.Compared with the traditional models SVR, DTR, KNN, LSTM and Light GBM, the prediction error of SRMSE is decreased by 27.59%, 8.69%, 16.21%, 23.33% and 12.56%, respectively.
Key words
photovoltaic power forecasting; CatBoost method; kernel density estimation
太阳能是一种取之不尽的清洁能源, 光伏发电是太阳能利用的有效形式之一。但是, 太阳能光伏发电具有波动性、随机性等缺点, 给并网光伏发电、建筑一体化光伏发电和分布式光伏发电等领域带来了设计及运行挑战, 严重影响了太阳能的利用效率, 限制了光伏发电的前景和发展规模。现有的解决方法包括光伏-储能组合优化运行技术、风光水储多能互补技术, 以及光伏功率预测等。其中, 有效的光伏功率预测在新能源系统的可靠性等方面起着重要作用。
集中式光伏功率预测有多种分类方式。按照预测过程, 光伏功率预测可分为直接预测和间接预测; 根据预测的空间尺度, 可分为单场预测和区域预测; 根据预测的时间尺度, 可分为超短期预测、短期预测、中期预测和长期预测; 根据预测的形式, 可分为确定性预测和概率性预测[1]。光伏功率的确定性预测主要是基于时间序列和气象因素, 通过建立数学模型来预测光伏发电的产量。为了分析时间序列对预测的影响, 文献[2]提出了一种基于卷神经网络(Convolutional Neural Networks, CNN)和长短期记忆(Long Short Term Memory, LSTM)网络的混合模型。该方法指出, 合理的时间序列数据长度可以提高光伏预测精度、降低计算成本。文献[3]提出了2种新的太阳能光伏随机预测模型, 与标准时间序列预测机制相比, 总发电量有了显著提高。针对不同气象条件和季节下的短期光伏输出功率预测, 文献[4]提出了一种新的CNN模型, 模型设计为一个并行池结构, 提高了预测性能。文献[5]将增强碰撞刚体优化(Enhanced Colliding Bodies Optimization, ECBO)算法、变分模式分解(Variational Mode Decomposition, VMD)和深度极限学习机(Deep Extreme Learning Machine, DELM)相结合, 提出了一种基于相似日的光伏功率短期多步预测模型。文献[6]提出了一种多通道卷积神经网络, 利用代表各种区域效应的光栅图像数据预测每月光伏发电量。文献[7]提出了一种三阶段机器学习架构, 结合使用轻量级梯度提升机(Light Gradient Boosting Machine, LightGBM)和随机森林(Cuda Random Forest, CURF), 提高了模型性能。
与确定性预测相比, 光伏发电的概率性预测考虑了更多因素。概率性预测方法可以提供更多关于潜在不确定性的信息, 从而得到更全面的预测结果。在传统确定性预测方法的基础上, 文献[8]提出了一种光伏发电量的集成非参数概率预测模型, 将分位数回归平均(Quantile Regression Averaging, QRA)和LSTM结合, 获得光伏输出的概率预测。通过人工智能概率模型可以提高预测的可靠性。文献[9]提出了一种混合概率太阳辐照度预测方法, 结合了深度循环神经网络(Deep Recurrent Neural Network, DRNN)和残差建模。另外, 还有将物理光伏模型链扩展为概率预测的方法, 使用模型链的校准集合来生成概率光伏发电预测模型。文献[10]将模糊信息粒化(Fuzzy Information Granulation, FIG)、差分自回归移动平均(Autoregressive Integrated Moving Average, ARIMA)和改进的长短期记忆(Improved Long Short Term Memory, ILSTM)网络3个模型相结合, 构建了一个混合区间预测模型, 能够准确地覆盖实际光伏功率值。文献[11]提出了一种基于高阶马尔可夫链(Higher order Markov Chain, HMC)的光伏发电功率概率分布函数预测方法, 利用高斯混合法(Gaussian Mixture Method, GMM), 结合多个分布函数, 并使用基于HMC的模型系数对光伏功率进行超短期预测。
基于上述分析发现: 利用时间序列对太阳能光伏功率进行短期预测是有效的方法之一, 但当时间尺度和输出维度过多时, 预测结果反而并不理想。传统的预测方法主要基于物理和统计模型, 利用模型假设、系统参数和天气数据等进行预测, 通常需要大量的数据支撑, 在复杂气象条件下, 预测效果无法达到预期。为解决上述问题, 本文针对环境因素对光伏功率预测的影响进行研究, 深度解析各主要影响因素与光伏功率的耦合关联特性, 进而实现高精度和高可靠度的短期预测。首先, 使用核密度估计(Kernel Density Estimation, KDE)对光伏发电功率进行分析, 获得光伏发电功率的分布概率; 其次, 通过CatBoost算法对功率与各影响因素之间的非线性耦合相关性进行研究, 运用CatBoost预测模型对光伏发电功率变化趋势进行预测; 然后, 构建基于CatBoost和KDE的超短期光伏功率预测框架, 进一步提高光伏功率预测的精度和可靠性; 最后, 给出系统参数和算例结果分析。
1 功率预测模型的构建
1.1 KDECatBoost预测模型
KDE属于非参数检验方法。在光伏功率预测中, KDE可用于功率数据的建模和分析。它能够提供功率的概率分布信息, 有助于了解功率的变化范围和分布情况, 从而为决策提供更全面的依据[12]。
CatBoost与极端梯度提升(Extreme Gradient Boosting, XGBoost)和LightGBM是梯度提升决策树(Gradient Boosting Decision Tree, GBDT)的3种主要算法, 相对于XGBoost和LightGBM, CatBoost的准确率更高。CatBoost能够处理分类特征和缺失数据, 具有较强的泛化能力, 并且可以自动处理类别型特征的编码, 减少特征工程的复杂性。另外, CatBoost还能够自动进行特征选择和调参, 提供较好的模型性能。由于其采用完全对称树作为基模型, 故可以避免过拟合, 提高预测的可靠性, 强大的泛化能力和自动调参功能, 使得其成为光伏功率预测的有力工具。
为了提高预测的准确度, 本文利用KDE分析特征数据, 研究光伏功率分布概率特性, 同时利用CatBoost在非连续性类别特征处理和运算速度方面的优势, 将光伏功率分布概率预测结果输入CatBoost模型中, 得到最终的光伏功率预测结果。
1.2 特征处理
1.2.1 KDE特征处理
非参数KDE是利用观测数据对某事件进行密度函数估计。其过程就是将每一点的概率分配到附近的区间, 将所有的独立点区间密度累加, 即可得到最终的密度函数。假设X1, X2, X3, …, Xq是从总体中抽取的q个独立同分布样本, 其密度函数为f(x), 则KDE公式为
| $\hat{f}(x)=\frac{1}{q h} \sum\limits_{i=1}^q K\left(\frac{x-X_i}{h}\right)$ | (1) |
式中:
x——数据样本;
h——带宽;
K(x)——核函数。
带宽h是影响整个拟合效果优劣的核心因素[13]。由式(1)可以看出: 若h的取值较大, 则样本数据经过压缩处理突出了平均化, 忽略了密度函数的细节部分; 若h的取值较小, 则随机性的影响增大, 估计曲线尖峰过多, 函数图像波动大。为判断预测的光伏功率分布是否符合实际分布, 将光伏功率数据划分为m组不重复的数据, 采用拟合优度检验, 公式为
| $\chi^2=\sum\limits_{i=1}^m \frac{\left(A_i-E_i\right)^2}{E_i}$ | (2) |
式中: χ2——拟合优度检验结果;
Ai——光伏功率在第i个区间的观测频数;
Ei——光伏功率在第i个区间的期望频数。
1.2.2 Catboost特征处理
利用CatBoost对常规离散特征方法进行优化, 通过添加先验分布项使数据免受噪声和低频率类别型数据的干扰。这一优化过程的具体公式为
| $x_{i, k}=\frac{\sum\limits_{x_{i, j \in D_k}}\left[x_{i, k}=x_{i, j}\right] Y_j+a p}{\sum\limits_{x_{i, j \in D_k}}\left[x_{i, k}=x_{i, j}\right]+a}$ | (3) |
式中: xi, k——第k个样本的第j个类别特征;
xi, j——第k个样本之前第j个样本的第i个类别特征;
Dk——随机排序中在第k个样本之前的数据集;
Yj——第j个样本的标签值;
a——权重系数;
p——添加的先验分布项。
2 预测流程及性能评估
2.1 预测流程
本文提出的KDE-CatBoost光伏功率预测模型步骤如下。
步骤1 数据获取。采集集中式光伏电站的历史光伏功率和历史气象数据。
步骤2 数据预处理。检测数据中的异常值和缺失值, 剔除缺失值, 采用前后数据求平均值的方式处理异常值, 并对数据进行归一化处理。归一化公式为
| $x_i^{\prime}(k)=\frac{x_i(k)-x_{i, \min }}{x_{i, \max }-x_{i, \min }}$ | (4) |
式中: x′i(k)——第i个类别特征的第k个归一化值;
xi(k)——第i个类别特征的第k个原始值;
xi, min、xi, max——第i个类别特征的最小值和最大值。
步骤3 建立数据集。该数据集包含目标变量(即光伏功率)和特征变量(即气象因子)。
步骤4 数据分析。对各数据进行相关性分析, 并通过KDE方法确定符合条件的特征数据及种类。
步骤5 数据集拆分。将辐射、温度、气压、湿度、功率等数据拆分为训练集和测试集, 其中80%为训练集, 20%为测试集。
步骤6 构建CatBoost功率预测模型。为了使模型保持较高的预测精度, 通过经验设置和实验的方法调节模型参数。
步骤7 预测结果输出。将步骤6的预测结果进行反归一化, 得到最终预测结果。反归一化公式为
| $x=x_i^{\prime}\left(x_{\max }-x_{\min }\right)+x_{\min }$ | (5) |
式中: x——反归一化预测值;
x′i——归一化预测值;
xmin、xmax——光伏实际功率的最小值和最大值。
2.2 预测精度评估
本文采用多种评判方式对模型预测精度进行评估。主要评价指标包括平均绝对误差SMAE、均方误差SMSE、均方根误差SRMSE、决定系数SR2(R表示决定系数)。其计算公式分别为
| $S_{\mathrm{MAE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i-\hat{y}_i\right|$ | (6) |
| $S_{\mathrm{MSE}}=\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2$ | (7) |
| $S_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2}$ | (8) |
| $S_{R^2}=1-\frac{\sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}{\sum\limits_{i=1}^n\left(\bar{y}_i-y_i\right)^2}$ | (9) |
式中: n——预测值个数;
yi——第i时刻的实际采集数据;
y———实际采集数据的平均值。
3 算例分析
本文算例数据采用山东某地区光伏电站2017年4月—6月的信息, 数据间隔为15 min, 预测目标是大型集中式光伏电站提前1 h的功率。预测模型包含9个字段, 其中参与机器学习建模的变量有8个, 分别为总辐射、直辐射、散辐射、温度、环境温度、气压、环境湿度和光伏功率。
3.1 确定最佳KDE模型
对光伏功率进行KDE, 创建Kernel Density对象模型, 通过数据训练判定各样本的得分, 使用不同带宽和核函数进行测试, 观察不同带宽和核函数对密度估计的影响。
首先对不同的核函数进行计算, 然后选取预测概率密度最为接近的核函数, 最后计算最佳带宽值。但是, 在系统计算过程中, 一些测试点会发生偏移, 导致余弦、线性和Top-hat核函数执行错误。因此, 本文通过编写自定义函数的算法程序忽略测试点并返回平均值, 即可有效解决该问题。此外, 对函数进行优化和误差分析可得到最终的KDE图, 以及相应的最佳带宽和核函数参数。
为了更好地评估模型的拟合度优劣, 本文提出了模型优度指标。计算公式为
| $S_{\mathrm{GOF}}=\frac{1}{m} \sum\limits_{i=1}^m \frac{\left(\hat{y}_i-y_i\right)^2}{\left(\bar{y}_i-y_i\right)^2}$ | (10) |
式中: SGOF——模型优度指标, SGOF越接近于零说明模型拟合度越高;
m——预测样本数。
3.2 模型结果和误差分析
KDE模型、基于概率函数(Probability Function, PF)预测模型和非参数概率估计(Non-Parametric Probability Weighted Estimation, NP-PWE)预测模型的SRMSE、SGOF与χ2检验结果如表 1所示。
表 1
3种模型的预测误差
| 模型名称 | SRMSE | SGOF | χ2 |
| KDE | 0.007 9 | 0.006 5 | 5.36 |
| PF | 0.018 3 | 0.016 7 | 145.45 |
| NP-PWE | 0.009 2 | 0.009 6 | 20.58 |
由表 1可知, 基于PF的光伏功率分布预测模型SGOF较大且未通过χ2检验; KDE和NP-PWE模型的χ2都小于临界值, 但KDE模型的SGOF与χ2值更小, 即预测值与相应实际值更接近。相较于其他两种模型, KDE模型的SRMSE值最小。
3.3 光伏电站运行数据相关性分析
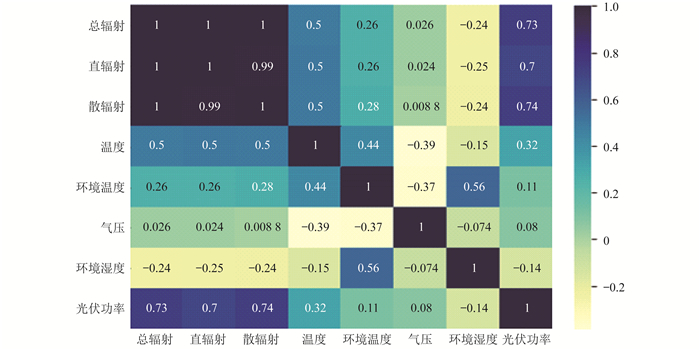
光伏电站运行数据的相关性系数如图 1所示。其中, 正数为正相关, 负数为负相关, 绝对值越大相关性越强。
由图 1可以看出, 辐射照度(总辐射、直辐射和散辐射)是光伏功率的主要影响因素之一。较高的辐射照度通常意味着更高的光能转换效率, 从而产生更高的光伏功率。
分析图 1中数据可知, 在一定范围内, 随着温度的升高, 光伏模块的电子特性和效率会发生变化, 从而影响光伏功率的输出。一般情况下, 光伏功率与温度之间存在负相关关系。但由于本文采集的数据中温度未达到对发电效率产生负影响的临界值, 故为正相关。
除了辐射照度和温度, 其他天气条件如云量、风速等也会对光伏功率产生影响。云量的增加和风速的提高可能导致日照减弱或局部阴影, 从而降低光伏功率。由于太阳高度角和日照时间的不断变化, 光伏发电系统在不同季节可能产生不同的功率输出。在夏季, 由于受辐射时间更长和太阳高度角较高, 因此光伏功率通常相对较高。另外, 光伏系统本身的特性如组件类型、布局以及倾斜角度等也会对光伏功率的相关性产生影响。
3.4 多种预测模型对比分析
针对同一训练测试数据集, 分别采用支持向量机(Support Vector Regression, SVR)、决策树回归(Decision Tree Regressor, DTR)、K近邻(K-Nearest Neighbor, KNN)算法、LSTM、LightGBM和本文所提的KDE-Catboost模型进行光伏发电功率预测, 结果如表 2所示。
表 2
不同预测模型的预测误差和耗时
| 模型名称 | SRMSE | SMAE | SMSE | SR2 | 模型训练耗时/s |
| SVR | 0.29 | 0.25 | 0.54 | 0.89 | 58 |
| DTR | 0.23 | 0.20 | 0.48 | 0.88 | 41 |
| KNN | 0.25 | 0.16 | 0/50 | 0.92 | 33 |
| LSTM | 0.27 | 0.21 | 0.52 | 0.89 | 47 |
| LightGBM | 0.24 | 0.20 | 0.49 | 0.86 | 67 |
| Cat-Boost | 0.21 | 0.18 | 0.46 | 0.93 | 32 |
由表 2可以得出, 与其他5种模型相比, KDE-Catboost模型的SRMSE值分别下降了27.59%、8.69%、16.21%、23.33%、12.56%, 说明本文所提模型的预测精度更高, 适用于真实数据预测。另外, 本文所提模型的SR2值最高, 说明模型的拟合效果更好, 可靠性更高。
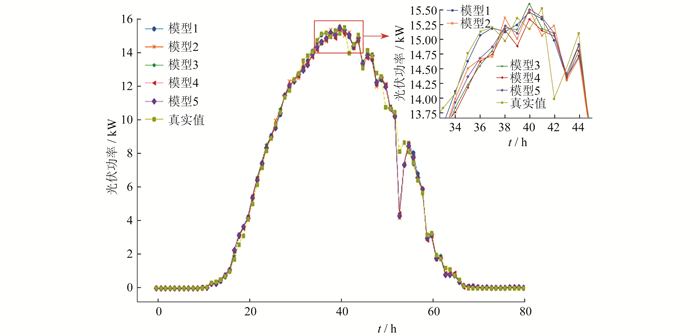
为验证所提模型的鲁棒性, 选取以下5种KDE-CatBoost模型: 模型1, 考虑近7 d光伏历史数据的KDE-CatBoost算法模型; 模型2, 考虑另外30 d光伏历史数据的KDE-CatBoost算法模型; 模型3, 考虑不同季节特性的KDE-CatBoost算法模型; 模型4, 在模型3基础上增加天气特征的KDE-CatBoost模型; 模型5, 考虑不同天气特征的KDE-CatBoost算法模型。5种模型的预测误差如表 3所示。5种模型的预测结果与真实值对比如图 2所示。
表 3
5种KDECatBoost模型的预测误差
| 模型名称 | SRMSE | SMAE | SMSE | SR2 |
| 1 | 0.21 | 0.18 | 0.46 | 0.93 |
| 2 | 0.22 | 0.20 | 0.47 | 0.92 |
| 3 | 0.23 | 0.17 | 0.48 | 0.91 |
| 4 | 0.20 | 0.18 | 0.45 | 0.91 |
| 5 | 0.23 | 0.19 | 0.48 | 0.90 |
根据表 3和图 2可知, 5种模型均具有较高的拟合度, 可见本文所提模型的鲁棒性较好。其原因是模型中KDE只需要设置带宽值一个参数, 使得算法结果相对稳定。另外, CatBoost算法在训练进程中对类别特征进行了分析处理, 并采用对称树作为基模型避免了过度拟合, 同时缩短了计算时长。
4 结论
本文提出KDE与CatBoost算法相结合的光伏功率超短期预测模型, 解决了预测模型普遍存在的超参数调优和过度拟合的难题, 模型具有更加广泛的适用性。具体结论如下。
(1) KDE与CatBoost算法相结合的光伏功率超短期预测模型与实际值具有较高的拟合精度, 且预测模型的鲁棒性较好。
(2) 算例结果表明, 所提模型的SRMSE相较于SVR、DTR、KNN、LSTM、LightGBM分别下降了27.59%、8.69%、16.21%、23.33%、12.56%。
参考文献
-
[1]DAS U K, TEY K S, SEYEDMAHMOUDIAN M, et al. Forecasting of photovoltaic power generation and model optimization: a review[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 912-928. DOI:10.1016/j.rser.2017.08.017
-
[2]WANG K J, QI X X, LIU H D. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network[J]. Applied Energy, 2019, 251: 113315. DOI:10.1016/j.apenergy.2019.113315
-
[3]DONG J, OLAMA M M, KURUGANTI T, et al. Novel stochastic methods to predict short-term solar radiation and photovoltaic power[J]. Renewable Energy, 2020, 145: 333-346. DOI:10.1016/j.renene.2019.05.073
-
[4]KORKMAZ D. SolarNet: a hybrid reliable model based on convolutional neural network and variational mode decomposition for hourly photovoltaic power forecasting[J]. Applied Energy, 2021, 300: 117410. DOI:10.1016/j.apenergy.2021.117410
-
[5]LI Q, ZHANG X Y, MA T J, et al. A multi-step ahead photovoltaic power prediction model based on similar day, enhanced colliding bodies optimization, variational mode decomposition, and deep extreme learning machine[J]. Energy, 2021, 224: 120094. DOI:10.1016/j.energy.2021.120094
-
[6]HEO J, SONG K, HAN S, et al. Multi-channel convolutional neural network for integration of meteorological and geographical features in solar power forecasting[J]. Applied Energy, 2021, 295: 117083. DOI:10.1016/j.apenergy.2021.117083
-
[7]DHINGRA B, TYAGI S, VERMA A, et al. A pseudo-labelled ensemble inference for fast and efficient real field photovoltaic system's power prediction[J]. Optik, 2023, 287: 171095. DOI:10.1016/j.ijleo.2023.171095
-
[8]MEI F, GU J Q, LU J X, et al. Day-ahead nonparametric probabilistic forecasting of photovoltaic power generation based on the LSTM-QRA ensemble model[J]. IEEE Access, 2020, 8: 166138-166149. DOI:10.1109/ACCESS.2020.3021581
-
[9]HE H, LU N Y, JIE Y J, et al. Probabilistic solar irradiance forecasting via a deep learning-based hybrid approach[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(11): 1604-1612. DOI:10.1002/tee.23231
-
[10]ZHANG Z L, LIU Z Y, CHEN T. Interval prediction of ultra-short-term photovoltaic power based on a hybrid model[J]. Electric Power Systems Research, 2023, 216: 109035. DOI:10.1016/j.epsr.2022.109035
-
[11]SANJARI M J, GOOI H B. Probabilistic forecast of PV power generation based on higher order Markov Chain[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2942-2952. DOI:10.1109/TPWRS.2016.2616902
-
[12]SUN T J, HU H Y, CAI R G, et al. Correlation analysis of drivers' natural driving behavior based on Kernel Density Estimation[J]. SAE International Journal of Sustainable Transportation Energy Environment & Policy, 2023, 4(2): 189-212.
-
[13]雷柯松, 吐松江·卡日, 伊力哈木·亚尔买买提, 等. 基于WGAN-GP和CNN-LSTM-Attention的短期光伏功率预测[J]. 电力系统保护与控制, 2023, 51(9): 108-118.