|
|
|
发布时间: 2023-12-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-10-15
中图法分类号: TP273.2
文献标识码: A
文章编号: 2096-8299(2023)06-0585-06
|
摘要
为了突破传统PID控制器在有机固废裂解系统中无法有效处理非线性系统、缺乏全局优化等局限性,提出了基于改进鱼鹰优化算法(OOA)的PID控制器。首先,对裂解釜温度系统传递函数模型的参数进行辨识;然后,运用改进OOA算法优化PID控制器参数;最后,通过MATLAB/Simulink进行仿真实验。仿真结果表明,改进后OOA-PID控制器相较传统的OOA-PID控制器控制效果提升显著,超调量减小了2.6%,系统动态响应时间缩短了约42%。
关键词
有机固废裂解釜; 鱼鹰优化算法; PID控制; 温度控制; 参数优化
Abstract
In order to break through the limitations of traditional PID controller in the thermal cracking system of organic solid waste, such as the inability to effectively deal with the nonlinear system and the lack of global optimisation, the PID controller with the improved Osprey Optimization Algorithm (OOA) is proposed.Firstly, the parameters of the transfer function model of the cracking kettle temperature system are identified by the step reaction two-point method; then, the improved OOA algorithm is applied to optimise the PID controller parameters.The simulation results by MATLAB/Simulink show that the control effect of the improved OOA-PID controller is significantly improved comparing with the traditional OOA-PID controller, the overshooting amount is reduced by 2.6%, and the dynamic response time of the system is shortened by about 42%.
Key words
organic solid waste cracking kettle; osprey optimization algorithm; PID control; temperature control; parameter optimization
PID控制器的有机固废热裂解釜温度控制PID控制是最常见和最基础的控制算法之一, 但对于有机固废热裂解这类复杂系统, PID控制器难以提供最佳的控制性能, 且控制器参数的调节较为繁琐。因此, 学者们提出使用智能优化算法优化PID参数。主要包括: 基于自然群集的元启发式算法, 如粒子群优化(Particle Swarm Optimization, PSO)算法[1-2]、蚁群优化(Ant Colony Optimization, ACO)算法[3]和人工蜂群(Artificial Bee Colony, ABC)算法[4-5]; 以动物狩猎和觅食获得食物为灵感的优化算法, 如鲸鱼优化算法(Whale Optimization Algorithm, WOA)[6]、白鲨优化器(White Shark Optimizer, WSO)[7]; 基于进化的元启发式算法, 如遗传算法(Genetic Algorithm, GA)[8-9]和差分进化(Differential Evolution, DE)算法[10]等。
鱼鹰优化算法(Osprey Optimization Algorithm, OOA)[11]是DEHGHANI M和TROJOVSKÝ P提出的一种新型生物元启发式优化算法, 模拟了鱼鹰在自然界中的狩猎捕食行为。基于对鱼鹰狩猎过程的模拟, 建立了鱼鹰勘探和开发两个阶段的数学模型。该算法具有全局搜索能力较强、收敛速度快、对初始值敏感性小等优点。
本文提出了一种改进OOA-PID控制器, 实现了对有机固废裂解釜温度的控制。其基本思路是利用鱼鹰找寻猎物的过程实现对PID参数的优化, 并通过MATLAB/Simulink与传统的PID、OOA-PID控制器、GA-PID控制器和PSO-PID控制器的控制效果进行仿真对比验证。
1 裂解釜温度模型建立
裂解釜温度控制系统由裂解釜、加热传输装置、温度测量变送环节构成。本文所研究的裂解釜主体由矩形外壳和旋转裂解釜两部分组成。在矩形外壳内壁, 加装隔热材料, 使得装置外壳与裂解釜之间形成加热室, 通过气体管道通入热空气, 并在管道入口安装气体流量阀, 控制加热喷嘴热流量, 实现对裂解釜的分段加热, 使裂解炉内形成一个不等温的梯度温度场。与此同时, 每两个隔板之间安装一个温度传感器, 可与气体流量阀相配合, 实现对温度的准确控制。
裂解釜内存在液相、气相和固相3种物质的流动, 使得裂解釜的流体力学特性变得非常复杂, 涉及很多物理变化和化学变化。裂解釜温度随着时间和空间的变化而发生变化, 因此建立精确的温度模型需要考虑多种因素的影响, 如热传导、热对流、热辐射等。在实际工程应用中, 为了便于分析, 将裂解釜简化为一阶滞后模型[12]。其传递函数为
| $ G(s)=\frac{K_{\mathrm{m}}}{T s+1} \mathrm{e}^{-\tau s} $ | (1) |
式中: G(s)——传递函数;
s——拉普拉斯算子;
Km——裂解釜中有机固废的转化效率;
T——时间常数;
e——欧拉常数;
τ——滞后时间。
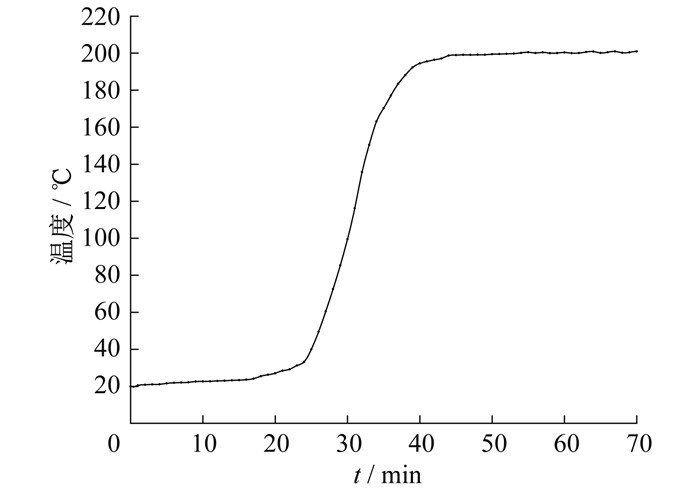
为得到上述模型的具体参数, 对裂解釜进行加热实验。设定裂解釜温度后, 每隔1 min对裂解釜温度值进行不间断记录, 直到裂解釜内温度保持在一定范围内, 绘制温度阶跃响应曲线, 具体如图 1所示。其中, 裂解釜的稳态值约为200 ℃。
根据采集到的温度实时数据, 可采用切线法、两点法、面积法、近似法等求取传递函数的系数。本文使用两点法求取传递函数[13], 一阶时滞系统的阶跃响应为
| $ Y(s)=G(s) U(s)=\frac{K_{\mathrm{m}} U}{s(T s+1)} \mathrm{e}^{-\tau s} $ | (2) |
式中: Y(s)——阶跃响应的拉氏变换;
U(s)——阶跃输入的拉氏变换;
U——阶跃信号的幅值。
对式(2)进行拉氏反变换得到
| $ \begin{aligned} & y(t)=L^{-1}[Y(s)]= \\ & L^{-1}\left[\frac{K_{\mathrm{m}} U}{s(T s+1)} \mathrm{e}^{-\tau s}\right]=K_{\mathrm{m}} U\left[1-\mathrm{e}^{\frac{-(t-\tau)}{T}}\right] \end{aligned} $ | (3) |
式中: y(t)——阶跃响应;
t——时间;
L——拉氏变换。
系统阶跃稳态响应的稳态值y(∞)
| $ y(\infty)=\lim _{t \rightarrow \infty} y(t)=K_{\mathrm{m}} U $ | (4) |
直接利用响应稳态值得到Km为
| $ K_{\mathrm{m}}=\frac{y(\infty)}{U} $ | (5) |
将阶跃响应曲线化为归一化曲线, 令
| $ y(t):=\frac{y(t)}{y(\infty)} $ | (6) |
一阶滞后系统的无因次阶跃响应为[13]
| $ y(t)=1-\mathrm{e}^{-\frac{(t-\tau)}{T}}, t \geqslant \tau $ | (7) |
当
| $ y\left(\frac{T}{2}+\tau\right)=1-\mathrm{e}^{-\frac{1}{2}} \approx 0.393 47 $ | (8) |
当t=T+τ时, 有
| $ y(T+\tau)=1-\mathrm{e}^{-1} \approx 0.632 12 $ | (9) |
采集阶跃响应曲线上的2个观测点数据[t1, y(t1)]和[t2, y(t2)], t2>t1>τ, 代入式(3)可得
| $ y\left(t_1\right)=K_{\mathrm{m}} U\left[1-\mathrm{e}^{\frac{-\left(t_1-\tau\right)}{T}}\right] $ | (10) |
| $ y\left(t_2\right)=K_{\mathrm{m}} U\left[1-\mathrm{e}^{\frac{-\left(t_2-\tau\right)}{T}}\right] $ | (11) |
由此可得
| $ \frac{t_1-\tau}{T}=-\ln \left[1-\frac{y\left(t_1\right)}{K_{\mathrm{m}} U}\right] $ | (12) |
| $ \frac{t_2-\tau}{T}=-\ln \left[1-\frac{y\left(t_2\right)}{K_{\mathrm{m}} U}\right] $ | (13) |
求解得
| $ T=\frac{t_2-t_1}{\ln \left[K_{\mathrm{m}} U-y\left(t_1\right)\right]-\ln \left[K_{\mathrm{m}} U-y\left(t_2\right)\right]} $ | (14) |
| $ \begin{aligned} & \tau= \\ & \frac{t_2 \ln \left[K_{\mathrm{m}} U-y\left(t_1\right)\right]-t_1 \ln \left[K_{\mathrm{m}} U-y\left(t_2\right)\right]-\left(t_2-t_1\right) \ln \left(K_{\mathrm{m}} U\right)}{\ln \left[K_{\mathrm{m}} U-y\left(t_1\right)\right]-\ln \left[K_{\mathrm{m}} U-y\left(t_2\right)\right]} \end{aligned} $ | (15) |
由式(14)、式(15)可知, 一阶时滞系统参数的精度与2个观测点[t1, y(t1)]、[t2, y(t2)]有关。因此, 可以在阶跃响应曲线上选择2个特殊的观测点, 如y(t1)=0.393 47、y(t2)=0.632 12, 则有
| $ \tau=2 t_1-t_2, T=2\left(t_2-t_1\right) $ | (16) |
由前文公式计算可得Km、T、τ的值, 最终得出一阶滞后传递函数为
| $ G(s)=\frac{4}{100 s+1} \mathrm{e}^{-20 s} $ | (17) |
2 基于改进OOA算法整定的PID控制器设计
2.1 传统PID控制器
PID控制器具有典型的结构和较高的灵活性, 原理简单、操作方便, 可根据被控对象的实际情况, 采用各种PID控制的变形和改进控制方式。在控制精度不高和控制速度要求不高的情况下, 选择传统PID控制易于取得较好的控制效果[14]。传统PID控制是一种基于比例、积分和微分3个部分的加权组合的控制算法, 其参数优化旨在寻找一组比例系数KP、积分系数KI和微分系数KD, 使系统的性能达到最优[15]。
PID控制器的控制规律可表示为
| $ u(t)=K_{\mathrm{P}} e(t)+K_{\mathrm{I}} \int_0^t e(t) \mathrm{d} t+K_{\mathrm{D}} \frac{\mathrm{d} e(t)}{\mathrm{d} t} $ | (18) |
| $ e(t)=y_{\mathrm{s}}(t)-r(t) $ | (19) |
式中: u(t)——PID控制器的输出;
e(t)——系统偏差;
ys(t)——系统输出;
r(t)——系统输入。
对式(18)进行拉氏变换, 表达成传递函数的形式为
| $ G(s)=\frac{U(s)}{E(s)}=K_{\mathrm{P}}+\frac{K_{\mathrm{I}}}{s}+K_{\mathrm{D}} s $ | (20) |
式中: E(s)——系统偏差的拉氏变换。
2.2 OOA算法的基本原理
2.2.1 群集初始化
初始化所有鱼鹰的位置。设鱼鹰位置种群矩阵为
| $ \boldsymbol{X}=\left[\begin{array}{c} \boldsymbol{X}_1 \\ \vdots \\ \boldsymbol{X}_i \\ \vdots \\ \boldsymbol{X}_N \end{array}\right]_{N \times 1}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & & \vdots & & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m} $ | (21) |
| $ x_{i, j}=b_{1, j}+r_{i, j}\left(b_{u, j}-b_{1, j}\right) $ | (22) |
式中: X——鱼鹰位置种群矩阵;
Xi——第i只鱼鹰的初始位置, i=1, 2, 3…, N;
N——鱼鹰数量;
xi, j——第j个问题变量中第i只鱼鹰的初始位置, j=1, 2, 3…, m;
m——问题变量个数;
ri, j——随机数, 取值范围为[0, 1];
bl, j、bu, j——第j个问题变量的下边界和上边界。
由于每只鱼鹰都是问题的候选解, 因此问题的目标函数值可以表示为
| $ \boldsymbol{F}=\left[\begin{array}{c} \boldsymbol{F}_1 \\ \vdots \\ \boldsymbol{F}_i \\ \vdots \\ \boldsymbol{F}_N \end{array}\right]_{N \times 1} $ | (23) |
式中: F——目标函数值;
Fi——Xi的目标函数值。
2.2.2 全局搜索
通过模拟鱼鹰的搜寻和观察过程, 寻找最优解。在鱼鹰确定鱼的位置后, 进行攻击捕食, 此时鱼鹰在搜索空间内的位置发生了显著变化。这一过程提高了OOA识别最优区域和避免陷入局部最优的探索能力。
鱼鹰搜索空间中目标函数值高的鱼鹰位置代表水下有鱼, 则第i只鱼鹰的鱼群位置为
| $ P_i=\left\{\boldsymbol{X}_k \mid k \in\{1,2,3 \cdots, N\} \cap \boldsymbol{F}_k<\boldsymbol{F}_i\right\} \cup\left\{\boldsymbol{X}_{\text {best }}\right\} $ | (24) |
式中: Pi——第i条鱼鹰的鱼群位置集合;
Xbest——Fi最优时对应的Xi值。
2.2.3 猎物定位
鱼鹰随机选择一条鱼的位置并攻击, 在模拟鱼鹰向鱼移动的基础上, 根据式(25)、式(26)确定鱼鹰的新位置
| $ x_{i, j}^1=x_{i, j}+r_{i, j}\left(P_{i, j}^{\mathrm{S}}-I_{i, j} \cdot x_{i, j}\right) $ | (25) |
| $ x_{i, j}^1=\left\{\begin{array}{l} x_{i, j}^1, b_{1, j} \leqslant x_{i, j}^1 \leqslant b_{\mathrm{u}, j} \\ b_{1, j}, x_{i, j}^1<b_{1, j} \\ b_{\mathrm{u}, j}, x_{i, j}^1>b_{\mathrm{u}, j} \end{array}\right. $ | (26) |
式中: xi, j1——第j个问题变量中第i只鱼鹰的新位置;
Pi, jS——第j个问题变量中第i只鱼鹰选择的鱼的位置;
Ii, j——集合{1, 2}中的随机数。
如果鱼鹰在新位置提高了目标函数的值, 则更新后鱼鹰的新位置为
| $ \boldsymbol{X}_i=\left\{\begin{array}{l} \boldsymbol{X}_i^1, \boldsymbol{F}_i^1<\boldsymbol{F}_i \\ \boldsymbol{X}_i, \boldsymbol{F}_i^1>\boldsymbol{F}_i \end{array}\right. $ | (27) |
式中: Xi1——第i只鱼鹰的新位置;
Fi1——Xi1的目标函数值。
2.3 改进OOA算法的原理
为了避免OOA算法陷入局部最优解, 提升算法局部搜索能力, 本文引入了鱼鹰进食算法。将鱼带到合适的位置, 在这一过程中鱼鹰的位置也产生了微小改变, 并向更优解收敛。对于OOA种群中的每一个成员, 随机生成一个“适合吃鱼的位置”为
| $ x_{i, j}^2=x_{i, j}+\frac{b_{1, i}+r_{i, j}\left(b_{u, j}-b_{1, j}\right)}{t_1} $ | (28) |
式中: xi, j2——第j个问题变量中第i只鱼鹰适合吃鱼的新位置;
t1——迭代次数, t1=1, 2, 3…, Tmax;
Tmax——算法的迭代总数。
其中,
| $ x_{i, j}^2=\left\{\begin{array}{l} x_{i, j}^2, b_{1, i} \leqslant x_{i, j}^2 \leqslant b_{\mathrm{u}, j} \\ b_{1, j}, x_{i, j}^2<b_{1, j} \\ b_{\mathrm{u}, j}, x_{i, j}^2>b_{\mathrm{u}, j} \end{array}\right. $ | (29) |
如果在这个新位置上目标函数的值有所改善, 则更新鱼鹰的位置为
| $ $ | (30) |
式中: Xi2——第i只鱼鹰适合吃鱼的新位置;
Fi2——Xi2的目标函数值。
OOA在猎物定位阶段通过更新所有鱼鹰的位置完成第一次迭代, 然后比较目标函数值的大小, 更新最佳候选值, 并进入下一次迭代。算法更新过程基于式(24)~式(30), 当满足终止条件时, 得到最优解。
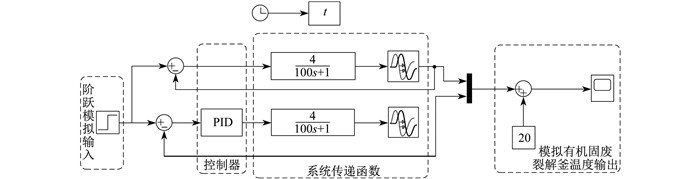
2.4 基于改进OOA-PID控制器的温度控制系统原理
2.5 改进OOA算法优化PID控制器参数流程
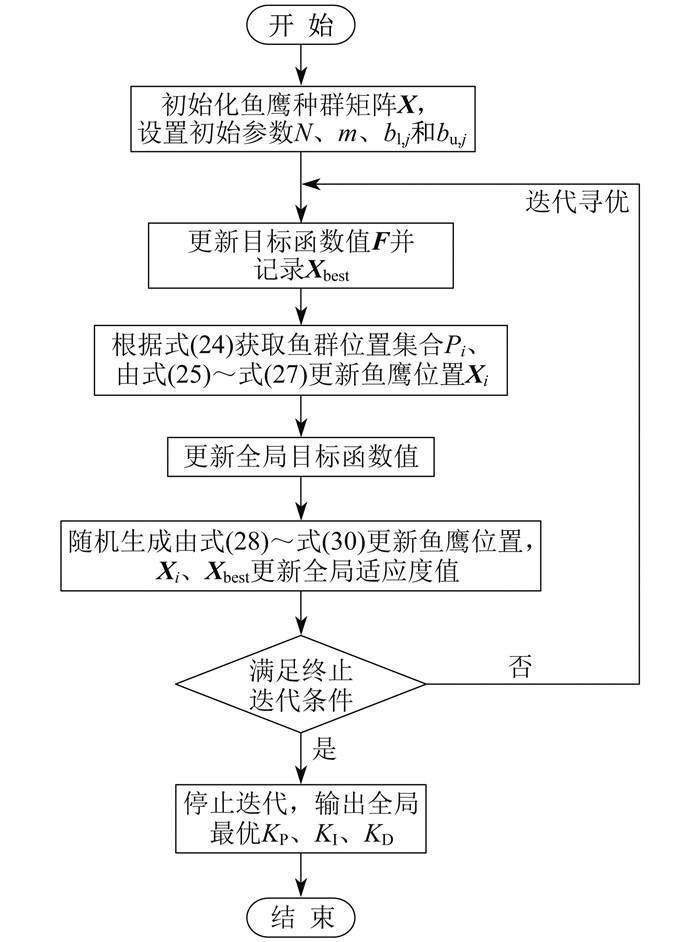
改进OOA算法优化PID控制器参数流程如图 3所示。
改进OOA算法优化PID控制器参数步骤如下[16]。
步骤1 初始化。在3维搜索空间中设置一组种群数为50的鱼鹰群来模拟KP、KI、KD的优化过程, 定义最大迭代次数500次, 鱼鹰运动的空间维数为3。根据式(21)、式(22)初始化鱼鹰群的初始位置, 并计算每只鱼鹰的目标函数值。
步骤2 全局迭代搜索。通过比较每只鱼鹰的目标函数值, 更新鱼鹰的最优位置和鱼鹰群的最优位置, 搜索出一组全局最优解。
步骤3 更新邻近区域。随机定义最优位置, 通过判断每只鱼鹰的目标函数值是否升高来更新鱼鹰个体的位置, 获得当前迭代中的最优解。
步骤4 达到终止条件。当迭代次数达到最大迭代次数或目标函数值达到最大目标函数阈值时停止程序, 输出当前迭代的最优解作为PID控制器的3个参数, 否则返回步骤2继续迭代。
3 仿真结果与分析
3.1 传统PID控制器仿真
3.2 改进OOA算法优化的PID控制器仿真
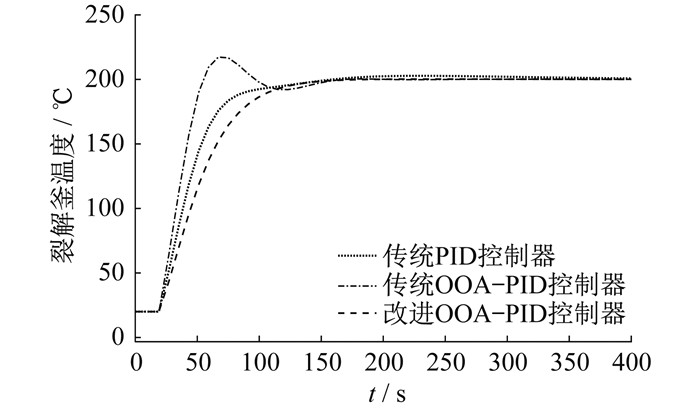
考虑到智能算法的随机性, 多次重复调用程序与仿真, 得到3种控制器的Simulink仿真结果如图 5所示。
采用不同控制器的系统阶跃响应性能指标如表 1所示。
表 1
采用不同控制器的系统阶跃响应性能指标
| 控制器 | 峰值时间/s | 上升时间/s | 超调量/% | 响应时间/s |
| 传统PID | 218.5 | 89.62 | 9.2 | 73.4 |
| 传统OOA-PID | 95.3 | 69.46 | 2.6 | 85.5 |
| 改进OOA-PID | 73.8 | 49.03 | 0 | 62.1 |
根据图 5和表 1数据可知, 改进后的OOA-PID控制器较传统OOA-PID控制器呈现出了显著的优越性, 超调量减少了2.6%, 控制系统的动态响应时间缩短了约42%。相较于传统PID控制器, 超调量减少了9.2%, 系统的响应时间缩短了约66%。
4 结论
为将裂解釜内温度控制在安全的范围内, 从而实现有机固废裂解系统的节能降耗、降低设施运营成本。本文对裂解釜温度控制传递函数模型参数进行辨识, 通过改进OOA算法对PID控制器参数进行了优化设计。通过仿真试验与传统PID控制器、传统OOA-PID控制器控制效果进行对比分析, 得出该方法的优点如下。
(1) PID控制器参数整定方便, 但传统PID控制器依靠工程经验和系统输出多次调整参数, 难以获取最佳参数值, 其控制效果不能满足生产要求。基于OOA算法能实现对PID参数的自行整定, 减小了系统的超调量, 大大缩短了系统的动态响应时间。
(2) 相较于OOA算法, 改进OOA算法有更快的响应速度, 全局搜索和局部搜索能力更强, 有效避免了陷入局部最优解的问题。
(3) 改进OOA算法的PID控制器在应对干扰时响应速度快, 无超调, 具有较高的鲁棒性, 且动态特性良好、没有稳态误差。因此, 在实际应用中, 可以结合改进OOA算法对裂解釜温度控制系统的PID参数进行优化, 提高裂解釜温度控制系统的控制性能和稳定性。本文的研究结果可为工业应用设计出更高效、更可靠的裂解系统。
参考文献
-
[1]XIANG Z L, JI D M, ZHANG H, et al. A simple PID-based strategy for particle swarm optimization algorithm[J]. Information Sciences, 2019(6): 558-574.
-
[2]JAINN K, NANGIA U, JAIN J. A review of particle swarm optimization[J]. Journal of the Institution of Engineers (India): Series B, 2018, 99(4): 407-411. DOI:10.1007/s40031-018-0323-y
-
[3]DENG W, XU J J, SONG Y J, et al. An effective improved co-evolution ant colony optimisation algorithm with multi-strategies and its application[J]. International Journal of Bio-Inspired Computation, 2020, 16(3): 158-170. DOI:10.1504/IJBIC.2020.111267
-
[4]李艳生, 万勇, 张毅, 等. 基于人工蜂群-自适应遗传算法的仓储机器人路径规划[J]. 仪器仪表学报, 2022, 43(4): 282-290.
-
[5]WANG Y, YOU J, HANG J Q, et al. An improved artificial bee colony (ABC) algorithm with advanced search ability[C]//Proceedings of the 8th International Conference on Electronics Information and Emergency Communication. Beijing: IEEE, 2018: 91-94.
-
[6]MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016(5): 51-67.
-
[7]BRAIK M, HAMMOURI A, ATWAN J, et al. White Shark Optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems[J]. Knowledge-Based Systems, 2022, 243: 108457. DOI:10.1016/j.knosys.2022.108457
-
[8]BILAL, PANT M, ZAHEER H, et al. Differential evolution: a review of more than two decades of research[J]. Engineering Applications of Artificial Intelligence, 2020(4): 103479.
-
[9]DING Y M, ZHANG W L, YU L, et al. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis[J]. Energy, 2019(4): 582-588.
-
[10]AHMAD M F, ISA N A M, LIM W H, et al. Differential evolution: a recent review based on state-of-the-art works[J]. Alexandria Engineering Journal, 2022, 61(5): 3831-3872. DOI:10.1016/j.aej.2021.09.013
-
[11]DEHGHANI M, TROJOVSKÝ P. Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J]. Frontiers in Mechanical Engineering, 2023, 8: 1126450. DOI:10.3389/fmech.2022.1126450
-
[12]宣铁锋, 张军. 基于专家PID的电阻炉温度控制策略[J]. 仪表技术, 2020(2): 30-33.
-
[13]丁锋, 徐玲, 刘喜梅. 传递函数辨识(1): 阶跃响应两点法和三点法[J]. 青岛科技大学学报(自然科学版), 2018, 39(1): 1-14.
-
[14]刘金琨. 先进PID控制MATLAB仿真[M]. 4版. 北京: 电子工业出版社, 2016: 220-224.
-
[15]任宇希, 丁振伟, 莫愁, 等. 基于秃鹰算法的PID参数自整定[J]. 电气传动自动化, 2022, 44(3): 6-8.
-
[16]李小魁, 黄全振, 黄明明. 基于蜻蜓算法的PID控制器参数优化[J]. 现代电子技术, 2018, 41(12): 102-107.
-
[17]杨旭红, 陈阳, 方剑峰, 等. 基于改进PSO-PID控制器的核电站汽轮机转速控制[J]. 控制工程, 2022, 29(12): 2177-2183.