|
|
|
发布时间: 2023-12-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-05-09
中图法分类号: TM914
文献标识码: A
文章编号: 2096-8299(2023)06-0578-07
|
摘要
光伏阵列受部分遮阴影响,其功率-电压特性曲线呈多峰状,导致传统最大功率点跟踪(MPPT)算法失效,因此提出了一种改进的非洲秃鹫优化算法(AVOA)运用于光伏的MPPT控制。首先,引入Tent混沌映射使种群位置更具多样性,避免过早收敛。然后,优化算法在探索和开发阶段的更新策略,减少计算力的浪费,提高寻优速率。最后,在MATLAB 2022b/Simulink环境下,应用所提算法对不同辐照情况的3组工况进行仿真。实验结果表明,在多峰MPPT控制中,该算法具有寻优效率高、收敛速度快等特点,能有效地提升复杂遮阴环境下光伏能源的利用率。
关键词
光伏发电; 非洲秃鹫优化算法; 最大功率点跟踪; 部分遮阴
Abstract
Under the influence of partial shading, the power and voltage characteristic curve of PV array presents a multi-peak shape, which leads to the failure of traditional MPPT algorithm.Thus an improved African vultures optimization algorithm (AVOA)is proposed for MPPT photovoltaic control.Firstly, Tent chaotic mapping is introduced to make the population position more diverse and avoid premature convergence.Then, the update strategy of the algorithm is optimized in the exploration and development stage to reduce the waste of computing power and improve the search rate.Finally, in the MATLAB2022b/Simulink environment, the proposed algorithm is used to simulate three groups of conditions under different irradiation conditions.The results show that the algorithm has the characteristics of high optimization efficiency and fast convergence rate in the multi-peak MPPT control, which can effectively improve the utilization rate of photovoltaic energy in the complex shading environment.
Key words
photovoltaic power generation; african vulture optimization algorithm; maximum power point tracking; partial shading
全球经济的飞速发展, 伴随着能源的巨额消耗。为解决化石能源带来的高碳排放问题, 可再生能源被各国积极研究开发, 其中光伏能源作为取之不尽、用之不竭、无污染、无噪声的绿色清洁能源之一受到国内外极大的关注[1]。当光伏系统实际投运后, 在辐照强度不均匀情况下光伏阵列的功率-电压特性曲线呈多峰状, 致使电导增量法[2]、扰动观察法[3]等传统控制算法无法搜索到全局最优解。
文献[4]将灰狼算法(Gray Wolf Optimization, GWO)与传统扰动观察法相结合, 保证了系统寻优速率, 但搜寻过程振荡频率较高。文献[5]提出一种蝙蝠与粒子群(Particle Swarm Optimization, PSO)混合算法, 有效地提高跟踪速率, 但没有考虑动态跟踪的成功率, 且对算法参数设置要求高。文献[6]提出一种双层结构的GWO算法, 上层在GWO算法中嵌入Levy飞行与多项式变异策略, 下层采用扰动观察法进行局部跟踪, 既能快速寻优, 又能避免动态过程中的功率振荡。文献[7]在鲸鱼优化算法的基础上引入混沌映射与非线性收敛因子, 在寻优速度、精度等方面均有显著的效果。
本文以非洲秃鹫优化算法(African Vulture Optimization Algorithm, AVOA)为研究对象, 在原始算法的基础上提出了一种改进的AVOA算法。其通过在算法的初始化中引入混沌映射增加种群多样性; 优化算法在探索和开发阶段更新策略, 减小跟踪过程的振荡幅度以及控制的复杂程度, 从而使算法更适配光伏最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制。在软件MATLAB 2022b/Simulink上, 分别对PSO、GWO以及改进的AVOA在不同工况下进行仿真对比, 验证本文所提算法在解决MPPT上性能更优越。
1 光伏电池等效电路和电池阵列输出特性
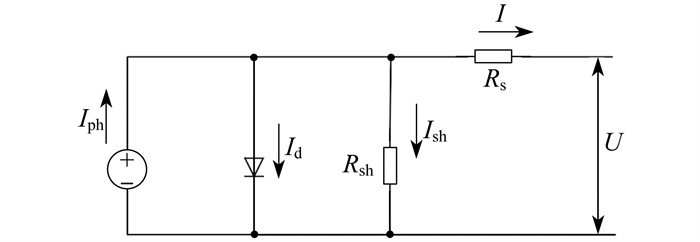
为模拟光伏电池的运作方式, 将其简化成1个由直流电源、二极管、串并联电阻组成的等效电路, 如图 1所示。
由图 1可得, 单个光伏电池的伏安特性为
| $ I=I_{\mathrm{ph}}-I_{\mathrm{d}}-I_{\mathrm{sh}} $ | (1) |
| $ I_{\mathrm{d}}=I_{\mathrm{o}}\left(\mathrm{e}^{\frac{q}{A K T}\left(U+I R_{\mathrm{s}}\right)}-1\right) $ | (2) |
| $ I_{\mathrm{sh}}=\frac{U+I R_{\mathrm{s}}}{R_{\mathrm{sh}}} $ | (3) |
式中: I——光伏电池的输出电流, A;
Iph——光能在光伏电池中激发的电流, A;
Id——暗电流, A;
Ish——旁路电流, A;
q——电子电荷, 取1.602×10-19 C;
A——理想因子;
K——玻尔兹曼常数, 取1.381×10-23 J/K;
T——绝对温度, K;
Rs——串联电阻, Ω;
U——光伏电池的输出电压, V;
Rsh——并联电阻, Ω。
因为单个光伏电池输出的电能过小, 无法正常供应日常生活中的电气设备, 所以通过将多个光伏电池进行串并联形成光伏阵列, 串联操作须保证各个太阳能电池片输出相同的电流。但处于阴影下的电池片输出的电流小于线路上的电流, 反而消耗系统的能量, 造成部分电池片过热甚至烧毁。这种现象被称为热斑现象[8]。通过在每个光伏电池的两端反向并联1个二极管来阻止热斑现象的发生, 但旁路二极管的并入导致了功率-电压曲线出现多峰状。
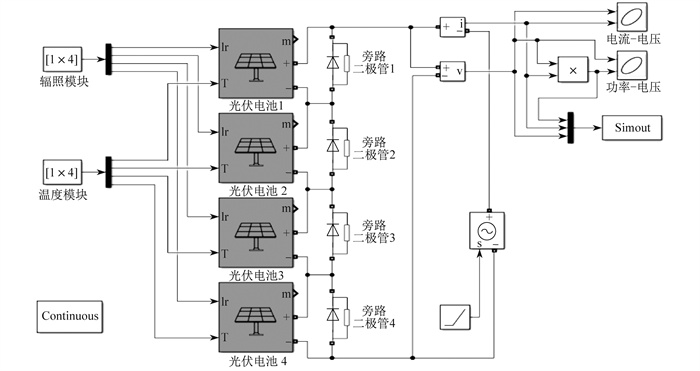
在MATLAB 2022b/Simulink平台上建立4×1串联式的光伏阵列如图 2所示。该组件开路电压Uoc为50.93 V, 峰值电压Ump为42.8 V, 短路电流Isc为6.2 V, 峰值电流Imp为5.84 V。
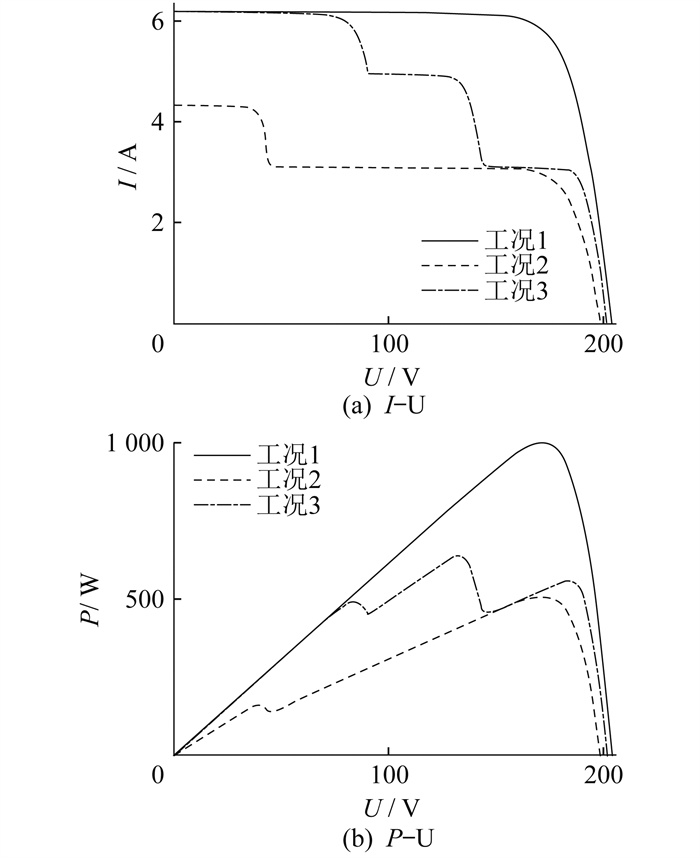
设置3种不同的光照分布的工况, 如表 1所示。3种工况下, 光伏阵列的电流-电压(I-U)输出曲线和功率-电压(P-U)输出曲线如图 3所示。
表 1
3种工况下的光照强度和全局最大功率点
| 工况 | 光照强度/(W·m-2) | 全局最大功率/W |
| 1 | 1 000、1 000、1 000、1 000 | 1 000.0 |
| 2 | 500、700、500、500 | 508.6 |
| 3 | 1 000、1 000、500、800 | 639.3 |
由图 3可知, 光伏组件在均匀的光照强度下, 功率输出曲线只有一个波峰, 即最大点, 而在不均匀的光照强度下, 光伏组件输出的功率波形图均出现了多个波峰, 但最大值有且仅有一个。本文设置的3种工况分别对应着单波峰、双波峰、三波峰, 由此可以考查各个控制算法的性能。
2 算法介绍
2.1 AVOA算法
AVOA算法是于2021年提出的元启发式算法, 主要通过模拟非洲秃鹫特有的觅食行为进行寻优。AVOA算法首先假定在解空间内存在N只秃鹫, 根据适应度大小分出最优、次优2只秃鹫, 剩余的秃鹫围绕前2只秃鹫进行觅食[9]。
AVOA算法迭代步骤如下[10]。
步骤1 选出种群中最佳的秃鹫。构建初始种群后, 对所有解的适应度进行计算, 选出最优解作为第1组最佳秃鹫, 次优解作为第2组最佳秃鹫, 其他秃鹫通过式(3)向第1组和第2组的位置移动, 每次迭代后, 整个种群重新计算适应度。
| $ \boldsymbol{R}(i)=\left\{\begin{array}{l} \boldsymbol{B}_{\text {estVulture }_1}(i), p=L_1 \\ \boldsymbol{B}_{\text {estVulture }_2}(i), p=L_2 \end{array}\right. $ | (4) |
| $ p=\frac{f_n}{\sum\limits_{n=1}^m f_n} $ | (5) |
式中:R(i)——最佳秃鹫的矢量位置;
i——当前迭代次数;
BestVulture1(i)、BestVulture2(i)——最优、次优秃鹫位置;
p——选择最佳解的概率;
L1、L2——搜寻前给定的参数, 介于0到1之间, 且L1+L2=1;
fn——每个秃鹫个体的自适应度值;
m——第1组秃鹫和第2组秃鹫的数量。
步骤2 计算秃鹫的饥饿率。秃鹫若是感到饱腹, 个体蕴含的能量高, 会前往更远的位置觅食。若是感到饥饿, 便无法远距离移动, 会选择在更强壮的秃鹫旁觅食。利用式(6)、式(7)对这种行为进行数学建模。
| $ t=h\left[\sin ^W\left(\frac{\pi i}{2 I}\right)+\cos \left(\frac{\pi i}{2 I}\right)-1\right] $ | (6) |
| $ F=\left(2 r_{\text {and }_1}+1\right) \cdot z \cdot\left(1-\frac{i}{I}\right)+t $ | (7) |
式中: t——防止陷入局部最优解的调节参数;
h——-2~2之间的随机数;
W——优化作业前设置的固定数值参数;
I——最大迭代次数;
F——秃鹫的饥饿率;
rand1——0~1之间的随机数;
z——在-1~1之间的随机数, 每次迭代都会发生变换。
当|F|大于1时, 秃鹫就会在不同的地方觅食, 算法进入探索阶段; 如果|F|小于1时, 算法进入开发阶段, 秃鹫在附近觅食。
步骤3 进入探索阶段。这一阶段算法模拟秃鹫觅食的行为规律, 秃鹫在不同的随机区域觅食, 具备两种不同的策略, 通过用户定义的参数P1来判断采取何种探索策略。P1取值在0到1之间, 该过程如式(8)所示。
| $ \begin{aligned} & \boldsymbol{P}(i+1)= \\ & \left\{\begin{array}{l} \boldsymbol{R}(i)-|\boldsymbol{X} \cdot \boldsymbol{R}(i)-\boldsymbol{P}(i)| \cdot F, P_1 \geqslant r_{\mathrm{and}_{\mathrm{P}}} \\ \boldsymbol{R}(i)-F+r_{\mathrm{and}_2}\left[\left(\boldsymbol{u}_{\mathrm{b}}-\boldsymbol{l}_{\mathrm{b}}\right) r_{\mathrm{and}_3}+\boldsymbol{l}_{\mathrm{b}}\right], \text { 其他 } \end{array}\right. \end{aligned} $ | (8) |
式中:P(i)、P(i+1)——秃鹫当前和下一次矢量位置;
X——秃鹫随机移动的地方, 被用作增加随机的系数向量;
randP1、rand2、rand3——0~1之间的随机数;
lb、ub——寻优边界的上下限。
步骤4 进入开发阶段。当|F|的值处于0.5与1之间, 算法进入开发阶段的第一阶段。在这一阶段, 算法采用2种截然不同的旋转飞行和围攻策略, 制定参数P2来确定策略的选择。该过程的公式为
| $ \begin{aligned} & \boldsymbol{P}(i+1)= \\ & \left\{\begin{array}{l} |\boldsymbol{X} \cdot \boldsymbol{R}(i)-\boldsymbol{P}(i)| \cdot\left(F+r_{\mathrm{and}_4}\right)- \\ \;\;\;\;\boldsymbol{R}(i)+\boldsymbol{P}(i), P_2 \geqslant r_{\mathrm{and}_{\mathrm{P} 2}}\\ \boldsymbol{R}(i)-\left(\boldsymbol{S}_1+\boldsymbol{S}_2\right), \text { 其他 } \end{array}\right. \end{aligned} $ | (9) |
其中,
| $ \begin{aligned} & \boldsymbol{S}_1=\boldsymbol{R}(i) \cdot \frac{r_{\text {and }_5} \cdot \boldsymbol{P}(i)}{2 \pi} \cdot \cos (\boldsymbol{P}(i)) \\ & \boldsymbol{S}_2=\boldsymbol{R}(i) \cdot \frac{r_{\text {and }_5} \cdot \boldsymbol{P}(i)}{2 \pi} \cdot \sin (\boldsymbol{P}(i)) \end{aligned} $ | (10) |
式中: rand4、randP2、rand5——0~1之间的随机数。
步骤5 当|F|的值小于0.5时, 算法进入开发阶段的第二阶段。此时所有类型的饥饿秃鹫都会逐渐向领头秃鹫附近的食物源聚集靠拢, 并开展了夺食的侵略斗争, 由参数P3决定采取的策略, 该过程如式(11)所示。
| $ \begin{aligned} & \boldsymbol{P}(i+1)= \\ & \left\{\begin{array}{l} \frac{\boldsymbol{A}_1+\boldsymbol{A}_2}{2}, P_3 \geqslant r_{\text {and }_3} \\ \boldsymbol{R}(i)-|\boldsymbol{R}(i)-\boldsymbol{P}(i)| \cdot F \cdot \operatorname{Levy}(d), \text { 其他 } \end{array}\right. \end{aligned} $ | (11) |
其中,
| $ \begin{aligned} \boldsymbol{A}_1 & =\boldsymbol{B}_{\text {estVulture }_1}(i)-\frac{\boldsymbol{B}_{\text {estVulture }_1}(i) \cdot \boldsymbol{P}(i)}{\boldsymbol{B}_{\text {estVulture }_1}(i)-\boldsymbol{P}(i)^2} \cdot F, \\ \boldsymbol{A}_2 & =\boldsymbol{B}_{\text {estVulture }_2}(i)-\frac{\boldsymbol{B}_{\text {estVulture }_2}(i) \cdot \boldsymbol{P}(i)}{\boldsymbol{B}_{\text {estVulture }_2}(i)-\boldsymbol{P}(i)^2} \cdot F \end{aligned} $ | (12) |
式中: randP3——0~1之间的随机数;
Levy(d)——Levyflight(LF)函数。
2.2 混沌优化理论
执行AVOA算法前, 随机生成种群位置分布于解空间各处。该过程存在较大的随机性及不稳定性, 如果初始位置不利, 在不断迭代计算中, 算法会因缺少早期探索, 提前收敛, 陷入局部最优。本文引用的混沌优化具有较好的遍历性[11], 与AVOA算法相结合, 可以确保秃鹫初始种群的多样性, 提高全局搜索的能力。采用使用率较高的Logistic映射作为混沌映射模型, 模型如下
| $ X_{n+1}=\mu X_n\left(1-X_n\right) $ | (13) |
式中: Xn、Xn+1——混沌映射前后的种群个体, 取值范围在0~1;
μ——控制变量, 取值范围在0~4。
2.3 改进AVOA算法
与解决其他问题不同, MPPT控制在搜索后期需要稳态过程, 以确保输出的最大功率曲线平稳, 但AVOA算法在探索和开发阶段策略选择机制复杂, 更新公式多, 使得AVOA算法搜索过程持续振荡, 难以实现最大功率的平稳输出。因此, 本文对此阶段的AVOA算法进行优化更新。
探索阶段取消以随机值选择更新策略的机制, 并将式(7)中的随机系数向量X优化为单位向量。具体公式如下:
| $ \boldsymbol{P}(i+1)=\boldsymbol{R}(i)-|\boldsymbol{R}(i)-\boldsymbol{P}(i)| \cdot F, F \geqslant 1 $ | (14) |
开发阶段只保留第二阶段, 同样取消随机选择策略机制。具体公式如下:
| $ \begin{gathered} \boldsymbol{P}(i+1)=\boldsymbol{R}(i)-|\boldsymbol{R}(i)-\boldsymbol{P}(i)| \cdot F \cdot \operatorname{Levy}(d), \\ F<1 \end{gathered} $ | (15) |
3 改进AVOA算法在MPPT中的应用
在光伏技术里, MPPT控制一般是通过DC/DC电路的占空比实现的, 光伏电池组输出的直流电压电流作为输入量, 输出量为占空比。仿真运行后, MPPT控制模块执行改进AVOA算法, 其中秃鹫个体代表占空比, 搜索到最优的占空比并输入给脉冲宽度调制以驱动DC/DC电路改变电路中的输入电阻, 从而控制光伏阵列输出最大功率[12]。另外, MPPT控制还需要设置终止判定策略以及重启条件。
3.1 终止判定策略
为了减小输出功率波动, 使用改进AVOA算法寻优, 为了后期能及时停止算法的迭代, 应给改进AVOA算法添加终止条件。将秃鹫的位置视为MPPT控制输出的占空比, 设置当最优个体与最差个体的位置差小于一个非常小的阈值S时, 认为算法已搜索到最大功率点, 停止迭代。S的值越小, 精度也越高。
3.2 重启条件
当出现意外遮挡物导致光照情况发生变化时, 光伏系统的输出功率也相应地发生变化。为减少功率损失, 需重启MPPT。重启策略为
| $ \left|\frac{P_k-P_{k-1}}{P_k}\right| \geqslant 0.05 $ | (16) |
式中: Pk、Pk-1——当前与上个周期的功率。
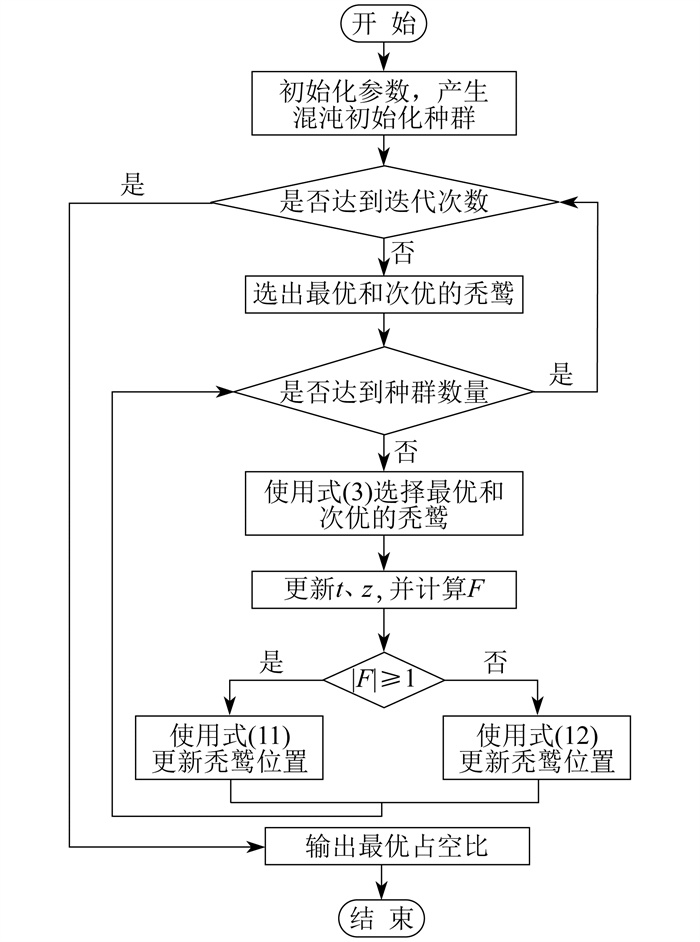
3.3 算法流程
整体算法流程如图 4所示。
4 仿真实验及结果分析
4.1 仿真系统搭建
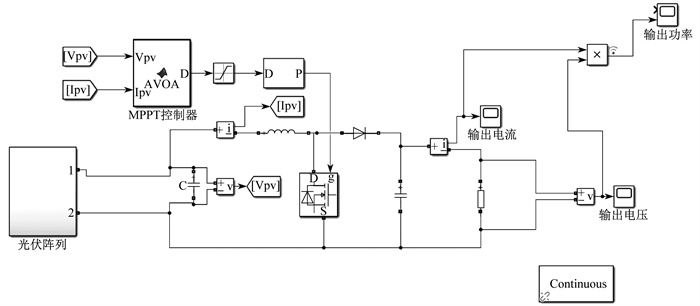
在MATLAB 2022b/Simulink仿真平台搭建一个由光伏阵列、MPPT控制器、Boost升压电路和负载构成的光伏仿真系统, 如图 5所示。为简化实验, 将此系统的负载设置为阻性负载。
为验证本文采用的改进AVOA算法在实现MPPT上的有效性, 分别对PSO、GWO、改进AVOA算法在局部阴影下的MPPT系统中进行仿真, 分析三者寻优效率、收敛速度。为实现公平对比, 3种算法的种群大小均为5, 最大迭代次数设置为20, 种群初始化的随机值设置在[0, 1], 终止条件S设置为0.02。
4.2 静态遮阴下的MPPT仿真
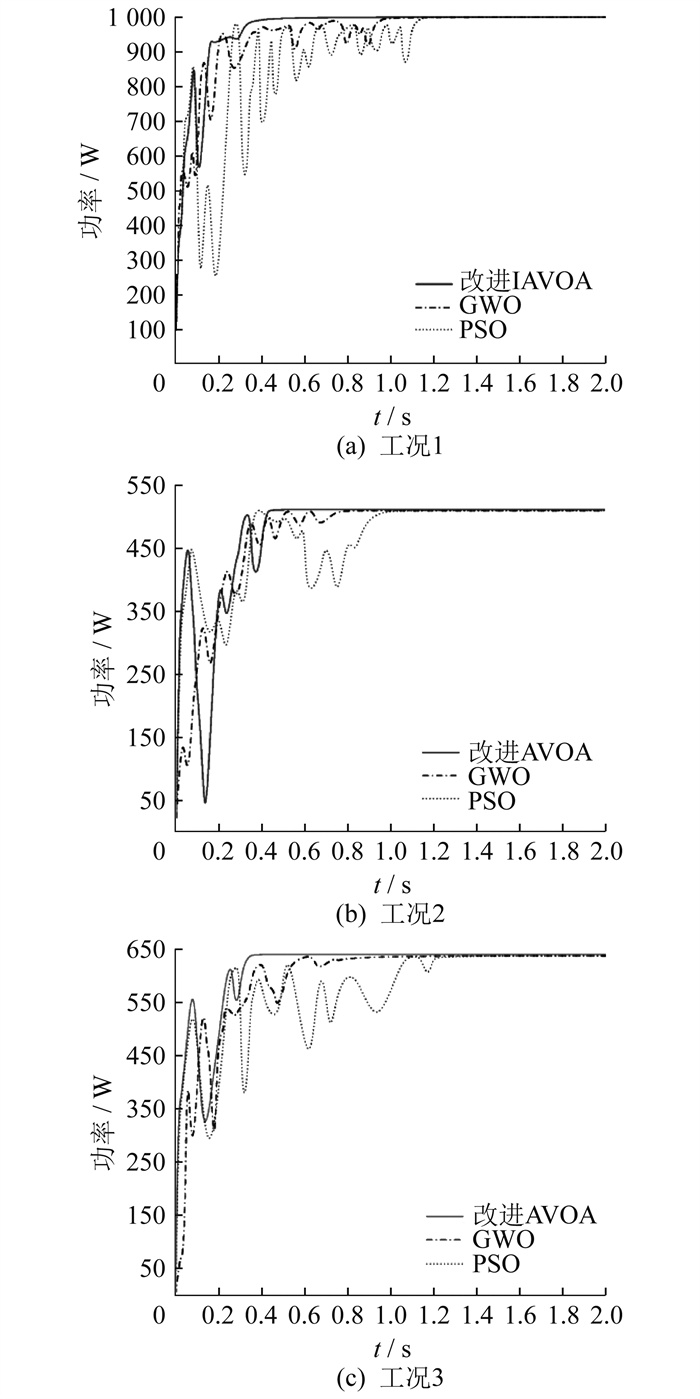
为了验证在静态遮阴下本文采用的改进AVOA算法的MPPT性能, 使用图 5的仿真模型, 仿真温度设置为25 ℃, 运行时长为2 s, 对表 1中的工况1、2、3进行仿真, 结果如图 6所示。
3种算法运行结果对比如表 2所示。由表 2可知, 改进AVOA在MPPT控制上的平均收敛时间在0.40 s, 追踪效率更是稳定在99.9%, 相比PSO、GWO算法, 改进AVOA算法兼顾了快速性和精确性, 且整个搜索过程振荡较小, 大大提高了光伏能源的利用率, 非常适合工作在辐照强度不均匀的状态下。
表 2
3种算法运行结果对比
| 工况 | 实际最大功率/W | MPPT控制方法 | 追踪到的最大功率/W | 收敛时间/s | 追踪效率/% |
| 1 | 1 000.0 | 改进AVOA | 999.5 | 0.44 | 99.9 |
| GWO | 999.3 | 0.97 | 99.9 | ||
| PSO | 997.2 | 1.18 | 97.2 | ||
| 2 | 508.6 | 改进AVOA | 508.3 | 0.43 | 99.9 |
| GWO | 508.1 | 0.74 | 99.8 | ||
| PSO | 506.9 | 1.12 | 99.6 | ||
| 3 | 639.3 | 改进AVOA | 639.1 | 0.34 | 99.9 |
| GWO | 638.1 | 0.78 | 99.8 | ||
| PSO | 637.4 | 1.21 | 99.7 |
4.3 动态遮阴下的MPPT仿真
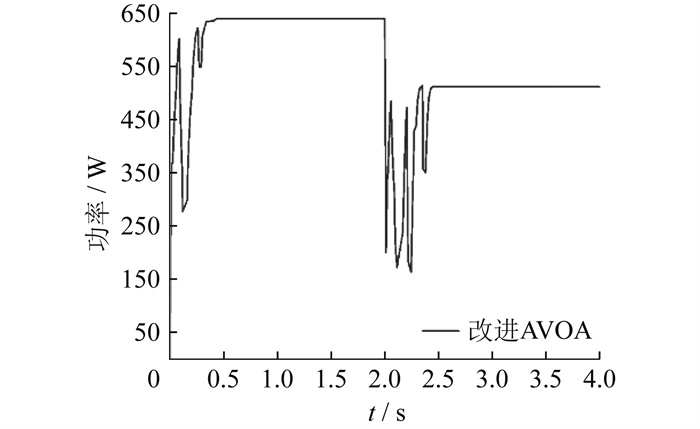
为了验证在动态遮阴下, 本文采用的改进AVOA算法的MPPT性能, 设置仿真时长4 s。在仿真时长达到2 s时, 模型中的4块串联光伏电池的光照强度由1 000 W/m2、1 000 W/m2、500 W/m2、800 W/m2变为500 W/m2、700 W/m2、500 W/m2、500 W/m2, 即从工况3变到工况2, 仿真结果如图 7所示。辐照条件在2 s发生突变, 由表 1可知, 最大功率值理想值由639.3 W下跌至508.6 W。由图 7可知, 改进AVOA算法在2.43 s搜寻到了最大功率值508.3 W并趋于平稳, 与理想值仅差0.3 W。这表明时变的情况下该算法也能实现最大功率点的追踪, 且具有良好的追踪效率以及较快的收敛速度。
5 结语
本文为解决光伏系统中的MPPT问题, 提出了改进AVOA算法的控制方案。实验结果表明, 改进AVOA算法在MPPT控制上切实可行, 既大大减少了算法的复杂程度, 又增强了避免陷入局部最优的能力, 保证了搜索的成功率。通过仿真对比发现, 改进AVOA在收敛速度和搜索精度上都高于PSO、GWO算法, 且在动态变化的光照条件下也能够实现高效的功率追踪, 极大地提升了光伏能源的利用率, 具有较高的实用价值。
由于条件有限, 本文光伏系统设计仅是软件仿真, 尚未在实际应用中得到验证, 所以下一步需要进行光伏系统的硬件设计和实验验证。
参考文献
-
[1]周昰彤, 鞠振河. 关于太阳能发电技术的综述及展望[J]. 电子世界, 2020(1): 83-84.
-
[2]刘明亮, 张逸, 范元亮, 等. 一种基于变步长电导增量法的自适应MPPT控制策略[J]. 可再生能源, 2017, 35(5): 681-688. DOI:10.3969/j.issn.1671-5292.2017.05.008
-
[3]王硕禾, 郑俊观, 张国驹, 等. 基于改进型变步长扰动观察法的光伏系统MPPT研究[J]. 广西大学学报(自然科学版), 2018, 43(3): 1032-1043.
-
[4]沈磊, 徐岸非, 黄晴宇, 等. 基于GWO-PSO算法的局部阴影光伏MPPT研究[J]. 湖北工业大学学报, 2022, 37(2): 25-29.
-
[5]黄荣赓, 陈路遥. 基于蝙蝠与粒子群混合优化算法的光伏MPPT研究[J]. 电源技术, 2022, 46(3): 324-328.
-
[6]付文龙, 孟嘉鑫, 张赟宁, 等. 复杂遮荫下基于改进GWO的光伏多峰MPPT控制[J]. 太阳能学报, 2023, 44(3): 435-442.
-
[7]陈斌, 王俊江, 赵明胤, 等. 基于改进鲸鱼优化算法的光伏发电系统MPPT控制研究[J]. 电力系统及其自动化学报, 2023, 35(2): 19-26.
-
[8]王利峥, 刘光宇. 基于简化蚁群算法的光伏MPPT跟踪控制[J]. 电源技术, 2020, 44(8): 1152-1155.
-
[9]ABDOLLAHZADEH B, GHAREHCHOPOGH F S, MIRJALILI S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems[J]. Computers & Industrial Engineering, 2021, 158: 107408.
-
[10]王忠义, 崔东文. 基于小波包分解-非洲秃鹫优化算法-深度极限学习机的水文预报模型及其应用[J]. 水电能源科学, 2022, 40(8): 26-31.
-
[11]李大华, 聂前, 田禾, 等. 改进海鸥优化算法在光伏系统MPPT中的应用[J]. 电源技术, 2022, 46(5): 556-559.
-
[12]杨永康, 缪书唯. 基于DE-GWO算法的光伏系统MPPT仿真研究[J]. 电子测量技术, 2022, 45(7): 75-81.