|
|
|
发布时间: 2023-12-28 |
综合能源 |
|
|
|
收稿日期: 2023-08-23
基金项目: 上海市科技创新行动计划(21DZ1207300)
中图法分类号: TP18;TU995
文献标识码: A
文章编号: 2096-8299(2023)06-0571-07
|
摘要
提出了一种基于改进Informer的蒸汽管网流量预测模型Informer_BEST。该模型通过引入扩展的因果卷积、相对位置和季节特征编码以及梯度中心化技术等3种算法,对Informer模型进行了改进和优化。对5种预测模型进行实验,结果表明,所提出的Informer_BEST预测模型展现了令人满意的测试结果,预测曲线与实际数据的变化趋势相吻合,对供热调度决策具有良好的指导作用。
关键词
蒸汽管网流量; Informer模型; 扩展的因果卷积网络; 相对位置编码; 梯度中心化技术
Abstract
The paper proposes an improved steam network flow prediction model, Informer_BEST, based on enhancements to the Informer model.This model has been enhanced and optimized by incorporating three algorithms into the Informer model: extended causal convolution, gradient centralization techniques, and the encoding of relative position and seasonal features.The paper conducts comparison between 5 predictive models.The experimental results indicate that the predictive model based on the improved Informer_BEST demonstrates satisfactory test outcomes.The predicted curve aligns with the changing trend of actual data, providing valuable guidance for predict heating scheduling decisions.
Key words
steam network flow; informer model; dilated causal convolutional neural network; relative position encoding; gradient centralization technique
蒸汽是综合能源系统的重要能源之一, 广泛应用于企业生产和日常生活中[1]。对蒸汽管网流量(以下简称“蒸汽流量”)和压力进行合理有效预测, 有助于维持整个系统能源资源平衡, 减少能源浪费[2]。蒸汽管网具有能源设备多、流量变化快等特点[3], 难以根据其机理建立蒸汽流量预测模型。随着自动化和数据库技术的进步, 实现了对历史实时数据的及时采集, 使得建立数据驱动的蒸汽流量预测模型成为可能[4]。目前, 应用最广泛的预测方法是BP(Back Propagation)神经网络。但传统的BP算法存在局部最优陷阱问题, 泛化能力一般[5]。循环神经网络(Recurrent Neural Network, RNN)在深度学习中可以适应连续时间步骤之间的依赖关系[6], 但容易出现梯度消失或爆炸问题。长短期记忆网络(Long Short-Term Memory, LSTM)通过引入门控单元来解决梯度问题, 提高了预测模型的效率和稳定性[7-8]。文献[9-10]分析了基于LSTM模型在短期电力负荷预测方面的性能。然而, 在某些应用场景中, 需要利用大量历史时间序列数据进行长期预测。由于传统LSTM只能通过逐步递归的方式获取全局信息, 很难捕捉到长期依赖关系, 因此LSTM模型的效果可能会受到限制[11]。
Transformer模型作为一种深度学习模型[12], 在自然语言处理和计算机视觉领域取得了广泛的应用。但其存在时间复杂度高、内存利用率高以及在时间序列预测中会出现预测率骤降等问题, 无法直接应用于时间序列预测, 因此研究人员对其进行了一些改进。文献[13]考虑了注意力矩阵的稀疏分解。文献[14]提出了一种新的自注意力机制, 以降低时空复杂度。文献[15]提出了Transformer的变体Informer, 并在4个大规模数据集上进行了测试, 验证了其出色的性能。这些研究为时间序列预测问题提供了一种不同的解决方案。文献[16]将Informer模型应用于电机轴承震动时间序列预测任务中, 得到了令人满意的预测结果。文献[17]将Informer模型成功应用于风力发电预测领域。文献[18]将Informer模型与卷积神经网络模型相结合, 成功应用于锂离子电池充电桩的电荷状态估计领域。
综上所述, Informer被认为是目前较为先进的时间序列预测模型。为了研究Informer在蒸汽流量预测中的性能, 本文选择上海闵行区某供热管网采集的蒸汽管网数据作为研究对象, 并以日期、温度、天气数据、历史蒸汽压力和历史蒸汽流量作为输入特征, 将Informer模型应用于蒸汽流量预测任务。通过引入3种算法, 对Informer模型进行改进, 并最终提出了Informer_BEST模型。
1 相关理论介绍
1.1 Transformer模型简介
作为一种革命性的序列建模方法, Trans-former模型采用了编码器-解码器结构。通过自注意力机制的运用, Transformer模型在各种任务中展现出了卓越的性能。
自注意力机制是通过3个权重矩阵将序列中每个元素转化为3个不同功能的矩阵, 分别为查询矩阵Q、键矩阵K和值矩阵V。其中, Q∈RLQ×d, K∈RLK×d, V∈RLV×d, d为输入维度, LQ、LK、LV分别为Q、K、V的行维度。通过计算K与Q的相似度, 为每个查询矩阵赋予相应的重要性分数, 并利用这些分数对V进行加权, 从而实现对上下文信息特征的有效融合。
自注意力机制的公式为
| $ O=A(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\boldsymbol{V} \cdot S\left(\frac{\boldsymbol{Q} \cdot \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d}}\right) $ | (1) |
式中: O——自注意力机制输出;
A(·)——自注意力计算函数;
S(·)——Softmax计算函数。
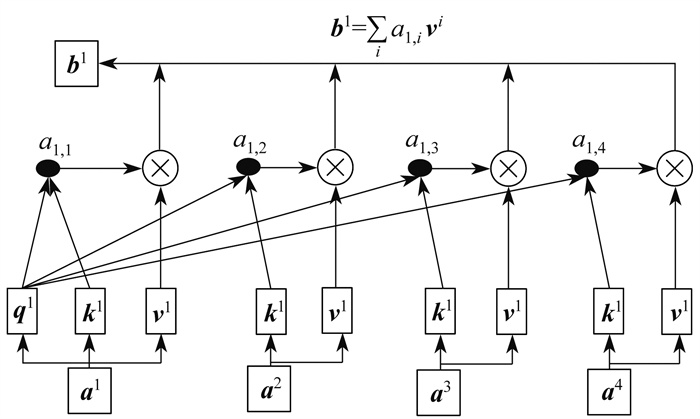
自注意力机制的具体计算流程如图 1所示。其中, b1为经过自注意力机制计算后的输出序列列向量, ax为输入序列x列的列向量, qx、kx、vx分别为输入序列x列对应的查询向量、键向量和值向量, αx, y为ax和ay的相关性分数。
编码器由多个相同的自注意力模块堆叠而成, 每个自注意力模块包含自注意力层和前馈神经网络2个子层。解码器也由多个自注意力模块堆叠而成, 与编码器略有不同, 每个解码器的自注意力模块包含自注意力层、编码器-解码器注意力层和前馈神经网络3个子层。
1.2 Informer模型简介
Informer模型是一种基于Transformer模型的时间序列预测模型。为了提高在长序列时间预测(Long Sequence Time Series Forecasting, LSTF)问题中的预测能力, 相较于传统Transformer模型, Informer模型进行了如下改进: 提出了ProbSparse自注意力算法, 只允许关注重要查询矩阵, 以提高运算效率; 在编码器内设计了自注意力蒸馏结构, 该结构利用卷积网络来连接两个自注意力模块, 可实现输出长度下采样, 并进一步提高运算效率; 针对传统解码器在推理阶段中误差的累计传播问题, Informer提出了生成式推理解码器, 该解码器通过一个前向过程即可生成完整的长序列预测结果。
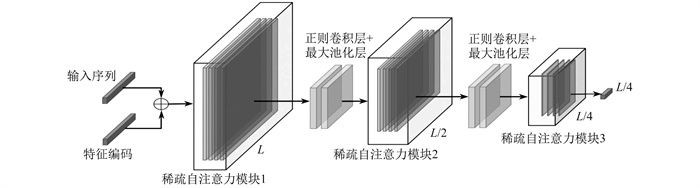
Informer编码器中的自注意力蒸馏结构如图 2所示, 其中L为输入序列长度。
从j层到j+1层的蒸馏过程公式为
| $ L_{j+1}=M\left(E\left(C\left(\left[L_j\right]_{\mathrm{AB}}\right)\right)\right) $ | (2) |
式中: Lj、Lj+1——第j层和第j+1层自注意力模块输入;
M(·)——最大池化层函数;
E(·)——激活函数;
C(·)——卷积网络函数;
[·]AB——自注意力模块。
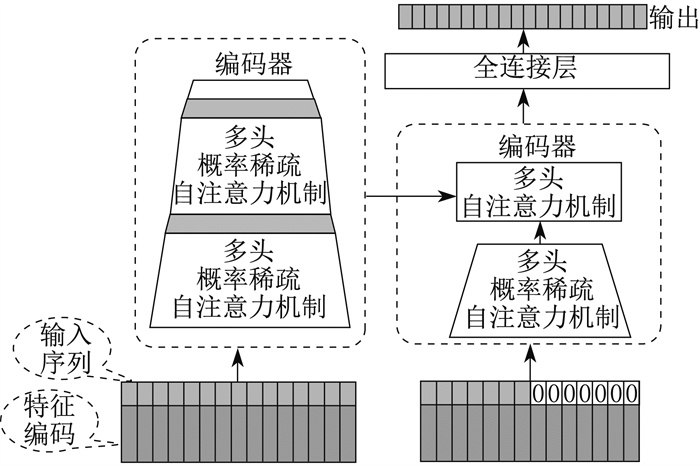
Informer模型结构如图 3所示。
2 Informer模型的改进
本文引入以下3种算法, 对Informer模型进行改进: 第1种为扩展的因果卷积扩展的因果卷积(Dilated Causal Convolutional Network, DCCN)网络, 取代了Informer蒸馏结构中的正则卷积网络, 模型记为Informer_DCC; 第2种为相对位置编码方法, 将其与季节特征编码相结合, 作为Informer模型的编码输入特征, 模型记为Informer_REL; 第3种为梯度中心化(Gradient Centralization, GC)技术, 将其嵌入到Adam优化器中, 以改进模型的训练过程, 模型记为Informer_GC。
2.1 扩展的因果卷积网络
正则卷积层在时间序列预测中存在两个主要缺陷: 一是在网络深度增加时只能回顾有限的历史数据, 在处理极长序列时效果有限; 二是正则卷积层没有考虑时间视角, 这可能导致未来信息的泄露。基于DCCN在时间序列预测任务中的优点[19-20], 本文采用DCCN替代传统的正则卷积, 以应对时间序列预测中正则卷积网络存在的缺陷。DCCN在时间序列预测中具有独特的优势。它通过扩大卷积核的接受域, 使得模型可以更好地捕捉长期的依赖关系。同时, 因果卷积保持了时间维度上的因果性, 避免了未来信息泄露的问题, 确保了模型在时间序列预测任务中的有效性和可靠性。
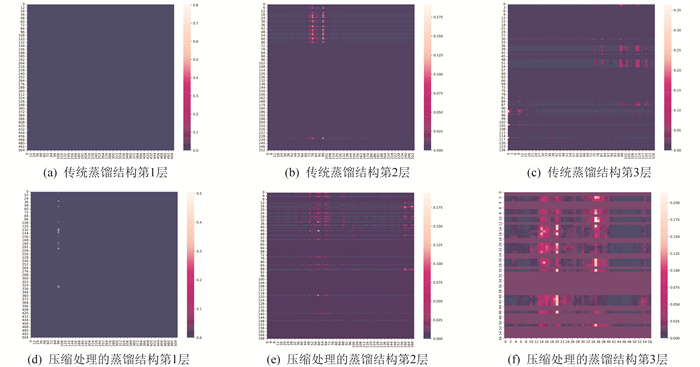
蒸馏结构通过在每两个自注意力模块之间插入卷积层和最大池化层来修剪输入长度, 为后一个自注意力模块提供更紧凑的特征映射。为了进一步提升模型的性能和预测准确性, 本文对蒸馏结构中的输出下采样进了压缩处理, 将其压缩为输入序列长度的1/3。蒸馏结构自注意力层中Q和K的相关性热力图如图 4所示。
图 4(a)~(c)显示了传统蒸馏结构下每一层自注意力模块中Q和K的相关性, 而图 4(d)~(f)显示了使用输出下采样压缩处理方法后的Q和K相关性。通过对比可以清晰地观察到, 压缩处理后蒸馏结构的效果更好、效率更高, 保持了大部分特征的完整性, 而且所提取的特征更加明显和集中。
2.2 相对位置编码及季节特征编码
2.2.1 相对位置编码
为了将自注意力机制无法捕捉的序列顺序信息纳入模型, 传统Informer模型采用位置编码作为模型的输入特征之一。位置编码公式为
| $ \boldsymbol{P}_{\mathrm{E}}\left(p_{\mathrm{S}}, 2 i\right)=\sin \left(\frac{p_{\mathrm{S}}}{10000^{\frac{2 i}{d}}}\right) $ | (3) |
| $ P_{\mathrm{E}}\left(p_{\mathrm{S}}, 2 i+1\right)=\cos \left(\frac{p_{\mathrm{S}}}{10000^{\frac{2 i}{d}}}\right) $ | (4) |
式中: PE——二维向量, 用于保存位置编码信息;
pS——元素在输入序列中的位置, pS=0, 1, 2, …, L-1;
i——在输入序列维度d上的索引。
将位置编码加入到自注意力机制, 计算公式为
| $ \left[\boldsymbol{W}_{\mathrm{q}}\left(\boldsymbol{E}_{x_i}+\boldsymbol{U}_i\right)\right]\left[\boldsymbol{W}_{\mathrm{k}}\left(\boldsymbol{E}_{x_j}+\boldsymbol{U}_j\right)\right]^{\mathrm{T}} $ | (5) |
式中: Ai, j——加入位置编码信息的自注意力机制计算量;
Wq、Wk——Q和K的权重矩阵;
xi、xj——权重矩阵中第i个和第j个位置的元素;
Exi、Exj——xi和xj的数据嵌入向量;
Ui、Uj——第i个和第j个位置的位置嵌入向量。
因式分解后得到:
| $ \begin{aligned} & A_{i, j}= \underbrace{\boldsymbol{E}_{x_i} \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}}^{\mathrm{T}} \boldsymbol{E}_{x_i}^{\mathrm{T}}}_{(\mathrm{a})}+\underbrace{\boldsymbol{E}_{x_i} \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}}^{\mathrm{T}} \boldsymbol{U}_j^{\mathrm{T}}}_{(\mathrm{b})}+ \\ & \underbrace{\boldsymbol{U}_i \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}}^{\mathrm{T}} \boldsymbol{E}_{x_j}^{\mathrm{T}}}_{(\mathrm{c})}+\underbrace{\boldsymbol{U}_i \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}}^{\mathrm{T}} \boldsymbol{U}_j^{\mathrm{T}}}_{(\mathrm{d})} \end{aligned} $ | (6) |
其中, (a)中没有位置向量; (b)和(c)中都只有1个位置向量, 不包含相对位置信息; (d)中包含2个位置向量, 有可能包含相对位置信息, 但加入未知线性变换(WqWkT)后, 所包含的相对位置信息将会消失[21]。为了解决这一问题, 文献[22]引入相对位置编码方法, 将式(6)转化为
| $ \begin{aligned} A_{i, j}= & \underbrace{\boldsymbol{E}_{x_i} \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}, \mathrm{E}}^{\mathrm{T}} \boldsymbol{E}_{x_i}^{\mathrm{T}}}_{(\mathrm{a})}+\underbrace{\boldsymbol{E}_{x_i} \boldsymbol{W}_{\mathrm{q}} \boldsymbol{W}_{\mathrm{k}}^{\mathrm{T}} \boldsymbol{R}_{i-j}^{\mathrm{T}}}_{(\mathrm{b})}+ \\ & \underbrace{\boldsymbol{u} \boldsymbol{W}_{\mathrm{k}, \mathrm{E}}^{\mathrm{T}} \boldsymbol{E}_{x_j}^{\mathrm{T}}}_{(\mathrm{c})}+\underbrace{\boldsymbol{v} \boldsymbol{W}_{\mathrm{k}, \mathrm{R}}^{\mathrm{T}} \boldsymbol{R}_{i-j}^{\mathrm{T}}}_{(\mathrm{d})} \end{aligned} $ | (7) |
式中: Wk, E、Wk, R——键矩阵k基于数据和基于位置分离的键向量;
Ri-j——第i个和第j个位置的相对位置信息嵌入向量;
u、v——不包含位置信息的可学习参数向量,u∈Rd, v∈Rd。
其中, UjT被Ri-jT代替, 表示将K(xj)上的绝对位置信息改为相对于Q(xi)的相对位置信息。UiWq表示与Q相关的绝对位置向量, 改为相对位置后Q便与自身位置无关, 故被不包含位置信息的可学习参数向量u和v代替。
2.2.2 季节特征编码
时间序列预测问题中, 是否充分挖掘时间信息特征, 对于预测结果的影响十分重大。因此, 本文将时间数据分解为年、月、日、周、季节、节假日, 采用Trigonometric编码方式进行特征编码, 并融合相对位置编码共同作为模型的输入特征编码。
2.3 GC技术
Adam优化器在深度学习领域被广泛应用。它能够根据梯度的变化情况动态调整学习率的大小, 但缺点是过度依赖学习率调整和对小批量样本的不稳定性等。为了解决这些问题, 本文引入了GC技术来改进Adam优化器。GC技术最初由YONG H W等人[23]于2020年提出, 核心思想是将梯度集中到均值为零的位置, 以避免梯度分布的不稳定性。通过对梯度的中心化处理, GC技术能够消除不同参数之间的相关性, 使得训练过程更加平稳, 并减少过拟合的风险。
假设梯度是通过反向传播得到, 则对于梯度为▽wiZ(i=1, 2, 3, …, l)的权重向量wi, GC的作用过程可用ΦGC表示。其公式为
| $ \Phi_{\mathrm{GC}}\left(\nabla \boldsymbol{w}_i \boldsymbol{Z}\right)=\nabla \boldsymbol{w}_i \boldsymbol{Z}-\mu \nabla \boldsymbol{w}_i \boldsymbol{Z} $ | (8) |
| $ \mu \nabla \boldsymbol{w}_i \boldsymbol{Z}=\frac{1}{m} \sum\limits_{i=1}^m \nabla \boldsymbol{w}_{i, j} \mathbf{Z} $ | (9) |
式中: Z——目标函数;
wi——权重矩阵W∈Rm×n的第i列权重向量。
因此, 只需要计算权重矩阵列向量的均值, 然后去除每个列向量的均值。
3 实验过程与结果分析
3.1 实验准备
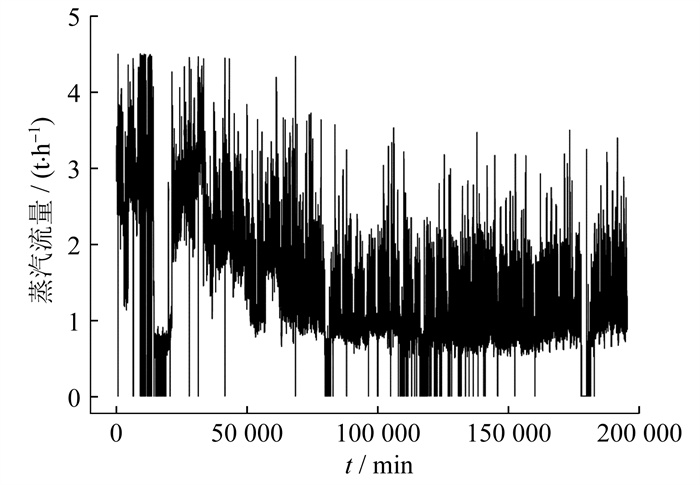
实验数据来自上海闵行区某供热管网采集系统, 包含2019年10月1日至2020年9月15日各用户信息。流量预测对象为系统中的某化工公司, 采样间隔设为2 min, 数据总数为18万。该化工公司的历史蒸汽流量如图 5所示。
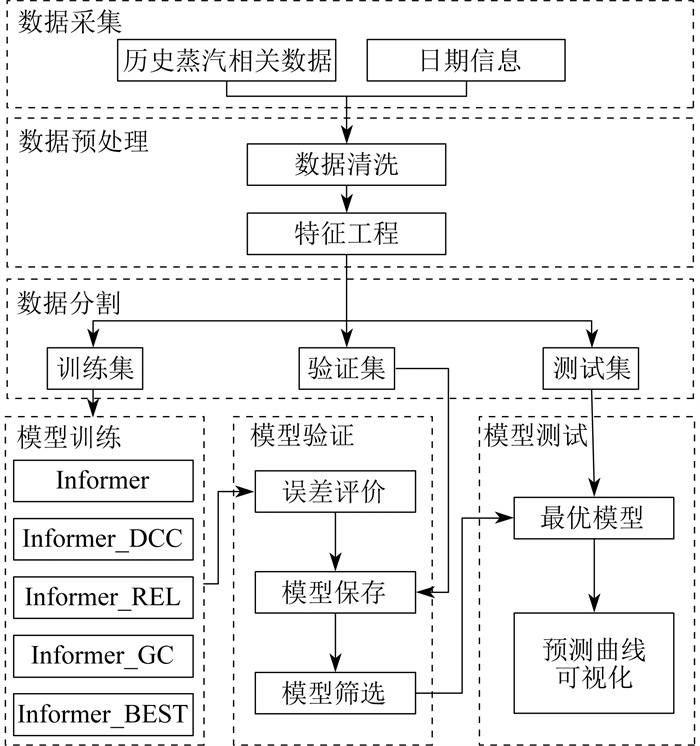
蒸汽流量预测模型的实验框架如图 6所示。其中, Informer_BEST模型为同时应用3种改进算法的模型。
在实验框架中, 首先进行了数据预处理。由于数据采集可能受多种因素的影响, 本文采用箱线图法来检测和排除历史蒸汽流量及特征中的异常值, 并使用线性插值来填充缺失值。特征之间的数值范围差异较大, 因此对数据进行了零均值归一化处理。通过数据预处理和相关性分析可以获得5个特征变量, 包括日期、温度、天气、蒸汽压力和瞬时蒸汽流量。其中, 日期列可作为时间信息输入到目标模型中。将数据分割成训练集、验证集和测试集时, 采用传统的7∶ 1.5∶ 1.5的数据分割比例。在模型训练阶段, 使用传统的Informer模型以及经过优化的Informer模型, 在相同数据集上采用相同的超参数进行训练, 并将预测结果进行记录和保存。
在模型验证阶段, 采用误差评价方法对各个模型的预测结果进行对比分析, 以确定性能最佳的模型。误差评价方法包括平均绝对误差EMA、均方误差EMS和均方根误差ERMS等指标, 具体公式为
| $ E_{\mathrm{MA}}=\frac{1}{N} \sum\limits_{n=1}^N\left|t_n-y_n\right| $ | (10) |
| $ E_{\mathrm{MS}}=\frac{1}{N} \sum\limits_{n=1}^N\left(t_n-y_n\right)^2 $ | (11) |
| $ E_{\mathrm{RMS}}=\sqrt{\frac{1}{N} \sum\limits_{n=1}^N\left(t_n-y_n\right)^2} $ | (12) |
式中: N——预测总数, 即预测序列长度;
tn——实际流量值;
yn——预测流量值。
3.2 实验结果分析
在相同的数据集上, 本文将传统的Informer模型与优化后的Informer模型进行了对比实验。其中对3种改进方法进行了消融实验, 实验中, 为5种模型设置了相同的超参数, 如表 1所示。
表 1
模型超参数
| 参数 | 描述 | 数值 |
| enc_in | 编码器输入尺寸 | 5 |
| dec_in | 解码器输入尺寸 | 5 |
| c_out | 输出尺寸 | 1 |
| seq_len | 编码器输入序列长度 | 512 |
| dec_len | 解码器起始序列长度 | 208 |
| pred_len | 预测序列长度 | 720 |
| e_layers | 编码器层数 | 3 |
| d_layers | 解码器层数 | 1 |
| d_model | 模型尺寸 | 512 |
| learning_rate | 优化器学习率 | 0.000 1 |
| embed | 时间特征编码类型 | fixed |
| itr | 实验次数 | 5 |
| train_epoch | 训练迭代次数 | 6 |
各个模型在同一数据集上的评价结果如表 2所示。其中, 将最佳结果用粗体字标识。
表 2
模型评价结果
| 模型 | EMA | EMS | ERMS |
| Informer | 0.024 | 0.106 | 0.157 |
| Infromer_DCC | 0.019 | 0.087 | 0.137 |
| Informer_REL | 0.016 | 0.076 | 0.125 |
| Informer_GC | 0.021 | 0.095 | 0.145 |
| Informer_BEST | 0.010 | 0.056 | 0.102 |
由表 2可以看出, 3种方法对Informer模型的性能都有不同程度的提升。其中, 引入相对位置和季节特征编码的方法对模型性能的提升效果最为显著, 融合了3种改进方法的Informer_BEST模型在性能方面的总体表现最为出色。
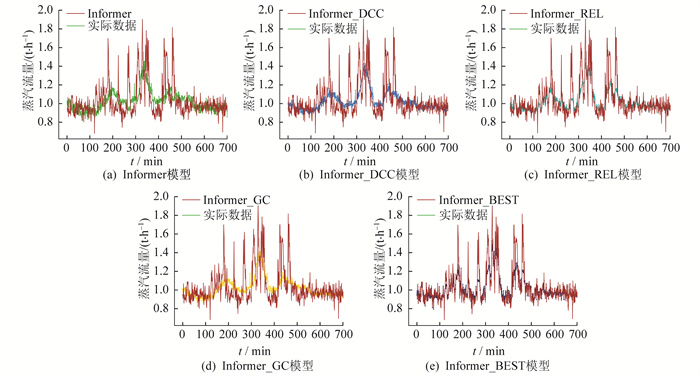
5种模型的预测曲线如图 7所示。
由图 7可以看出, 5种模型都成功地预测了实际数据的趋势, 并且没有出现时间延迟问题。但相较于传统的Informer模型, Informer_BEST模型在拟合实际数据方面表现更好, 这将对供热管网蒸汽调度提供很大的帮助。需要指出的是, 这些模型在拟合实际数据中跳跃性较大的部分仍存在一定的不足。
4 结语
本文将时间序列预测模型Informer应用于蒸汽管网预测领域, 并引入了3种方法来改进Informer模型, 进而提出了Informer_BEST模型。为了突出改进方法的有效性, 对Informer_BEST模型进行了消融实验, 并采用3种误差评价指标对实验结果进行了评价和分析。根据实验结果可知, Informer模型在供热管网蒸汽预测任务中表现良好, 能够成功预测实际数据趋势, 但在拟合实际数据方面存在一定的欠缺。通过使用3种方法改进模型, 这一缺陷得到了改善。其中, 相对位置和季节特征编码的改进方法表现最为突出, 而且在解决拟合实际数据缺陷方面具有显著效果。模型预测效果的提升对供热管网蒸汽调度能够起到积极的指导作用, 对于提高系统的安全性、减少能源浪费以及促进节能减排具有重要意义。
参考文献
-
[1]欧阳英姿, 万勇. 蒸汽介质分析及蒸汽计量系统综述[J]. 仪器仪表标准化与计量, 2021(1): 28-31. DOI:10.3969/j.issn.1672-5611.2021.01.013
-
[2]ZHAO L, YE Z, DU W. Multi-objective optimization of steam system based on GPU acceleration[J]. IFAC-Papers On Line, 2018, 51(21): 183-188. DOI:10.1016/j.ifacol.2018.09.415
-
[3]LV Z, LIU Y, ZHAO J, et al. Bayesian neural networks based pipeline pressure prediction for steam system in steel industry[C]//2013 5th International Conference on Modelling, Identification and Control. IEEE, 2013: 344-349.
-
[4]LIU Y, LIU Q, WANG W, et al. Data-driven based model for flow prediction of steam system in steel industry[J]. Information Sciences, 2012, 193: 104-114. DOI:10.1016/j.ins.2011.12.031
-
[5]YANG X C, HOU Y B, KONG L H. The coal slurry pipeline pressure prediction research based on quantum genetic BP neural network[J]. Applied Mechanics and Materials, 2013, 336: 722-727.
-
[6]杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(增刊2): 1-6.
-
[7]GREFF K, SRIVASTAVA R K, KDUTNIK J, et al. LSTM: a search space odyssey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(10): 2222-2232. DOI:10.1109/TNNLS.2016.2582924
-
[8]张宇晨, 姜雪松, 李春伟, 等. 基于Bootstrap误差修正的电力负荷短期预测深度学习模型[J]. 热力发电, 2023, 52(3): 121-129.
-
[9]KONG W, DONG Z Y, HILL D J, et al. Short-term residential load forecasting based on resident behaviour learning[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1087-1088. DOI:10.1109/TPWRS.2017.2688178
-
[10]SON N, YANG S, NA J. Deep neural network and long short-term memory for electric power load forecasting[J]. Applied Sciences, 2020, 10(18): 6489. DOI:10.3390/app10186489
-
[11]LI S, JIN X, XUAN Y, et al. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc, 2019: 471.
-
[12]VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc, 2017: 6000-6010.
-
[13]CHILD R, GRAY S, RADFORD A, et al. Generating long sequences with sparse transformers[EB/OL]. (2019-04-23)[2023-08-20]. https://doi.org/10.48550/arXiv.1904.10509.
-
[14]WANG S, LI B Z, KHABSA M, et al. Linformer: self-attention with linear complexity[EB/OL]. (2020-06-14)[2023-08-20]. https://doi.org/10.48550/arXiv.2006.04768.
-
[15]ZHOU H, ZHANG S, PENG J, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Washington, DC: AAAI Press, 2021: 11106-11115.
-
[16]YANG Z, LIU L, LI N, et al. Time series forecasting of motor bearing vibration based on informer[J]. Sensors, 2022, 22(15): 5858. DOI:10.3390/s22155858
-
[17]HUANG X, JIANG A. Wind power generation forecast based on multi-step informer network[J]. Energies, 2022, 15(18): 6642. DOI:10.3390/en15186642
-
[18]ZOU R, DUAN Y, WANG Y, et al. A novel convolutional informer network for deterministic and probabilistic state-of-charge estimation of lithium-ion batteries[J]. Journal of Energy Storage, 2023, 57: 106298. DOI:10.1016/j.est.2022.106298
-
[19]BAI S, KOLTER J Z, KOLTUN V. Convolutional sequence modeling revisited[C]//Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview. net, 2018: 4-6.
-
[20]SHEN L, WANG Y. TCCT: tightly-coupled convolutional transformer on time series forecasting[J]. Neurocomputing, 2022, 480: 131-145. DOI:10.1016/j.neucom.2022.01.039
-
[21]YAN H, DENG B, LI X, et al. TENER: adapting transformer encoder for named entity recognition[J]. (2019-11-10)[2023-08-20]. https://doi.org/10.48550/arXiv.1911.04474.
-
[22]DAI Z, YANG Z, YANG Y, et al. Transformer-XL: attentive language models beyond a fixed-length context[C]//Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics. Florence: ACL, 2019: 4-5.
-
[23]YONG H W, HUANG J, HUA X, et al. Gradient centralization: a new optimization technique for deep neural networks[C]//Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020: 635-652.