|
|
|
发布时间: 2023-12-28 |
综合能源 |
|
|
|
收稿日期: 2023-03-30
中图法分类号: TM614;TK91
文献标识码: A
文章编号: 2096-8299(2023)06-0563-08
|
摘要
针对含电制氢综合能源系统规划问题,为了充分考虑综合能源系统的低碳性,提出了一种计及碳超额率的阶梯式碳交易的含电制氢综合能源系统规划方法。首先,建立了计及碳超额率的阶梯式碳交易模型。然后,以年运行成本最小和碳排放量最低为目标函数,建立了基于计及碳超额率的阶梯式碳交易的含电制氢综合能源系统规划模型,对含电制氢综合能源系统进行最优配置。最后,通过仿真验证了计及碳超额率的阶梯式碳交易机制的低碳性、适用性和经济性,并讨论了碳交易参数与系统规划之间的相互耦合影响。
关键词
含电制氢综合能源系统; 阶梯式碳交易机制; 碳超额率; 碳交易区间数目
Abstract
Aiming at the planning of integrated energy system including power to hydrogen, a planning method for hydrogen containing integrated energy system considering stepwise carbon trading with carbon excess rate is proposed in order to fully consider the low-carbon characteristics.First, a stepped carbon trading model considering carbon excess rate is established.Then, a planning model of the integrated energy system including power to hydrogen based on stepped carbon trading considering carbon excess rate is established with the minimum annual operating cost and the lowest carbon emission as the objective function, so as to make the optimal decision on the equipment configuration.Through simulation, the economics, low-carbon characteristics and applicability of the stepped carbon trading mechanism considering the carbon excess rate and the coupling effects of carbon trading parameters on system planning are discussed.
Key words
integrated energy system including power to hydrogen; stepped carbon trading mechanism; carbon excess rate; number of carbon trading bands
在全球环境问题日益凸显的背景下, 节能减排成为世界各国共识, 我国提出“30·60”的“双碳”发展目标[1]。在“双碳”目标下, 能源行业正逐步向清洁低碳结构转型。含电制氢综合能源系统是将冷、热、电、气等子系统组合起来的系统[2-4]。世界范围内具有代表性的综合能源项目之一是德国的E - Energy项目。该项目选定了6个城市进行试点, 侧重于能源系统和信息系统的集成, 通过实时的数据共享, 实现能量的梯级利用, 提高了能源利用率。如何建设含电制氢综合能源系统, 是助力我国实现“30·60”的双碳目标的有效途径。其中低碳设备的合理配置可以在保证经济性的同时降低碳排放量。
目前已有学者针对含电制氢综合能源系统规划问题进行研究。文献[5]提出了一种考虑风光利用率和含氢能流的多能流综合能源系统规划方法, 对比分析了含氢能流和含蓄电池的综合能源系统的新能源消纳能力及经济性, 结果表明含氢能流综合能源系统性能更好。文献[6]提出了考虑储氢物理特性和氢能多模式利用的区域综合能源系统中长期优化运行方法, 通过仿真结果表明采用氢能多模式利用可有效应对季节性供需不平衡问题, 提高了系统运行的经济性和新能源的消纳水平。文献[7]提出一种考虑电热柔性负荷及氢能精细化建模的含氢综合能源低碳运行方法, 具体研究了氢能利用各环节所涉及能源设备的能源特性, 进行氢能利用精细化建模, 仿真结果表明精细化建模比线性化建模具有更好的经济性和低碳性。上述研究中将氢能流引入综合能源系统, 有效实现了系统的低碳经济运行。
碳交易机制是减少碳排放量并兼顾经济性的有效手段。政府下发给企业一定的免费碳配额, 当企业的碳排放超标时, 需要去市场上购买碳配额。目前上海已经开始试行碳交易市场。上海市生态环境局发布了《上海市2021年碳排放配额分配方案》, 对所有纳入碳交易配额管理的单位发放碳排放配额。碳交易机制已经逐步成为引导综合能源系统降低碳排放的重要手段之一[8-10]。文献[11]提出了一种基于阶梯式碳交易的园区综合能源系统多阶段规划方法, 研究了阶梯式碳交易的区间长度对碳排放量的影响。文献[12]考虑了电转气设备和光伏设备的全寿命周期碳排放, 提出了一种计及综合能源系统全寿命周期碳排放和碳交易机制的电转气设备和光伏容量联合配置方法。
在上述研究的基础上, 本文设计了一种新的碳交易机制, 将碳超额率引入阶梯式碳交易模型, 构建了计及碳超额率的阶梯式碳交易模型。首先, 构造以年运行成本最小和碳排放量最低为目标函数的含电制氢综合能源系统规划模型; 然后, 分别对碳超额量和碳超额率两种阶梯式碳交易机制下的含电制氢综合能源系统规划方案进行对比研究; 最后, 通过不同情景下的案例对比验证计及碳交易率的阶梯式碳交易机制模型的优越性。
1 含电制氢综合能源系统模型
含电制氢综合能源系统内部有许多灵活性的设备, 通过调整设备的出力, 可以达到低碳运行的目的。
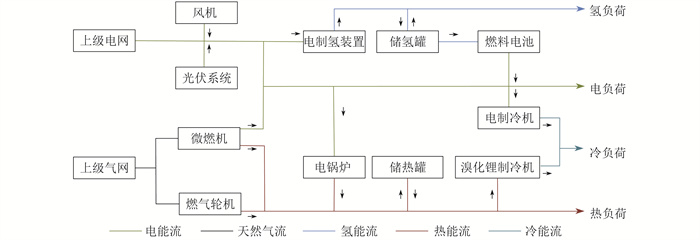
含电制氢综合能源系统结构如图 1所示。主要由电力子系统、氢气子系统、燃气子系统组成。其中电力子系统主要由风机、光伏系统、电锅炉、电制冷机组成; 氢气子系统主要由电制氢装置、储氢罐及燃料电池组成; 燃气子系统主要由微燃机、燃气轮机、溴化锂制冷机、储热罐组成。
2 阶梯式碳交易机制
2.1 碳排放配额
在碳交易机制下, 政府分配的碳排放额与实际碳排放量存在差异, 碳排放量是一种可以进行自由交易的商品, 而在电力行业, 目前我国主要采用无偿的方式进行初始碳排放额的分配。本文采用的行业基准线法来确认系统的碳排放配额。碳排放源有外购电、微燃机以及燃气锅炉, 其碳排放配额和实际碳排放量公式分别为
| $ E_{\text {total }}=E_{\mathrm{EN}}+E_{\mathrm{MT}}+E_{\mathrm{GB}} $ | (1) |
| $ E_{\mathrm{EN}}=\eta_{\mathrm{e}} \sum\limits_{t=1}^T \lambda P_{\mathrm{EN}, t} $ | (2) |
| $ E_{\mathrm{MT}}=\eta_{\mathrm{h}} \sum\limits_{t=1}^T\left(\eta_{\mathrm{e}, \mathrm{h}} \mid P_{\mathrm{MT}, t}+H_{\mathrm{MT}, t}\right) $ | (3) |
| $ E_{\mathrm{GB}}=\eta_{\mathrm{h}} \sum\limits_{t=1}^T H_{\mathrm{GB}, t} $ | (4) |
| $ E_{\mathrm{total}, \mathrm{a}}=E_{\mathrm{EN}, \mathrm{a}}+E_{\mathrm{MT}, \mathrm{a}}+E_{\mathrm{GB}, \mathrm{a}} $ | (5) |
| $ E_{\mathrm{EN}, \mathrm{a}}=\eta_{\mathrm{e}, \mathrm{a}} \sum\limits_{t=1}^T \lambda P_{\mathrm{EN}, t} $ | (6) |
| $ E_{\mathrm{MT}}=\eta_{\mathrm{h}, \mathrm{a}} \sum\limits_{t=1}^T\left(\eta_{\mathrm{e}, \mathrm{h}} P_{\mathrm{MT}, t}+H_{\mathrm{MT}, t}\right) $ | (7) |
| $ E_{\mathrm{GB}}=\eta_{\mathrm{h}, \mathrm{a}} \sum\limits_{t=1}^T H_{\mathrm{GB}, t} $ | (8) |
式中: Etotal、EEN、EMT、EGB——综合能源系统、外购电、微燃机、燃气锅炉的碳排放配额量;
ηe——供能设备单位电功率的碳排放权配额, 取0.728 t/MWh;
T——规划总时间数, 取8 760 h;
λ——外购电中的煤发电所占的比例, 取0.8;
PEN, t——t时段外购电量;
ηh——供能设备单位热功率的碳排放权配额, 取0.102 t/GJ;
ηe, h——电、热功率折算参数, 取6 MJ/kWh;
PMT, t——t时段微燃机输出的电功率;
HMT, t、HGB, t——t时段微燃机、燃气锅炉的输出热功率;
Etotal, a、EEN, a、EMT, a、EGB, a——综合能源系统、外购电、微燃机、燃气锅炉的实际碳排放量;
ηe, a——供能设备单位电功率的实际碳排放系数, 取1.08 t/MWh;
ηh, a——供能设备单位热功率的实际碳排放系数, 取0.065 t/GJ。
2.2 阶梯式碳交易模型
阶梯式碳交易以一定量的碳排放量为区间长度, 划分多个交易区间, 随着超额碳排放量的增加, 交易区间的碳交易价格也会随之升高。阶梯式碳交易成本计算模型如下
| $ {c_{{\rm{c}}{{\rm{o}}_2}}} = \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{C}}{{\rm{O}}_2}}}\left( {{E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}}} \right),}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{0 \le l{\rm{ < }}{E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}}}\\ {{c_{{\rm{C}}{{\rm{O}}_2}}}l + (1 + \alpha ){c_{{\rm{C}}{{\rm{O}}_2}}}\left( {{E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}} - l} \right),}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{l \le {E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}}{\rm{ < }}2l}\\ {{c_{{\rm{C}}{{\rm{O}}_2}}}(2 + \alpha )l + (1 + 2\alpha ){c_{{\rm{C}}{{\rm{O}}_2}}}\left( {{E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}} - 2l} \right),}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{2l \le {E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}}{\rm{ < }}3l}\\ {{c_{{\rm{C}}{{\rm{O}}_2}}}(3 + 3\alpha )l + (1 + 3\alpha ){c_{{\rm{C}}{{\rm{O}}_2}}}\left( {{E_{{\rm{total}},,{\rm{a}}}} - {E_{{\rm{total}}}} - 3l} \right),}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{3{l_d} \le {E_{{\rm{total}},{\rm{a}}}} - {E_{{\rm{total}}}}{\rm{ < }}4l} \end{array}} \right. $ | (9) |
式中: CCO2——阶梯式碳交易成本;
cCO2——碳交易单价;
l——碳排放区间长度;
α——价格增长的幅度。
阶梯式碳交易模型的碳交易单价f(Etotal, a-Etotal)和碳超额量(Etotal, a-Etotal)关系如图 2所示。
当有多个不同规模的含电制氢综合能源系统使用同一个阶梯式碳交易机制时, 如何确定碳交易区间长度就成为了问题。如果按照碳排放规模最大的综合能源系统去确认碳交易区间长度, 那确认后的碳交易区间长度对较小规模的综合能源系统来说会太长。碳交易区间长度过长时, 阶梯式碳交易机制对碳排放的约束力大幅度下降。
2.3 计及碳超额率的阶梯式碳交易模型
阶梯式碳交易模型的碳排放区间长度是按照超出碳排放配额的碳排放量来划分的。这样就无法清晰看出实际碳排放量超过碳配额的程度, 以及适用范围较窄。为了使得阶梯式碳交易模型更合理, 本文提出了一种碳排放程度衡量指标, 将实际碳排放量与碳排放配额的比例命名为碳超额率, 结合碳交易理论构建计及碳超额率的阶梯式碳交易模型。
计及碳超额率的阶梯式碳交易机制按照碳超额率划分为若干个区间, 各区间对应不同的碳交易价格。基于该碳交易机制, 当碳超额率大于1时, 综合能源系统需要支付费用购买碳排放权, 碳超额率的值越大, 对应区间的碳排放权购买单价越高。
碳超额率ξ公式如下:
| $ \xi=\frac{E_{\text {total, } \mathrm{a}}}{E_{\text {total }}} $ | (10) |
阶梯式碳交易成本计算模型如下:
| $ C_{\mathrm{CO}_2, \mathrm{~d}}=\left\{\begin{array}{l} c_{\mathrm{CO}_2}\left(E_{\text {total, }, \mathrm{a}}-E_{\text {total }}\right), \\ \;\;\;\;\;\;\;\;\;1 \leqslant \xi<1.1 \\ 0.1 c_{\mathrm{CO}_2} E_{\mathrm{total}}+(1+\alpha) c_{\mathrm{CO}_2} \cdot \\ \;\;\;\;\left(E_{\mathrm{total, a}}-1.1 E_{\mathrm{total}}\right), \\ \;\;\;\;\;\;\;\;\;1.1 \leqslant \xi<1.2 \\ 0.1 c_{\mathrm{CO}_2}(2+\alpha) E_{\text {total }}+(1+ \\ \;\;\;\;2 \alpha) c_{\mathrm{CO}_2}\left(E_{\text {total, a }}-1.2 E_{\mathrm{total}}\right), \\ \;\;\;\;\;\;\;\;\;1.2 \leqslant \xi<1.3 \\ 0.1 c_{\mathrm{CO}_2}(3+3 \alpha) E_{\mathrm{total}}+(1+ \\ \;\;\;\;3 \alpha) c_{\mathrm{CO}_2}\left(E_{\mathrm{total}, \mathrm{a}}-1.3 E_{\mathrm{total}}\right), \\ \;\;\;\;\;\;\;\;\;1.3 \leqslant \xi<1.4 \end{array}\right. $ | (11) |
式中: CCO2, d——计及碳超额率的阶梯式碳交易成本。
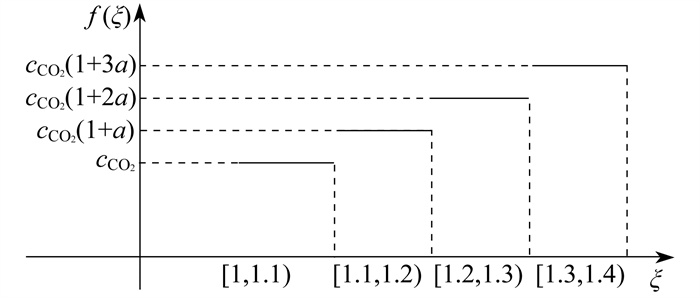
计及碳超额率的阶梯式碳交易模型的碳交易单价f(ξ)和碳超额率ξ关系如图 3所示。
3 含电制氢综合能源系统低碳规划模型
3.1 目标函数
本文以含电制氢综合能源系统为研究对象, 构造以系统投资运行成本最小为内层模型、碳排放量最低为外层模型的目标函数。具体描述如下:
| $ \begin{aligned} \min C_{\text {total }}= & C_{\text {inv }}+C_{\text {op }}+C_{\mathrm{EN}}+ \\ & C_{\text {fuel }}+C_{\mathrm{CO}_2, \mathrm{~d}} \end{aligned} $ | (12) |
| $ C_{\mathrm{inv}}=\sum\limits_{i=1}^N c_i \omega_i \frac{r_0\left(1+r_0\right)^{Y_i}}{\left(1+r_0\right)^{Y_i}-1} $ | (13) |
| $ C_{\mathrm{op}}=\sum\limits_{t=1}^T \sum\limits_{i=1}^N c_{\mathrm{op}, i} P_{i, t} \Delta t $ | (14) |
| $ C_{\mathrm{EN}}=\sum\limits_{t=1}^T e_{\mathrm{EN}, t} P_{\mathrm{EN}, t} \Delta t $ | (15) |
| $ C_{\text {fuel }}=\sum\limits_{t=1}^T\left(G_{\mathrm{GB}, t}+G_{\mathrm{MT}, t}\right) C_{\mathrm{gas}} $ | (16) |
式中: Ctotal、Cinv、Cop、CEN、Cfuel——年费用、设备等年值投资费用、运行维护费用、购电费用、购气费用;
N——设备种类;
ci——第i类设备的单位容量初始投资成本;
ωi——各类设备的配置容量;
r0——贴现率, 取6.7%;
Yi——第i类设备的全寿命周期;
cop, i——第i类设备的单位功率维护成本;
Pi, t——第i类设备在t时刻的出力;
Δt——功率维持不变时的时间变化量;
eEN, t——t时刻大电网的购电价格;
PEN, t——外购电在t时刻的出力;
GGB, t、GMT, t——t时段燃气锅炉、微燃机的燃气消耗量;
Cgas——天然气价格。
3.2 约束条件
3.2.1 容量约束条件
容量约束条件主要考虑保证系统正常运行所需的最低容量以及设备的占地面积。
| $ \omega_{i, \min } \leqslant \omega_i \leqslant \omega_{i, \max } \quad i \in I $ | (17) |
式中: ωi, min——为了保证系统正常运行的最低容量约束;
ωi, max——考虑占地面积的最大容量约束;
I——设备集, 包括WT、PV、EB、EC、HS、MT、GB、LBR、P2H、HT、FC。
3.2.2 功率平衡约束
为了保证综合能源系统的可靠运行, 系统必须满足电、热、气供需平衡, 即满足以下功率平衡方程。
| $ \begin{gathered} P_{\mathrm{EN}, t}+P_{\mathrm{WT}, t}+P_{\mathrm{PV}, t}+P_{\mathrm{FC}, t}+P_{\mathrm{MT}, t}= \\ P_{\mathrm{Load}, t}+P_{\mathrm{EB}, t}+P_{\mathrm{EC}, t}+P_{\mathrm{P} 2 \mathrm{H}, t} \end{gathered} $ | (18) |
| $ \begin{gathered} H_{\mathrm{MT}, t}+H_{\mathrm{GB}, t}+H_{\mathrm{FC}, t}+H_{\mathrm{EB}, t}+q_{\mathrm{TT}}^{\mathrm{c}}+q_{\mathrm{TT}}^{\mathrm{dis}}= \\ H_{\mathrm{Load}, t}+H_{\mathrm{LBR}, t} \end{gathered} $ | (19) |
| $ C_{\mathrm{LBR}, t}+C_{\mathrm{EC}, t}=C_{\mathrm{Load}, t} $ | (20) |
| $ G_{\mathrm{P} 2 \mathrm{H}, t}+v_{\mathrm{HT}}^{\mathrm{c}}+v_{\mathrm{HT}}^{\mathrm{dis}}=G_{\mathrm{Load}, t}+G_{\mathrm{FC}, t} $ | (21) |
式中: PWT, t、PPV, t、PFC, t——t时刻风机、光伏系统、燃料电池输出的电功率;
PLoad, t、HLoad, t、CLoad, t、GLoad, t——t时刻电、热、冷、氢负荷;
PEB, t、PEC, t、PP2H, t——t时刻电锅炉、电制冷机、电制氢装置输入的电功率;
HFC, t、HEB, t——t时刻燃料电池、电制热输出的热功率;
HLBR, t——t时刻溴化锂制冷机输入的热功率;
qTTc、qTTdis——t时刻储热罐充、放热功率;
CLBR, t、CEC, t——t时刻溴化锂制冷机、电制冷机输出的冷功率;
GP2H, t——t时刻电制氢装置产生的氢气;
vHTc、vHTdis——t时刻储氢罐充、放氢速率;
GFC, t——t时刻电制氢装置消耗的氢气。
3.2.3 设备出力约束
除了满足上述列出的功率平衡等式约束外, 系统内各设备的电、热和气出力也需满足其正常工作范围的上下限要求。
| $ P_{m, t, \min } \leqslant P_{m, t} \leqslant P_{m, t, \max } $ | (22) |
| $ H_{n, t, \min } \leqslant H_{n, t} \leqslant H_{n, t, \max } $ | (23) |
| $ C_{r, t, \min } \leqslant C_{r, t} \leqslant C_{r, t, \max } $ | (24) |
| $ G_{s, t, \min } \leqslant G_{s, t} \leqslant G_{s, t, \max } $ | (25) |
式中: Pm, t, min、Pm, t, max、Pm, t——任意m类电设备在t时刻正常运行时的最小、最大和实际发电功率;
Hn, t, min、Hn, t, max、Hn, t——任意n类热设备在t时刻正常运行时的最小、最大和实际发热功率;
Cr, t, min、Cr, t, max、Cr, t——任意r类冷设备在t时刻正常运行时的最小、最大和实际供冷功率;
Gs, t, min、Gs, t, max、Gs, t——电制氢设备在t时刻生产氢气的最小、最大和实际电功率。
3.2.4 储能设备约束
储能装置包括储氢罐、热储能装置, 应同时满足储能额定容量与交换功率约束。这里以储氢罐为例。
| $ \left\{\begin{array}{l} -\frac{\omega_{\mathrm{HT}} \Delta t}{\rho_{\mathrm{H}_2} \eta_{\mathrm{HT}}^{\mathrm{c}}} \leqslant v_{\mathrm{HT}}^{\mathrm{c}} \leqslant 0 \\ 0 \leqslant v_{\mathrm{HT}}^{\mathrm{dis}} \leqslant \frac{\omega_{\mathrm{HT}} \eta_{\mathrm{HT}}^{\mathrm{dis}} \Delta t}{\rho_{\mathrm{H}_2}} \\ S_{\mathrm{min}}^{\mathrm{G}} \leqslant S_t^{\mathrm{G}}=S_{t-1}^{\mathrm{G}}+\left[\frac{\eta_{\mathrm{HT}}^{\mathrm{c}} v_{\mathrm{HT}}^{\mathrm{c}} \rho_{\mathrm{H}_2}}{\omega_{\mathrm{HT}}} \mu_{\mathrm{HT}}+\right. \\ \left.\quad \frac{v_{\mathrm{HT}}^{\mathrm{dis}} \rho_{\mathrm{H}_2}}{\eta_{\mathrm{HT}}^{\mathrm{dis}} \omega_{\mathrm{HT}}}\left(1-\mu_{\mathrm{HT}}\right)\right] \Delta t \leqslant S_{\mathrm{max}}^{\mathrm{G}} \end{array}\right. $ | (26) |
式中: ωHT——储氢罐的配置容量;
ρH2——氢气密度;
ηHTc、ηHTdis——储氢罐充、放氢效率;
μHT——0, 1变量, 1为充氢状态, 0为放氢状态;
SmaxG、SminG——储氢罐的储能状态上、下限;
StG、St-1G——t时刻和t-1时刻储氢罐储存的氢气与容量的比值。
4 案例分析
4.1 算例数据与情景设置
为验证本文所提系统的合理性, 以某地区的实际算例为例, 进行仿真规划。该实际算例包括工业区、商业区、生活区3个园区。将原有的阶梯式碳交易模型和计及碳超额率的阶梯式碳交易模型分别设为模型1和模型2。模型1和模型2碳交易的基础价格、价格增长率均为200元/t, 0.25。模型1碳交易区间长度为165 t, 模型2碳交易区间长度为0.07。算例仿真在CPU为AMD Ryzen 5 5600H with Radeon Graphics的电脑上展开, 通过MATLAB R2017b软件编程实现。
针对本文构建的基于计及碳超额率的阶梯式碳交易的含电制氢综合能源系统规划模型, 均采用冷热电联供方式+电氢储能系统, 分以下6种情景讨论: 情景1, 工业区, 模型1;情景2, 工业区, 模型2;情景3, 商业区, 模型1;情景4, 商业区, 模型2;情景5, 生活区, 模型1;情景6, 生活区, 模型2。
4.2 优化配置结果分析
4.2.1 设备容量优化结果分析
不同情景下功能设备优化配置结果如表 1所示。
表 1
不同情景下功能设备优化配置结果
| 情景 | 总配置容量 | ||||||||||
| 风机 | 光伏系统 | 电锅炉 | 电制冷机 | 储热罐 | 微燃机 | 燃气轮机 | 溴化锂制冷机 | 电制氢装置 | 储氢罐 | 燃料电池 | |
| 情景1 | 5 553 | 7 069 | 5 156 | 694 | 306 | 3 188 | 2 476 | 1 000 | 931 | 1 849 | 244 |
| 情景2 | 5 874 | 7 048 | 5 189 | 686 | 361 | 3 808 | 2 511 | 992 | 988 | 1 849 | 282 |
| 情景3 | 4 994 | 1 738 | 1 175 | 366 | 1 037 | 853 | 1 171 | 450 | 1 726 | 1 678 | 1 871 |
| 情景4 | 4 928 | 4 200 | 1 977 | 342 | 351 | 1 655 | 793 | 384 | 942 | 1 201 | 585 |
| 情景5 | 2 517 | 1 765 | 789 | 184 | 1 500 | 641 | 1 425 | 228 | 1 881 | 1 900 | 436 |
| 情景6 | 2 953 | 1 983 | 903 | 215 | 390 | 736 | 1 096 | 109 | 1 793 | 1 846 | 1 604 |
由表 1可知, 相较于采用阶梯式碳交易模型1的情景1、3、5, 采用阶梯式碳交易模型2的情景2、4、6的电锅炉、电制冷机和燃气轮机的总配置容量相对较低, 其余风机、光伏系统、微燃机等设备的总配置容量相对较高。
4.2.2 不同阶梯式碳交易对规划方案的经济性影响分析
不同情景下经济性指标如表 2所示。
表 2
不同情景下经济性指标
| 情景 | 总成本 | 购电成本 | 购气成本 | 碳交易成本 | 投资成本 | 运维成本 |
| 情景1 | 1 440.46 | 86.34 | 143.21 | 3.53 | 1 137.49 | 69.89 |
| 情景2 | 1 438.98 | 76.39 | 121.58 | 2.87 | 1 167.49 | 70.65 |
| 情景3 | 901.03 | 93.20 | 71.18 | 5.29 | 718.18 | 13.18 |
| 情景4 | 899.66 | 69.62 | 88.34 | 2.08 | 726.73 | 12.89 |
| 情景5 | 559.43 | 32.12 | 46.33 | 3.81 | 464.63 | 15.54 |
| 情景6 | 603.29 | 16.38 | 31.19 | 0.66 | 487.07 | 15.99 |
由表 2可知: 对比情景1和情景2, 由于情景2中计及碳超额率的阶梯式碳交易促进风机和微燃机的容量上升, 因此情景2的投资和运维成本有所上升分别为1167.49万元和70.65万元, 但购电成本和购气成本以及碳交易成本均有所下降, 分别为76.39万元、121.58万元及2.87万元, 其中碳交易成本相当于降低了1%;对比情景3和情景4, 由于情景4中计及碳超额率的阶梯式碳交易促进光伏系统的容量和微燃机的容量上升, 因此情景4的投资成本有所上升为726.73万元, 但购电成本和碳交易成本有所降低, 分别为69.62万元和2.08万元, 其中碳交易成本相当于降低了60%;对比情景5和情景6, 由于情景6中计及碳超额率的阶梯式碳交易光伏系统和风机的容量有所上升, 情景6的投资成本和运维成本有所上升分别为487.07万元和15.99万元, 但购电成本、购气成本及碳交易成本有所降低, 分别为16.38万元、31.19万元与0.66万元, 其中碳交易成本下降了82%。综上所述, 计及碳超额率的阶梯式碳交易在促进新能源和微燃机的装机容量上有更好的效果, 增加的清洁能源满足了部分负荷需求, 导致综合能源系统向电网购买的电量也有所下降。对于规模越小的综合能源系统来说, 其碳交易金额下降的比例越大。对小规模的综合能源系统的减排有较好的激励作用。
4.2.3 不同阶梯式碳交易对规划方案的碳排放量影响分析
不同情景下碳排放指标如表 3所示。
表 3
不同情景下碳排放指标
| 情景 | 碳交易成本/元 | 碳排放量/t | 碳配额量/t | 碳超额量/t | 碳超额率 |
| 情景1 | 33 137 | 2 532.32 | 2 366.98 | 165.34 | 1.07 |
| 情景2 | 28 726 | 2 195.44 | 2 051.82 | 143.63 | 1.07 |
| 情景3 | 58 698 | 1 843.16 | 1 575.25 | 267.91 | 1.17 |
| 情景4 | 20 872 | 1 595.20 | 1 490.85 | 104.36 | 1.07 |
| 情景5 | 38 766 | 940.78 | 752.27 | 188.51 | 1.25 |
| 情景6 | 6 295 | 481.65 | 449.71 | 31.94 | 1.07 |
由表 3可知: 情景2的碳排放量相较于情景1降低了336.88 t, 即降低了13.3%, 碳超额率的变化并不是很大, 还是在同一个碳排放区间长度内; 情景4的碳排放量相较于情景3降低了247.96 t, 即降低了13.45%;情景6的碳排放量相较于情景5降低了459.13 t, 即降低了48.8%。
可见使用计及碳超额率的阶梯式碳交易模型能增加综合能源系统的减排能力, 并且综合能源系统的规模越小, 增加的减排能力越强。采用计及碳超额率的阶梯式碳交易机制使得3个园区的碳排放量总共降低1 043.97 t, 即降低了19.6%。
4.3 碳交易机制参数的影响
4.3.1 碳交易基础价格的影响
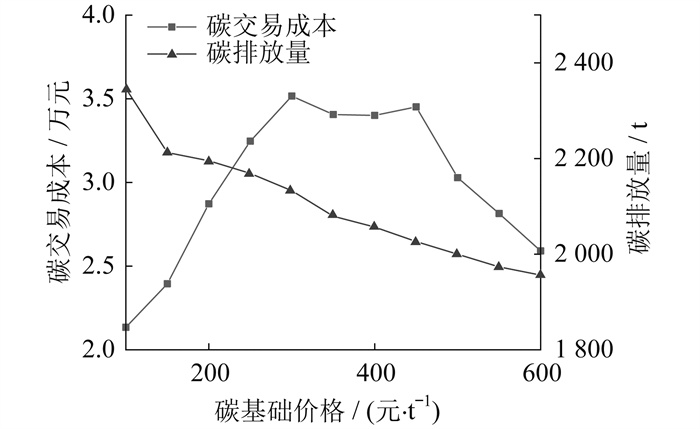
图 4展示了随着碳交易基础价格的变化, 情景2的碳交易成本和碳排放量的变化趋势。
由图 4可知: 情景2的碳排放量随着碳基础价格的上升而减少; 同时, 随着碳基础价格的上升, 情景2的碳交易成本皆呈现先上升后下降的趋势。
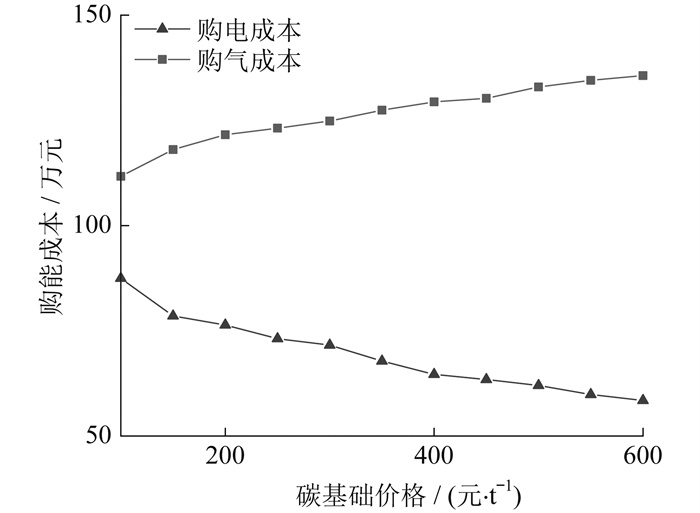
图 5展示了情景2下, 购电成本、购气成本随碳基础价格的变化趋势。
由图 5可知, 随着碳基础价格的升高, 情景2的购电成本下降, 购气成本上升。这是因为当碳基础价格升高时, 系统为了限制碳排放, 减少了对单位碳排放量相对较高的煤电的购买量, 增加对单位碳排量相对较低的天然气的购买量, 以提高微燃机和燃料电池的出力, 弥补减少的购电量。
综合上述分析可知, 含电制氢的综合能源系统的运行对碳基础价格的变动比较敏感, 整体呈现出随着碳交易价格的升高, 碳排放量下降、碳交易成本先升高后降低、能效增大的趋势。
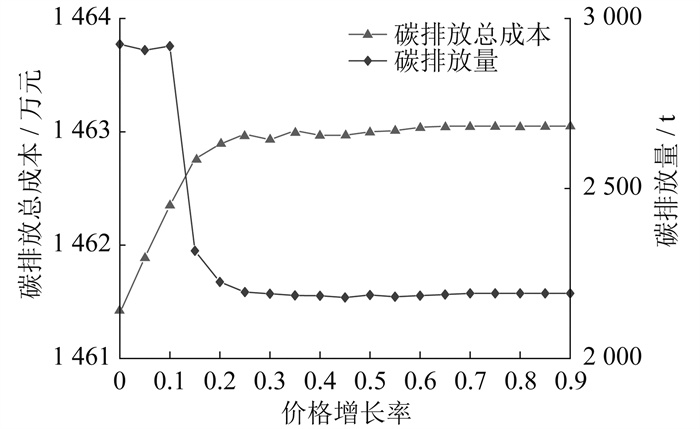
4.3.2 价格增长率的影响
4.3.3 碳交易区间参数的影响
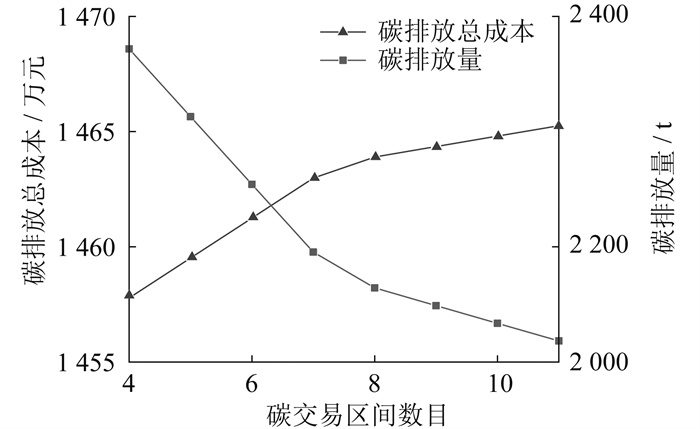
在计及碳超额率的阶梯式碳交易机制中, 由于碳超额率的最大值为1.48, 所以区间长度和区间数目可以一一对应。情景2下, 不同碳交易区间数目的碳排放总成本和碳排放量的变化趋势如图 7所示。
由图 8可知: 当碳交易区间数目在[0, 7)时, 随着碳交易区间数目的增加, 碳排放量急剧下降; 当区间数目增加到7时, 碳排放总成本和碳排放量出现较明显的拐点, 即改变区间长度对计及碳超额率的阶梯式碳交易机制的影响开始减弱, 但此时计及碳超额率的阶梯式碳交易机制也能有较好的碳约束能力。
5 结语
本文建立了计及碳超额率的阶梯式碳交易的含电制氢综合能源系统规划模型, 以电、氢、冷、热4种能量平衡和元器件工作特性为约束, 采用非支配性算法和商用求解器结合的混合智能算法进行求解, 得到系统各设备的最优容量配置。计及碳超额率的阶梯式碳交易机制, 对碳排放量的控制更严格, 使系统优化规划更偏向低碳设备; 系统的碳排放指标对计及碳超额率的阶梯式交易机制的参数, 即碳基础价格、价格增长率、碳交易区间长度的变化较敏感。后续工作可进一步围绕计及碳超额率的阶梯式碳交易机制在多园区综合能源系统联合规划中的应用。
参考文献
-
[1]顾欣, 王琦, 胡云龙, 等. 基于纳什议价的多微网综合能源系统分布式低碳优化运行策略[J]. 电网技术, 2022, 46(4): 1464-1482.
-
[2]ASL D K, SEIFI A R, RASTEGAR M, et al. Multi-objective optimal operation of integrated thermal-natural gas-electrical energy distribution systems[J]. Applied Thermal Engineering, 2020, 181: 115951. DOI:10.1016/j.applthermaleng.2020.115951
-
[3]ZENG C Y, JIANG Y C, LIU Y Q, et al. Optimal dispatch of integrated energy system considering energy hub technology and multi-agent interest balance[J]. Energies, 2019, 12(16): 3112. DOI:10.3390/en12163112
-
[4]YU Y, CHEN H, CHEN L, et al. Optimal operation of the combined heat and power system equipped with power-to-heat devices for the improvement of wind energy utilization[J]. Energy Science & Engineering, 2019, 7(5): 1605-1620.
-
[5]李健强, 余光正, 汤波, 等. 考虑风光利用率和含氢能流的多能流综合能源系统规划[J]. 电力系统保护与控制, 2021, 49(14): 11-20.
-
[6]任洲洋, 罗潇, 覃惠玲, 等. 考虑储氢物理特性的含氢区域综合能源系统中长期优化运行[J]. 电网技术, 2022, 46(9): 3324-3333.
-
[7]邓杰, 姜飞, 王文烨, 等. 考虑电热柔性负荷与氢能精细化建模的综合能源系统低碳运行[J]. 电网技术, 2022, 46(5): 1692-1704.
-
[8]张景淳, 陈胜, 彭琰, 等. 计及灵活爬坡的气-电耦合综合能源系统低碳经济调度研究[J]. 电网技术, 2022, 46(9): 3315-3325.
-
[9]杨龙, 张沈习, 程浩忠, 等. 区域低碳综合能源系统规划关键技术与挑战[J]. 电网技术, 2022, 46(9): 3290-3304.
-
[10]胡静哲, 王旭, 蒋传文, 等. 计及综合能源服务商参与的电力系统低碳经济调度[J]. 电网技术, 2020, 44(2): 514-522.
-
[11]陈志, 胡志坚, 翁菖宏, 等. 基于阶梯碳交易机制的园区综合能源系统多阶段规划[J]. 电力自动化设备, 2021, 41(9): 148-155.
-
[12]矫舒美, 乔学博, 李勇, 等. 计及综合能源系统全寿命周期碳排放和碳交易的电转气设备和光伏联合优化配置[J]. 电力自动化设备, 2021, 41(9): 156-163.