|
|
|
发布时间: 2023-12-28 |
综合能源 |
|
|
|
收稿日期: 2023-07-10
中图法分类号: TM715
文献标识码: A
文章编号: 2096-8299(2023)06-0557-06
|
摘要
在保障风光氢储综合供电系统可靠性的前提下,为最大限度地降低单位发电成本,提升系统整体的经济性,提出了一种引入自立策略的改进麻雀搜索算法(SSA),并根据该方法对风光氢储综合供电系统电源容量配置进行了优化。建立以最小化单位发电成本为目标函数的优化模型,采用改进SSA算法进行求解。研究结果显示:该算法具有较好的寻优能力,系统单位发电成本降低了23.3%。
关键词
风力发电; 光伏发电; 氢储能; 容量优化配置; 改进麻雀搜索算法
Abstract
On the premise of ensuring the reliability of the wind solar-hydrogen-storage integrated power supply system, in order to minimize the unit power generation cost and improve the overall economy of the system, a sparrow search algorithm based on self-reliance strategy is proposed, and the power capacity configuration of the wind-solar-hydrogen storage integrated power supply system is optimized based on this method.An optimization model is established that minimizes the unit power generation cost as the objective function, and an improved algorithm is used to solve it.The results show that the algorithm has good optimization ability, reducing the unit power generation cost of the system by 23.5%.
Key words
wind power generation; photovoltaic power generation; hydrogen energy storage; capacity optimization configuration; improved sparrow search algorithm
2021年12月, 工业和信息化部发布的《“十四五”工业绿色发展规划》明确了“十四五”时期我国可再生能源行业, 包括太阳能、风能、储能和氢能产业发展的实施路径。可以预见, 太阳能、风能、储能和氢能在“十四五”期间将迎来利好发展。微电网是集发电、储能、负荷等功能于一身的小型电力系统[1]。风光氢储综合供电系统是一种典型的微电网, 采用可再生能源制氢, 然后通过氢
系统储能, 可跨时空平抑新型电力系统的波动性, 具有功能独特的优势, 成为微电网领域的研究热点之一[2]。容量优化配置是微电网系统优化设计的重要内容之一, 也是保障系统稳定运行的重要基础[3]。但微电网系统中分布式电源种类较多且各发电单元出力特性差异较大, 因而容量优化配置呈现高度非线性、复杂性和不确定性, 使用传统的纯数学优化方法不仅计算量大、时间长而且难以取得令人满意的结果[4]。
近年来, 以粒子群算法(Particle Swarm Optimization, PSO)[5]为代表的群智能算法在容量优化配置方面取得了较好的成果。SUHANE P等人[6]以负荷需求的连续性和负荷缺电率为目标函数建立了优化模型, 采用蚁群算法(Ant Colony Optimization, ACO)求解得出结果。WANG Z K等人[7]以系统的年平均成本为优化目标, 在保证供电可靠性的前提下, 采用一种改进遗传算法(Improved Genetic Algorithm, IGA)进行算例求解分析。HOU H等人[8]提出一种风光重力储能的综合发电系统, 以系统总投资最低作为目标函数, 采用猫群算法(Cat Swarm Optimization, CSO)求解。但是, 目前提到的群智能算法, 均存在全局搜索能力差、寻优精度不足、参数设置复杂及收敛速度慢等问题, 导致其在实际应用中仍有不足。
麻雀搜索算法(Sparrow Search Algorithm, SSA)是一种新颖的群智能算法, 其参数设置简单, 寻优精度更高、收敛速度更快[9]。DONG J等人[10]采用SSA优化微电网容量配置, 并证明其计算时间与寻优能力均十分优秀。但SSA仍然存在搜索后期收敛速度较慢, 以及全局搜索能力下降的问题。为此, 本文在分析系统各设备出力模型的基础上, 建立以最小化单位发电成本为目标函数的容量配置模型, 并利用一种引入自立策略(Zili Strategy)的改进SSA算法模型对算例求解, 通过算例分析验证优化模型的准确性, 并评价最优配置方案下系统的经济性。
1 风光氢储综合供电系统结构及各设备出力模型
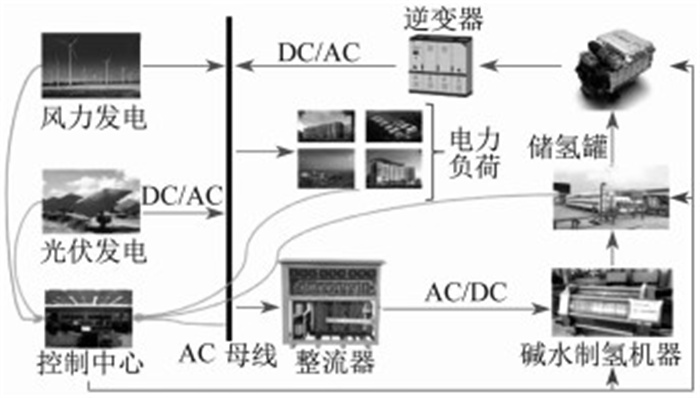
1.1 风光氢储综合供电系统结构
风光氢储综合供电系统结构如图 1所示。
1.2 光伏发电出力模型
光伏组件实际输出功率可由光照强度、环境温度以及标准条件下额定功率确定。具体表示为
| $ P_{\mathrm{PV}}(t)=P_{\mathrm{stc}} \frac{G(t)}{G_{\mathrm{stc}}}\left\{1-\beta_0\left[T_{\mathrm{cell}}(t)-25\right]\right\} $ | (1) |
式中: PPV(t)——t时刻的光伏出力, kW;
Pstc——光伏电池在标准测试条件下(25.0 ℃, 1.0 MPa)的最大输出功率, kW;
G(t)——t时刻辐照度, W/m2;
Gstc——标准测试条件下的辐照度, 取1 000 W/m2;
β0——温度系数, 取0.4%/℃;
Tcell(t)——t时刻的光伏组件温度, ℃。
1.3 风力发电出力模型
风力发电机组的出力主要与风速有关。其功率模型为
| $ P_{\mathrm{wT}}=C_{\mathrm{p}} P_{\mathrm{w}}=\frac{1}{2} \rho C_{\mathrm{p}} S v^3 $ | (2) |
式中: PWT——风力发电机出力, kW;
Cp——风能利用系数;
Pw——风功率, kW;
ρ——空气密度, kg/m3;
S——风流过的有效截面积, m2;
v——风速, m/s。
1.4 燃料电池出力模型
为更快速地响应负荷需求变化, 采用效率较高且启停速度较快的质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)。其耗氢量为
| $ M_{\mathrm{H}_2}=m_{\mathrm{H}_2} \frac{n I}{2 F} $ | (3) |
式中: MH2——耗氢量, mol;
mH2——氢的摩尔质量, 2 g/mol;
n——燃料电池单元数, 个;
I——输出电流, A;
F——法拉第常数, 取96 485.33 C/mol。
输出功率公式为
| $ P_{\mathrm{fc}}(t)=U_{\mathrm{fc}} I $ | (4) |
式中: Pfc(t)——t时刻的输出功率, kW;
Ufc——输出电压, V。
1.5 碱性电解槽模型
碱性电解槽是目前性价比最高的电解槽, 工作时氢气产生的速率与电解电路当中电流的大小相关, 计算公式为
| $ n_{\mathrm{el}}=\frac{\eta_{\mathrm{F}} n_{\mathrm{c}} I_{\mathrm{el}}}{2 F} $ | (5) |
| $ \eta_{\mathrm{F}}=96.5 \exp \left(\frac{0.09}{I_{\mathrm{el}}}-\frac{75.5}{I_{\mathrm{el}}^2}\right) $ | (6) |
式中: nel——产氢速率;
ηF——法拉第效率;
nc——电解槽串联数, 个;
Iel——电解槽电流, A。
2 风光氢储综合供电系统容量配置优化模型
2.1 目标函数
系统优化变量定义为
| $ \boldsymbol{N}=\left[\begin{array}{lllll} N_1 & N_2 & N_3 & N_4 & N_5 \end{array}\right] $ | (7) |
式中: Ni——系统中第i种设备(风力发电机、光伏板、PEMFC、碱性电解槽和储氢罐)的数目, i=1, 2, 3, 4, 5。
风光氢储容量配置的主要优化目标是在保障供电可靠性的前提下, 最小化单位发电成本, 最大化碳交易收益。具体目标函数为
| $ f(X)=C_{\text {generation }}+C_{\text {reliability }} $ | (8) |
式中: Cgeneration——系统单位发电成本, 元/kWh;
Creliability——可靠性成本, 元。
系统单位发电成本是系统总投资成本与发电量的比值, 表征整个系统经济性的优劣。其计算公式为
| $ C_{\text {generation }}=\frac{C_{\text {total }}}{P_{\text {total }}} $ | (9) |
| $ C_{\text {total }}=C_{\mathrm{g}}+C_{\mathrm{w}}+C_{\mathrm{h}} $ | (10) |
式中: Ctotal——系统寿命周期内总投资成本, 元;
Ptotal——系统寿命周期内总发电量, kWh;
Cg——各设备的初始购入成本, 元;
Cw——各设备的运行和维护成本, 元;
Ch——各设备的置换成本, 元。
为凸显系统供电可靠性, 故将可靠性指标以惩罚函数的形式引入到目标函数式(8)当中, 即
| $ f(X)=C_{\text {generation }}+C_{\text {reliability }}+C_{\mathrm{r}} $ | (11) |
| $ C_{\mathrm{r}}=\left\{\begin{array}{l} 0, \quad P_{\mathrm{LPS}} \leqslant 0.01 \\ 1.0 \times 10^9, \quad P_{\mathrm{LPS}}>0.01 \end{array}\right. $ | (12) |
| $ P_{\text {LPS }}=\frac{N_{P_{\mathrm{net}}(t)<0}}{8760} $ | (13) |
| $ P_{\text {net }}(t)=\sum\limits_{i=1}^3 P_i(t)-P_{\text {load }}(t) $ | (14) |
式中: PLPS——系统负荷缺电率, 是一年中系统不能满足电网负荷需求的小时数;
NPnet(t)<0——系统在一年中净功率小于零的小时数;
Pnet(t)——系统在t时刻的净功率, kW;
Pi(t)——第i种设备t时刻的功率, kW;
Pload(t)——在t时刻负荷所需求的功率, kW。
2.2 约束条件
(1) 功率平衡约束 功率约束方面, 首先整个系统无论何时都需要满足功率平衡约束, 即单位时间内系统中所有发电设备的出力要能够满足负荷需求。
| $ \sum\limits_{i=1}^3 N_i \cdot P_i(t)=P_{\text {load }}(t) $ | (15) |
(2) 输出功率约束 实际工程应用当中, 无论何种发电设备, 在安装时都需要满足一定的容量上限。
| $ S_i=\sum\limits_{j=1}^{N_i} N_{i j} \cdot P_i \leqslant S_{i \max } \quad i=1, 2, 3 $ | (16) |
式中: Si——第i种设备的总装机容量, kW;
Nij——第i种设备中的第j个单元的数目;
Pi——第i种设备的额定功率, kW;
Simax——第i种设备的最大装机容量, kW。
3 算法介绍
3.1 SSA算法
采用SSA求解时, 麻雀种群的位置, 也就是潜在的解, 可以表示为
| $ \boldsymbol{X}=\left[\begin{array}{cccc} X_{1, 1} & X_{1, 2} & \cdots & X_{1, d} \\ X_{2, 1} & X_{2, 2} & \cdots & X_{2, d} \\ \vdots & \vdots & & \vdots \\ X_{c, 1} & X_{c, 2} & \cdots & X_{c, d} \end{array}\right] $ | (17) |
式中: c——麻雀的个数;
d——问题的维数;
Xm, n——第m只麻雀在第n维的坐标值。
这样, 所有麻雀的适应度值就可以表示
| $ \boldsymbol{F}_{x}=\left[\begin{array}{cccc} f(X_{1, 1} & X_{1, 2} & \cdots & X_{1, d}) \\ f(X_{2, 1} & X_{2, 2} & \cdots & X_{2, d}) \\ \vdots & \vdots & & \vdots \\ f(X_{c, 1} & X_{c, 2} & \cdots & X_{c, d}) \end{array}\right] $ | (18) |
式(18)的矩阵当中, 每一行都代表一只麻雀个体的适应度值。
生产者需要为整个种群尽可能多地寻找好的食源位置, 因此生产者的位置更新公式为
| $ X_{m, n}^{k+1}=\left\{\begin{array}{l} X_{m, n}^k \cdot \exp \left(\frac{-m}{\alpha k_{\max }}\right), \quad R_2<S_{\mathrm{T}} \\ X_{m, n}^k+Q, \quad R_2 \geqslant S_{\mathrm{T}} \end{array}\right. $ | (19) |
式中: k——当前迭代次数;
Xm, nk——第m只麻雀在迭代k次时第n维位置的值;
α——[0, 1]上的随机数;
kmax——最大迭代次数;
R2——警报值, 取值范围为[0, 1];
ST——安全阈值, 取值范围为[0.5, 1];
Q——服从正态分布的随机数。
当R2<ST时, 表示周围没有捕食者, 生产者采用宽搜索模式; 反之, 表示已有个体发现了捕食者并且发出警报, 为躲避追捕, 麻雀需要迅速飞到安全地区。
跟随者的位置更新公式为
| $ X_{m, n}^{k+1}=\left\{\begin{array}{l} Q \cdot \exp \left(\frac{X_{\mathrm{w}(1, n)}^k-X_{m, n}^k}{m^2}\right), \quad m>\frac{c}{2} \\ X_{p(1, n)}^{k+1}+\left|X_{m, n}^k-X_{p(1, n)}^{k+1}\right| \cdot A_{(1, n)}^{+}, \quad \text { 其他 } \end{array}\right. $ | (20) |
式中: Xp(1, n)k+1——第k+1次迭代时具有最优适应值位置矢量第1行第n列的值;
Xw(1, n)k——第k次迭代时全局最劣位置矢量第1行第n列的值;
A(1, n)+——矩阵 A+第1行第n列的值, A为1×d阶的矩阵, 其中各元素随机为-1或1, A+= AT(AAT)-1。
式(20)中, m>c/2的跟随者可能会因无法获得食物而挨饿。
3.2 改进SSA算法
从式(20)可知, 当生产者具有较好的适应值位置时, 跟随者会趋向于集中在这些发现者周围, 因此降低了跟随者出现在其他位置的概率, 削弱了算法后期的全局搜索能力。为打破这种过分聚集的现象, 可发动在种群数量居多的跟随者来解决这一问题, 于是引入自立策略来改进算法。
体现在算法中, 表述为m>c/2的跟随者个体会以一定的概率, 随机地以生产者的位置信息或者其他有可能会有食物的位置信息来更新自己的当前位置。这就是自立策略。
对于m>c/2的跟随者, 先在种群当中随机选取两个不同的个体, 二者做差如下:
| $ \boldsymbol{Z}^k=\boldsymbol{X}_{l 1}^k-\boldsymbol{X}_{l 2}^k $ | (21) |
式中: Zk——二者做差后得到的随机矢量;
Xl1k、Xl2k——种群中索引号为l1、l2的随机个体的位置。
将得到的随机矢量赋予相应权重加到另一个随机个体的位置矢量当中就得到了自立策略的随机搜索位置。其表达式如下:
| $ \boldsymbol{W}^{k+1}=\boldsymbol{X}_{l 3}^k+\boldsymbol{f} \cdot \boldsymbol{Z}^k $ | (22) |
式中: Wk+1——随机搜索位置矢量;
Xl3k——索引号为l3的第3个随机的个体位置矢量;
f——权重因子, 取值范围为[0, 2]。
根据得到的随机搜索位置和当前迭代次数下的全局最优位置, 式(20)可更新为
| $ L_{m, n}^{k+1}=\left\{\begin{array}{l} W_{m, n}^{k+1}, m>\frac{c}{2} \text { 且 } r_{\mathrm{and}} \leqslant Z_{\mathrm{L}} \\ X_{p(1, n)}^{k+1}+r_{\text {and }}\left(X_{p(1, n)}^{k+1}-X_{m, n}^k\right), m>\frac{c}{2} \text { 且 } r_{\text {and }}>Z_{\mathrm{L}} \\ X_{p(1, n)}^{k+1}+\left|X_{m, n}^k-X_{p(1, n)}^{k+1}\right| \cdot \boldsymbol{A}_{(1, n)}^{+}, \text {其他 } \end{array}\right. $ | (23) |
式中: Lm, nk+1——基于自立策略的自立位置矢量的第m行第n列的值;
Wm, nk+1——随机搜集位置矢量的第m行第n列的值;
rand——[0, 1]的随机数;
ZL——自立概率, [0, 1], 用于决定自立位置各个维度的具体数据由随机搜索位置还是全局最优解来提供。
改进SSA算法迭代后, 其依靠随机改变跟随者位置更新方式, 更能够提升其跳出局部最优解的能力, 因此自立策略改进后的SSA算法能够在充分利用全局最优解的同时, 做到不过分依赖全局最优解来克服后期全局搜索能力不足的困难。
4 算例分析
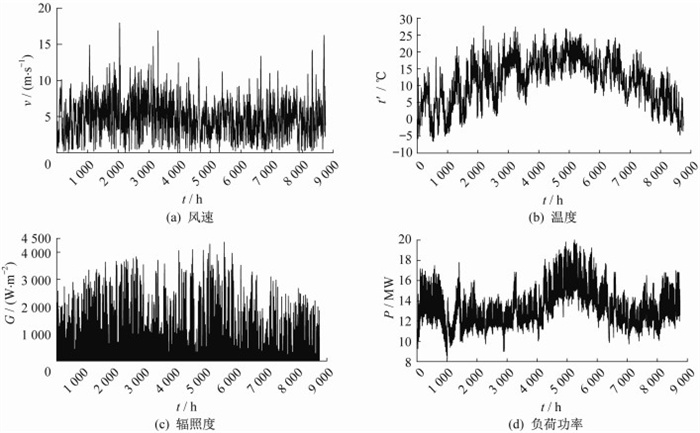
4.1 风光资源及负荷数据
图 2给出了贵州省威宁地区2021全年的风速v、温度t′、辐照度G和负荷功率P曲线。
4.2 设备参数选择和参数设置
4.3 计算求解
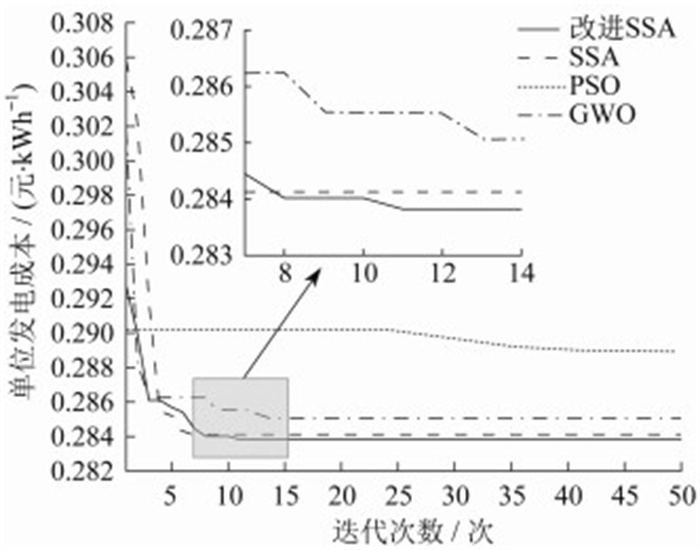
根据前文所述的基本信息, 在MATLAB当中编写目标函数信息后进行求解, 将PSO、SSA、改进SSA、GWO算法[11]运行结果进行对比。PSO算法中, 最大速度vmax设置为6, 学习因子c1、c2设置为2;SSA算法和改进SSA算法中的预警值均设置为0.8, 生产者比例为20%, 自立概率ZL为0.5;GWO算法中参数无需人为设定。各算法的迭代求解过程如图 3所示。
由图 3可知, 改进SSA算法在迭代11次时收敛, 而SSA算法在迭代7次时收敛, 二者在计算速度方面相差不大, 但从结果来看, 改进SSA跳出局部最优解的能力较SSA算法有了一定的提升, 改进SSA算法在迭代第8次时, 有了较好的全局最优解0.2841后, 仍然继续寻优得出了最终的全局最优解, 体现了自立策略对于提升跳出局部最优的作用。各算法目标函数最优值f(X)如表 2所示。
表 2
各算法目标函数最优值
| 算法 | N1 | N2 | N3 | N4 | N5 | f(X) |
| 改进SSA | 109 | 20 019 | 442 | 537 | 2 | 0.283 7 |
| SSA | 121 | 20 001 | 445 | 553 | 2 | 0.284 1 |
| PSO | 374 | 20 005 | 464 | 577 | 5 | 0.289 0 |
| GWO | 119 | 20 019 | 450 | 577 | 4 | 0.285 0 |
由表 2可知, 改进SSA算法求得的目标函数最优值为0.283 7, 优于PSO、GWO的求解结果, 略优于SSA的求解结果, 再次说明了改进SSA算法的全局寻优能力以及寻优精度都有了一定的提升。
从结果层面来看, 目标函数最优值为0.283 7元/kWh, 也就是说整个系统每发1 kWh的成本约是0.283 7元, 而按照单纯的光伏电站或风电站的成本电价为0.37元/kWh来计算, 单位发电成本降低了23.3%。
在最优配置的情况下, 结合全年的风速、温度和辐照度数据, 可以得出风能和光伏的全年发电量约为1.2亿kWh。该微电网系统相比于单纯的光伏或者风电站每年可多获利约1 036万元, 按照运行年限为20 a来计算, 在整个寿命周期内一共可以多盈利2.07亿元, 收益提升十分可观。
5 结语
本文提出了一种基于氢储能的微电网系统, 建立了以系统单位发电成本为优化目标, 各主要设备的数量为自变量的目标函数, 综合考虑了系统层面的可靠性约束条件以及各设备自身的功率约束条件, 并采用一种改进SSA算法求解。研究结果显示, 优化配置后, 整个风光氢储综合供电系统的单位发电成本相比于传统化石燃料发电降低23.3%, 且这种风光氢储综合供电系统碳排放几乎为零。因此, 建设此类供电系统对于我国“3060”电力转型具有重要意义。
自立策略有效地改善了SSA算法迭代后期全局搜索能力下降的缺点, 因而改进SSA算法具有更高全局寻优精度, 对于解决微电网容量配置问题及其他具有非线性目标函数的规划类问题具有一定的推广应用价值。
参考文献
-
[1]ESO N G. Technical report on the events of 9 august 2019[R]. Warwick, UK: National Grid ESO, 2019.
-
[2]MALEKI A. Design and optimization of autonomous solar-wind-reverse osmosis desalination systems coupling battery and hydrogen energy storage by an improved bee algorithm[J]. Desalination, 2018, 435: 221-234. DOI:10.1016/j.desal.2017.05.034
-
[3]AI-FALAHI M D A, JAYASUBGHE S D G, ENSHAEI H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system[J]. Energy Conversion and Management, 2017, 143: 252-274. DOI:10.1016/j.enconman.2017.04.019
-
[4]RAJANNA S, SAINI R P. Development of optimal integrated renewable energy model with battery storage for a remote Indian area[J]. Energy, 2016, 111: 803-817. DOI:10.1016/j.energy.2016.06.005
-
[5]SUN C T, ZHANG C X, ZHOU S R. Simulation of composite energy storage optimization configuration of micro-grid based on PSO[J]. IOP Conference Series: Materials Science and Engineering, 2019, 677(4): 042103. DOI:10.1088/1757-899X/677/4/042103
-
[6]SUHANE P, RANGNEKAR S, MITTAL A, et al. Sizing and performance analysis of standalone wind-photovoltaic based hybrid energy system using ant colony optimisation[J]. IET Renewable Power Generation, 2016, 10(7): 964-972. DOI:10.1049/iet-rpg.2015.0394
-
[7]WANG Z K, JIA Y, CAI C, et al. Study on the optimal configuration of a wind-solar-battery-fuel cell system based on a regional power supply[J]. IEEE Access, 2021, 9: 47056-47068. DOI:10.1109/ACCESS.2021.3064888
-
[8]HOU H, XU T, WU X, et al. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system[J]. Applied Energy, 2020, 271: 115052. DOI:10.1016/j.apenergy.2020.115052
-
[9]XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
-
[10]DONG J, DOU Z, SI S, et al. Optimization of capacity configuration of wind-solar-diesel-storage using improved sparrow search algorithm[J]. Journal of Electrical Engineering & Technology, 2022, 17: 1-14.
-
[11]MIRJALILI S, MIRJALILI S M, LEWIA A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61.