|
|
|
发布时间: 2023-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-07-06
中图法分类号: TM77
文献标识码: A
文章编号: 2096-8299(2023)06-0549-08
|
摘要
提出了一种多社区分布式储能双层共享运行策略。首先,阐述了分布式储能的双层共享模式,包括上层用户侧储能共享和下层社区间储能共享。其次,基于广义纳什议价理论建立了多社区合作运行模型,并将该合作模型分解为合作联盟成本最小化与合作联盟收益分配。然后,利用改进交替方向乘子法求解合作联盟成本最小化问题,并基于广义纳什议价理论计算各参与者的贡献度,求解合作联盟的收益分配问题。最后,通过算例分析证明了所提出模型的有效性和实用性。
关键词
分布式储能; 广义纳什议价理论; 共享运行优化
Abstract
A multi-community distributed energy storage sharing strategy is proposed.Firstly, it elucidates the dual-sharing mode of distributed energy storage, comprising upper-level user-side energy storage sharing and lower-level inter-community energy storage sharing.Next, based on the generalized Nash bargaining theory, a multi-community cooperative operation model is established, which is further decomposed into subproblems of minimizing community cooperative alliance costs and allocating cooperative profits.Subsequently, an improved alternating direction multiplier is employed to solve the cooperative alliance cost minimization subproblem, and the cooperative contributions of each participant are calculated using the generalized Nash bargaining theory as the benchmark to solve the cooperative alliance profit allocation subproblem.Finally, through case studies, the effectiveness and practicality of the proposed model are demonstrated.
Key words
distributed energy storage; generalized Nash bargaining theory; sharing operation optimization
当今世界面临着全球气候变化、能源短缺、能源安全等诸多挑战, 储能技术逐渐成为解决能源转型和提高能源利用效率的重要手段。在分布式能源系统中, 分布式储能技术作为一种关键技术, 可以提高能源利用效率, 并降低能源消耗。
目前已有较多文献对储能共享问题展开了研究。文献[1-2]探讨了在未来电力系统中实现储能共享的“云”形态, 并对该形态下的商业模式进行了详细分析。文献[3-7]研究了基于P2P技术的储能共享模式, 在该模式下用户可以直接将自己的储能资源出租给其他用户, P2P技术可以确保交易的透明性和安全性, 激励用户积极参与共享。
在储能共享过程中, 合作后的收益分配问题也是研究的重点内容, 其中较为常用的方法是纳什议价理论。文献[8]提出了一种基于标准纳什谈判模型的合作博弈策略, 解决了新能源发电主体与电制氢主体之间的博弈问题, 实现了帕累托最优的整体效益。文献[9]提出了一种基于进化博弈论的纳什议价方法, 解决了配电网中各大工业用户间共享储能系统的交易定价问题。文献[10-12]均采用了一般的纳什议价模型, 其假设参与者在协商中获得的利益增幅相同, 就可能使得合作中作出不同贡献的参与者感到不公平。广义纳什议价理论[13-15]引入了一个非对称的议价能力参数, 与各参与者的贡献程度正相关, 考虑到了多参与者进行议价的情况, 每个参与者的议价能力参数不是客观不变的, 而是根据各用户策略相应改变的, 所以这种方法能够更公平地分配合作后的利益。
本文提出了一种多社区分布式储能双层共享运行策略, 基于广义纳什议价理论建立了多社区合作运行模型, 通过分时共享分布式储能, 实现用户之间储能资源的优化利用, 提高产消者的综合收益。通过算例分析验证了所提策略的有效性和实用性, 为分布式储能资源的高效利用提供了一种新的解决方案。
1 分布式储能双层共享模式
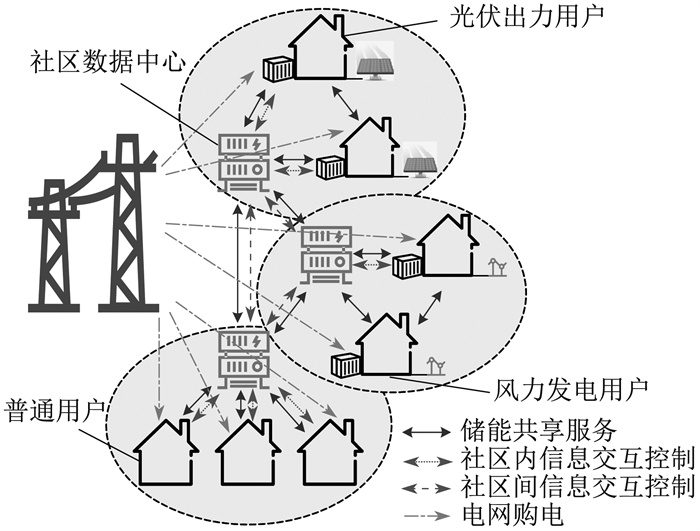
基于社区联盟的分布式储能双层P2P共享模式可以整合邻近多社区储能资源, 降低整体用能成本。该共享模式的示意图如图 1所示。
本文提出的分布式储能双层共享模式可分为以下4个步骤。
步骤1 用户将自己的储能资源接入社区分布式储能管理系统中, 各用户制定自身储能容量共享计划, 即具体的储能使用容量与可提供共享的储能容量;
步骤2 用户之间对各自储能容量共享计划进行信息交互和相互协调, 以确定最终的储能容量共享计划;
步骤3 社区内部参与储能共享的用户自发组成联盟, 以社区数据中心为中介整合社区内部通信数据, 并代表本社区与其他社区进行信息交互和相互协调;
步骤4 相邻社区之间存在一定的连接基础设施用于进行社区间的储能共享, 社区之间利用区块链技术进行共享交易, 并且各参与用户利用智能手机等终端设备对自身分配到的储能资源进行调用, 在交易过程中确保交易的透明性和安全性。
步骤1与步骤2为上层社区内部用户之间的储能共享, 步骤3为下层社区之间的储能共享, 步骤4为合作后的资源配置。社区数据中心为该社区分布式储能管理系统的智能数据中心。
2 合作模型的建立
2.1 用户模型
2.1.1 用户用能成本
参与储能共享的各用户用能成本公式为
| $ C_{j, i, \text { user }}=\sum\limits_{t \in T}\left(\lambda_t^{\text {buy }} P_{j, i, t}^{\text {buy }}-\lambda_t^{\text {ses }} P_{j, i, t}^{\text {ses }}+C_{j, i, t}^{\text {carbon }}\right) $ | (1) |
式中: Cj, i, user——j社区i用户的用能成本;
T——一日内的总时间段, 取为24;
λtbuy、λtses——t时刻j社区i用户的购电价格、售电价格;
Pj, i, tbuy、Pj, i, tses——t时刻j社区i用户的购电功率、售电功率;
Cj, i, tcarbon——t时刻j社区i用户的碳排放成本。
社区的CO2排放量主要来源于电网购电, 用户的碳排放成本计算公式为
| $ C_{j, i, t}^{\text {carbon }}=\beta c^{\text {carbon }} P_{j, i, t}^{\text {buy }} $ | (2) |
式中: β——碳排放因子;
ccarbon——碳价。
2.1.2 用户约束条件
分布式储能运行约束条件为
| $ E_{j, i}^t=E_{j, i}^{t-1}+\eta_{j, i}^{\mathrm{ch}} P_{j, i, t}^{\mathrm{ch}} \Delta t-\frac{P_{j, i, t}^{\mathrm{dis}} \Delta t}{\eta_{j, i}^{\mathrm{dis}}} $ | (3) |
| $ E_{j, i}^0=E_{j, i}^{24} $ | (4) |
| $ 0 \leqslant E_{j, i}^t \leqslant E_{j, i, \max } $ | (5) |
| $ 0 \leqslant P_{j, i, t}^{\mathrm{ch}} \leqslant \varepsilon_{j, i, t}^{\mathrm{ch}} P_{j, i, \max } $ | (6) |
| $ 0 \leqslant P_{j, i, t}^{\mathrm{dis}} \leqslant \varepsilon_{j, i, t}^{\mathrm{dis}} P_{j, i, \max } $ | (7) |
| $ \varepsilon_{j, i, t}^{\mathrm{ch}}+\varepsilon_{j, i, t}^{\text {dis }} \leqslant 1 $ | (8) |
| $ P_{j, i, \max }=\mu E_{j, i, \max } $ | (9) |
式中: Ej, it、Ej, it-1——t时刻和t-1时刻j社区i用户储能装置的存储电量;
ηj, ich、ηj, idis——j社区i用户的充电效率和放电效率;
Pj, i, tch、Pj, i, tdis——t时刻j社区i用户的充电功率、放电功率;
Δt——优化过程的最小时间段, 为1 h;
Ej, i0、Ej, i24——j社区i用户储能装置的初始电量和终止电量;
Ej, i, max——j社区i用户储能装置的最大存储电量;
εj, i, tch、εj, i, tdis——t时刻j社区i用户的充电状态变量和放电状态变量, 为布尔型变量, 用以保证用户的储能装置不会同时充放电;
Pj, i, max——j社区i用户储能装置的最大充放电功率;
μ——储能装置的能量倍率。
可再生能源出力约束条件为
| $ 0 \leqslant P_{j, i, t}^{\mathrm{PV}} \leqslant P_{j, i, \max }^{\mathrm{PV}} $ | (10) |
| $ 0 \leqslant P_{j, i, t}^{\mathrm{WT}} \leqslant P_{j, i, \text { max }}^{\mathrm{WT}} $ | (11) |
式中: Pj, i, tPV——t时刻j社区i用户的光伏出力;
Pj, i, maxPV——j社区i用户的光伏最大出力;
Pj, i, tWT——t时刻j社区i用户的风力发电出力;
Pj, i, maxWT——j社区i用户的风力发电最大出力。
功率平衡约束条件为
| $ L_{j, i, t}-P_{j, i, t}^{\mathrm{PV}}-P_{j, i, t}^{\mathrm{WT}}=P_{j, i, t}^{\mathrm{buy}}-P_{j, i, t}^{\mathrm{ses}}-P_{j, i, t}^{\mathrm{ch}}+P_{j, i, t}^{\mathrm{dis}} $ | (12) |
式中: Lj, i, t——t时刻j社区i用户的用电需求功率。
2.2 社区整体模型
2.2.1 多社区储能运行成本
充放电操作带来的分布式储能的退化成本是不可忽略的非线性成本。结合文献[16]的分析, 该退化成本在短期分析中可以认为是线性模型。本文采用等效功率损耗成本系数描述电池单次充放电折损成本。因此, 多社区整体储能装置的合作运行成本Ccomm计算公式为
| $ C_{\text {comm }}=\sum\limits_{t \in T} c_{\text {ess }}\left(P_{\text {all }}^{t, \text { ch }}+P_{\text {all }}^{t, \text { dis }}\right) $ | (13) |
式中: cess——储能装置的功率损耗成本系数, 取0.011元/kWh;
Pallt, ch、Pallt, dis——t时刻多社区的总充电功率、放电功率。
2.2.2 多社区储能约束条件
将多社区内的所有分布式储能看作一个整体, 应同时满足以下相应的储能运行约束条件:
| $ E_{\text {all }}^t=E_{\text {all }}^{t-1}+\eta_{\text {all }}^{\text {ch }} P_{\text {all }}^{t, \text { ch }} \Delta t-\frac{P_{\text {all }}^{t, \text { als }} \Delta t}{\eta_{\text {all }}^{\text {dis }}} $ | (14) |
| $ E_{\mathrm{all}}^0=E_{\mathrm{all}}^{24} $ | (15) |
| $ 0.1 E_{\text {all }, \max } \leqslant E_{\text {all }}^t \leqslant 0.9 E_{\text {all }, \max } $ | (16) |
| $ 0 \leqslant P_{\mathrm{all}, t}^{\mathrm{ch}} \leqslant \varepsilon_{\mathrm{all}, t}^{\mathrm{ch}} P_{\mathrm{all}, \max } $ | (17) |
| $ 0 \leqslant P_{\mathrm{all}, t}^{\mathrm{dis}} \leqslant \varepsilon_{\mathrm{all}, t}^{\mathrm{dis}} P_{\mathrm{all}, \max } $ | (18) |
| $ \varepsilon_{\mathrm{all}, t}^{\mathrm{ch}}+\boldsymbol{\varepsilon}_{\mathrm{all}, t}^{\mathrm{dis}} \leqslant 1 $ | (19) |
| $ P_{\text {all, } \max }=\mu E_{\text {all, } \max } $ | (20) |
| $ P_{\text {all, max }}=\sum\limits_{j \in N} \sum\limits_{i \in M} P_{j, i, \max } $ | (21) |
式中: Eallt、Eallt-1——t时刻和t-1时刻多社区所有储能装置的总电量;
ηallch、ηalldis——总储能装置的充电效率和放电效率;
Eall0、Eall24——总储能装置的初始电量和终止电量;
Eall, max——总储能装置的最大存储电量;
εall, tch、εall, tdis——布尔型变量, 用以保证储能装置不同时充放电;
Pall, max——多社区的最大充放电功率;
N——社区数量;
M——社区内的用户数量。
容量平衡约束条件为
| $ E_{\mathrm{all}}^0=\sum\limits_{j \in N} \sum\limits_{i \in M} E_{j, i}^0 $ | (22) |
| $ E_{\mathrm{all}}^t=\sum\limits_{j \in N} \sum\limits_{i \in M} E_{j, i}^t $ | (23) |
| $ \sum\limits_{i=1}^M B_{i, t}=\sum\limits_{i=1}^M P_{i, t}^{\mathrm{dis}}+\sum\limits_{i=1}^M P_{i, t}^{\mathrm{ch}} $ | (24) |
| $ B_{i, t} \leqslant E_{j, i, \max } $ | (25) |
式中: Bi, t——t时刻用户i的储能容量变化量。
上述约束条件保证了总储能容量变化量等于储能释放量与储能充电量之和, 也保证了每个用户的容量变化量不超过其最大储能容量。
3 合作模型的求解
3.1 广义纳什议价理论
广义纳什议价理论是一种用于描述多方合作决策的博弈理论。该理论消除了对称公理的限制, 根据参与者的贡献大小来分配议价能力, 然后参与者根据自身的议价能力进行谈判以获取相应的利益。基本模型如下:
| $ \left\{\begin{array}{l} \max \prod\limits_{i \in \Omega}\left(U_i-U_i^0\right)^{\alpha_i} \\ \text { s. t. } U_i \geqslant U_i^0 \end{array}\right. $ | (26) |
式中: Ω——全部参与合作的主体;
Ui——主体参与合作后的效益;
Ui0——主体参与合作前的效益, 称为谈判破裂点;
αi——i用户的议价能力, αi>0。
当各参与者在合作中的贡献度存在差异时, 广义纳什议价模型能够更公平地进行利益分配。这是由引入的正参数αi所实现的。该参数的取值反映了参与者在谈判中的议价能力, 这种能力的差异可以根据个体的贡献度按照一定规则计算得到。因此, 广义纳什议价模型相较于一般纳什议价模型更具有实际意义, 能够更好地应用于真实场景中参与者贡献度不同的情况。
3.2 多社区合作运行模型
本文所提出的多社区各主体合作运行模型如下
| $ \left\{\begin{array}{l} \max \left(C_{\text {comm }}-C_{\text {comm }}^0\right) \prod\limits_{\substack{j \in N \\ i \in M}}\left(C_{j, i, \text { user }}^0-C_{j, i, \text { uesr }}\right) \\ \text { s. t. } C_{\text {comm }} \geqslant C_{\text {comm }}^0 \\ C_{j, i, \text { user }}^0 \geqslant C_{j, i, \text { uesr }} \\ \text { 式(1) 式 }(25) \end{array}\right. $ | (27) |
式中: Ccomm0——多社区储能装置合作前的运行成本;
Cj, i, user0、Cj, i, user——j社区i用户在合作前、后的用能成本。
式(27)的合作运行模型本质上是一个非凸非线性问题, 无法借用商业求解器直接求解, 因此本文将其转换为两个子问题, 即合作联盟成本的最小化与合作联盟的收益分配。
3.3 合作联盟成本的最小化
合作联盟成本的最小化问题可描述为
| $ \left\{\begin{array}{l} \min \left[C_{\text {comm }}+\sum\limits_{j \in N} \sum\limits_{i \in M} C_{j, i, \text { user }}\right] \\ \text { s.t. 式(1) } \sim \text { 式 }(25) \end{array}\right. $ | (28) |
由于交替方向乘子算法具有良好的收敛特性和较强的鲁棒性, 可以在保持隐私的同时进行高效的求解, 因此被广泛应用于解决具有可分离变量的优化问题。为了保护各用户参与谈判时的隐私, 本文采用改进交替方向乘子算法对合作联盟成本最小化问题进行求解。基于式(27)和式(28), 对原有交替方向乘子法进行改进, 将用户层面的储能共享与社区层面的储能共享结合起来, 以便进行循环迭代求解。
对于合作联盟成本最小化问题, 令
| $ E_{j, i}^t=\varphi_{j, i}^t $ | (29) |
| $ E_{\mathrm{all}}^t=\sum\limits_{j \in N} \varphi_j^t $ | (30) |
| $ \varphi_j^t=\sum\limits_{i \in N} \varphi_{j, i}^t $ | (31) |
式中: φj, it——j社区i用户的虚拟储能容量;
φjt——j社区的虚拟储能容量。
φj, it是用于社区用户内部的信息交互, 以确定用户的最终共享储能容量使用计划; φjt是用于社区间的信息交互, 以确定各社区最终的储能容量交互计划。
引入拉格朗日对偶乘子ρj.it和εjt, 引入惩罚因子δj, i和δj, 可得式(28)的增广拉格朗日函数L为
| $ \begin{aligned} L= & C_{\text {comm }}+\sum\limits_{j \in N} \sum\limits_{i \in M} C_{j, i, \text { user }}+ \\ & \frac{\delta_j}{2} \sum\limits_{t \in T}\left(E_{\text {all }}^t-\sum\limits_{j \in N} \varphi_j^t+\frac{\varepsilon_j^t}{\delta_j}\right)^2+ \\ & \frac{\delta_{j, i}}{2} \sum\limits_{j \in N} \sum\limits_{i \in M} \sum\limits_{t \in T}\left(\varphi_{j, i}^t-E_{j, i}^t+\frac{\rho_{j, i}^t}{\delta_{j, i}}\right)^2 \end{aligned} $ | (32) |
根据改进交替方向乘子算法, 对式(32)进行分解, 分别可以得到社区内部、社区之间及社区数据中心的分布式优化模型。
社区内部用户的分布式优化模型为
| $ \left\{\begin{array}{l} \min \left[C_{j, i, \text { user }}+\frac{\delta_{j, i}}{2} \sum\limits_{t \in T}\left(\varphi_{j, i}^t-E_{j, i}^t+\frac{\rho_{j, i}^t}{\delta_{j, i}}\right)^2\right] \\ \text { s.t. 式(1) } \sim \text { 式(12) } \end{array}\right. $ | (33) |
社区之间的分布式优化模型为
| $ \left\{\begin{array}{l} \min \left[C_{\text {comm }}+\frac{\delta_j}{2} \sum\limits_{t \in T}\left(E_{\text {all }}^t-\sum\limits_{j \in N} \varphi_j^t+\frac{\varepsilon_j^t}{\delta_j}\right)^2\right] \\ \text { s. t. 式 }(13) \sim \text { 式 }(25) \end{array}\right. $ | (34) |
社区数据中心的分布式优化模型为
| $ \left\{\begin{array}{l} \min \left[\frac{\delta_{j, i}}{2} \sum\limits_{j \in N} \sum\limits_{t \in T}\left(\varphi_{j, i}^t-E_{j, i}^t+\frac{\rho_{j, i}^t}{\delta_{j, i}}\right)^2+\right. \\ \left.\quad \frac{\delta_j}{2} \sum\limits_{t \in T}\left(E_{\text {all }}^t-\sum\limits_{j \in N} \varphi_j^t+\frac{\varepsilon_j^t}{\delta_j}\right)^2\right] \\ \text { s. t. 式 }(31) \end{array}\right. $ | (35) |
基于上述分析, 建立合作联盟成本最小化问题的分布式算法, 具体步骤如下:
步骤1 初始化δj, i、δj、φj, it、ρj, it, 外部迭代次数K=0;
步骤2 对于社区内部的分布式优化, 根据式(33), 求得第K次迭代过程中t时刻j社区i用户储能装置的存储电量Ej, it, K;
步骤3 更新外部迭代次数K=K+1, 更新拉格朗日对偶乘子为
| $ \rho_{j, i}^{t, K+1}=\rho_{j, i}^t+\delta_{j, i}\left(\varphi_{j, i}^{t, K+1}-e_{j, i}^{t, K+1}\right) \rho_{j, i}^{t, K+1} $ | (36) |
步骤4 初始化φjt、εjt, 内部迭代次数k=0;
步骤5 对于社区之间的分布式优化, 根据式(34), 求得第k次迭代过程中t时刻多社区所有储能装置的存储电量Eallt, k, 对于社区数据中心的分布式优化, 根据式(35), 求得φj, it与φjt;
步骤6 更新内部迭代次数k=k+1, 更新拉格朗日对偶乘子为
| $ \varepsilon_j^{t, k+1}=\varepsilon_j^{t, k}+\delta_j\left(E_{\text {all }}^{t, k+1}-\sum\limits_{j \in N} \varphi_j^{t, k+1}\right) \varepsilon_j^{t, k+1} $ | (37) |
步骤7 判断内部循环迭代情况, 若满足以下条件:
| $ \left\|\varepsilon_{k+1}-\varepsilon_k\right\| \leqslant \xi_1 $ | (38) |
则继续进行, 否则返回步骤5继续重复计算, 其中ξ1为内循环收敛判定系数;
步骤8 令φK=φk, 判断外部循环迭代情况, 若满足条件:
| $ \left\|\rho_{K+1}-\rho_K\right\| \leqslant \xi_2 $ | (39) |
则终止迭代并输出结果, 否则返回步骤2继续重复计算, 其中ξ2为外循环收敛判定系数。
3.4 合作联盟的收益分配
合作联盟的收益即为合作前的成本与合作后的最小成本之差。合作联盟的整体收益Rall的计算公式为
| $ R_{\mathrm{all}}=C_{\mathrm{comm}}^0-C_{\mathrm{comm}}+\sum\limits_{j=1}^N \sum\limits_{i=1}^M\left(C_{j, i, \text { uesr }}^0-C_{j, i, \text { user }}\right) $ | (40) |
结合分布式储能容量的交互情况, 本文采用一种非线性映射方法计算各用户在合作中的贡献度, 即议价能力αi。
合作联盟内各用户提供的共享储能容量Dish与使用的共享储能容量Diuse分别为
| $ D_i^{\mathrm{sh}}=\sum\limits_{t \in T} D_{i, t}^{\mathrm{sh}} \Delta t $ | (41) |
| $ D_i^{\mathrm{use}}=\sum\limits_{t \in T} D_{i, t}^{\mathrm{use}} \Delta t $ | (42) |
式中: Di, tsh——t时刻i用户计划提供的储能容量;
Di, tues——t时刻i用户计划使用的储能容量。
定义Dmaxsh=max{Dish, i∈M}, d1=Dish/Dmaxsh, Dmaxues=max{Diues, i∈M}, d2=Diuse/Dmaxuse, 则i用户的议价能力为
| $ \alpha_i=\mathrm{e}^{d_1}-\mathrm{e}^{-d_2} $ | (43) |
式(43)是非线性能量映射函数, 且αi为正参数。这说明在合作过程中, 每个提供储能容量与使用储能容量的用户都做出了积极的贡献, 并且提供储能容量的用户比使用储能容量的用户贡献度更大。
基于上述分析, 构建并求解基于广义纳什议价理论的合作联盟收益分配模型为
| $ \left\{\begin{array}{l} \max \prod\limits_{\substack{j \in N \\ i \in M}}\left(U_{j, i}-U_{j, i}^0\right) \alpha_i \\ \text { s.t. } U_{j, i} \geqslant U_{j, i}^0 \end{array}\right. $ | (44) |
此时, 合作联盟整体收益Rall、合作运行成本Ccomm与各用户议价能力αi已知, 式(44)可转化为
| $ \left\{\begin{array}{l} \max \sum\limits_{j \in N} \sum\limits_{i \in M} \alpha_i \ln \left(U_{j, i}-U_{j, i}^0\right) \\ \text { s.t. } U_{j, i} \geqslant U_{j, i}^0 \end{array}\right. $ | (45) |
4 算例分析
4.1 仿真环境设置
本文通过在某多社区微网中进行仿真分析来验证分布式储能双层共享模式及利益分配策略的有效性。多社区微网拓扑图如图 2所示。该微网由3个社区组成, 每个社区均包含12个用户。其中, A社区的用户全部配备了光伏发电和储能装置, B社区的用户全部配备了风力发电和储能装置, C社区的用户则没有配备发电设备和储能装置。
假设A社区与B社区所有用户的储能容量均为500 kWh, 充放电功率限额均为100 kW, 且充放电效率均为0.92。在模拟实验中, 设定上网电价为零, 即电网不收购用户多余的电能。假设相邻社区之间存在使其相互连接的基础设施, 可实现不同社区之间的储能共享。
4.2 储能共享策略分析
本文设置如下3个场景: 场景1, 用户之间不进行储能共享, 自储自用; 场景2, 仅社区内部用户之间进行储能共享, 社区之间不进行储能共享; 场景3, 本文提出的分布式储能双层共享策略。以上3种场景的仿真参数与环境设置均保持一致。3种场景下的仿真结果如表 1所示。
表 1
各场景下的仿真结果
| 场景 | 用电成本 | 运行成本 | 储能损耗成本 | 总成本 | |||||
| A社区 | B社区 | C社区 | A社区 | B社区 | C社区 | ||||
| 1 | 26 208.68 | 26 375.70 | 31 805.65 | 154.42 | 142.06 | 0 | 296.48 | 84 686.51 | |
| 2 | 25 412.25 | 24 920.46 | 31 805.65 | 165.76 | 184.28 | 0 | 350.04 | 82 488.40 | |
| 3 | 26 574.16 | 25 409.28 | 27 260.45 | 176.01 | 192.64 | 0 | 368.65 | 79 612.57 | |
由表 1可以看出, 与场景1和场景2相比, 采用分布式储能双层共享策略的场景3的总成本得到了一定比例的降低, 经济性得到了一定程度的提升。从场景1到场景3, 储能损耗成本逐步增加。这说明多社区分布式储策略会增加储能装置的动作频率, 进而增加储能的运行维护成本, 但通过更高效的能量管理和资源调度, 可以有效整合和合理共享储能资源, 促进分布式可再生能源的消纳, 使得共享储能系统的的整体效益得到提升。
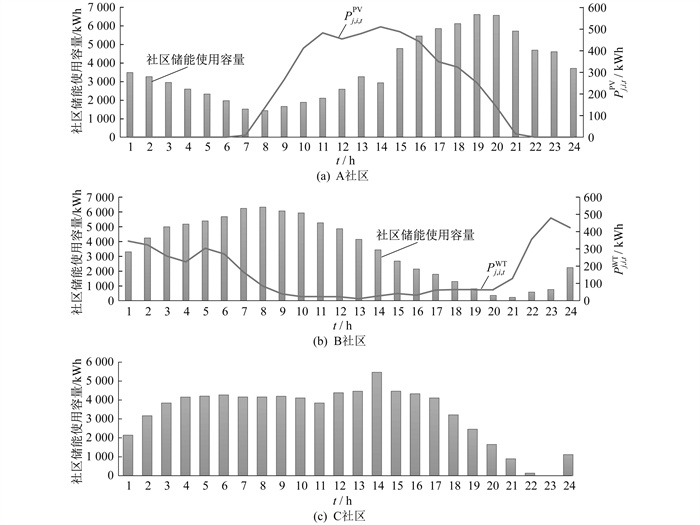
本文以夏季某一典型日为例进行仿真分析, 得到各社区分布式储能共享情况如图 3所示。
由图 3可以看出, A社区的主要充电时段为7:00—19:00, 其他时段则以放电为主, 与光伏发电装置的出力时段较为一致; A社区在12:00调用的共享储能容量的峰值已超过A社区的整体储能容量6 000 kWh; 配备有风力发电装置的B社区的储能容量使用情况与A社区类似; 没有配备分布式发电装置和储能装置的C社区, 也可以参与储能共享进行削峰填谷, 改善自身负荷曲线。从整体上看, 社区合作联盟的整体储能主要放电时段为9:00—12:00和16:00—22:00, 与用户的用电负荷高峰期相重合。通过多社区的分布式储能共享, 可以根据不同社区的用能特点和发电特点, 实现储能容量的最优分配和储能的规模效应。
4.3 利益分配合理性分析
根据表 1数据计算可知, 合作联盟的整体收益为5 703.94元。基于广义纳什议价理论, 根据各用户在储能共享过程中的贡献度进行非对称的利益分配。两种议价理论下社区间收益分配和C社区各用户收益分配分别如表 2和表 3所示。
表 2
社区间收益分配
| 社区 | 标准纳什议价理论 | 广义纳什议价理论 |
| A | 1 901.31 | 3 593.48 |
| B | 1 901.31 | 1 540.06 |
| C | 1 901.31 | 570.39 |
表 3
C社区各用户收益分配
| 用户 | 标准纳什议价理论 | 广义纳什议价理论 | 用户 | 标准纳什议价理论 | 广义纳什议价理论 | |
| 用户25 | 158.44 | 36.82 | 用户31 | 158.44 | 44.57 | |
| 用户26 | 158.44 | 39.75 | 用户32 | 158.44 | 41.92 | |
| 用户27 | 158.44 | 46.24 | 用户33 | 158.44 | 58.73 | |
| 用户28 | 158.44 | 42.73 | 用户34 | 158.44 | 57.76 | |
| 用户29 | 158.44 | 47.62 | 用户35 | 158.44 | 62.27 | |
| 用户30 | 158.44 | 49.28 | 用户36 | 158.44 | 42.70 |
由表 2和表 3可以看出, C社区收益最少, 且各用户收益分配差别较小。这是由于在合作过程中, C社区各用户无法直接提供储能或发电方面的贡献, 故该社区内各用户应被赋予最小的收益份额。
在标准纳什议价理论下, 每个社区整体的收益几乎相等, 为1 901.31元, 其中C社区每个用户的收益也相等, 为158.44元。然而, 当各社区与用户在合作中的能量贡献大小存在差异时, 这种分配方式显然不公平。相比之下, 本文所提出的基于广义纳什议价理论的收益分配方法, 可以根据各参与主体的贡献度进行收益分配, 确保了更加公正的分配结果。
5 结语
本文提出了一种多社区分布式储能共享运行策略。通过理论验证与仿真分析发现: 该策略可以有效整合储能资源的规模效应, 从而提高经济效益; 基于广义纳什议价理论的收益分配策略能够对合作后的收益进行公平合理的分配, 有利于激发合作参与者的积极性, 推进合作的良性运行。本文研究的日运行优化策略中暂未考虑不确定性的影响, 如可再生能源出力与用户负荷的不确定性, 因此将不确定性纳入运行决策是下一步工作的重点内容。
参考文献
-
[1]康重庆, 刘静琨, 张宁. 未来电力系统储能的新形态: 云储能[J]. 电力系统自动化, 2017, 41(21): 2-8. DOI:10.7500/AEPS20170601011
-
[2]刘静琨, 张宁, 康重庆. 电力系统云储能研究框架与基础模型[J]. 中国电机工程学报, 2017, 37(12): 3361-3371.
-
[3]刘娟, 邹丹平, 陈毓春, 等. "互联网+"的客户侧分布式储能P2P共享模式运营机制及效益探讨[J]. 电网与清洁能源, 2020, 36(4): 97-105.
-
[4]夏元兴, 徐青山, 黄煜, 等. 端对端交易场景下配电网分布式储能的优化配置[J]. 电力系统自动化, 2021, 45(14): 82-89.
-
[5]李轩, 李华强, 李旭翔. 基于区块链的分布式储能端对端交易控制方法[J]. 电网技术, 2021, 45(9): 3424-3431.
-
[6]李山山, 李华强, 金智博, 等. 基于共享经济理念的园区分布式能源共享服务机制[J]. 中国电机工程学报, 2022, 42(1): 56-70.
-
[7]穆程刚, 丁涛, 曲明, 等. 基于区块链的表后微网系统及其点对点能量块交易模型设计[J]. 中国电机工程学报, 2021, 41(20): 6927-6940.
-
[8]马腾飞, 裴玮, 肖浩, 等. 基于纳什谈判理论的风-光-氢多主体能源系统合作运行方法[J]. 中国电机工程学报, 2021, 41(1): 25-39.
-
[9]刘轶涵, 徐青山, 杨永标, 等. 计及配电网潮流约束下基于广义纳什议价理论的工业用户共享储能配置[J]. 电网技术, 2023, 47(2): 571-583.
-
[10]王帅, 帅轩越, 王智冬, 等. 基于纳什议价方法的虚拟电厂分布式多运营主体电能交易机制[J]. 电力建设, 2022, 43(3): 141-148.
-
[11]马云聪, 武传涛, 林湘宁, 等. 一种基于半分布式结构化拓扑的云储能点对点交易策略研究[J]. 中国电机工程学报, 2022, 42(21): 7731-7745.
-
[12]顾欣, 王琦, 胡云龙, 等. 基于纳什议价的多微网综合能源系统分布式低碳优化运行策略[J]. 电网技术, 2022, 46(4): 1464-1475.
-
[13]CUI S, WANG Y W, SHI Y, et al. An efficient Peer-to-Peer energy sharing framework for numerous community prosumers[J]. IEEE Transactions on Industrial Informatics, 2019, 16(12): 7402-7412.
-
[14]吴锦领, 楼平, 管敏渊, 等. 基于非对称纳什谈判的多微网电能共享运行优化策略[J]. 电网技术, 2022, 46(7): 2711-2721.
-
[15]刘可真, 董敏, 杨春昊, 等. 基于纳什谈判的智能园区P2P电能交易优化运行[J]. 电力自动化设备, 2023, 43(5): 45-53.
-
[16]陈岑, 武传涛, 康慨, 等. 基于改进Owen值法的分布式储能双层合作博弈优化策略[J]. 中国电机工程学报, 2022, 42(11): 3924-3935.