|
|
|
发布时间: 2023-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-07-14
基金项目: 国家自然科学基金(51977128)
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2023)06-0543-06
|
摘要
由于配电网缺少高效的面向分布式有功潮流最优化问题的集群划分方法,因此优化和改进了基于遗传算法的配电网集群划分策略。首先,考虑到配电网台区终端计算能力有限,以及各集群强度须达标的条件,定义集群划分的节点限制指标,使集群划分结果更加合理。然后,对遗传算法进行改进,提高了遗传算法在解决集群划分问题时的收敛速度,增强了全局寻优能力。最后,在MATLAB仿真平台上对IEEE-33节点系统进行实验,验证了所提出指标的合理性以及改进算法的有效性。
关键词
分布式电源; 配电网; 集群划分; 遗传算法
Abstract
Due to the situation that the distribution network lacks efficient cluster division strategy for the optimization of distributed active power flow, this paper optimizes and improves the distribution network cluster division strategy based on genetic algorithm.First of all, considering the limited computing capacity of the terminal in the distribution network area and the condition that the strength of each cluster must meet the standard, the node limit index of cluster division is defined to make the result of cluster division more reasonable.Then, the mechanism of genetic algorithm is improved, the convergence speed of genetic algorithm is improved, and the global optimization ability is enhanced.Finally, simulations are carried out on IEEE-33 nodes system on MATLAB simulation platform to verify the rationality of the proposed index and the effectiveness of the improved algorithm.
Key words
distributed power generation; distribution network; cluster division; genetic algorithm
自国家提出“双碳”目标, 鼓励大力发展新型电力系统以来, 智能电网、新能源消纳并网、系统灵活性、可靠性提升等课题逐渐成为电力网络领域的研究重点[1]。新能源并入电网的容量逐渐扩大, 接入方式也由主网大容量集中接入转变为在配电网以小容量的分布式电源零散馈入, 同时产生了潮流倒送、电压越限等威胁到配电网电压质量和系统稳定性的风险因素[2]。另外, 大量分布式电源(Distributed Generator, DG)、储能(Energy Storage, ES)、柔性负荷等可控资源加入主动配电网(Active Distribution Network, ADN), 使得配电网需要监测和调控的电力电子设备数量激增, 面临数据海和维数灾的问题。然而, 配电网的智能化水平相对主网较为落后, 且点多面广、升级成本巨大[3]。
DG接入量较少时不成片区化, 对ADN影响较小, 管理相对松散。随着新能源渗透率的提高, DG的接入数量增多, 容量增大, 逐渐呈现出片区化、集群化的趋势, 对ADN的影响也逐渐增大, 必须进行合理规划。结合ADN数据量庞大的特点, 可采用集群化管理方式, 实现DG的有序运行, 并参与电网调度[4]。
文献[5]通过集群划分的方式优化无功功率, 达到调节系统电压的目的。文献[6]借助二阶锥规划对具有高度非线性的目标函数和约束条件进行处理, 将构造的优化问题转换为线性度更好的二阶锥规划模型, 并应用于面向分布式电源大规模接入的配电系统无功优化。文献[7]应用Bender’s分解法和电网分区解决无功规划优化问题。但文献[5-7]均专注于无功调压领域, 并未关注到配电网的有功资源调度, 因此使用的指标沿用了无功优化问题的假设条件, 偏离了有功优化问题的物理情景, 准确度较低。文献[8]使用综合指标及遗传算法对ADN进行分区, 并采用同步交替方向乘子法对分区后的ADN进行有功-无功协同优化, 但并未对集群划分的理论和算法进行深入探究, 而是在出现不合理分区时, 手动剔除不合理的分区方案。
当前遗传算法的运用已经较为成熟, 常用的改进措施有自适应交叉变异率和精英保留策略[9-10]。其中, 自适应交叉变异率考虑到后期遗传算法中个体趋同的问题, 减小交叉率, 增加变异率, 具有增加局部寻优能力的作用。精英保留策略通过保护性能最优个体, 提高了遗传过程的容错性。经过多次仿真实验发现, 以上改进虽然能在一定程度上提高遗传算法的收敛速度, 但对遗传算法的全局寻优能力没有提升, 当遗传算法陷入早熟时, 以上策略极难跳出局部最优解。
本文所提出的电气距离指标, 使用全新的假设代替无功优化问题中使用的假设, 更加符合有功潮流优化问题的物理场景; 定义了新的节点限制指标, 能够有效规避规模不合理的分区结果, 有助于准确寻得最优解; 对遗传算法的机制进行改进, 使得算法在具有足够多的迭代次数时总能寻到最优解, 大大提升了遗传算法的寻优速度和全局寻优能力。
1 集群划分理论
1.1 模块度函数
模块度函数可用于衡量集群内部各个节点的关联程度[11-12]。其公式为
| $\rho=\frac{1}{2 m} \sum\limits_i \sum\limits_j\left(e_{i j}-\frac{k_i k_j}{2 m}\right) \delta(i, j)$ | (1) |
| $m=\frac{1}{2} \sum\limits_i \sum\limits_j e_{i j}$ | (2) |
| $k_i=\sum\limits_j e_{i j}$ | (3) |
式中: ρ——模块度;
m——所有边权之和;
eij——节点i与节点j之间的边权;
ki、kj——所有与节点i、节点j直接相连的边权和;
δ(i, j)——0-1变量, 节点i与节点j处于同一集群时取1, 否则取0。
1.2 潮流方程和分块雅可比矩阵
在电力系统潮流变化的过程中, 存在以下关系:
| $\left[\begin{array}{c}\Delta \boldsymbol{P} \\ \Delta \boldsymbol{Q}\end{array}\right]=\left[\begin{array}{ll}\boldsymbol{J}_{\mathrm{P} \mathtt{θ}} & \boldsymbol{J}_{\mathrm{PV}} \\ \boldsymbol{J}_{\mathrm{Q} \mathtt{θ}} & \boldsymbol{J}_{\mathrm{QV}}\end{array}\right]\left[\begin{array}{c}\Delta \boldsymbol{\theta} \\ \Delta \boldsymbol{U}\end{array}\right]$ | (4) |
式中: ΔP——节点注入功率的有功功率增量;
ΔQ——节点注入功率的无功功率增量;
JPB、JPV、JQB、JQV——潮流修正方程系数矩阵中的方块;
Δθ——节点电压的相角增量;
ΔU——节点电压的幅值增量。
潮流修正方程系数矩阵为雅可比矩阵, 可在牛顿-拉夫逊法求解潮流数据收敛前的最后一次变量更新过程中求得。
1.3 电气距离
现有研究中, 通常先求得无功电压灵敏度矩阵, 再构造电气距离[13]。
将式(4)重写为
| $\left\{\begin{array}{l}\Delta \boldsymbol{P}=\boldsymbol{J}_{\mathrm{P} \mathtt{θ}} \Delta \boldsymbol{\theta}+\boldsymbol{J}_{\mathrm{PV}} \Delta \boldsymbol{U} \\ \Delta \boldsymbol{Q}=\boldsymbol{J}_{\mathrm{Q} \mathtt{θ}} \Delta \boldsymbol{\theta}+\boldsymbol{J}_{\mathrm{QV}} \Delta \boldsymbol{U}\end{array}\right.$ | (5) |
无功-电压灵敏度方程的推导是以固定的有功潮流为基础, 因此假设有功功率增量为零, 将ΔP=0代入式(5)并进行变形整理得到:
| $\Delta \boldsymbol{U}=\left(\boldsymbol{J}_{\mathrm{QV}}-\boldsymbol{J}_{\mathrm{Q} \mathtt{θ}} \boldsymbol{J}_{\mathrm{P} \mathtt{θ}}^{-1} \boldsymbol{J}_{\mathrm{PV}}\right)^{-1} \Delta \boldsymbol{Q}$ | (6) |
定义无功电压灵敏度矩阵SVQ为
| $\boldsymbol{S}_{\mathrm{VQ}}=\left(\boldsymbol{J}_{\mathrm{QV}}-\boldsymbol{J}_{\mathrm{Q} \mathtt{θ}} \boldsymbol{J}_{\mathrm{P} \mathtt{θ}}^{-1} \boldsymbol{J}_{\mathrm{PV}}\right)^{-1}$ | (7) |
令:
| $d_{i j}=\lg \left[\frac{S_{\mathrm{VQ}}(j, j)}{S_{\mathrm{VQ}}(i, j)}\right]$ | (8) |
式中: SVQ(i, j)——SVQ中第i行第j列的元素。
dij的取值范围为(0, ∞), 反映了节点j电压变化量对节点i电压变化量的贡献程度, 两节点的电压关联越紧密其值越小。该变化趋势与距离的概念相符, 但是节点间的影响不仅与自身有关, 还与系统中其他节点有关, 因此将两节点间电气距离定义为这两节点与系统中所有其他节点的距离的方差。
定义电气距离Lij为
| $L_{i j}=\sqrt{\left(d_{i 1}-d_{j 1}\right)^2+\left(d_{i 2}-d_{j 2}\right)^2+\cdots+\left(d_{i n}-d_{j n}\right)^2}$ | (9) |
2 考虑节点限制的ADN集群划分策略
2.1 集群划分评价指标
集群划分的考量因素主要包括: 集群内部的有功电源出力和有功负荷大致平衡, 降低集群间的功率互济强度, 使各个集群自我调节互不干扰[6]; 集群内部节点联系紧密, 具有较高的电压相关性, 有利于集群电压质量调节的相互独立; 集群的节点数量应维持在合理区间, 避免过大集群和孤立节点。综上, 本文所采用的集群划分综合评价指标F为
| $\max F=\lambda_1 f_1+\lambda_2 f_2+\lambda_3 f_3$ | (10) |
式中: λ1、λ2、λ3——有功平衡度指标、电气距离指标、节点限制指标的权重;
f1、f2、f3——有功平衡度指标、电气距离指标、节点限制指标。
2.2 有功平衡度指标
有功平衡度指标又称为功率特性指标, 属于功能性指标, 反映了集群内的节点净功率互补程度。该指标数值越高, 代表新能源消纳水平越高。为便于后续的指标计算, 本文采用以相邻节点互补程度为边权的模块度函数形式[6]。
表征节点互补程度的边权公式为
| $e_{i j}=1-\frac{\left|\sum\limits_t P_i(t)+\sum\limits_t P_j(t)\right|}{\max\limits_{i, j}\left|\sum\limits_t P_i(t)+\sum\limits_t P_j(t)\right|}$ | (11) |
式中: Pi(t)、Pj(t)——节点i和节点j的净功率特性, 取注入节点方向为正。
将式(11)代入式(1)~式(3)即可得到有功平衡度指标f1。
2.3 节点限制指标
以有功平衡度为功能性指标, 电气距离指标为结构性指标, 两者相结合在一定程度上能够使集群划分的结果相对更加合理。但经过仿真实验发现, 仅考虑结构性和功能性两个指标所得出的分区结果, 会出现集群过大和过小两种极端情况。过大的分区在边缘计算中会导致维数灾问题, 使分区和分布式算法失去作用。过小的分区不具备足够的自我调节能力, 无法做到相对独立。
为了避免极端分区的出现, 定义节点限制指标为
| $f_3=\prod\limits_{i=1}^N f_{\mathrm{cl}} f_{\mathrm{ch}}$ | (12) |
| $f_{\mathrm{cl}}=\left\{\begin{array}{l}\mathrm{e}^{-\frac{\left(c-c_l\right)^2}{\sigma_1}}, \quad 0 \leqslant c \leqslant c_1 \\ 1, \quad c>c_1\end{array}\right.$ | (13) |
| $f_{\mathrm{ch}}=\left\{\begin{array}{l}1, \quad 0 \leqslant c \leqslant c_{\mathrm{h}} \\ \mathrm{e}^{-\frac{\left(c-c_{\mathrm{h}}\right)^2}{\sigma_2}}, \quad c>c_{\mathrm{h}}\end{array}\right.$ | (14) |
式中: N——划分方案中的集群数量;
fcl、fch——节点数量下限和上限评分;
c——第i个集群中的节点数量;
cl、ch——可接受的节点数量下限和上限;
σ1、σ2——针对节点下限和上限的可调节参数。
σ1和σ2越大代表对于单集群节点数量超出限制的容忍度越高, σ1和σ2均取正值。
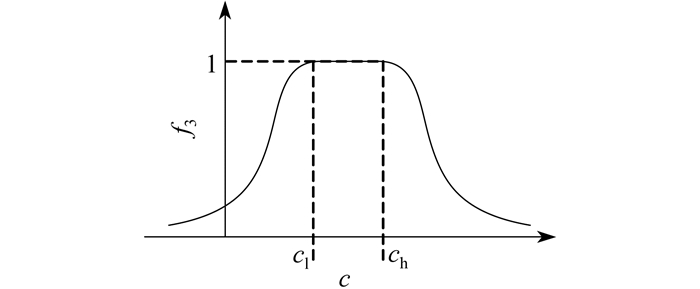
节点限制指标的示意图如图 1所示。
由图 1可以看出: f3在集群节点数量较为合理时, 其值保持为1;当划分方案出现过大集群或孤立节点时, 指标数值将会急剧下降, 作为对不合理集群的惩罚。这一惩罚程度可由σ1和σ2进行调节。
2.4 改进遗传算法
由于遗传算法的遗传个体保存形式为0-1代码, 与代表网络拓扑的无权邻接矩阵具有良好的适配性, 同时遗传代码被赋予了直接的拓扑意义, 可以通过对遗传代码的元素控制来间接影响分区取向, 因此本文选用遗传算法求解集群划分问题。
通过大量的遗传算法实验观察发现, 遗传过程中种群会在初期呈现寻优状态。在迭代一定次数后, 寻得了相对更优个体的种群会不可避免地进入繁殖趋同时期。优势个体通常会在7~8代后数量扩张至整个种群, 进而使遗传算法陷入早熟。其全局寻优能力主要依靠变异率。但是, 为了保持遗传能够顺利进行, 通常将变异率设置得很低, 以至于很难通过变异寻得全局最优解。
为解决遗传算法的早熟问题, 本文通过对遗传过程中的种群进行数量控制来遏制遗传的个体同一化趋势, 并提高遗传算法的全局寻优能力。
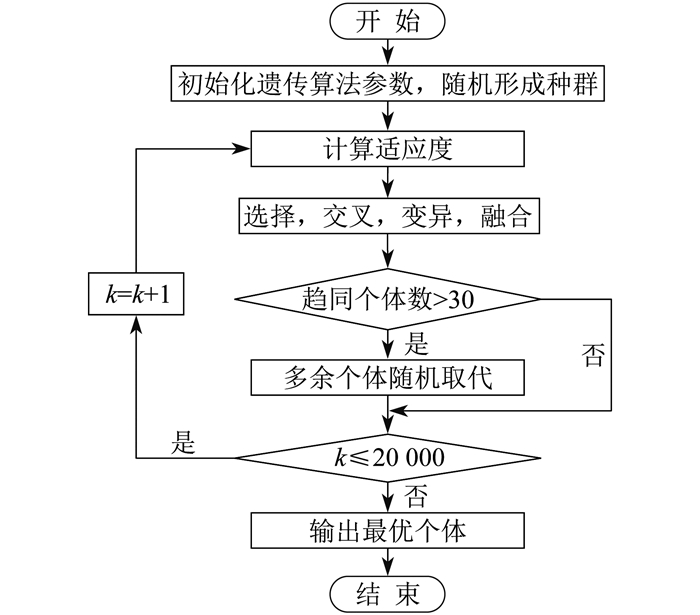
改进遗传算法的逻辑结构如图 2所示。其中, k为迭代次数。
图 2中的选择和交叉部分导致遗传个体出现了同一化趋势。在产生具有优势的个体后, 轮盘赌选法和交叉互换的过程将会产生封闭趋势, 使优势个体数量迅速增加。与此同时, 种群数量却恒定不变, 进而使优势个体数量膨胀至种群容量。本文在次迭代交叉互换后的时间点插入数量检测机制, 令任何个体的数量不能超过总体数量的一定比例, 超出部分替换为全局的随机新个体。在使用上述改进后, 个体同一化的趋势被强制地限制了, 但趋同仍旧发生, 具体体现为每一次迭代的同一化个体数量检测仍会超出限制。个体同一化的趋势是伴随遗传特性一起出现的, 是遗传算法无法避免的趋势, 因此每次迭代都会引入一定数量的全局随机个体, 于是趋同性被转化为全局寻优能力。
3 算例分析
3.1 仿真模型介绍
3.2 节点限制指标验证及集群划分结果
本文在优化实例中将各指标的参数设置如下: λ1=0.4;λ2=0.6;λ3=0.5;ch=12;cl=4;σ1=4;σ2=1;cosφ=0.8;k=0.75。使用上述参数但未加入节点限制指标, 即评价指标为maxF=λ1f1+λ2f2时, 集群划分结果如图 3所示。
图 3中, 虚线代表划分出的集群, 有5个集群负荷容量过小; 节点23和节点24因为设置了大型工业负荷, 形成了较大的功率缺额, 在有功平衡度指标的作用下, 抢占了干线上的多个具有功率盈余的DG节点, 最终形成了包含17个节点的巨型集群。
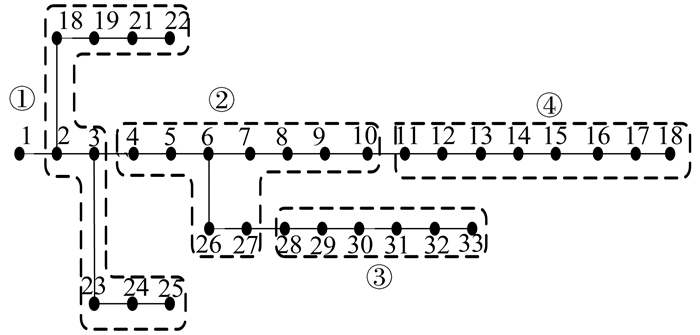
在使用节点限制指标后, 集群划分评价指标为式(10), 划分结果如图 4所示。图 4中, 共有4个集群, 2个9节点集群, 1个8节点集群和1个6节点集群。
表 2
集群划分后各集群的参数
| 集群编号 | 节点数目 | 负荷容量/kVA | 有功净负荷/kW |
| 1 | 9 | 1 565.41 | 280 |
| 2 | 9 | 975.09 | -170 |
| 3 | 6 | 894.43 | 50 |
| 4 | 8 | 547.95 | -45 |
由表 2可以看出, 各集群规模符合指标限制, 集群2、集群3、集群4的有功净负荷相较集群负荷总容量不超过20%。集群1包含大型工业负荷, 有功净负荷较大, 但其靠近ADN首端, 电压稳定性较好, 调节能力较强。该集群划分方案能够较好地完成前文所述目标。
3.3 遗传算法性能对比
本文的遗传算法参数设计如下: 初始种群规模为200;个体长度为32;迭代次数为20 000次; 杂交率为0.3;选择率为0.5;变异率为0.000 1~0.000 5, 随迭代次数线性增长。
为了衡量改进遗传算法的性能, 采集遗传算法迭代过程中个体进化时的迭代次数。大部分实验样本能在万次级别以下的迭代中经由4~8次进化后达到收敛。由于全局迭代次数过多, 进化过程图像不直观, 且前几次进化过程统计意义不大, 因此本文仅统计每个样本的最后一次进化, 即最优个体出现时的迭代次数, 用以衡量算法的收敛速度。
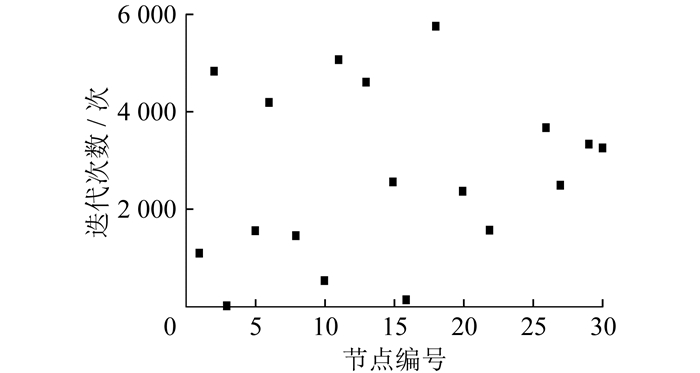
在相同参数下, 对两种遗传算法各采集40次迭代样本。传统遗传算法的18次最优个体出现时的迭代次数如图 5所示。另外, 有7次最优个体出现时的迭代次数超过6 000 (其中有3次超过10 000), 未在图中展示; 还有15次未能收敛至最优结果。最终计算收敛率为62.5%, 平均收敛迭代次数为5 374.6。
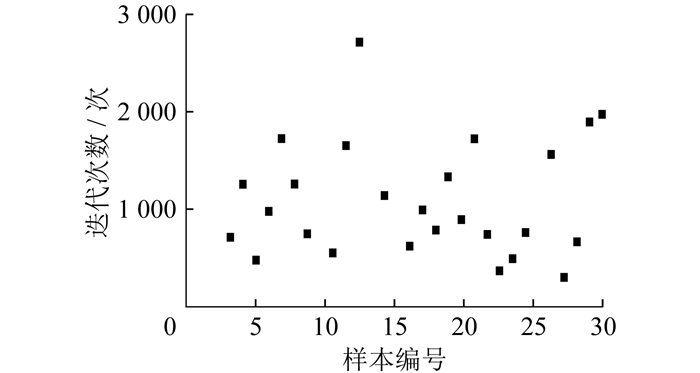
改进遗传算法的26次最优个体出现时的迭代次数如图 6所示。
对于改进遗传算法, 大部分样本都能在3 000次迭代以内收敛至最优结果, 有6次最优结果出现时的迭代次数超过3 000(其中有2次超过10 000);还有8次迭代没有收敛至最优。最终计算收敛率为80%, 相比传统遗传算法提高了28%, 平均收敛迭代次数为3 709.9, 相比传统遗传算法降低了31.0%。
由于改进遗传算法使每次迭代的流程更加复杂, 因此单次迭代耗时更长。传统遗传算法每10 000次迭代耗时1 068.6 s, 而改进遗传算法每10 000次迭代耗时1 327.7 s, 增加了24.25%。但由于算法优化使得收敛所需的迭代次数大大减少, 因此收敛用时仍减少了14.27%。
以上数据说明改进遗传算法相比传统遗传算法性能有大幅提升, 证明了策略的有效性。
4 结语
ADN中接入多种类的中小规模分布式电源, 以及大面积接入可调度的柔性负荷, 是今后相关研究的重要内容。本文基于上述场景, 提出了使集群均匀化、合理化的规模控制指标, 并改进遗传算法的运行逻辑, 提高了遗传算法的收敛速度和寻优能力。最后在MATLAB仿真平台上验证了指标的合理性和算法的有效性。
参考文献
-
[1]马钊, 梁永亮, 尚宇炜, 等. CIGRE SC6 2020专题报道暨主动配电系统发展动向与展望[J]. 电网技术, 2021, 45(4): 1471-1479.
-
[2]刘洪, 徐正阳, 葛少云, 等. 考虑储能调节的主动配电网有功—无功协调运行与电压控制[J]. 电力系统自动化, 2019, 43(11): 51-58.
-
[3]王鹏, 林佳颖, 宁昕, 等. 配电网全景信息感知架构设计[J]. 高电压技术, 2021, 47(7): 2293-2300.
-
[4]肖传亮. 基于集群划分的主动配电网电压控制与优化调度[D]. 合肥: 合肥工业大学, 2020.
-
[5]林少华, 吴杰康, 莫超, 等. 基于二阶锥规划的含分布式电源配电网动态无功分区与优化方法[J]. 电网技术, 2018, 42(1): 238-246.
-
[6]胡迪. 含分布式可再生能源集群的配电系统规划研究[D]. 合肥: 合肥工业大学, 2020.
-
[7]李晓华, 杨尔滨, 杨欢红. 基于电网分区和遗传算法的配电网无功规划优化[J]. 上海电力学院学报, 2009, 25(3): 225-228.
-
[8]赵晶晶, 朱炯达, 刘帅, 等. 基于集群划分的配电网多时间尺度分布式有功-无功协同优化方法[J/OL]. 电测与仪表, 2022: 1-10[2023-02-13]. http//kns. cnki. net/kcins/detail/23.1202. TH. 20220610.1827.008. html.
-
[9]刘健, 李京航, 柏小丽. 基于精英保留策略遗传算法的配电网无功优化[J]. 电气技术, 2015(4): 35-38.
-
[10]孙明华, 崔海涛, 温卫东. 基于精英保留遗传算法的连续结构多约束拓扑优化[J]. 航空动力学报, 2006(4): 732-737.
-
[11]魏震波, 关翔友, 刘梁豪. 电网社区结构发现方法及其应用综述[J]. 电网技术, 2020, 44(7): 2600-2609.
-
[12]丁明, 方慧, 毕锐, 等. 基于集群划分的配电网分布式光伏与储能选址定容规划[J]. 中国电机工程学报, 2019, 39(8): 2187-2201.
-
[13]丁明, 刘先放, 毕锐, 等. 采用综合性能指标的高渗透率分布式电源集群划分方法[J]. 电力系统自动化, 2018, 42(15): 47-52.