|
|
|
发布时间: 2024-02-28 |
特约专栏:风电运行与控制技术 |
|
|
|
收稿日期: 2023-05-30
基金项目: 国网科技项目(4000-201999350A-0-0-00)
中图法分类号: TM732
文献标识码: A
文章编号: 2096-8299(2024)01-0002-08
|
摘要
近年来, 次/超同步振荡(S/SSO)问题严重影响了电力系统的安全运行。在建立了直驱风电机组与直驱风电场等值阻抗模型的基础上, 推导出直驱风电场发生场-网振荡的必要条件, 并通过分析机组出力变化对系统导纳模型的影响, 提出了一种基于功率调整的振荡事故后振荡恢复策略。通过MATLAB/Simulink仿真, 验证了所提策略能在保持直驱风电场出力水平的基础上消除振荡。
关键词
直驱风电场; 次/超同步振荡; 频率耦合; 阻抗模型; 振荡后抑制
Abstract
In recent years, the sub/sup-synchronous oscillation (S/SSO) problem has seriously affected the safe operation of power system. This paper establishes the impedance model of wind farm based on the actual collecting network structure, considering the different unit operating conditions, and obtains the difference analysis of the contributing factors of different wind turbines to the actual oscillation of the grid-connected system. Through the analysis of the impact of the change of the actual wind farm wind turbine operating state on the system admittance model, a power adjustment-based oscillation elimination strategy after the oscillation accident is proposed. The proposed oscillation recovery strategy can eliminate oscillations while maintaining the output level of the direct drive wind farm is validated in the simulation of MATLAB/Simulink.
Key words
PMSG wind farm; sub/sup-synchronous oscillation; frequency couplings; impedance models; oscillation elimination
随着风电技术的发展与风电机组单机容量的提升, 采用永磁同步发电机(Permanent Magnetic Synchronous Generator, PMSG)的直驱风电机组在风电领域获得了广泛的应用。PMSG在并网系统中含有大量的电力电子设备, 使得并网系统存在多时间尺度的复杂动态特性。其中, 直驱风电场与电网交互作用引起的次/超同步振荡(Sub/Sup-Synchronous Oscillation, S/SSO)问题对电力系统稳定运行造成了严重的影响[1]。
目前, 国内外学者针对PMSG并网系统的S/SSO稳定性进行了多方面的研究。文献[2-3]基于特征值分析法, 针对单机无穷大系统, 分析了锁相环控制参数、电流内环控制参数及电网强度对系统振荡模态的影响, 表明控制参数不当是诱发直驱风电场发生S/SSO的主导因素。由于特征值分析方法在针对具备多台风电机组的并网系统时存在“维数灾”问题[4], 所以目前的主流分析方法为阻抗分析法。根据线性化过程中选取坐标系的区别, 阻抗分析法分为dq轴阻抗[5]、序阻抗[6]和极坐标阻抗[7]。文献[8]提出了并网逆变器由于dq轴控制的不对称性而导致系统存在的频率耦合现象。文献[9-12]采用阻抗分析法, 通过频域灵敏度分析, 发现并网逆变器电流内环、电压外环、锁相环控制增益变化对系统振荡模态的影响。文献[13]通过考虑变压器及汇集线路阻抗, 建立了计及频率耦合的多逆变器并网系统模型。
上述研究主要从振荡预防的角度展开, 少有文献讨论S/SSO发生后的处理问题。以往发生的风电场参与的并网系统振荡失稳事故中, 多以切除方式消除S/SSO[14-16]。这种处理方式使得振荡恢复过程中大量有功电源丢失, 不利于振荡恢复后系统的有功平衡。2015年7月发生的新疆哈密直驱风电场事故录波显示, 直驱风电场与弱电网交互产生的S/SSO存在频率耦合[17], S/SSO频率与振荡幅值随风功率波动表现出随时间偏移的特点[18]。文献[19-21]分析了PMSG出力变化对于风电场并网稳定性的影响, 得出减小风电机组出力有助于消除风电场并网系统振荡事故的结论, 为解决直驱风电场并网振荡后抑制提供了新的思路。
本文主要针对直驱风电场在不同运行工况下的并网S/SSO稳定性进行研究, 提出了一种基于直驱风电场功率调整的S/SSO恢复策略。首先, 建立了链式结构直驱风电场导纳模型, 分析了PMSG出力变化对风电场并网系统导纳特性的影响。其次, 基于阻抗分析法, 通过对导纳模型bode图判据分析, 提出了一种基于功率调整的风电场S/SSO抑制策略。最后, 通过MATLAB/Simulink仿真, 验证了S/SSO恢复策略能够维持振荡事故后风电场有功出力水平, 提高了风电场并网系统的可靠性。
1 直驱风电场导纳特性建模
风电场通常包含多台风电机组, 机组之间通过集电线路相互连接后经并网点连接至交流电网。典型的链式结构风电场电气系统如图 1所示。为了便于说明, 这里对每一个链路的风电机组依次进行编号。每个链路中, 与并网点电气距离最近的机组称为首端机组, 与并网点电气距离最远的机组称为末端机组。当有机组停运时, 以投运的机组为准。每台机组的编号记作MN, 其中首位M对应风电机组所处的链路, 末位N对应风电机组在链路内的位置。
由图 1可知, 链式结构的风电场主要由风电机组、包含箱式变压器和中压集电线路的无源网络两部分组成。其中, 风电机组出口处箱式变压器可以采用折算到高压侧的T型电路进行等效, 中压集电线路可以采用单位长度的π型电路进行等效。由此, 一台连接箱式变压器与集电线路的PMSG可以等效为图 2所示的单机-无源网络系统。图 2中, RTL, XTL, YTL分别表示集电线路的电阻、电抗以及对地导纳, YT1, YTM, YT2分别表示箱式变压器低压侧、励磁绕组及变压器高压侧的等值阻抗折算得到的等值导纳, 其表现为纯电气元件, 频域下的导纳特性不随运行方式改变而改变。YPMSG为受多控制环节影响、随运行方式变化的风电机组等值导纳特性。
根据文献[22-23]的研究结果, 建立计及风电机组的双闭环控制环节及锁相环控制作用的PMSG导纳模型, 具体为
| $ \boldsymbol{Y}_{\mathrm{PMSG}}=\left[\begin{array}{ll} Y_{11}(s) & Y_{12}(s) \\ Y_{21}(s) & Y_{22}(s) \end{array}\right] $ | (1) |
式中: Y11(s), Y22(s)——并网逆变器在扰动频率和耦合频率的自导纳;
Y12(s), Y21(s)——扰动频率与耦合频率间的互导纳。
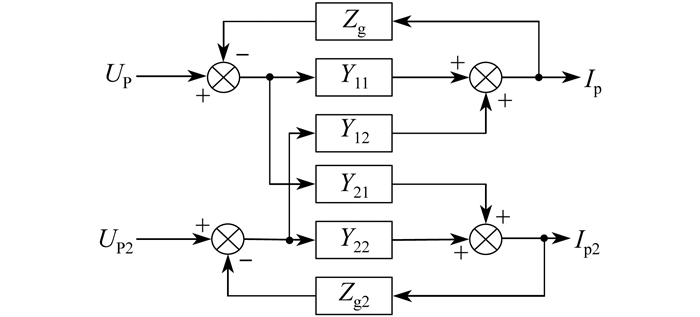
由于并网逆变器的不对称控制结构产生了频率耦合效应, 所以风电机组的阻抗分析过程需同时计及自导纳及互导纳的影响。导纳表达式表现为多输入多输出(Multiple-Input Multiple-Output, MIMO)的2×2阶矩阵, 不具备直观物理意义, 不能采用传统并网稳定分析判据, 而需通过广义奈奎斯特判据来判别系统的稳定性。为简化分析过程, 根据如图 3所示的并网逆变器交流电气量频域关系, 将每台并网逆变器的MIMO序阻抗模型进行简化。其中: Up, Up2, Ip, Ip2为电压及电流在扰动频率及耦合频率的分量。
简化后的单输入单输出(Single-Input Single-Output, SISO)修正序阻抗模型为
| $ Y_{\mathrm{p}}=Y_{11}(s)-\frac{Y_{12}(s) \cdot Z_{\mathrm{g} 2}(s) \cdot Y_{21}(s)}{1+Z_{\mathrm{g} 2}(s) \cdot Y_{22}(s)} $ | (2) |
| $ Y_{\mathrm{n}}=Y_{22}(s)-\frac{Y_{21}(s) \cdot Z_{\mathrm{g}}(s) \cdot Y_{12}(s)}{1+Z_{\mathrm{g}}(s) \cdot Y_{11}(s)} $ | (3) |
式中: Yp, Yn——PMSG的修正正序和负导纳值。
表 1为逆变器端口扰动电压及电流响应分量关系。
表 1
逆变器端口扰动电压及电流响应分量关系
| 名称 | 频率 | 相序 |
| 扰动电压分量 | fp | 正序 |
| fp | 负序 | |
| 扰动电流分量 | fp | 正序 |
| fp | 负序 | |
| 耦合电流分量 | 2f1-fp | 正序 |
| fp+2f1 | 正序 |
由表 1可知, 在次/超同步频段下, 风电场的扰动分量及耦合分量均为正序分量。因此, 对式(2)的修正正序阻抗模型进行分析, 即可得到单台PMSG的并网逆变器导纳特性。
对于包含n台PMSG的一条链路来说, 以第i台机组(i≤n)的接口处为导纳分点, 可以从末端机组开始计算, 1台PMSG与箱式变压器、集电线路串联后再与第2台PMSG并联, 通过递推迭代计算, 可以得到包含i台机组的导纳表达式YPMSG, i_sys, 链路的导纳表达式YL, 完整风电场等值导纳表达式YWF, 为
| $ \begin{aligned} Y_{\mathrm{PMSG}, i_{-} \text {sys }}= & {\left[\left(Y_{\mathrm{PMSG}, i_{-} \text {sys }}+Y_{\mathrm{PMSG}, i_{-} \mathrm{T}}+\frac{Y_{\mathrm{TL}}}{2}\right)+\right.} \\ & \left.\left(R_{\mathrm{TL}}+\mathrm{j} X_{\mathrm{TL}}\right)\right]^{-1}+\frac{Y_{\mathrm{TL}}}{2} \end{aligned} $ | (4) |
| $ Y_{\mathrm{L}}=Y_{\mathrm{PMSG}, n_{-} \text {sys }} $ | (5) |
| $ Y_{\mathrm{WF}}=Y_{\mathrm{L} 1} / / Y_{\mathrm{L} 2} / / Y_{\mathrm{L} 3} / / \cdots / / Y_{\mathrm{L} m} $ | (6) |
2 直驱风电场导纳特性分析
2.1 风电机组出力变化情况
采用导纳灵敏度可以分析出力变化下系统导纳随出力变化的趋势。导纳参数灵敏度定义为
| $ \begin{gathered} D_k(k, s)=\frac{Y_{\mathrm{p}}(k+\Delta k, s)-Y_{\mathrm{p}}(k, s)}{\Delta k} \\ i, j \in\{1, 2\} \end{gathered} $ | (7) |
式中: 下标k——导纳特性相关参数;
Δk——参数单位改变量。
为简化对复数形式导纳表达式的分析, 将导纳参数灵敏度的幅值及相位分别定义为幅值灵敏度Ak(k, Δk, s)及相位灵敏度Pk(k, Δk, s)。其表达式为
| $ A_k(k, \Delta k, s)=\frac{\left|Y_{\mathrm{p}}(k+\Delta k, s)\right|-\left|Y_{\mathrm{p}}(k, s)\right|}{\Delta k} $ | (8) |
| $ P_k(k, \Delta k, s)=\frac{\operatorname{Arg}\left[Y_{\mathrm{p}}(k+\Delta k, s)\right]-\operatorname{Arg}\left[Y_{\mathrm{p}}(k, s)\right]}{\Delta k} $ | (9) |
针对式(2)所示的PMSG正序导纳SISO模型, 在MATLAB/Simulink中建立单机并网仿真模型, 以分析PMSG出力变化对机组等值导纳的影响。直驱风电场并网系统参数如表 2所示。
表 2
直驱风电场并网系统参数
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | |||
| 直流侧电容Cdc/mF | 15 | 解耦系数Kf | 0.1319 | 锁相环Hpll(s)/s | 0.0158+0.99 | 箱式变压器变比k | 35/0.69 | |||
| 滤波电感Lf/mH | 42 | 调制系数Km | 7.73×10-4 | 箱变低压侧阻抗ZT1/Ω | 9.52×10-5+1.57×10-5ω | 单位长度集电海缆电阻R0/(Ω·km-1) | 0.342 1 | |||
| 直流电压Udc/V | 1 300 | 机端交流电压Uvabc/kV | 0.69 | 箱式变压器35 kV侧阻抗ZT2/Ω | 0.367 5+0.076 2ω | 单位长度集电海缆电抗L0/(mH·km-1) | 0.499 | |||
| 直流电压外环Hv(s)/s | 2.23+280.29 | 电流内环Hi(s)/s | 0.48+603.36 | 箱式变压器35 kV侧阻抗ZTM/Ω | 7.6×105+229.33ω | 单位长度集电海缆电容C0/(μF·km-1) | 0.330 5 |
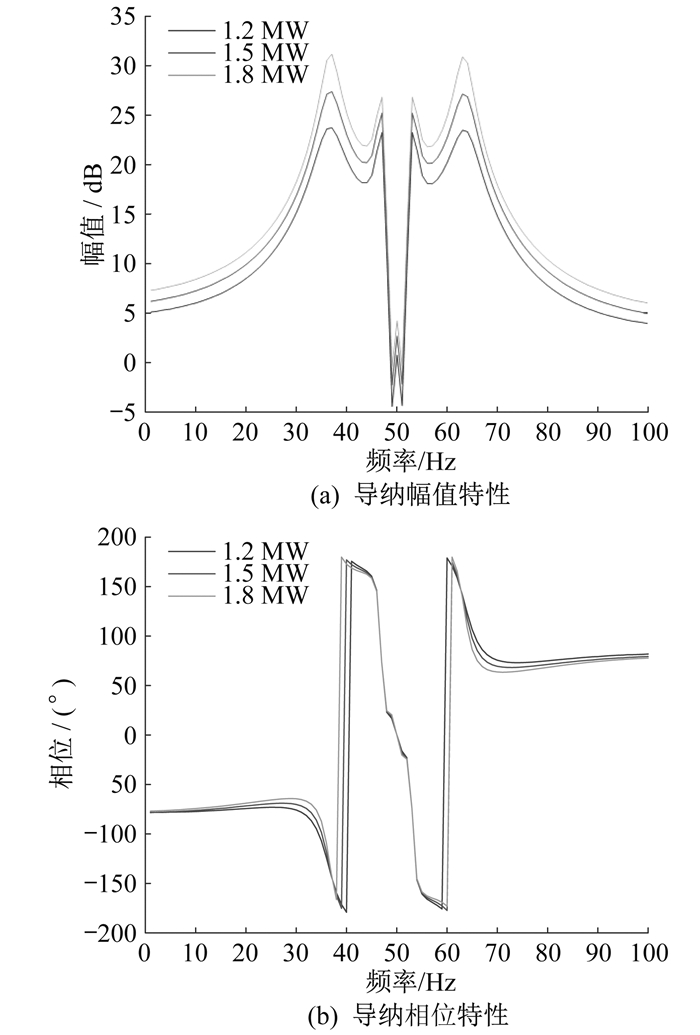
针对PMSG的3种不同出力工况进行仿真, 绘制得到次/超同步频段下的正序导纳频率-幅值图及正序导纳频率-相位图, 具体如图 4所示。
由图 4可知, 在次/超同步频段内, 直驱风电机组恒定存在“负电阻容性”频段, 致使直驱风电机组并网系统随运行方式改变时, 始终存在与感性交流电网发生交互振荡的风险。
由式(8)、式(9)计算结果可知, Ap(1.2, 0.3, s)/Ap(1.5, 0.3, s)≈1, PMSG的导纳特性幅值与风电机组出力大小基本呈现线性变化关系, 而Pp(1.2, 0.3, s)≈Pp(1.5, 0.3, s)≈0, PMSG正序导纳相位受机组出力水平变化的影响可以忽略。
2.2 风电机组电气位置
为了定量表征相同链路内风电机组出力波动对直驱风电场导纳特性的影响, 定义导纳外特性影响因子KPMSG_i(1≤i≤n), 表示同一链路内第i台PMSG出力变化对于风电场导纳外特性的影响。KPMSG_i越大, 调节该机组出力对导纳外特性影响越明显。其表达式为
| $ K_{\mathrm{PMSG}_{-} i}=A_{\mathrm{p}}(\Delta P, s) $ | (10) |
式中: ΔP——PMSG出力变化量。
由式(4)可知, 一个链路的等值导纳与出力相关变量YB可以表示为首端机组-箱式变压器导纳外特性与链式结构剩余风电机组导纳特性的和, 即
| $ Y_{\mathrm{B}}=Y_{\mathrm{PMSG}, n\_\mathrm{T}}+Y_{\mathrm{PMSG}, n-1 \_ \text {sys }} $ | (11) |
联立式(4)中第i项及第i+1项, 可以得到:
| $ \begin{array}{l} \frac{K_{\mathrm{PMSG}_{\_}i+1}}{K_{\mathrm{PMSG}\_i}}=\\ \frac{1}{{\left( {{R_{{\rm{TL}}}} + {\rm{j}}{X_{{\rm{TL}}}}} \right)\left( {{Y_{{\rm{PMSG}}, i - 2\_{\rm{sys }}}} + {Y_{{\rm{PMSG}}, i - 1\_{\rm{T}}}} + \frac{{Y_{{Y_{{\rm{TL}}}}}}}{2}} \right) + 1}} < 1 \end{array} $ | (12) |
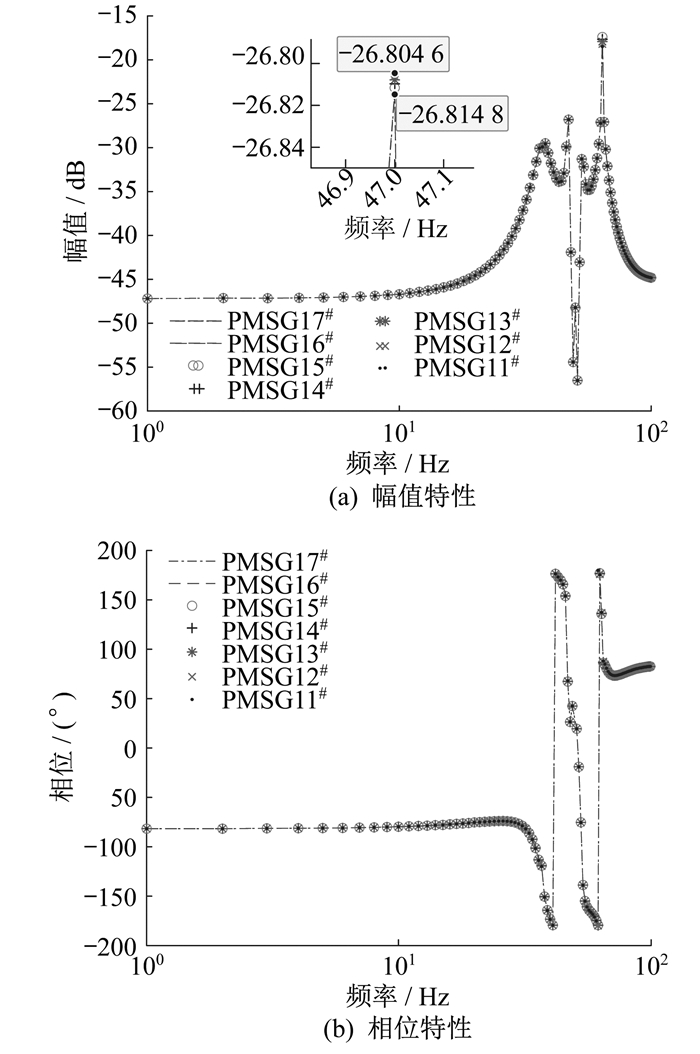
这说明同一链路内, 越靠近并网点的机组出力变化对于链路的等值导纳幅值影响越显著。选取一条有7台风电机组的链路进行分析, 将PMSG11#~PMSG17#的机组出力由1 MW提高至2 MW, 计算得到计及风电场出力差异的链路导纳幅值-相位曲线如图 5所示。
由图 5(a)可以看出, 在相同的机组出力变化量下, 改变首端风电机组出力, 链路导纳幅值大小为-26.804 6 dB, 而改变末端风电机组出力, 链路导纳幅值为-26.814 8 dB。这验证了风电场内一条链路的等值导纳外特性与同一链路内的首端机组出力相关性更大。总之, 风电场内部风电机组的出力变化会对风电场的导纳幅值产生影响, 并且越靠近首端风电机组, 其出力变化对风电场等值导纳的影响更大。
3 风电场并网系统振荡恢复策略
3.1 风电场并网系统稳定性分析
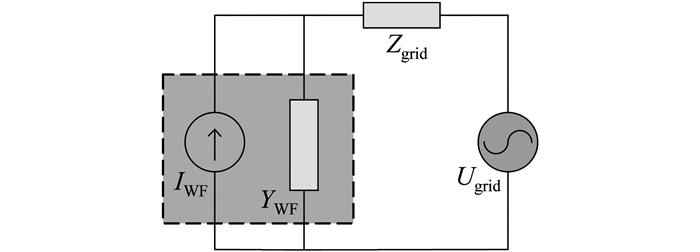
直驱风电场接入交流电网的等效模型如图 6所示。其中, Ugrid为电网电压源, Zgrid为电网等值导纳, IWF为风电场等值功率源, 虚线框内的子系统为等值后的风电场导纳YWF外特性。
根据电路理论可知, 图 6所示系统的稳定性取决于新能源子系统与电网的阻抗比, 计算公式为
| $ G(s)=Z_{\text {grid }}(s) Y_{\mathrm{WF}}(s) $ | (13) |
根据bode图判据, 式(13)可以等价表示为
| $ \left\{\begin{array}{l} \left|Z_{\text {grid }}\right|=\left|Y_{\mathrm{WF}}^{-1}\right| \\ \operatorname{Arg}\left(Z_{\text {grid }}\right)-\operatorname{Arg}\left(Y_{\mathrm{WF}}^{-1}\right)>180 \end{array}\right. $ | (14) |
由此可知, 直驱风电场场-网振荡发生的必要条件为: 风电场等值导纳幅值与交流电网等值导纳幅值相等; 风电场等值导纳相位与交流电网等值导纳相位相差大于180°。
3.2 振荡恢复策略机理分析
直驱风电场与交流电网在运行交互过程中, 交流电网的导纳幅值随负荷波动而改变, 但在次/超同步频段的交流电网的阻抗相位基本保持纯感性不变。由以上分析可知, 当风电机组出力变化时, 其对链式子系统导纳外特性的影响主要体现为导纳幅值的变化。因此, 对直驱风电场并网的S/SSO分析可围绕系统导纳的幅值特性展开。
考虑到单台风电机组的导纳幅值在次/超同步频段内的数值远大于交流电网的导纳幅值。风电场中多台PMSG的功率汇集, 显著降低了风电场侧的输出导纳幅值, 减小了风电场等值阻抗与交流电网产生交互的幅值裕度, 加剧了S/SSO风险。由以上分析可知, 通过对风电机组功率指令进行调整可改变风电机组的导纳幅值, 进而对风电场的整体导纳幅值产生影响, 使直驱风电场与交流电网产生不稳定交互的必要条件被打破。因此, 本文将直驱风电场并网S/SSO后的恢复处理策略概括为一个风电场机组功率优化调整问题, 即振荡发生后, 在保证振荡频率fweak的邻域内, 通过减小风电场出力水平, 使风电场导纳外特性的实部避开交流电网阻抗外特性的幅值, 同时兼顾风电场机组功率调整尽可能小, 能够在解决振荡恢复问题的同时, 保证风电场有功出力水平, 即
| $ \left\{\begin{array}{l} \min P_{\text {loss }} \\ \text { s.t. }\left[\operatorname{abs}\left(Z_{\text {grid }}\right) \neq \operatorname{abs}\left(Y_{\mathrm{WF}}^{-1}\right) \mid f=f_{\text {weak }}\right] \end{array}\right. $ | (15) |
由上面分析可知: 首先, 风电场导纳特性是场内链路导纳的并联, 因此, 对于具有多个链路的直驱风电场, 调节导纳外特性最小链路的机组出力, 对于振荡恢复效果最明显。其次, 链路导纳幅值主要受同一链路内风电机组出力变化的影响, 与不同链路上的风电机组出力波动无关。最后, 同一链路内, 越靠近并网点的机组出力变化对于链路的等值导纳幅值影响越显著,因此, 为满足式(15)中的限制条件, 应优先快速切除直驱风电场中导纳外特性最小链路的首端机组。
对于拥有k条链路的直驱风电场来说, 为了实现振荡过程的快速恢复, 需判断进行功率调整操作的机组数。将直驱风电场中所有链路中的首端机组全部切除, 记为一轮功率调整。为了快速判断每一轮功率调整是否满足式(15)的限制条件, 定义风电场中第j条链式结构首端机组的最大调整导纳幅值量Yadj_max及风电场一轮功率调整的最大调整导纳幅值量Yad_totol_max, 分别为
| $ \left.\begin{array}{l} Y_{\text {adj_max }}= \\ \operatorname{abs}\left\{\begin{array}{l} \frac{Y_{\text {PMSG, } j n \_T}}{\left[1+\left(R_{\mathrm{TL}}+\mathrm{j} X_{\mathrm{TL}}\right)\left(Y_{\text {PMSG, } j n-1 \_ \text {sys }}+Y_{\text {PMSG, } j n \_\mathrm{T}}+\frac{Y_{\mathrm{TL}}}{2}\right)\right]} \\ {\left[1+\left(R_{\mathrm{TL}}+\mathrm{j} X_{\mathrm{TL}}\right)\left(Y_{\mathrm{PMSG}, j n-1 \_ \text {sys }}+\frac{Y_{\mathrm{TL}}}{2}\right)\right]} \end{array}\right. \end{array}\right\} $ | (16) |
| $ Y_{\text {ad_totol_max }}=\sum\limits_{j=1}^k Y_{\text {ad}j\_{\text{max}}} $ | (17) |
取场-网间导纳稳定指标hwg为
| $ h_{\mathrm{wg}}=\operatorname{abs}\left(Z_{\text {grid }}\right) \cdot \operatorname{abs}\left(Y_{\mathrm{WF}}\right) $ | (18) |
根据式(14)的振荡发生必要条件可以看出, 当hwg≠1时, 系统S/SSO不满足风电场等值导纳幅值与交流电网等值导纳幅值相等这一必要条件, 振荡转变为衰减振荡, 系统稳定。由风电场并网S/SSO的既往故障录波数据可知, 由于“负电阻特性”产生的并网系统振荡幅度随时间的增加而增加, 直至达到控制器中的限幅上限, 因此随着时间偏移, 振荡事故对电力系统稳定性的影响增大。为保证功率调整策略实施后直接消除系统振荡, 考虑到振荡后切机过程中风电场导纳数值变化, 以及由于快速傅里叶变换计算过程中因舍入误差而导致的系统误差, 在策略制定时设置系统控制策略的振荡切除阈值为α(α < 1), 保留一定的稳定裕度。即当直驱风电场发生S/SSO时, 降低风电机组输出功率或切除风电机组, 直至满足hwg < α, 系统恢复振荡稳定。
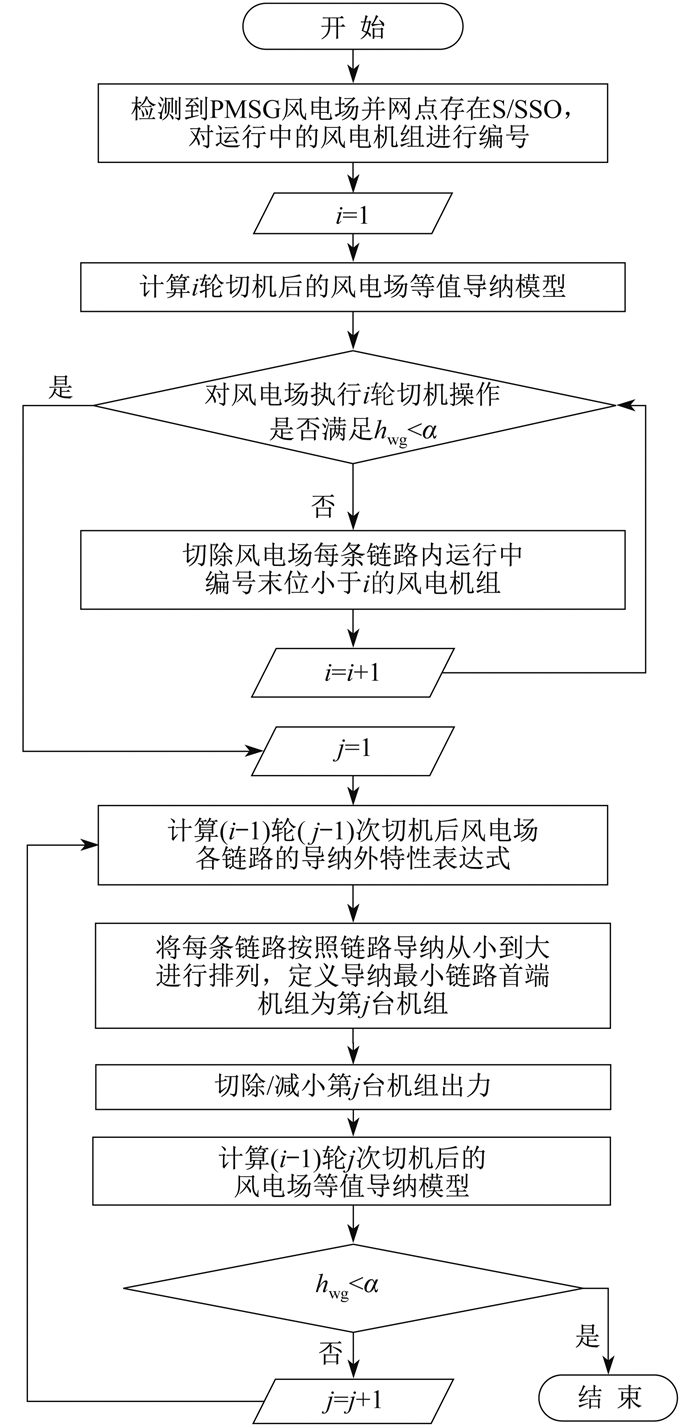
将功率调整过程中的切机过程分为一轮功率调整以及单机功率调整两种类型。为减少振荡事故持续时间, 振荡恢复操作需要进行多轮功率调整操作, 每一轮操作之前通过式(17)中的Yad_totol_max判断: 若满足, 则结束功率调整操作并转为单机功率调整操作; 若不满足, 则切除所有链路中投运的首端机组, 进行下一轮判断, 直至hwg < α。适用于链式结构的直驱风电场振荡恢复策略流程如图 7所示。
3.3 仿真验证
在MATLAB/Simulink中验证本文所提策略的有效性, 算例中振荡切除阈值设为α=0.95。
初始时刻, 风电场内各PMSG的初始出力均为1 MW, 每条链路中投运的机组数分别为5台、4台、3台, 并网系统对应的短路比为6, 系统稳定运行。t=2 s时, 由于风速波动与电网运行方式变化, 短路比减小到2.56, 系统发生S/SSO。直驱风电场与交流电网导纳幅值特性曲线在47.5 Hz处存在交点, 相位相差180°, 即系统满足振荡发生条件。此时, 根据式(11)计算得到扰动频率下风电场各个链路的导纳外特性幅值, 链路1为-22.42 dB, 链路2为-24.35 dB, 链路3为-26.84 dB。链路1的对外总导纳特性最小, 应将该链路的首端机组作为功率调整对象。
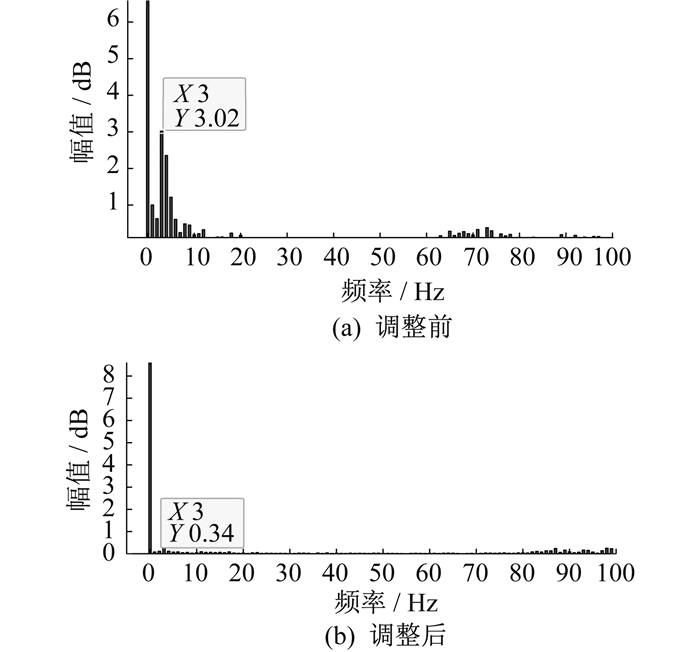
将PMSG11#的出力水平由3 MW降低至1 MW后, 风电场导纳的振荡频率幅值为-23.98 dB, 导纳稳定指标hwg=0.947, 满足振荡稳定条件。功率调整前后的风电场功率频谱分析如图 8所示。
由图 8可以看出, PMSG11#的功率调整后, 振荡消除。因此, 相比风电场切除的振荡恢复方法, 采用本文提出的功率调整控制策略后, 系统振荡满足电力系统稳定要求, 且调整后风电场出力为调整前的91.4%, 大大减少了振荡恢复过程中的有功电源损失。
4 结论
(1) 在次/超同步频段内, PMSG导纳特性呈现为“负电阻容性”频段, 使得直驱风电场并网存在发生S/SSO的风险。对于链式结构的直驱风电场并网, 发生S/SSO的必要条件之一为直驱风电场与交流系统的幅值特性相等。调整PMSG出力或切除相应的风电机组, 有助于直驱风电场并网的S/SSO恢复。
(2) 相比常规的基于风电场切除的S/SSO恢复方法, 本文提出的基于PMSG功率调整的直驱风电场并网S/SSO恢复策略, 有助于快速消除S/SSO, 并在振荡恢复过程中减少电网中的有功电源损失。
参考文献
-
[1]胡家兵, 袁小明, 程时杰. 电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题[J]. 中国电机工程学报, 2019, 39(18): 5457-5467.
-
[2]胡文波, 贾祺, 刘侃, 等. 低运行工况下直驱风电场电流内环主导的次同步振荡特性研究[J]. 太阳能学报, 2022, 43(4): 341-350.
-
[3]徐衍会, 曹宇平. 直驱风机网侧换流器引发次/超同步振荡机理研究[J]. 电网技术, 2018, 42(5): 1556-1564.
-
[4]陈露洁, 徐式蕴, 孙华东, 等. 高比例电力电子电力系统宽频带振荡研究综述[J]. 中国电机工程学报, 2021, 41(7): 2297-2310.
-
[5]王利超, 于永军, 张明远, 等. 直驱风电机组阻抗建模及次同步振荡影响因素分析[J]. 电力工程技术, 2020, 39(1): 170-177.
-
[6]李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一): 宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562.
-
[7]宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4419.
-
[8]LYU J, ZHANG X, CAI X, et al. Harmonic state-space based small signal impedance modeling of a modular multilevel converter with consideration of internal harmonic dynamics[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2134-2148. DOI:10.1109/TPEL.2018.2842682
-
[9]王海宁, 陈燕东, 廖书寒, 等. 弱电网条件下考虑频率耦合的三相并网逆变器简化阻抗建模及宽频带振荡分析[J]. 电源学报, 2021, 19(6): 19-29.
-
[10]张明远, 肖仕武, 田恬. 基于阻抗灵敏度的直驱风电场并网次同步振荡影响因素及参数调整分析[J]. 电网技术, 2018, 42(9): 2768-2777.
-
[11]LIU W, XIE X R, ZHANG X, et al. Frequency-coupling admittance modeling of converter-based wind turbine generators and the control-hardware-in-the-loop validation[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 425-433. DOI:10.1109/TEC.2019.2940076
-
[12]肖仕武, 徐立光. 基于频率耦合阻抗的直驱风电机组次同步振荡关键影响因素分析及抑制措施[J]. 电网技术, 2023, 47(4): 1641-1654.
-
[13]汪海蛟, 何国庆, 刘纯, 等. 计及频率耦合和汇集网络的风电场序阻抗模型等值方法[J]. 电力系统自动化, 2019, 43(15): 87-92.
-
[14]孙华东, 许涛, 郭强, 等. 英国"8·9"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
-
[15]张思彤, 梁纪峰, 马燕峰, 等. 直驱风电场经柔性直流输电并网的宽频振荡特性分析[J]. 电力系统保护与控制, 2022, 50(14): 33-42.
-
[16]CHEN W H, YU X, HAN X Q, et al. Analysis of forced SSOs excited by subsynchronous interharmonics from DPMSG-Based wind farms[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 978-989. DOI:10.1109/TSTE.2020.3028578
-
[17]SHU D, XIE X, RAO H, et al. Sub- and super-synchronous interactions between STATCOMs and weak AC/DC transmissions with series compensations[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7424-7437. DOI:10.1109/TPEL.2017.2769702
-
[18]CHEN W, YU X, HAN X, et al. Analysis of forced SSOs excited by subsynchronous interharmonics from DPMSG-Based wind farms[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 978-989. DOI:10.1109/TSTE.2020.3028578
-
[19]吕佃顺, 许洪华, 马强, 等. 直驱变流器接入弱电网次同步振荡机理分析[J]. 太阳能学报, 2021, 42(5): 423-429.
-
[20]王一珺, 王海风. 直流电压动态时间尺度下大规模直驱风电场振荡稳定性及参数稳定域分析[J]. 中国电机工程学报, 2021, 41(增刊1): 92-107.
-
[21]薛涛, 吕敬, 王凯, 等. 海上全功率风电机组精细化阻抗建模及机网侧耦合分析[J]. 中国电机工程学报, 2022, 42(12): 4303-4319.
-
[22]年珩, 徐韵扬, 陈亮, 等. 并网逆变器频率耦合特性建模及系统稳定性分析[J]. 中国电机工程学报, 2019, 39(5): 1421-1432.
-
[23]武相强, 王赟程, 陈新, 等. 考虑频率耦合效应的三相并网逆变器序阻抗模型及其交互稳定性研究[J]. 中国电机工程学报, 2020, 40(5): 1605-1617.