|
|
|
发布时间: 2024-02-28 |
特约专栏:风电运行与控制技术 |
|
|
|
收稿日期: 2023-03-16
基金项目: 国家自然科学基金(51907115)
中图法分类号: TM315
文献标识码: A
文章编号: 2096-8299(2024)01-0010-07
|
摘要
针对海上风电场疲劳载荷分布不均衡、各机组维护频次不同步而导致运维成本高的问题, 提出了一种考虑疲劳载荷分布的海上风电机组出力优化控制策略。基于风机最小推力系数控制策略有效降低风电场的尾流效应, 以疲劳载荷分布均衡为目标优化各机组的疲劳载荷, 使各机组维护频次同步, 进而降低运维成本。仿真结果表明: 与风机最大功率点跟踪控制策略相比, 所提策略在实现风电场疲劳载荷均衡分布的同时, 使得风电场年发电量提高4.20%。
关键词
风电机组出力; 优化控制; 疲劳载荷分布; 最小推力系数; 海上风电机组
Abstract
To address the problem of unbalanced fatigue load distribution in offshore wind farms and high O&M costs due to the unsynchronized maintenance frequency of each unit, an optimal control strategy for offshore wind turbine output considering fatigue load distribution is proposed, which effectively reduces the wake effect of wind farms based on the minimum thrust coefficient control of wind turbines, optimizes the fatigue load of each unit with the goal of balanced fatigue load distribution, synchronizes the maintenance frequency of each unit, and thus reduces costs. The simulation results show that compared with the maximum power point tracking control strategy, the proposed strategy achieves a balanced distribution of fatigue load on the wind farm while increasing the annual output of the wind farm by 4.20%.
Key words
wind turbine output; optimal control; fatigue load distribution; minimum thrust coefficient; offshore wind turbine
海上风电大规模开发是“双碳”战略实施的重要举措。我国海上可开发风能资源约30亿kW, 开发前景广阔[1]。但海上风电场维护困难[2], 运维费用昂贵, 约为陆上的2~3倍。通过优化海上风电机组的疲劳载荷分布, 降低海上风电场的维护频率, 既能有效降低运维成本, 提升海上风电场的发电效益, 还能提高海上风电场运行的安全稳定性, 意义重大。
目前, 通过优化风电机组的疲劳载荷来降低风电场全生命周期成本的方法主要有3种。第1种对风机某一结构或部件进行疲劳载荷分析。文献[3]以机组损伤维护最频繁的传动系统为研究对象, 在有功控制过程中降低机组传动系统的疲劳载荷。文献[4]以风电机组低速轴和塔筒为研究对象, 采用聚类方法将机组分类, 以各类机组不同结构疲劳载荷最小为目标, 实现最小化机组整体疲劳载荷。第2种对风机整体疲劳程度进行分析与优化。文献[5]以单台风机为例, 验证了风机可通过减载运行有效降低风机的疲劳载荷。文献[6]通过最小化风机的载荷灵敏度之和, 以达到风电场的总疲劳载荷最小化。第3种在第2种的基础上, 考虑了风电场内各台风机疲劳的关联性。文献[7]基于疲劳的累积特性, 提出了利用风电场限值发电期间实现风电场疲劳均匀分布。文献[8]以疲劳均衡性作为优化目标, 提出了以风电场5%~10%的总出力为代价均衡风电场的疲劳载荷分布。文献[9]针对风电场的疲劳分布与出力难以兼顾的问题, 采取了一种折中方法, 同时考虑了风电场的出力和疲劳载荷分布。
上述文献[3-8]提出了多种考虑疲劳载荷的机组出力优化控制策略。但在现有研究中, 风电场的疲劳载荷分布与机组出力两方面难以同时取得较好的优化效果。考虑到海上风电场疲劳载荷均衡分布能够明显降低运维成本, 并有效提升风电场的安全稳定性, 本文提出了一种考虑疲劳载荷分布的海上风电机组出力优化控制策略, 通过最小化风电场的尾流效应, 在均衡风电场疲劳分布的同时, 提高风电场的总有功功率。
1 风电场模型
1.1 风力发电机模型
风机捕获风能功率Pm公式为[10]
| $ P_{\mathrm{m}}=0.5 \rho {\mathsf{π}} R^2 v^3 C_{\mathrm{p}} $ | (1) |
式中: ρ——空气密度;
R——风轮叶片半径;
v——风机的输入风速;
Cp——风能利用系数, 与风机的叶尖速比和桨距角相关。
1.2 风电场尾流模型
Jensen模型[11]是应用最广泛的尾流模型之一, 且精确性较好。具体计算公式为
| $ \begin{gathered} v_{j i}=v_0-v_0\left(1-\sqrt{1-C_{\mathrm{t}}^j}\right) \times \\ \left(\frac{R_i}{R_i+k L_{j i}}\right)^2\left(\frac{S_{\text {overlap }}}{S_i}\right) \end{gathered} $ | (2) |
式中: vji——风速从风机j到风机i的速度衰减量;
v0——风电场的输入风速;
Ctj——风机j推力系数;
Ri——风机i的叶轮半径;
k——尾流衰减常数, 取0.04;
Lji——风机j与风机i之间的纵向距离;
Soverlap——风机j的尾流面积与风机i风轮面积的重叠面积;
Si——风机i的风轮面积。
在风电场中, 风机可能受到多台风机尾流的影响。因此, 采用累积尾流模型[11]计算下游风机的输入风速vi的公式为
| $ v_i=v_0\left\{1-\sqrt{\sum\limits_{j=1}^N\left[1-\left(\frac{v_{j i}}{v_0}\right)\right]^2}\right\} $ | (3) |
式中: N——尾流的数量。
1.3 风电场湍流强度模型
尾流效应不仅会导致下游风机风速损失, 还会增加下游风机区域的湍流强度。湍流强度增加量Ia可以通过Frandsen模型[12]计算。具体公式为
| $ I_{\mathrm{a}}=\frac{1}{1.5+\frac{0.8 d}{D \sqrt{C_{\mathrm{t}}}}} $ | (4) |
式中: d——风机间距;
D——风机叶轮直径;
Ct——风机的推力系数。
风机有效湍流强度Ieff可表示为
| $ I_{\text {eff }}=I_{\mathrm{e}}\left[1+\sum\limits_{j=1}^N \eta_j \exp \left(-\left[\frac{\sigma-\sigma_j}{\sigma_{\omega, j}}\right]^2\right)\right] $ | (5) |
| $ \eta_j=\sqrt{\left(\frac{I_{a, j}}{I_{\mathrm{e}}}\right)^2+1}-1 $ | (6) |
式中: Ie——环境湍流强度;
ηj——尾流j的影响因子;
σ——风电场来风方向;
σj——风机j尾流的方位角;
σω, j——从风机j所看到的产生尾流的风机的特征视角;
Ia, j——风机j处的湍流强度增加量。
1.4 风机疲劳载荷评估模型
考虑到经典疲劳模型难以直接应用到风机的优化控制中, 本文采用了一种简化的风机疲劳载荷评估模型, 以疲劳载荷系数评估风机的疲劳载荷水平[8]。在该模型中, 风机疲劳载荷系数FWT主要来自风机发电导致的工作疲劳FP和风机承受湍流导致的湍流疲劳FI两个部分。具体公式如下:
| $ F_{\mathrm{WT}}=F_{\mathrm{P}}+F_{\mathrm{I}} $ | (7) |
| $ F_{\mathrm{P}}=\frac{\int_0^t P(\tau) \mathrm{d} \tau}{P_{\text {rated }} T_{\text {life }}(1+r)} $ | (8) |
| $ F_{\mathrm{I}}=\eta_{\mathrm{D}} \frac{\int_0^t I_{\text {eff }}(\tau) \mathrm{d} \tau}{T_{\text {life }}(1+r)} $ | (9) |
式中: P(τ)——风机τ时刻的有功功率;
t——时间间隔取值;
Prated——风机的额定功率;
Tlife——风机设计寿命, 取20 a;
r——风机维护修复系数, 取0.5;
ηD——湍流扰动系数;
Ieff(τ)——风机在τ时刻承受的有效湍流。
在风机捕获风能的过程中, 工作疲劳FP和湍流疲劳FI之间存在相关性。为简化疲劳计算, 定义了二者之间的相关系数:
| $ \eta=\frac{F_{\mathrm{I}}}{F_{\mathrm{P}}} $ | (10) |
因此, 风机疲劳载荷系数可通过以下公式计算:
| $ F_{\mathrm{WT}}=(1+\eta) F_{\mathrm{P}}=(1+\eta) \frac{\int_0^t P(\tau) \mathrm{d} \tau}{P_{\text {rated }} T_{\text {life }}(1+r)} $ | (11) |
由式(11)可知, 本文可通过风机的有功功率评估风机的疲劳载荷水平。
2 风电机组出力优化控制策略
2.1 风机控制策略
风机控制策略可以分为最大功率点跟踪(Maximum Power Point Tracking, MPPT)和功率参考跟踪(Power Reference Tracking, PRT)两种控制策略[13]。MPPT控制策略是风机的传统有功功率控制策略。当调度系统对风电场没有功率约束时, 可使用该策略。在该策略中, 风机跟踪其最大风能利用系数, 使风机有功功率最大, 但它会增大风机的推力系数。PRT控制策略是对MPPT控制策略的修改, 风机只需调整风能利用系数偏离其最佳值即可。
2.2 风机最小推力系数控制策略
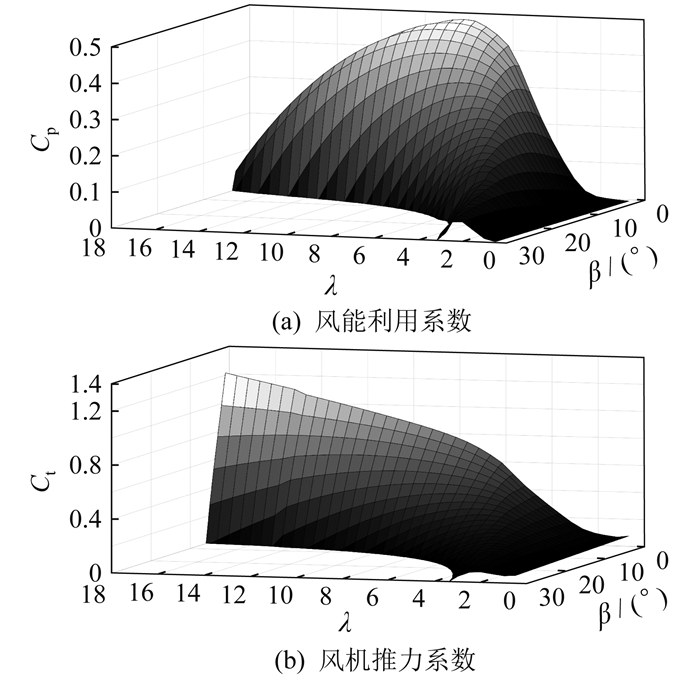
风能利用系数Cp和风机推力系数Ct等高线如图 1所示。
由图 1可知, 风能利用系数Cp的等高线中, 越靠近风机推力系数Ct等高线最大降落方向, 风机的推力系数越小。通过控制风机的叶尖速比λ和桨距角β, 达到风机的推力系数Ct最小的控制策略, 称为最小推力系数控制策略[5]。风机采用最小推力系数控制策略运行, 尾流区风速损失最小, 湍流强度增加量也最小。
风能利用系数和风机推力系数的查找表[14]如图 2所示。本文采用查找表法计算每台风机推力系数Ct。根据式(1)得到每台风机的风能利用系数Cp。在风能利用系数Cp的等高线中, 计算出该值对应的叶尖速比λ和桨矩角β的组合点集, 然后在组合点集中, 求出使得风机推力系数最小的组合点。
2.3 数学模型
在分析分布问题时, 常采用标准差来衡量分布状况, 但考虑即使风机疲劳载荷的标准差很小, 依然需要采用其最大值对应的维护频率对风电场进行维护。因此, 本文采用风电场内风机疲劳载荷的最大值与最小值的比值(定义为均衡度)来衡量风电场的风机疲劳载荷分布情况, 均衡度n单位为倍, 具体表达公式如下:
| $ n=\frac{F_{\max }^{\mathrm{WT}}}{F_{\min }^{\mathrm{WT}}}=\frac{P_{\max }^{\mathrm{WT}}}{P_{\min }^{\mathrm{WT}}} $ | (12) |
式中: FmaxWT, FminWT——风机疲劳载荷的最大值和最小值;
PmaxWT, PminWT——风机有功功率的最大值和最小值。
考虑到尾流效应会影响风电场的发电量, 进一步影响风电场的疲劳载荷分布, 因此本文提出了一种考虑疲劳载荷分布的海上风电机组出力优化控制策略。其在均衡风电场的疲劳载荷分布的同时, 优化风电场有功功率。该策略的优化问题表述如下。
目标函数:
| $ \max \left[\sum\limits_{i=1}^K P_{\mathrm{m}}^i-o_1\left(F_{\max }^{\mathrm{WT}}-n F_{\min }^{\mathrm{WT}}\right)\right], n \geqslant 1 $ | (13) |
式中: K——风电场的风机数量;
Pmi——所提策略中风机i的有功功率;
ο1——惩罚系数。
约束条件:
| $ \omega_{\min } \leqslant \omega \leqslant \omega_{\max } $ | (14) |
| $ \beta_{\min } \leqslant \beta \leqslant \beta_{\max } $ | (15) |
| $ P_i \leqslant P_{\text {rated }} $ | (16) |
| $ \sum\limits_{i=1}^K P_{\mathrm{m}}^i \geqslant \sum\limits_{i=1}^K P_{\mathrm{m}}^{\mathrm{MPPT}-i} $ | (17) |
式中: ω, ωmax, ωmin——转子速度及其上下限;
βmax, βmin——桨距角上下限;
Pi——风机i的有功功率;
PmMPPT-i——风机MPPT策略中风机i的有功功率。
2.4 粒子群优化算法
本文所提策略的优化问题是非线性和非凸的, 因此选择粒子群优化(Particle Swarm Optimization, PSO)算法[15]来获得解决方案。在PSO算法中, 速度和位置根据以下公式更新:
| $ \begin{aligned} v_i^d(k)= & v_i^d(k-1)+c_1 r_1\left[l_{\text {best }_i}^d-x_i^d(k-1)\right]+ \\ & c_2 r_2\left[g_{\text {best }}^d-x_i^d(k-1)\right] \end{aligned} $ | (18) |
| $ x_i^d(k)=x_i^d(k-1)+v_i^d(k) $ | (19) |
式中: vid(k)——第i个粒子在维度d迭代次数k时的速度;
c1, c2——加速度系数;
r1, r2——(0, 1)中均匀分布的随机数;
lbestid——第i个粒子在维度d的局部最佳位置;
xid(k)——第i个粒子在维度d迭代次数k时的位置;
gbestd——粒子在维度d的全局最佳位置。
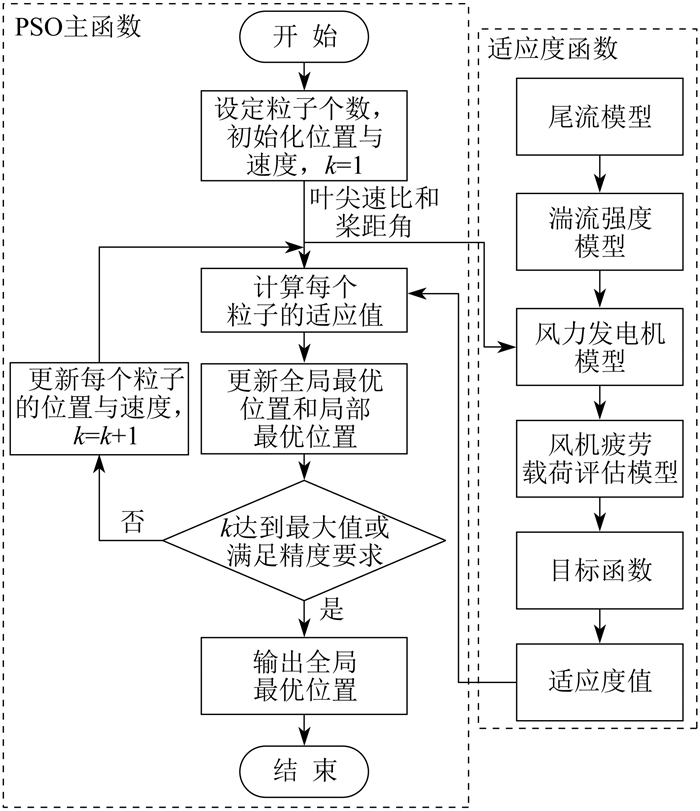
本文采用的PSO算法流程如图 3所示。
图 3中, 适应度函数中风力发电机模型接收PSO主函数的粒子位置值, 即风机的叶尖速比和桨距角, 然后使用尾流模型和湍流强度模型、风力发电机模型、风机疲劳载荷评估模型共同计算适应度值。适应度值反馈给初始粒子位置设置函数和适应度函数对粒子进行评估。最后, 输出使风电场疲劳载荷分布、有功功率最优的叶尖速比和桨距角, 并输出风机的有功功率参考值。
3 案例研究
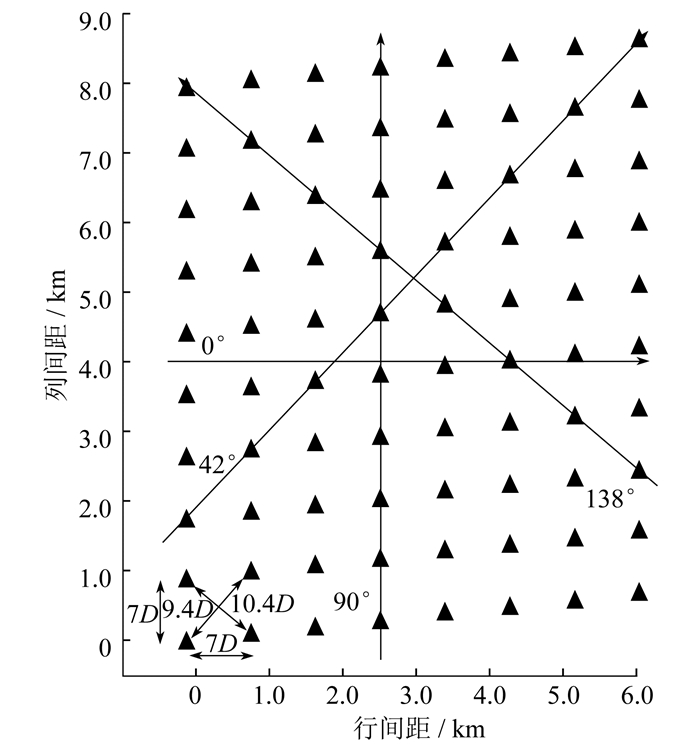
本文以丹麦Horns Rev 1期海上风电场为仿真模型。该风电场由80台风机组成, 风机的间距为风机叶轮直径的7倍, 风电场的排布如图 4所示。图 4中, D为风机叶轮直径, 7D, 9.4D, 10.4D, 表示风机间间距。风机参数[16]如表 1所示。惩罚系数ο1取值1 000, 均衡度n取值1。
表 1
风机参数
| 参数 | 理论值 |
| 切入风速/(m/s) | 3 |
| 额定风速/(m/s) | 11.4 |
| 切出风速/(m/s) | 25 |
| 风机叶轮直径/m | 126 |
| 额定功率/MW | 5 |
| 启动转子速度/(r/min) | 6.9 |
| 额定转子速度/(r/min) | 12.1 |
首先, 设置了两个不同的风况, 来分析本文所提策略和风机MPPT控制策略的效果。风况1:风速9.7 m/s, 来风方向0°, 环境湍流强度0.1。该风速为Horns Rev 1期海上风电场的年平均风速, 且小于风机额定风速。风况2:风速12 m/s, 来风方向0°, 环境湍流强度为0.1。该风速大于风机额定风速, 用来与低于额定风速的风况1对比不同风速对本文所提策略的影响。
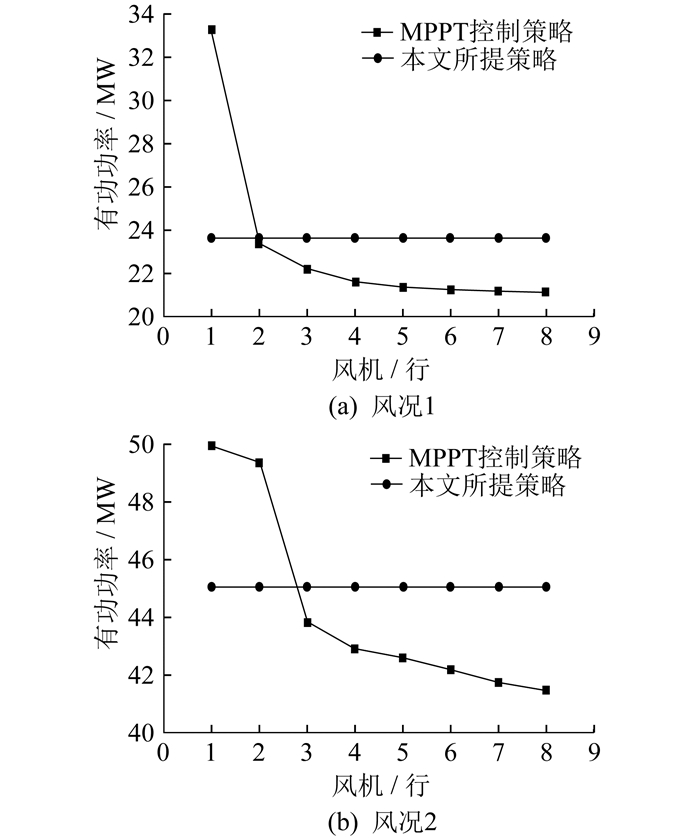
两种策略在风况1和风况2中风电场各行风机有功功率对比如图 5所示。
由图 5可知: 本文所提策略中降低了风电场第1行风机的有功功率, 前排风机减载运行提高了下游风机的有功功率, 同时也降低了第1行风机的疲劳载荷, 下游风机的疲劳载荷也随有功功率的升高而增大; 风况2中风速大于风机的额定风速, 因此MPPT控制策略中第1行风机也相当于进行了减载运行, 这使得第1行风机尾流效应减弱, 为下游风机带来了更多的风能, 如图 5(b)中MPPT控制策略的曲线所示。这就是本文所提策略相比于风况1, 在风况2中提升有功功率效果下降的原因。从第2行开始, MPPT控制策略的曲线趋势风况2与风况1大体保持一致, 因此本文所提策略在不同的风速条件下提升效果基本保持一致。
两种策略在风况1和风况2两种风速条件下风电场总有功功率与均衡度对比如表 2所示。由表 2可知, 相较MPPT控制策略, 本文所提策略在最大均衡风电场疲劳载荷分布的同时, 使得风电场总有功功率在风况1和风况2中分别提升了2.11%和1.72%, 均衡度在风况1和风况2中分别降低了36.31%和45.6%。
表 2
两种策略在两种风况下风电场总有功功率与均衡度对比
| 策略 | 总有功功率/MW | 均衡度/倍 | |||
| 风况1 | 风况2 | 风况1 | 风况2 | ||
| MPPT | 185.1 | 354.1 | 1.57 | 1.21 | |
| 本文所提 | 189.0 | 360.2 | 1.00 | 1.00 | |
上文验证了本文所提策略在不同风速条件下都具有有效性。下文将验证本文所提策略在不同来风风向时的效果, 固定风电场输入风速为9.7 m/s。Horns Rev 1期海上风电场年来风方向的统计数据如表 3所示, 将来风风向采用典型的8扇区统计方式按风向偏差最小的原则进行行列和对角耦合。
表 3
海上风电场年来风方向统计
| 概率 | 来风方向/(°) | 概率 | 来风方向/(°) | |
| 0.251 | 0 | 0.021 | 180 | |
| 0.161 | 42 | 0.109 | 222 | |
| 0.075 | 90 | 0.156 | 270 | |
| 0.019 | 138 | 0.208 | 318 |
不同来风方向时, Horns Rev 1期海上风电场采用MPPT控制策略和本文所提策略运行场内每台风机有功功率分别如图 6所示。同一图中颜色越浅代表数值越大。180°, 222°, 270°, 318°分别与0°, 42°, 90°, 138°相对称, 便不再展示。
由图 6可知, 本文所提策略在不同的来风方向都能有效均衡风电场的有功功率分布, 也能均衡风电场的疲劳载荷分布。
风电场采用两种控制策略的总有功功率与均衡度对比如表 4所示。
表 4
两个策略在不同来风方向下风电场总有功功率与均衡度对比
| 来风方向/(°) | 策略 | 总有功功率/MW | 均衡度/倍 |
| 0 | MPPT | 185.10 | 1.57 |
| 本文所提 | 189.00 | 1.00 | |
| 42 | MPPT | 167.91 | 2.01 |
| 本文所提 | 170.31 | 1.00 | |
| 90 | MPPT | 120.30 | 2.70 |
| 本文所提 | 141.02 | 1.00 | |
| 138 | MPPT | 160.69 | 2.16 |
| 本文所提 | 161.83 | 1.00 |
由表 4可知, 相较MPPT控制策略, 本文所提策略在来风方向为0°, 42°, 90°, 138°下, 总有功功率分别提升了2.11%, 1.43%, 17.22%, 0.71%, 均衡度分别降低了36.31%, 50.25%, 62.96%, 53.70%。由于Horns Rev 1期海上风电场的风机排布设计考虑了尾流效应的影响, 在0°, 42°和138°等主要来风方向, 本文所提策略在发电量提升方面的效率有所下降, 在90°来风方向的发电量提升更加显著; 本文所提策略在任何来风方向下都已做到最大化地均衡风机疲劳载荷分布, 相较于MPPT控制策略, 其在提升发电量和均衡风机疲劳载荷分布两个方面都有明显提升。
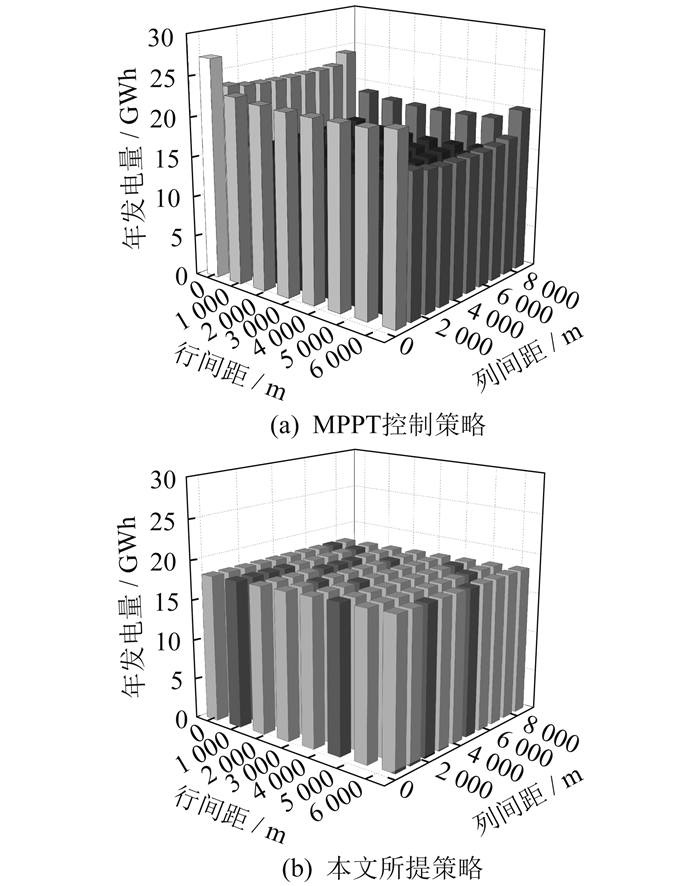
Horns Rev 1期海上风电场全风向时采用MPPT控制策略和本文所提策略仿真运行的年发电量分布如图 7所示。同一图中, 颜色越浅代表数值越大。
由图 7可知, 本文所提策略有效均衡了风电场的疲劳载荷分布。
风电场采用两个策略的年发电量和均衡度对比如表 5所示。由表 5可知: 在均衡疲劳载荷分布方面, 本文所提策略相对于MPPT控制策略降低了45.95%的风电场疲劳均衡度, 优化效果显著; 在年发电量方面, 本文所提策略相比MPPT控制策略提升了58.92 GWh的发电量, 增幅达4.20%。
表 5
风电场在两种策略下年发电量与均衡度对比
| 策略 | 年发电量/GWh | 均衡度/倍 |
| MPPT | 1 401.37 | 1.85 |
| 本文所提 | 1 460.29 | 1.00 |
综上, 本文所提策略是各方面都比较均衡的控制策略, 在有效均衡风电场的疲劳载荷分布的同时, 使得风电场的发电量显著提升。
4 结论
本文提出了一种考虑疲劳载荷分布的海上风电机组出力优化控制策略, 对Horns Rev 1期海上风电场的模型和实际风况数据进行仿真, 将本文所提策略与MPPT控制策略对比分析, 得出结论如下。
(1) 由于Horns Rev 1期海上风电场受布局设计的影响, 风电场发电量在0°, 42°, 90°和138°这4个来风方向分别增加了2.11%, 1.43%, 17.22%和0.71%。这表明本文所提策略在尾流效应越严重的风向中, 提高风电场有功功率的效果越显著。
(2) 与MPPT控制策略相较, 本文所提策略在有效均衡风电场疲劳载荷分布的同时, 使得风电场年发电量提高了4.20%。
参考文献
-
[1]葛畅, 阎洁, 刘永前, 等. 海上风电场运行控制维护关键技术综述[J]. 中国电机工程学报, 2022, 42(12): 4278-4292.
-
[2]万远琛, 王凯, 初岳峰. 海上风电运维的技术现状和发展综述[J]. 船舶工程, 2020, 42(12): 20-25.
-
[3]张斌, 朱春生, 贾鈜崴, 等. 数据驱动的风电机组传动系统疲劳载荷计算与主动抑制研究[J]. 智慧电力, 2023, 51(1): 24-30.
-
[4]刘颖明, 赵哲, 王晓东, 等. 考虑机组疲劳载荷的风电集群有功功率分配方法[J]. 太阳能学报, 2021, 42(5): 430-436.
-
[5]MENG F Z, LIO W H, LIEW J. The effect of minimum thrust coefficient control strategy on power output and loads of a wind farm[J]. Journal of Physics: Conference Series, 2020, 1452(1): 012009. DOI:10.1088/1742-6596/1452/1/012009
-
[6]ZHAO H R, WU Q W, HUANG S J, et al. Fatigue load sensitivity-based optimal active power dispatch for wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1247-1259. DOI:10.1109/TSTE.2017.2673122
-
[7]苏永新, 段斌, 朱广辉, 等. 海上风电场疲劳载荷分布与有功功率统一控制[J]. 电工技术学报, 2015, 30(22): 190-198.
-
[8]ZHAO R Y, DONG D H, LI C L, et al. An improved power control approach for wind turbine fatigue balancing in an offshore wind farm[J]. Energies, 2020, 13(7): 1549-1568. DOI:10.3390/en13071549
-
[9]LIAO H, HU W H, WU X W, et al. Active power dispatch optimization for offshore wind farms considering fatigue distribution[J]. Renewable Energy, 2020, 151: 1173-1185. DOI:10.1016/j.renene.2019.11.132
-
[10]LUO H C, HU Z C, ZHANG H C, et al. Coordinated active power control strategy for deloaded wind turbines to improve regulation performance in AGC[J]. IEEE Transactions on Power Systems, 2019, 34(1): 98-108. DOI:10.1109/TPWRS.2018.2867232
-
[11]张皓, 易侃, 张子良, 等. 基于SCADA数据海上风电场解析尾流模型可靠性与尾流叠加研究[J]. 可再生能源, 2022, 40(10): 1352-1357.
-
[12]FRANDSEN S T. Turbulence and turbulence-generated structural loading in wind turbine clusters[R]. Roskilde, Denmark: Risø National Laboratory, 2007.
-
[13]YAO Q, HU Y, DENG H, et al. Two-degree-of-freedom active power control of megawatt wind turbine considering fatigue load optimization[J]. Renewable Energy, 2020, 162: 2096-2112. DOI:10.1016/j.renene.2020.09.137
-
[14]GRUNNNET J D, SOLTANI M, KNUDSEN T, et al. Aeolus toolbox for dynamics wind farm model, simulation and control[C]//European Wind Energy Conference and Exhibition 2010. Warsaw, Poland, 2010: 3119-3129.
-
[15]ZHANG B H, SOLTANI M, HU W H, et al. Optimized power dispatch in wind farms for power maximizing considering fatigue loads[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 862-871. DOI:10.1109/TSTE.2017.2763939
-
[16]JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R/OL]. [2023-03-02]. https://www.nrel.gov/docs/fy09osti/38060.pdf.