|
|
|
发布时间: 2024-02-28 |
智能设备与检测 |
|
|
|
收稿日期: 2023-05-29
中图法分类号: TM341
文献标识码: A
文章编号: 2096-8299(2024)01-0025-09
|
摘要
为了解决电机振动噪声多、物理域耦合计算耗时长等问题, 提出了基于"FEM+单位力波响应"混合模型的内置式永磁同步电机(IPMSM)振动源快速识别方法。首先, 利用单位力波响应计算电机定子结构关键力波宽频带频响函数特性; 然后, 通过双闭环矢量控制和电磁有限元控制系统-电磁场联合仿真模型, 计算得到电磁力二维傅里叶分解结果, 将其作为模态参与因子获得电机振动加速度频谱特性; 最后, 实验验证了"FEM+单位力波响应"混合模型的准确性。实验结果表明, 对于12槽8极IPMSM, 恒转矩调速时的振动主要是在4阶和8阶固有频率处, 是由4阶力波的14f和8阶力波的fc-3f(其中, f为电机的基频, fc为逆变器的开关频率)分量引起。
关键词
永磁同步电机; 径向电磁力; 单位力波响应; 电磁振动; 响应叠加
Abstract
In order to solve the time-consuming problem of multi-physical domain coupling calculation of motor vibration noise, this paper proposes a fast identification method of interior permanent magnet synchronous motor (IPMSM) vibration source based on "FEM + unit force wave response" hybrid model. Firstly, the unit force wave response is used to calculate the broadband frequency response function characteristics of the key force wave of the stator structure of the motor. Then the FFT results of the electromagnetic force of the control system-electromagnetic field joint simulation model are used as the modal participation factor to obtain the vibration spectrum characteristics of the motor. Finally, the accuracy of the "FEM + unit force wave response" hybrid model is verified by experiments. The results show that for the 12-slot 8-pole IPMSM, the vibration of constant torque speed regulation is mainly at the natural frequencies of 4 and 8, which is caused by the fc-3f component of the 14f of 4 and the force wave of 8 in which, f is the fundamental frequency of the motor, fc is the switching frequency of the inverter.
Key words
permanent magnet synchronous motor; radial electromagnetic force; unit force wave response; electromagnetic vibration; response superposition
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因具有强转矩、高功率密度、宽调速范围和高效率等良好性能, 已被广泛应用于包括机器人、电动汽车等在内的众多现代工业产品中, 而受到广泛关注[1]。然而, 电机振动和噪声会引起PMSM功耗增加、性能降低和寿命缩短等问题, 甚至可能造成突发失磁的严重后果。这就大大限制了其在工业领域的应用范围, 尤其是在关键大功率应用场合。例如, 在车辆行驶过程中存在启动、爬坡和加减速等运行工况, 不同调速方式和运行工况下电机的振动噪声特性不同[1], 会对电机运行的安全可靠性产生影响。研究认为, 低阶径向电磁力波是PMSM振动噪声的主要来源。整数槽多极对数PMSM的主要振动源是零阶径向电磁力波[2-5]。分数槽PMSM, 比如12槽10极PMSM的振动源是2阶径向电磁力波[6-7]。逆变器供电产生的电流谐波主要有5次、7次低频谐波和开关频率处频率为fc±2f和fc±4f(其中, fc为逆变器的开关频率, f为电机的基频)的高频谐波[8-11], 是目前PMSM的主要高频振动噪声源。逆变器供电对整数槽PMSM的影响主要是引入零阶空间力波分量和槽数阶空间力波分量[12]; 对分数槽PMSM的影响主要是引入低阶空间力波分量[13]。
在电机振动噪声的预测方面, 有限元分析通常被认为是最精确的方法[14-15]。然而多物理场联合仿真分析非常耗时, 尤其是在考虑逆变器引入电流谐波的情况下[16]。文献[17-20]提出了PMSM气隙电磁力的快速计算方法, 其中文献[18]提出的定子等效圆环法, 能够快速计算定子结构的振幅。文献[21]提出了一种基于力响应叠加的振动计算方法, 认为选择不含槽区域的定子齿面作为力分解区域, 可以很好地逼近原始气隙力, 能够快速准确地计算出振动响应。文献[22]提出了一种忽略电磁力沿齿面的不均匀的集中力加载方式, 能够有效预测中低频段电磁振动。上述方法均是电机振动噪声的快速计算方法, 但未考虑逆变器引入电流谐波对电机振动产生的影响。
为快速识别内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)的振动噪声源, 提高计算速度, 本文考虑逆变器引入电流谐波影响, 理论分析了IPMSM各阶径向电磁力波的谐波来源。以一台12槽8极IPMSM作为样机, 提出了基于有限元法(Finite Element Method, FEM)和单位力波响应的混合模型IPMSM振动源快速识别方法。其通过软件MATLAB和ANSYS联合搭建控制系统-电磁场联合仿真模型, 利用单位力波响应叠加法来计算各运行工况下振动频谱特性, 并通过实验验证了基于“FEM+单位力波响应”混合模型的IPMSM振动源快速识别方法的准确性。
1 样机电磁力波理论分析
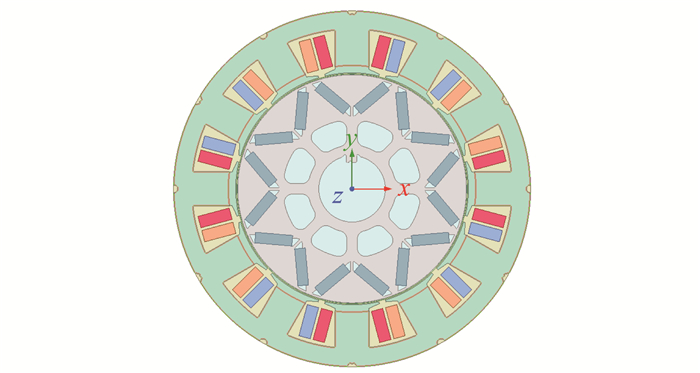
本文采用的12槽8极IPMSM二维电磁有限元模型如图 1所示。
在逆变器供电情况下, 脉宽调制技术产生的电流谐波以及逆变器开关频率会引入新的电磁力波谐波分量, 加剧电机的振动噪声。
忽略铁心磁阻饱和, 引入l次电流谐波的PMSM气隙磁通密度b(θ, t)为
| $ \begin{aligned} & b(\theta, t)=f(\theta, t) {\mathit{\Lambda}}(\theta)=\left[\sum f_\nu(\theta, t)+f_\mu(\theta, t)\right] \times \\ & {\left[{\mathit{\Lambda}}_0+\sum\limits_{k=1}^{\infty} {\mathit{\Lambda}}_k \cos (k z \theta)\right]=} \\ & \sum\limits_l \sum\limits_\nu F_\nu {\mathit{\Lambda}}_0 \cos \left(\nu p \theta-l \omega t-\varphi_\nu\right)+ \\ & \sum\limits_l \sum\limits_\nu \sum\limits_k \frac{F_\nu {\mathit{\Lambda}}_k}{2} \cos \left[(\nu p+k z) \theta-l \omega t-\varphi_\nu\right]+ \\ & \sum\limits_\mu F_\mu {\mathit{\Lambda}}_0 \cos (\mu p \theta-\mu \omega t)+ \\ & \sum\limits_\mu \sum\limits_k \frac{F_\mu {\mathit{\Lambda}}_k}{2} \cos [(\mu p+k z) \theta-\mu \omega t]=\\ & \sum\limits_l \sum\limits_\nu B_{\nu / {\mathit{\Lambda}}_{0 l}} \cos \left(\nu p \theta-l \omega t-\varphi_\nu\right)+ \\ & \sum\limits_l \sum\limits_\nu \sum\limits_k B_{\nu / {\mathit{\Lambda}}_{k l}} \cos \left[(\nu p+k z) \theta-l \omega t-\varphi_\nu\right]+ \\ & \sum\limits_\mu B_{\mu / {\mathit{\Lambda}}_0} \cos (\mu p \theta-\mu \omega t)+ \\ & \sum\limits_\mu \sum\limits_k B_{\mu / {\mathit{\Lambda}}_k} \cos [(\mu p+k z) \theta-\mu \omega t]= \\ & B_{\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}+B_{\mathrm{sl} / {\mathit{\Lambda}}_{k l}}+B_{\mathrm{pm} / {\mathit{\Lambda}}_0}+B_{\mathrm{pm} / {\mathit{\Lambda}}_k}=B_{\mathrm{sl}}+B_{\mathrm{pm}} \end{aligned} $ | (1) |
式中: f(θ, t)——电机气隙磁动势函数;
Λ(θ)——气隙磁导函数;
fν(θ, t)——v次定子绕组谐波磁动势;
v——定子磁场谐波次数, v=1, 5, 7…;
θ——电机机械角度;
fμ(θ, t)——μ次转子永磁体谐波磁动势;
μ——转子磁场谐波次数, μ=1, 3, 5…;
Λ0, Λk——气隙磁导恒定分量和谐波分量幅值, k为气隙磁导谐波次数, k=1, 2, 3…;
z——定子槽数;
l——电流谐波次数, l=1, 5, 7…;
Fν——v次定子绕组谐波磁动势幅值;
p——电机极对数;
ω——基波磁动势角频率;
φν——v次定子电枢谐波初相位;
Fμ——μ次转子永磁体谐波磁动势幅值;
Bν/Λ0l, Bν/Λkl——平均磁导调制、开槽磁导调制引起的定子磁场气隙磁密幅值;
Bμ/Λ0, Bμ/Λk——平均磁导调制、开槽磁导调制引起的转子磁场气隙磁密幅值;
Bsl/Λ0l——平均磁导调制引起的定子磁场气隙磁通密度;
Bsl/Λkl——开槽磁导调制引起的定子磁场气隙磁通密度;
Bpm/Λ0——平均磁导调制引起的转子磁场气隙磁通密度;
Bpm/Λk——开槽磁导调制引起的转子磁场气隙磁通密度;
Bsl——平均和开槽磁导调制引起的定子磁场气隙磁密两者之和;
Bpm——平均和开槽磁导调制引起的转子磁场气隙磁密两者之和。
其中, ν次定子绕组谐波磁动势fν(θ, t)为
| $ f_\nu(\theta, t)=F_\nu \cos \left(\nu p \theta-l \omega t-\varphi_\nu\right) $ | (2) |
μ次转子永磁体谐波磁动势fμ(θ, t)为
| $ f_\mu(\theta, t)=F_\mu \cos (\mu p \theta-\mu \omega t) $ | (3) |
气隙磁导函数Λ(θ)为
| $ {\mathit{\Lambda}}(\theta)={\mathit{\Lambda}}_0+\sum\limits_{k=1}^{\infty} {\mathit{\Lambda}}_k \cos (k z \theta) $ | (4) |
忽略切向磁密, 根据麦克斯韦应力张量法, 单位面积上的径向电磁力波瞬时值pr(θ, t)的解析式为
| $ \begin{gathered} p_r(\theta, t)=\frac{b^2(\theta, t)}{2 \mu_0}=\frac{1}{2 \mu_0}\left(B_{\mathrm{pm}}+B_{\mathrm{sl}}\right)^2= \\ \frac{1}{2 \mu_0} B_{\mathrm{pm}}^2+\frac{1}{\mu_0} B_{\mathrm{pm}} B_{\mathrm{sl}}+\frac{1}{2 \mu_0} B_{\mathrm{sl}}^2=p_{\mathrm{pm}}+p_{\mathrm{pm}-\mathrm{sl}}+p_{\mathrm{sl}} \end{gathered} $ | (5) |
式中: μ0——真空磁导率, 取4π×10-7 H/m;
ppm, ppm-sl, psl——转子磁场产生的、定转子磁场相互作用产生的, 以及定子磁场产生的径向电磁力波。
定转子磁场相互作用产生的径向电磁力波ppm-sl为
| $ \begin{aligned} & p_{\mathrm{pm}-\mathrm{sl}}=\frac{1}{\mu_0} B_{\mathrm{pm}} B_{\mathrm{sl}}=\frac{1}{\mu_0}\left(B_{\mathrm{pm} / {\mathit{\Lambda}}_0}+B_{\mathrm{pm} / {\mathit{\Lambda}}_k}\right) \times \\ & \left(B_{\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}+B_{\mathrm{sl} / {\mathit{\Lambda}}_{k l}}\right)=\frac{1}{\mu_0} B_{\mathrm{pm} / {\mathit{\Lambda}}_0} B_{\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}+ \\ & \frac{1}{\mu_0} B_{\mathrm{pm} / {\mathit{\Lambda}}_k} B_{\mathrm{sl} / {\mathit{\Lambda}}_{k l}}+\frac{1}{\mu_0} B_{\mathrm{pm} / {\mathit{\Lambda}}_0} B_{\mathrm{sl} / {\mathit{\Lambda}}_{k l}}+\frac{1}{\mu_0} B_{\mathrm{pm} / {\mathit{\Lambda}}_k} B_{\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}= \\ & p_{\mathrm{pm} / {\mathit{\Lambda}}_0-\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}+p_{\mathrm{pm} / {\mathit{\Lambda}}_k-\mathrm{sl} / {\mathit{\Lambda}}_{k l}}+p_{\mathrm{pm} / {\mathit{\Lambda}}_0-\mathrm{sl} / {\mathit{\Lambda}}_{k l}}+p_{\mathrm{pm} / {\mathit{\Lambda}}_k-\mathrm{sl} / {\mathit{\Lambda}}_{0 l}} \end{aligned} $ | (6) |
其中, 平均磁导调制引起的转子磁场和定子磁场相互作用所产生的径向电磁力波ppm/Λ0-sl/Λ0l为
| $ \begin{gathered} p_{\mathrm{pm} / {\mathit{\Lambda}}_0-\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}=\frac{1}{2 \mu_0} \sum\limits_\mu \sum\limits_\nu \sum\limits_l B_{\mu / {\mathit{\Lambda}}_0} B_{\nu / {\mathit{\Lambda}}_{0 l}} \times \\ \cos \left[(\mu \pm \nu) p \theta-(\mu \pm l) \omega t-\varphi_\nu\right] \end{gathered} $ | (7) |
开槽磁导调制引起的转子磁场和定子磁场相互作用所产生的径向电磁力波ppm/Λk-sl/Λkl为
| $ \begin{gathered} p_{\mathrm{pm} / A_k-\mathrm{sl} / A_{k l}}=\frac{1}{2 \mu_0} \sum\limits_\mu \sum\limits_\nu \sum\limits_l \sum\limits_k B_{\mu / {\mathit{\Lambda}}_k} B_{\nu / {\mathit{\Lambda}}_{k l}} \times \\ \cos [(\mu p \pm \nu p \pm 2 k z) \theta-(\mu \pm l) \omega t] \end{gathered} $ | (8) |
平均磁导调制引起的转子磁场和开槽磁导调制引起的定子磁场相互作用产生的径向电磁力波ppm/Λ0-sl/Λkl为
| $ \begin{gathered} p_{\mathrm{pm} / {\mathit{\Lambda}}_0-\mathrm{sl} / {\mathit{\Lambda}}_{k l}}=\frac{1}{2 \mu_0} \sum\limits_\mu \sum\limits_\nu \sum\limits_l \sum\limits_k B_{\mu / {\mathit{\Lambda}}_0} B_{\nu / {\mathit{\Lambda}}_{k l}} \times \\ \cos [(\mu p \pm \nu p \pm k z) \theta-(\mu \pm l) \omega t] \end{gathered} $ | (9) |
开槽磁导调制引起的转子磁场和平均磁导调制引起的定子磁场相互作用产生的径向电磁力波ppm/Λk-sl/Λ0l为
| $ \begin{gathered} p_{\mathrm{pm} / {\mathit{\Lambda}}_k-\mathrm{sl} / {\mathit{\Lambda}}_{0 l}}=\frac{1}{2 \mu_0} \sum\limits_\mu \sum\limits_\nu \sum\limits_l \sum\limits_k B_{\mu / {\mathit{\Lambda}}_k} B_{\nu / {\mathit{\Lambda}}_{0 l}} \times \\ \cos [(\mu p \pm \nu p \pm k z) \theta-(\mu \pm l) \omega t] \end{gathered} $ | (10) |
定转子磁场产生的径向电磁力波特征参数如表 1所示。
表 1
定转子磁场产生的径向电磁力波特征参数
| 径向电磁力波 | 力波阶数r | 力波频率fr | 幅值 |
| ppm/Λ0-sl/Λ0l | (μ±ν)p | (μ±l)f | Bμ/Λ0Bν/Λ0l/2μ0 |
| ppm/Λk-sl/Λkl | μp±νp±2kz | (μ±l)f | Bμ/ΛkBν/Λkl/2μ0 |
| ppm/Λ0-sl/Λkl | μp±νp±kz | (μ±l)f | Bμ/Λ0Bν/Λkl/2μ0 |
| ppm/Λk-sl/Λ0l | μp±νp±kz | (μ±l)f | Bμ/ΛkBν/Λ0l/2μ0 |
其中, 电机的基频f=np/60, n表示电机转速。对于本文12槽8极IPMSM, 考虑5次, 7次幅值较大的电流谐波次数, 力波阶数r=4, 8, 16, 20阶时径向电磁力波主要频率分量分别为2f, 4f, 8f, 10f。考虑开关频率附近fc±2f和fc±4f的电流谐波次数, 力波阶数r=4, 8, 16, 20阶时径向电磁力波引入的频率分量分别为fc-f和fc±3f。
2 样机控制系统电磁场联合仿真分析
2.1 样机结构参数
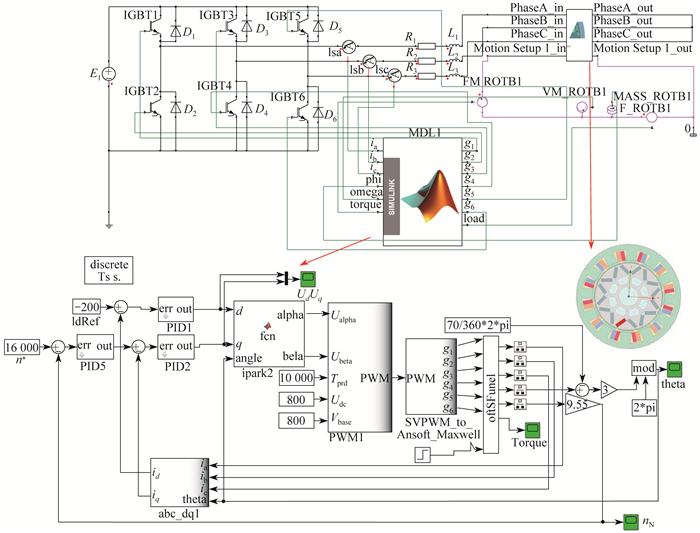
2.2 控制系统电磁场联合仿真模型
2.3 考虑逆变器谐波影响的电磁场仿真分析
为研究不同工况下的电机振动特性, 利用控制系统-电磁场联合仿真模型计算样机额定转速为4 000 r/min, 空载工况和额定负载工况下的电流和电磁力波, 并对计算结果进行傅里叶分析。
图 3为额定负载工况下A相电流二维傅里叶分解图。
由图 3可知, 逆变器电流供电时, 低频处的主要谐波频率为5次、7次谐波, 开关频率处的主要谐波频率为fc±2f, 电机的基频f=266.67 Hz, 与理论分析相符。
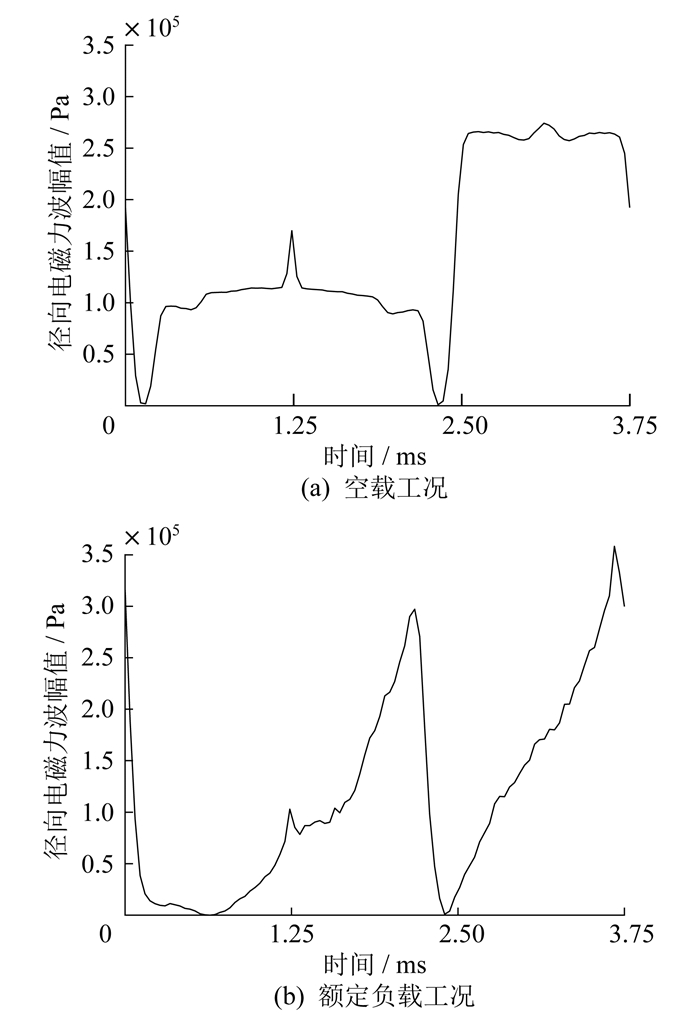
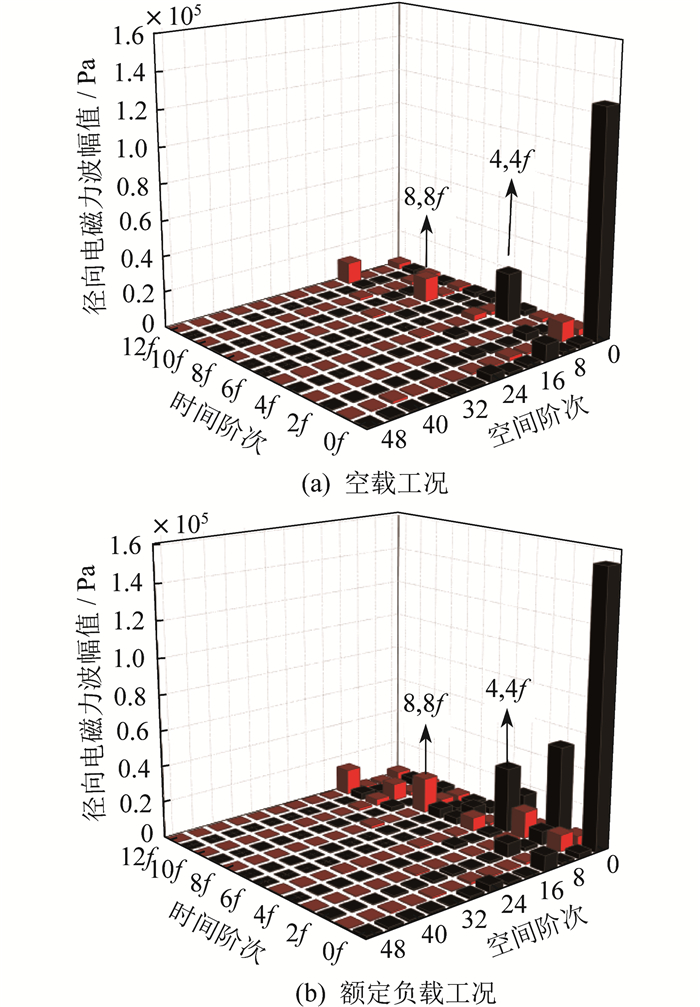
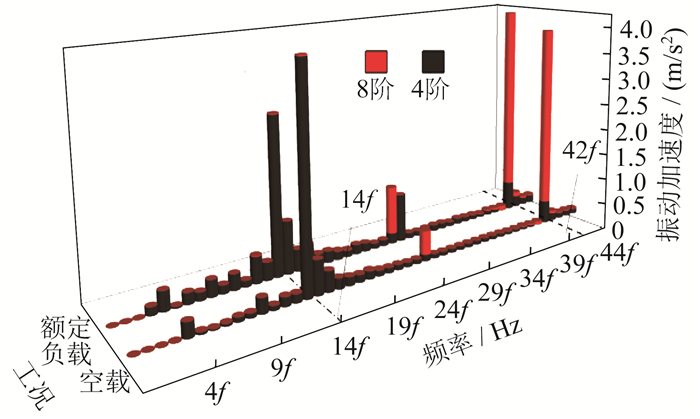
利用ANSYS有限元软件, 计算不同工况下逆变器供电时样机的径向电磁力波并对其进行二维傅里叶分解, 结果分别如图 4和图 5所示。
由图 4可知, 与空载工况相比, 额定负载工况下径向电磁力波谐波较多, 且电磁力波幅值较大。由图 5可知, 空载与额定负载工况下电流的时空分布规律相同, 幅值较大的径向电磁力波的主要阶次为4阶4倍频和8阶8倍频。这与理论分析相符。
3 基于“FEM+单位力波响应”模型的振动频谱特性仿真分析
3.1 样机有限元模态仿真分析
当电机经过加工装配后, 自身的模态频率就是一个定值。研究电机的振动, 首先要计算电机的模态固有频率。当电机力波频率与电机固有频率接近或相等时, 会使电机的振动加剧, 甚至损害电机。因此, 本文通过建立样机定子的三维结构有限元模型, 计算样机定子的各阶振型以及对应的共振频率。
样机定子的三维结构有限元模型如图 6所示, 径向模态是引起电机振动噪声的主要原因。
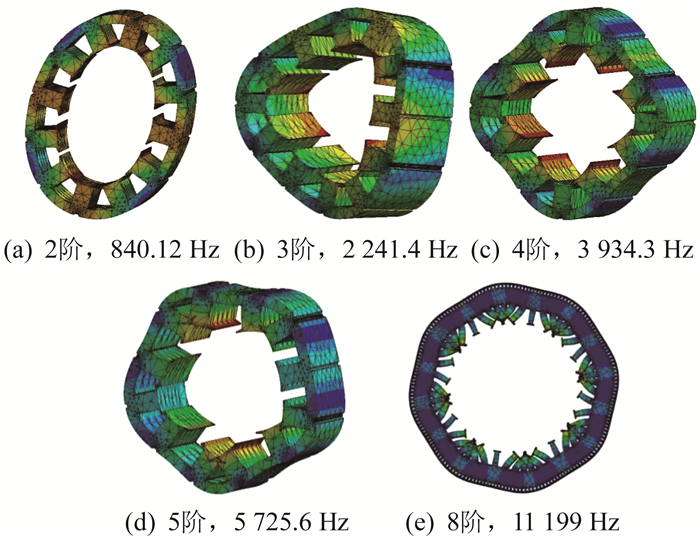
引起本文12槽8极IPMSM振动的有效模态主要是4阶模态和8阶模态, 具体样机定子结构有限元模态如图 7所示。其中, 对样机振动噪声起主要作用的有效模态频率是图 7(c)的4阶固有频率3 934.3 Hz和图 7(e)的8阶固有频率11 199 Hz。
3.2 基于单位力波响应叠加的振动频谱仿真分析
确定模态各阶振型及其对应频率后, 将上文计算得到的电磁力耦合到三维结构场有限元模型, 计算不同工况下的振动加速度。
作用到定子齿上引起电机振动的力波阶数r由电机极槽配合决定, 不会随着电机运行工况的改变而改变, 力波频率和幅值会随着转速和负载的改变而改变。因此, 计算电机结构的振动响应时, 可以先计算单位空间力波响应, 获得电机在整个牵引特性运行范围内的频响函数, 最后, 利用响应叠加方法获得电机某一运行状态下的振动特性, 缩短计算时间, 提高计算效率。
电机线性定子结构r阶单位力波作用时的响应为
| $ X_{\text {unit }, r}(\omega)=H(\omega) p_{\text {unit }, r} $ | (11) |
式中: Xunit, r(ω)——样机定子结构r阶单位力波响应;
H(ω)——样机定子结构的频响函数;
punit, r——r阶单位力波。
根据单位力波响应叠加法获得某一运行工况下电机响应为
| $ X(\omega)=\sum\limits_{r=0}^R X_{\text {unit }, r}(\omega) P_{\mathrm{m} r} $ | (12) |
式中: X(ω)——某一运行工况下的响应;
R——对振动具有较大影响的力波阶数;
Pmr——r阶单位力波在某一运行工况下径向电磁力波二维傅里叶变换后的频谱特性。
Xunit, r(ω)和X(ω)可表示电机定子铁心表面的偏移量、速度或者加速度, 本文取加速度。
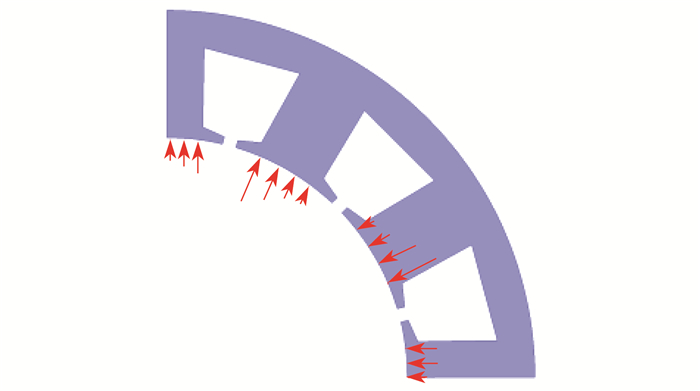
为计算定子结构在各阶单位力波下的振动加速度, 将各阶单位力波分别作用于定子齿上, 激励方式如图 8所示。定子结构各阶单位力波作用下的振动加速度频谱如图 9所示。
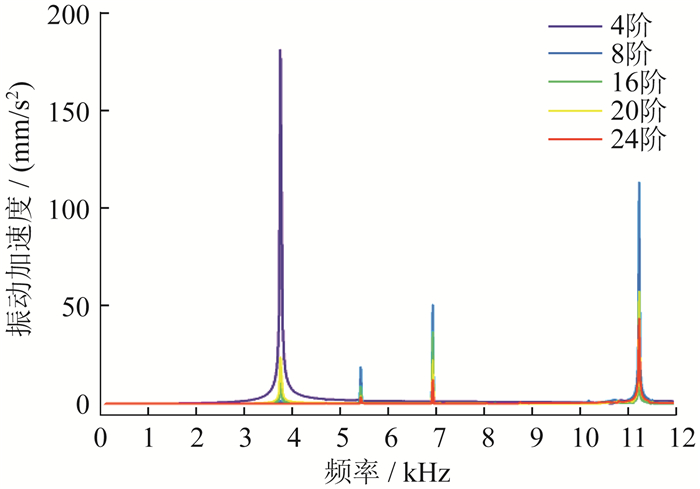
根据单位力波响应叠加法, 获得样机在空载和额定负载不同工况下定子结构振动频谱特性, 如图 10所示。
电机的振动主要是由于时间阶次接近模态频率的空间径向电磁力与固有频率的共振引起的。由图 9和图 10可知: r=16阶、20阶、24阶时力波幅值相对较小; 宽调速范围内引起样机振动的主要是r=4阶和r=8阶径向电磁力波。在恒转矩调速为4 000 r/min时, 样机在3 750 Hz处振幅较大, 此处振动主要由样机的r=4阶电磁力波与4阶固有模态共振引起; 样机在11 200 Hz处振幅较大, 此处振动主要由样机的r=8阶电磁力波与8阶固有模态共振引起。
4 样机实验验证
为了验证本文提出的IPMSM振动源快速识别方法的有效性, 通过实验采集样机振动信号。样机振动实验测试现场如图 11所示。实验采用Simcenter SCADAS XS数据采集与信号分析仪, 用502胶水将三向加速度传感器粘到机壳表面, 通过三向加速度传感器分别输出电机机壳表面的径向(X)、切向(Y)和轴向(Z)的振动加速度信号, 传感器通道及其参数如表 3所示, 驱动器开关频率为12 kHz。
表 3
传感器通道及其参数
| 传感器名称 | 传感器通道 | 方向 | 灵敏度/(MV/g) |
| 加速度传感器 | 1 | X | 20.80 |
| 2 | Y | 20.70 | |
| 3 | Z | 20.45 | |
| 激光转速传感器 | 4 |
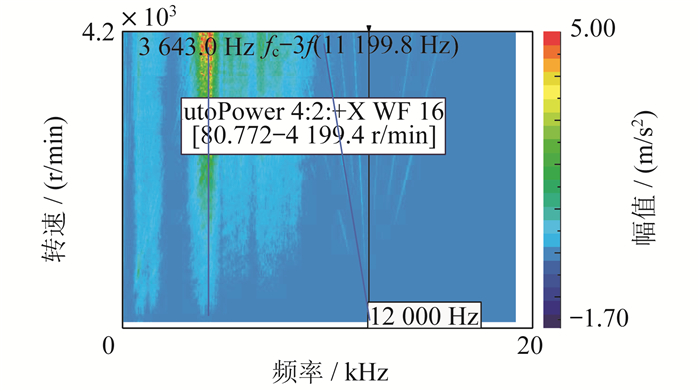
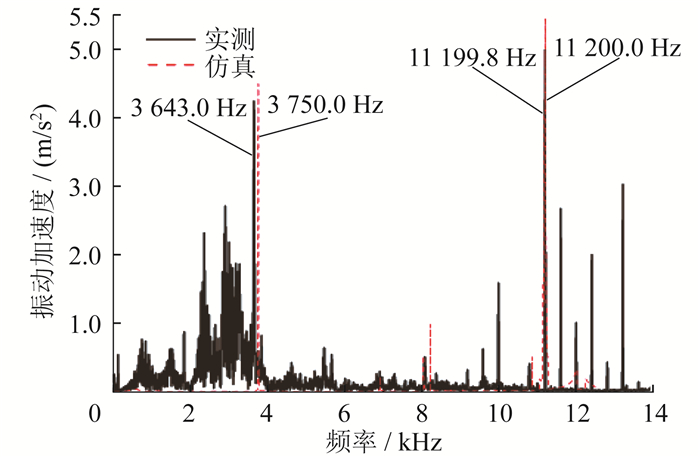
额定负载工况运行下逆变器供电时样机实测振动加速度瀑布图、实测和仿真振动加速度频谱对比, 分别如图 12和图 13所示。
由图 12和图 13可知, 在整个频谱范围内, 样机实测振动加速度在4阶固有频率附近3 643.0 Hz和8阶固有频率附近11 199.8 Hz处振动幅值最大, 与图 9和图 10的仿真分析结果3 750 Hz和11 200 Hz相近。
由此验证了本文提出的IPMSM振动源快速识别方法的准确性, 同时也验证了控制系统-电磁场联合仿真模型的有效性。实测振动加速度幅值略小于仿真结果, 原因在于, 实验所测振动信号为机壳振动数据, 经定子传递到机壳后振动幅值有所减小。
5 结论
本文提出了基于“FEM+单位力波响应”混合模型的IPMSM振动源快速识别方法。以一台12槽8极IPMSM为例, 建立了控制系统-电磁场联合仿真模型, 利用单位力波响应叠加法计算各工况振动频谱特性, 快速识别电机不同运行工况下的振动源, 并通过实验验证了本文方法的正确性。所得结论如下。
(1) 逆变器供电时样机振动源的增加主要分布在开关频率附近, 尤其是在开关频率的fc-3f处。本文8阶的固有频率刚好在开关频率附近, 电磁力波分量与电机固有频率接近, 使得开关频率处的振动加剧。
(2) 本文通过实验验证了所提“FEM+单位力波响应”振动源快速识别方法的准确性。样机在4阶固有频率附近3 643.0 Hz (14f)和8阶固有频率附近11 199.8 Hz (fc-3f)处振动幅值较大。这主要是由逆变器引入的电流谐波产生。样机的振动测试信号与联合仿真计算的振动加速度规律基本一致, 也验证了联合仿真模型的有效性。
参考文献
-
[1]GAO L Y, ZHENG H B, ZENG L B, et al. Evaluation method of noise and vibration used in permanent magnet synchronous motor in electric vehicle[C]//2019 IEEE Transportation Electrification Conference and Expo (ITEC). Detroit, MI, USA: IEEE, 2019: 1-4.
-
[2]MCDEVITT T E, CAMPBELL R L, JENKINS D M. An investigation of induction motor zeroth-order magnetic stresses vibration and sound radiation[J]. IEEE Transactions on Magnetics, 2004, 40(2): 774-777. DOI:10.1109/TMAG.2004.824772
-
[3]VALAVI M, BESNERAIS J L, NYSVEEN A. An investigation of zero-order radial magnetic forces in low-speed surface-mounted permanent magnet machines[J]. IEEE Transactions on Magnetics, 2016, 52(8): 7206-7216.
-
[4]LI X H, HUANG S R, ZHANG Q, et al. Electromagnetic noise assessment for EV's PM driving machines[C]//International Conference on Electrical Machines and Systems (ICEMS). Hangzhou, China: IEEE, 2014: 1552-1555.
-
[5]HOFMANN A, QI F, LANGE T, et al. The breathing mode-shape 0: is it the main acoustic issue in the PMSMs of today's electric vehicles? [C]//International Conference on Electrical Machines and Systems (ICEMS). Hangzhou, China: IEEE, 2014: 3067-3073.
-
[6]KIM D, PARK M, SIM J, et al. Advancedmethod of selecting number of poles and slots for low-frequency vibration reduction of traction motor for elevator[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(4): 1554-1562. DOI:10.1109/TMECH.2017.2695059
-
[7]YANG H D, CHEN Y S. Influence ofradial force harmonics with low mode number on electromagnetic vibration of PMSM[J]. IEEE Transaction on Energy Conversion, 2014, 29(1): 38-45. DOI:10.1109/TEC.2013.2290304
-
[8]左曙光, 刘晓璇, 于明湖, 等. 永磁同步电机电磁振动数值预测与分析[J]. 电工技术学报, 2017, 32(1): 159-167.
-
[9]PELLEREY P, LANFRANCHI V, FRIEDRICH G. Coupled numerical simulation between electromagnetic and structural models[J]. IEEE Transactions on Magnetics, 2012, 48(2): 983-986. DOI:10.1109/TMAG.2011.2175714
-
[10]唐任远, 宋志环, 于慎波, 等. 变频器供电对永磁电机振动噪声源的影响研究[J]. 电机与控制学报, 2010, 14(3): 12-17.
-
[11]肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
-
[12]LIN F, ZUO S G, DENG W Z, et al. Modeling andanalysis of electromagnetic force vibration and noise in permanent-magnet synchronous motor considering current harmonics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7455-7466. DOI:10.1109/TIE.2016.2593683
-
[13]林福, 左曙光, 毛钰, 等. 考虑电流谐波的永磁同步电机电磁振动和噪声半解析模型[J]. 电工技术学报, 2017, 32(9): 24-31.
-
[14]ZUO S G, LIN F, WU X D. Noise analysis, calculation, and reduction of external rotor permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6204-6212. DOI:10.1109/TIE.2015.2426135
-
[15]代颖, 崔淑梅, 张千帆. 车用异步电机的电磁振动/噪声分析[J]. 中国电机工程学报, 2012, 32(33): 89-97.
-
[16]郑江, 代颖, 石坚. 车用永磁同步电机的电磁噪声特性[J]. 电工技术学报, 2016, 31(增刊1): 53-59.
-
[17]LIANG W Y, LUK P C K, FEI W Z. Analytical investigation of side band electromagnetic vibration in integral-slot PMSM drive with SVPWM technique[J]. IEEE Transactions Power Electronics, 2017, 32(6): 4785-4795. DOI:10.1109/TPEL.2016.2602944
-
[18]邢泽智, 王秀和, 赵文良, 等. 表贴式永磁同步电机电磁激振力波计算与定子振动特性分析[J]. 中国电机工程学报, 2021, 41(14): 5004-5013.
-
[19]LYU Y J, CHENG S W, WANG D, et al. A fast method for calculating the air-gap flux and electromagnetic force distribution in surface permanent magnet motors[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia). Nanjing, China: IEEE, 2020: 1973-1977.
-
[20]LEE S H, YANG I J, KIM W H, et al. Electromagnetic vibration-prediction process in interior permanent magnet synchronous motors using an air gap relative permeance formula[J]. IEEE Access, 2021, 9: 29270-29278. DOI:10.1109/ACCESS.2021.3055864
-
[21]BOESING M, SCHOENEN T, KASPER K A, et al. Vibrationsynthesis for electrical machines based on force response superposition[J]. IEEE Transactions on Magnetics, 2010, 46(8): 2986-2989.
-
[22]左曙光, 刘晓璇, 于明湖, 等. 永磁同步电机电磁振动数值预测与分析[J]. 电工技术学报, 2017, 32(1): 159-167.