|
|
|
发布时间: 2024-02-28 |
智能设备与检测 |
|
|
|
收稿日期: 2023-11-15
中图法分类号: TH113.1;TM303
文献标识码: A
文章编号: 2096-8299(2024)01-0034-05
|
摘要
对电机模态固有频率的精确计算及准确分析是电机低噪声驱动设计的一个重要环节。由于用于电动汽车的永磁同步电机(PMSM)属于小型电机, 机壳和端盖等装置对振动噪声的影响不容忽略, 因此对不同电机结构部件以及耦合系统固有频率进行计算分析具有重要意义。基于一台12槽8极PMSM, 利用有限元软件, 考虑了铁心材料的各向异性、弹性模量、浸漆、机壳和端盖连接方式等影响, 精确建立了定子铁心结构的计算模型, 并用锤击法模态实验验证了有限元仿真模型的精确性。
关键词
永磁同步电机; 有限元法; 机壳和端盖; 整机模态; 锤击法模态实验
Abstract
The precise calculation and accurate analysis of the natural frequencies of motor modes are crucial for the design of low-noise motor drives. Permanent magnet synchronous motors (PMSM) used in electric vehicles are considered small-scale motors, and the influence of components such as the casing and end caps on vibration noise cannot be overlooked. Therefore, it is of great significance to accurately calculate and analyze the natural frequencies of different motor structural components and coupled systems. Based on a 12-slot 8-pole PMSM, finite element software is utilized to consider the effects of core material anisotropy, elastic modulus, impregnation, and casing-end cap connection methods. A precise computational model of the stator core structure is established, and the accuracy of the finite element simulation model are verified using modal experiments.
Key words
permanent magnet synchronous motor; finite element method; shell and cover; whole machine mode; hammer method experimental mode
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有功率密度高、量轻、小型等优点, 是当前最主流的电动汽车驱动电机。模态分析是PMSM结构振动噪声特性分析的基础。早期电机模态分析主要运用机电类比法, 包括单环型机电类比法和双环型机电类比法[1]。文献[2]用解析法分析了定子齿、绕组、机壳等结构对电机固有频率的影响。为获得更精确的模态分析结果, 目前有限元分析软件与实验相结合的方法是模态分析的主要方法。电机结构复杂, 绕组、机壳、端盖、绕组浸漆、材料各向异性及不同材料接触面设置等都会对准确分析电机结构模态产生影响。文献[3]采用有限元和实验相结合的方法, 从简单的圆环结构开始, 分析了电机结构中各种不对称现象对电机结构固有模态的影响。文献[4]采用有限元法, 分析了定子铁心以及电机部件低阶次的固有频率, 认为绕组质量对于定子结构固有频率的影响大于绕组刚度的影响。文献[5]认为, 端盖主要影响定子低阶模态固有频率, 对于高阶模态影响很小。文献[6]采用有限元法对车用异步电机进行模态分析。文献[7]分析了绕组浸漆前后定子固有频率的变化以及端部绕组对定子固有频率的影响, 发现绕组端部长度影响定子的固有频率, 浸漆会提高低阶径向模态固有频率。
目前, 对于PMSM模态参数的研究多为对电机定子铁心的研究。实际上, 对小型电机来说, 机壳、端盖等装置对振动噪声的影响不能忽略。因此, 基于上述研究基础, 首先, 本文对一台12槽8极PMSM不同定子结构的各阶模态参数进行了分析研究; 其次, 在有限元建模时, 考虑了绕组机壳和端盖材料的各向异性以及各部分之间的连接方式, 得出了绕组结构、机壳和端盖对定子铁心固有频率的影响; 最后, 通过锤击法模态实验, 验证了仿真模型的精确性。
1 模态分析理论
n个单独零部件结构的自由振动微分方程为
| $ \left\{\begin{array}{c} m_1 \ddot{x}_1+c_1 \dot{x}_1+k_1 x_1=0 \\ m_2 \ddot{x}_2+c_2 \dot{x}_2+k_2 x_2=0 \\ \vdots \\ m_n \ddot{x}_n+c_n \dot{x}_n+k_n x_n=0 \end{array}\right. $ | (1) |
式中: m1, m2, …, mn——零部件质量属性;
c1, c2, …, cn——零部件阻尼系数;
k1, k2, …, kn——零部件刚度系数;
x——振动位移;
ẋn, ẍn——x的一阶导数和二阶导数。
设置系统自由度为n的多自由度振动系统, 则系统矩阵形式的运动微分方程为
| $ \mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{C\dot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}} $ | (2) |
式中: M——质量矩阵;
C——阻尼矩阵;
K——刚度矩阵;
F——节点力矢量;
u——节点位移矢量。
在自由振动情况下, 运动微分方程可以转换为求系统特征值问题, 而系统特征值和特征向量则可以反映出结构的模态参数。根据无阻尼、自由振动假设, 令式(2)中F={0}, 时间导数用ω代替(ω为角频率), 则有
| $ \left(\boldsymbol{K}-\omega^2 \boldsymbol{M}\right) \boldsymbol{u}=\{0\} $ | (3) |
能满足式(3)中u的各种元素取值不是唯一的, 但各元素间的相对比值是固定不变的, 即系统各阶模态的形状是唯一的, 但是大小可以放大或缩小。根据线性方程组理论, 则非零解的充分必要条件K-ω2M=0, 得到m个特征根ωr(r=1, 2, 3, …, m)和对应的特征向量ur(r=1, 2, 3, …, m), ωr和ur分别为电机的固有频率和对应的振型[8-9]。
目前, 模态分析法主要是指有限元法和实验模态分析法。有限元法(Finite Element Method, FEM)能够考虑结构的不规则性, 计算精度较高。近年来计算机技术的飞速发展, 使得利用有限元法进行工程仿真分析成为一种潮流。实验模态分析法利用模态测试实验平台, 获得样机的固有频率、模态阻尼、模态振型等模态参数, 从而估算电机整个调速范围内的振动特性, 优化有限元模型, 验证电机结构设计的合理性, 优化电机结构设计的有限元设计方案, 并可以进行电机结构的故障分析。
2 三维有限元法仿真实验
为了提高对电机模态参数预测精度, 本文采用了三维有限元法进行仿真, 并充分考虑了电机定子结构的复杂性以及各种材料的各向异性。本文分别建立了样机的定子铁心、定子铁心加绕组、定子铁心加机壳和端盖(以下简称机壳加端盖)3种结构的三维有限元仿真模型, 分析了绕组结构、机壳和端盖对电机结构模态固有频率的影响。
在小型PMSM中, 机壳和端盖等装置对振动噪声的影响不能忽略。同时, 绕组、机壳和端盖对电机模态频率的影响一直是电机模态分析中的一个难点。原因在于: 首先, 各结构形状复杂, 建立等效模型难度大; 其次, 绕组是由导线、绝缘和空气隙等组成的混合结构, 加上绕组浸漆后机壳和端盖的耦合, 是一个复杂的复合材料体, 其密度、弹性模量和泊松比等模态仿真参数均难以确定。
在本文中, 用体积相等的铜条代替定子绕组, 环状同心圆代替绕组端部, 并假设各部分紧密连接且实际质量相等。绕组密度与质量之商等效绕组体积, 根据绝缘材料、气隙比例及槽满率等效弹性模量, 建立定子铁心结构及其绕组的三维模态仿真模型。本文研究的电机结构参数及有限元法分析的材料力学参数分别如表 1和表 2所示。其中, 表 1中的绕组节距为5。
表 1
12槽8极PMSM结构参数
| 结构参数 | 数值 |
| 定子铁心外径 | 67.00 |
| 定子铁心内径 | 43.75 |
| 气隙长度 | 0.75 |
| 转子铁心外径 | 43.00 |
| 转子铁心内径 | 12.50 |
| 定子铁心长度 | 60.00 |
| 转子铁心长度 | 60.00 |
表 2
有限元法分析的材料力学参数
| 结构部件 | 密度/(kg/m3) | 弹性模量/Pa |
| 定子铁心 | 7 410 | EX=EY=2.058×1011 EZ=1.5×1011 |
| 定子绕组 | 4 382 | EX=EY=8.5×1010 EZ=1.2×1010 |
| 机壳和端盖 | 2 770 | EX=EY=EZ=7.1×1010 |
| 结构部件 | 剪切模量/Pa | 泊松比 |
| 定子铁心 | GXZ=GYZ=7.3×1010 GXY=8.0×1010 |
0.30 |
| 定子绕组 | GXZ=GYZ=5.4×109 GXY=4.6×109 |
0.30 |
| 机壳和端盖 | GXY=GXZ=GYZ=2.7×1010 | 0.33 |
通过以上假设和等效, 考虑定子铁心建模时叠片铁心的影响, 可以分别得到样机不同定子结构的有限元等效模型。具体如图 1所示。
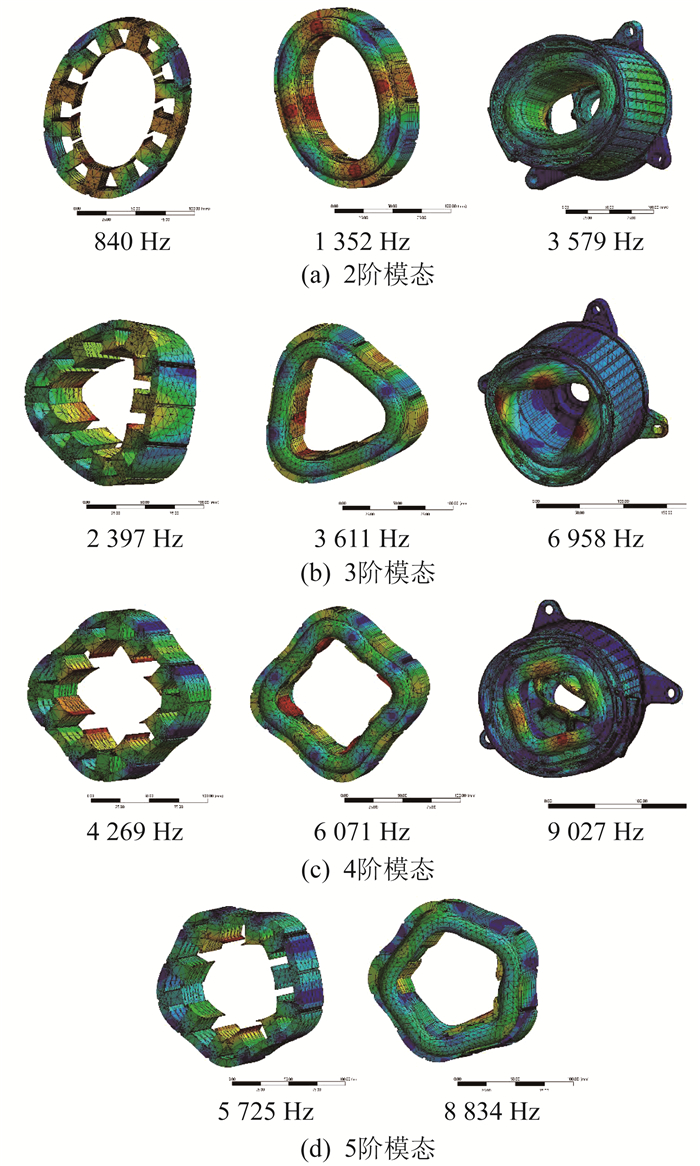
将上述模型导入ANSYS中Workbench模块, 对不同电机结构的有限元模型进行自由模态分析, 得出定子铁心和机壳加端盖结构有限元模型在自由无约束条件下的固有频率和相应振型。定子结构不同模态的有限元振型如图 2所示。其中, 各图形从左到右分别表示定子铁心、定子铁心加绕组、机壳加端盖3种结构的振型、固有频率和位移幅度, 图形颜色代表位移幅度的大小。
由图 2可知: 定子铁心和定子铁心加绕组结构2阶模态振型为径向振动和椭圆振动的组合模态, 固有频率分别为840 Hz和1 352 Hz, 振动位移最大值为27.43 mm和19.77 mm, 最小值为10.10 mm和5.99 mm; 3阶模态振型为轴向平面振动和径向平面振动的组合模态, 固有频率分别为2 397 Hz和3 611 Hz, 振动位移最大值为39.80 mm和23.40 mm, 最小值为0 mm。4阶模态振型为轴向和径向平面振动的组合模态, 固有频率分别为4 269 Hz和6 071 Hz, 振动位移最大值为42.29 mm和28.56 mm, 最小值为1.00 mm和0 mm。5阶模态振型为轴向和径向平面振动的组合模态, 固有频率分别为5 725 Hz和8 834 Hz, 振动位移最大值为39.81 mm和42.21 mm, 最小值为0.44 mm和0.14 mm。机壳加端盖模态振型为各种程度的椭圆、径向、轴向振动的组合, 具有明显耦合现象; 2阶模态振型的固有频率为3 579 Hz, 振动位移最大值为29.10 mm, 最小值为1.00 mm; 3阶模态振型的固有频率为6 958 Hz, 振动位移最大值为63.30 mm, 最小值为0 mm; 4阶模态振型的固有频率为9 027 Hz, 振动位移最大值为64.00 mm, 最小值为0 mm。
由有限元仿真结果可知, 定子铁心加绕组后, 由于刚度的大幅上升, 使得其部件的固有频率明显提高, 有利于避开二倍基波频率的电磁激振力的振动频率。机壳端部与定子端盖联结, 相当于对机壳端部施加了一定的径向约束力, 在一定程度上提高了合成结构轴向两端的刚度, 提升了电机定子结构的固有频率。
3 锤击法模态实验
为验证理论分析及有限元模型的正确性, 本文采用“Simcenter SCADAS XS”数据采集与信号分析系统对样机结构进行锤击法模态实验, 并采用LMS公司开发的test.lab平台后处理软件进行模态分析。本实验尽量让被测设备模拟自由状态。将被测物体用柔软、有弹性的绳子悬吊起来, 悬挂绳足够软、长, 悬挂绳的固有频率足够低, 以保证刚体共振频率远低于一阶弹性体共振频率, 模拟近似自由状态。质量很轻、阻尼很小的结构对悬挂绳的柔软程度敏感, 由于本文定子铁心、定子铁心加绕组结构及机壳加端盖的质量较大, 因此可以忽略悬挂绳对模态频率测试结果的影响。图 3为被测样机照片结构。图 4为现场测试照片。
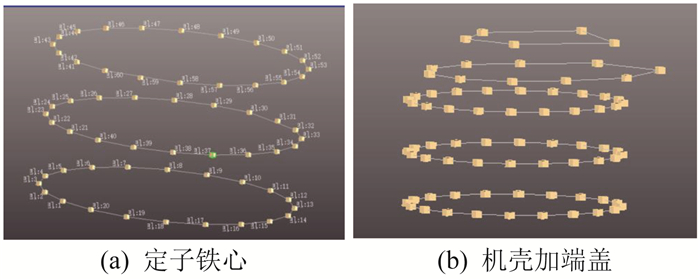
在样机结构上等间隔取点, 分别对这些点施加激励, 响应参考点固定, 如果在某个点激励后测得的响应很小, 则说明激励点位于节点位置, 需要重新更换激励点, 再按上述步骤重新测量。模态实验布点如图 5所示。
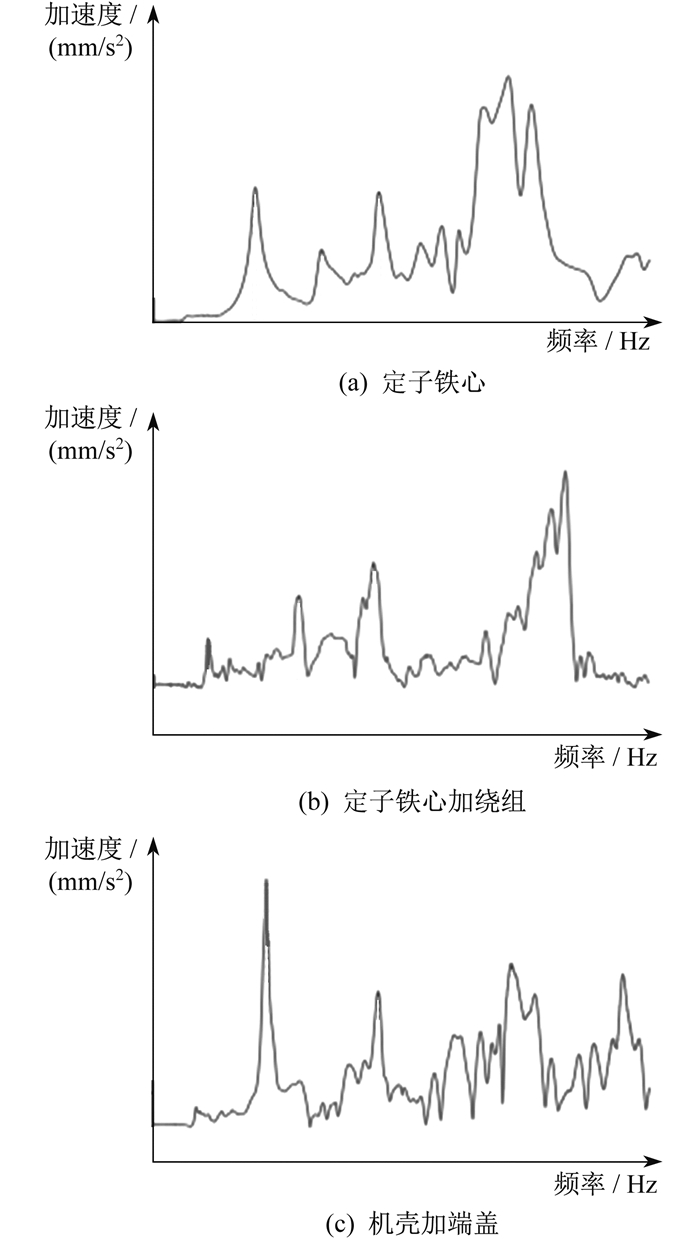
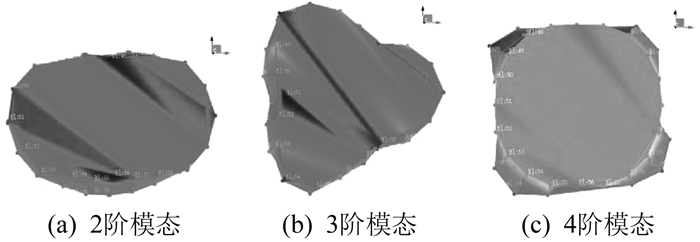
为了减少由于干扰信号造成的误差, 并提高力锤信号与加速度信号之间的相关性, 本文采取对同一点重复敲击并对传递函数取平均值的方法, 以保证分析结果的可靠性。各实验结构的模态识别频响函数如图 6所示。被测结构部分振型如图 7所示。
表 3为实验测得的3种结构的固有频率和阻尼比。
表 3
3种结构的固有频率和阻尼比
| 阶数 | 定子铁心 | 定子铁心加绕组 | 机壳加端盖 | |||||
| 频率 /Hz |
阻尼 比/% |
频率 /Hz |
阻尼 比/% |
频率 /Hz |
阻尼 比/% |
|||
| 2 | 794 | 2.86 | 1 296 | 1.62 | 3 408 | 2.73 | ||
| 3 | 2 274 | 0.37 | 3 487 | 1.15 | 6 683 | 1.62 | ||
| 4 | 4 051 | 2.05 | 5 879 | 0.93 | 8 668 | 0.80 | ||
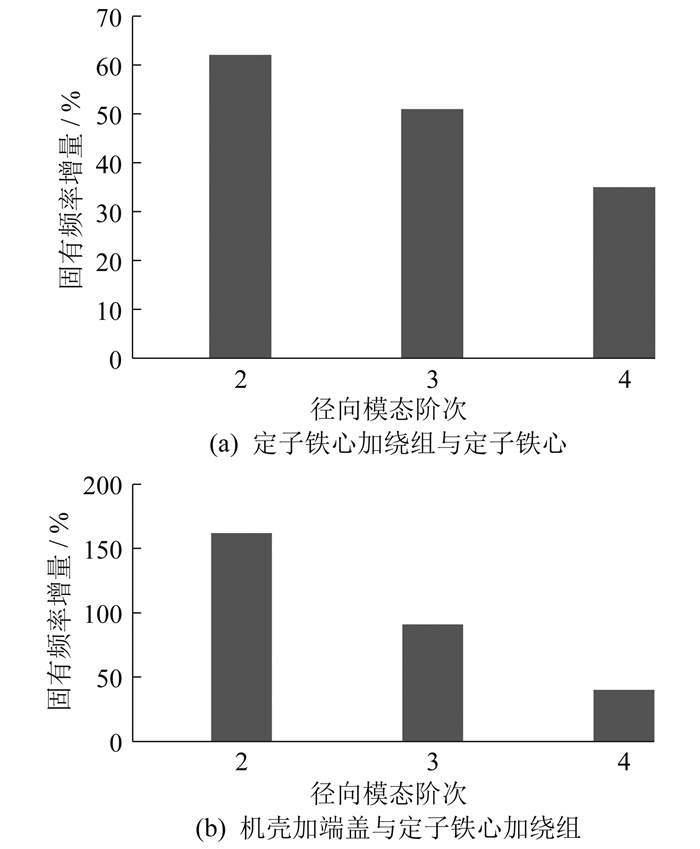
图 8为不同结构对径向模态频率的相对增量。
4 结果对比及分析
表 4为两种方法下不同定子结构的固有频率结果对比。
表 4
两种方法下不同定子结构固有频率结果对比
| 阶数 | 结构 | 频率/Hz | 误差/% | |
| 三维有限元法 | 锤击法 | |||
| 2 | 定子铁心 | 840 | 794 | 5.7 |
| 定子铁心加绕组 | 1 352 | 1 296 | 4.3 | |
| 机壳加端盖 | 3 579 | 3 408 | 5.0 | |
| 3 | 定子铁心 | 2 397 | 2 274 | 5.4 |
| 定子铁心加绕组 | 3 611 | 3 487 | 3.5 | |
| 机壳加端盖 | 6 958 | 6 683 | 4.1 | |
| 4 | 定子铁心 | 4 269 | 4 051 | 5.4 |
| 定子铁心加绕组 | 6 071 | 5 879 | 3.3 | |
| 机壳加端盖 | 9 027 | 8 668 | 4.1 | |
由表 4可知: 锤击法实验结果小于三维有限元法实验结果。原因可能在于: 一是有限元模型仿真时并未考虑阻尼, 电机阻尼比损耗对实验结果产生了影响; 二是进行锤击法模态实验时, 力锤造成的激励位置及幅值无法完全相同, 且依据频率响应函数选择固有频率时也容易产生误差, 但误差很小, 平均误差为4.53%, 最终结果在工程可接受范围内。
5 结论
PMSM的发展对电机提出了高固有频率的指标要求。在材料一定的情况下, 提高电机刚度能提升电机的固有频率。电机的加工工艺、浸漆质量、机壳和定子的配合、端盖和机座的配合等都是影响电机刚度的重要因素。本文通过对不同定子结构固有频率的仿真及实验验证, 得到以下结论。
(1) 在考虑材料的各向异性、绕组机壳和端盖影响的基础上, 建立了精确的电机结构有限元模态仿真模型, 获得了绕组、机壳和端盖对电机各阶固有频率的影响。实验发现, 不同电机定子固有频率与仿真的平均误差为4.53%。这一结果验证了仿真的准确性。
(2) 绕组、机壳和端盖对定子结构径向各阶模态频率的影响程度不同。对2阶、3阶和4阶模态频率来说, 随着模态频率的增加, 机壳对合成结构的刚度贡献逐渐减弱, 质量贡献逐渐增加。
(3) 机壳和端盖在一定程度上提高了结构轴向两端的刚度, 因此端盖的刚度和安装工艺, 对提升电机刚度和电机固有频率具有重要作用。
参考文献
-
[1]舒波夫. 电机的噪声和振动[M]. 沈官秋, 译. 北京: 机械工业出版社, 1980: 80-97.
-
[2]JACEK F G, CHONG W, JOSEPH C L. Noise of polyphase electric motors[M]. Boca Raton: CRC/Taylor & Francis, 2006: 43-65.
-
[3]ISHIBASHI F, KAMIMOTO K, HAYASHI T, et al. Natural frequency of stator core of small induction motor[J]. IET Electric Power Applications, 2003, 150(2): 210-214. DOI:10.1049/ip-epa:20020829
-
[4]HATTORI T, NARITA K, YAMADA T, et al. Modeling method of vibration analysis model for permanent magnet motor using finite element analysis[C]//International Conference on Electrical Machines and Systems. Tokyo, Japan: IEEE, 2009: 1-6.
-
[5]王天煜, 王凤翔, 白浩然, 等. 大型异步电机结构振动特性的研究[J]. 机械强度, 2009, 31(1): 140-143.
-
[6]代颖, 崔淑梅, 宋立伟. 车用电机的有限元模态分析[J]. 中国电机工程学报, 2011, 31(9): 100-105.
-
[7]李晓华, 黄苏融, 张琪. 电动汽车用永磁同步电机定子结构固有频率分析[J]. 中国电机工程学报, 2017, 37(8): 2383-2390.
-
[8]HONG J, WANG S, SUN Y, et al. A method of modal parameter estimation of the motor based on electromagnetic vibration exciter[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2636-2643. DOI:10.1109/TIA.2020.2981572
-
[9]肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.