|
|
|
发布时间: 2024-02-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-07-16
中图法分类号: TM711
文献标识码: A
文章编号: 2096-8299(2024)01-0073-07
|
摘要
节点脆弱性评估对配电网风险预警、安全运行具有关键作用。为此, 提出了一种计及设备健康指数的配电网节点脆弱性评估方法。首先, 从设备维度出发, 基于全生命周期理论得到节点设备本身和网络中的健康指数, 以此得到配电网节点脆弱性预评估方案; 然后, 针对配电网的辐射状特性, 在系统维度下基于复杂网络理论和风险理论, 提出了改进评估指标; 接着, 利用改进评估指标对设备维度下配电网节点脆弱性预评估方案进行再辨识, 得到配电网节点脆弱性排序; 最后, 以IEEE 33节点配电系统为例, 对算例结果进行分析, 并与其他文献结果进行对比, 验证了所提方法的合理性和可行性。
关键词
配电网; 节点脆弱性评估; 设备健康指数; 复杂网络理论; 风险评估
Abstract
Node vulnerability assessment plays a key role in risk warning and safe operation of distribution networks. To this end, a node vulnerability assessment method for distribution networks taking into account the equipment health index is proposed. Firstly, the health indices of the node equipment itself and the network are obtained from the equipment dimension based on the whole life cycle theory, so as to obtain the distribution network node vulnerability pre-assessment scheme. Next, in view of the radial characteristics of the distribution network, the improved assessment indexes are proposed in the system dimension based on the complex network theory and the risk theory. Then, the improved assessment indexes are utilized to carry out a re-identification of the node vulnerability pre-assessment scheme of the distribution grid in the equipment dimension, so as to obtain the node vulnerability assessment scheme of the distribution network. identification, and obtain the distribution network node vulnerability ranking. Finally, the IEEE 33 node distribution system is examplified, and the data analysis of the example results and the comparison of the results of other literature verify the reasonableness and feasibility of the method provided.
Key words
distribution networks; node vulnerability assessment; equipment health index; complex network theory; risk assessment
配电网处于电力系统末端, 直接面向终端用户, 是电力系统的重要组成部分[1]。配电网节点是能量汇聚和传输的关键位置。配电网节点脆弱性是指从网络中有选择地去除某节点所导致的网络性能下降的程度[2]。如果配电网节点被破坏, 将对配电网运行安全直接造成影响。因此, 开展配电网节点脆弱性评估非常重要。
目前, 在脆弱性评估方面已开展了大量研究, 但其主要着眼于输电网脆弱性评估。文献[3]改进了基于节点负荷平衡的故障动态模型, 并构造了基于线路电抗的加权输电网拓扑模型, 以此对输电网全局脆弱性进行评估, 但缺乏对输电网局部脆弱性评估的分析。文献[4]从局部和全局、有功和无功两方面综合评估输电网脆弱性, 构建了互补性脆弱度指标集和综合脆弱度模型, 但指标考虑的因素较为单一。针对该问题, 文献[5]在输电网特征模型中考虑了准稳态功率分布因子, 提出了从系统设备重要性来分析设备脆弱性的方法, 扩大了脆弱性指标的范围; 文献[6-7]从复杂网络理论和风险理论两方面提出了输电网静态综合指标, 实现了对输电网脆弱性评估; 文献[8]考虑了输电网实际运行时的基本电气规律和物理特性约束, 在功率传输路径、路径传输能力等方面改进已有输电网复杂模型, 以此对输电网脆弱性进行评估; 文献[9]提出了基于最大边介数生成树的输电网络拓扑改进方法, 并根据脆弱性评估指标设计了相应的攻击模式, 实现了对输电网脆弱性评估。
配电网脆弱性评估方面的研究成果目前相对较少。文献[10]基于抗毁性分析对中压配电网的拓扑结构进行改进, 建立了抗毁性优化模型, 以此对配电网安全可靠性进行分析。文献[11-12]从主观和客观两方面综合考虑了度值、介数等指标, 实现了对配电网节点脆弱度高低的排序, 但该文献所考虑的指标不符合配电网实际运行情况。针对该问题, 文献[13-14]提出了新的节点度数、节点介数和线路度数等概念, 并考虑了分布式电源的影响, 其综合脆弱性指标更符合配电网实际情况, 更适用于配电网脆弱性评估。由于配电网与输电网之间存在拓扑结构差异, 并且配电网多为开环运行的辐射状网络, 所以输电网脆弱性评估方面已有的研究成果难以直接移植到配电网脆弱性评估中。
目前, 配电网脆弱性评估方法还存在不足和需要改进之处, 主要包括以下两方面: 一是对配电网脆弱性评估角度单一, 未考虑节点设备本身健康指数的影响(节点设备健康指数是衡量设备本身及其在网络中健康水平的度量值, 健康指数越小, 设备本身及其在网络中的性能越差), 无法满足多维度评估的需要; 二是针对配电网辐射状的拓扑特性, 配电网脆弱性评估指标还未进行改善。
为此, 本文提出了一种计及设备健康指数的配电网节点脆弱性评估方法。首先, 在设备维度下基于全生命周期理论得到节点设备本身和网络中的健康指数, 以此为基础, 得到配电网节点脆弱性预评估方案; 然后, 针对配电网的辐射状特性, 在系统维度下基于复杂网络理论和风险理论提出了改进评估指标; 接着, 利用改进评估指标对配电网节点脆弱性预评估方案进行再辨识, 得到了配电网节点脆弱性排序; 最后, 以IEEE 33节点配电系统为例, 验证本文所提方法的合理性和可行性。
1 配电网设备维度下节点脆弱性评估
配电网节点脆弱性评估不仅需要从网络系统角度出发, 还需要从节点设备本身的角度来进行评估。因此, 基于节点设备本身的角度对节点脆弱性进行预评估是本文首先要解决的问题。本文基于全生命周期理论首先计算节点设备的故障率, 得到节点设备本身和网络中的健康指数, 继而得到配电网节点脆弱性预评估方案。
1.1 基于全生命周期理论的节点设备健康指数
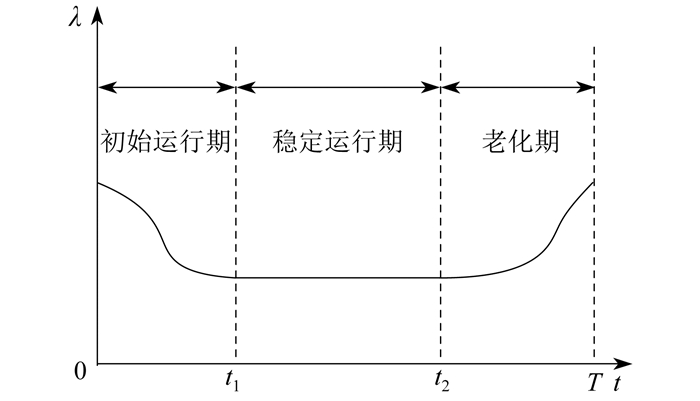
由于配电网节点设备健康指数与设备故障率密切相关, 故障率越低, 健康性能越好, 所以根据全生命周期理论, 将节点设备分为初始运行期、稳定运行期、老化期3个阶段[15]。节点设备故障率与其生命周期密切相关, 二者呈“浴盆”曲线。节点设备故障率浴盆曲线如图 1所示。
其中, t为设备使用时间, t1和t2分别为初始和稳定运行期时限, T为使用年限, λ为节点设备故障率。
在初始运行期, 节点设备故障率不断降低但高于稳定运行期的故障率; 在老化期, 节点设备使用年限过长, 导致其故障率不断增加。但配电网设备繁杂, 本文仅考虑配电网中的常规设备, 如配电变压器、开关设备、配电线路、断路器等。
利用配电网中常规设备在不同使用时间下运行与状态评价的历史数据, 可得到相应的设备故障率数据。设备故障率λ与使用时间存在相关联关系, 利用威尔分布可表示为
| $\lambda= \begin{cases}\alpha t^{(\beta-1)}, & t \in\left[0, t_1\right) \\ \alpha, & t \in\left[t_1, t_2\right](0 \leqslant \beta \leqslant 1) \\ \alpha t^{(1-\beta)}, & t \in\left(t_2, T\right]\end{cases}$ | (1) |
式中: α——设备稳定运行期的固定故障率。
因此, 根据节点设备故障率λ计算其健康指数H, 两者之间的关系为
| $H=C \mathrm{e}^{K_\lambda}$ | (2) |
式中: C——比例系数;
K——曲率系数。
1.2 基于成功流法的节点网络健康指数
成功流法是基于配电网系统结构图确保系统成功运行的分析方法。对于设备间关系明确、结构清晰的系统, 可以更优地反映出设备与网络间的功能和逻辑关系[16]。因此, 本文以设备健康指数为基础, 利用成功流法计算节点网络健康指数。本文假设配电网在实际运行时为开环状态, 故障时不考虑馈线之间负荷转移的影响, 且配电网中常规设备健康指数由前述方法计算得到。
基于成功流法计算配电网节点网络健康指数时, 首先对配电网节点设备的故障率λ数据进行预处理, 将其转化为概率形式。之后依据节点设备的健康状态筛选去除各种故障组合, 得到节点设备的健康指标H, 利用成功流法计算节点设备的健康正常概率pGO为
| $p_{\mathrm{GO}}=1-\frac{\lambda}{N}$ | (3) |
式中: N——某时间段, 本文取8 760 h。
由于节点设备故障率λ与健康指数H之间满足指数型关系, 则可得到故障概率p1为
| $p_1=\mathrm{e}^{-\left(\frac{H-10}{H}\right)^2}$ | (4) |
健康正常概率pGO与故障概率p1为互补关系, 表示为
| $p_{\mathrm{GO}}=g(H)=1-p_1$ | (5) |
根据配电网系统层次图自下而上以此等值, 本文对每条分支线路做串联处理, 某些重要用户采用双回线。采用并联分析, 利用等值健康正常概率代替同线路上全部设备的健康正常概率。
| $ p_{m n, s}=g\left(H_{m n, s}\right)$ | (6) |
| $p_{m n}=\prod\limits_{s \in S} p_{m n, s} $ | (7) |
| $p_{m n}^{\prime}=1-\left(1-P_{m n, 1}\right)\left(1-P_{m n, 2}\right)$ | (8) |
式中: pmn, s——第m层总负荷中第n条分支线路上设备s的健康正常概率;
Hmn, s——第m层总负荷中第n条分支线路上设备s的健康指数;
pmn——第m层总负荷中第n条分支线路等值成功运行概率;
S——设备集合;
p′mn——并联双回线路的健康正常概率;
pmn, 1, pmn, 2——并联双回线路中第1回线和第2回线的健康正常概率。
将每m层结果作为一个等值设备Nm放入下一层中。等值设备Nm的健康正常概率pNm为
| $p_{N m}=\sum\limits_{n=1}^l b_{m n} p_{m n} $ | (9) |
| $\sum\limits_{n=1}^l b_{m n}=1$ | (10) |
式中: l——分支线路总条数;
bmn——第m层总负荷中第n条分支线路所占比重。
当配电网网络等值至最顶层时, 得到最终健康正常概率pNm, 并以此得到节点设备网络健康指数Hall。
| $H_{\text {all }}=\frac{10}{1+\sqrt{-\ln \left(1-P_{N m}\right)}}$ | (11) |
因此, 从设备维度下将系统失负荷率作为评价指标, 系统失负荷率L可利用设备本身健康指数和网络中的健康指数得到。
| $L=\frac{P_{\text {loss }}}{\sum P_{\text {load }}}$ | (12) |
| $P_{\mathrm{loss}}=\frac{\sqrt{\sum\limits_{m=1}^M\left[\xi_1(t) H \xi_2(t) H_{\mathrm{all}}\right]^2}}{\sqrt{\sum\limits_{m=1}^M \xi_1^2(t) \xi_2^2(t)}}$ | (13) |
式中: Ploss——系统损失负荷;
Pload——系统总负荷;
M——总负荷层数;
ξ1(t)——节点设备健康指数权重;
ξ2(t)——节点设备网络健康指数权重。
2 配电网系统维度下节点脆弱性评估指标
2.1 基于复杂网络理论的节点脆弱性评估指标
节点度是指配电网节点间的连接程度, 节点度越大表明有更多节点与其相连, 其在网络中的地位更重要[19]。由于配电网具有辐射状的拓扑特性, 可能导致配电网在正常运行时节点度相同, 不具有差异性, 故以往的定义无法作为评估指标。本文针对配电网结构特性改进节点度指标, 不仅考虑局部影响, 而且从全局重要性进行考虑。配电网是由边和节点组成的整体, 节点之间相互影响, 因此建立了节点重要度矩阵DF。从全局角度出发引入了网络效率的概念, 更好地评估网络中某节点到另一节点的平均难易程度, 效率越大表明该节点所处位置越重要, 节点i的网络效率Ei为
| $E_i=\frac{1}{w} \sum\limits_{j=1, j \neq i}^w \frac{1}{d_{i j}}$ | (14) |
式中: w——拓扑节点数;
dij——节点i和j之间的最短距离。
节点的重要度矩阵DF需要综合考虑节点度和网络效率, 节点度和网络效率越大, 则重要度越大。
| $D_{\mathrm{F} i j}=\xi_{i j} T_j \frac{E_i}{k^2}$ | (15) |
式中: DFij——重要度矩阵DF中第i行第j列元素;
ξij——邻接矩阵中的第i行第j列元素, 这里邻接矩阵表示的是两个节点之间的连接关系, 若两节点之间相互连接, 其元素为1, 否则为0;
Tj——节点j的度;
k——节点平均度。
将节点i的网络效率和重要度结合计算, 得到节点i的改进节点度指标Ti1为
| $T_{i 1}=\left(T_j+\sum\limits_{j=1, j \neq i}^w D_{\mathrm{F} i j}\right) E_i$ | (16) |
随着高比例分布式能源的并网, 在配电网节点脆弱性评估中需要考虑分布式发电(Distributed Generation, DG)运行的影响, 计及DG出力影响, 得到节点i的改进介数指标Ti2为
| $T_{i 2}=\sum\limits_{i, e \in U_1, v \in U_2} \frac{\sqrt{S_{\mathrm{p} e} S_{\mathrm{lv}}}}{S_{\mathrm{b}}} O_{e v}(i)$ | (17) |
式中: e——电源节点;
v——负荷节点;
U1, U2——等值电源节点和等值负荷节点集合;
Spe——电源节点e输出视在功率;
Slv——负荷节点v消耗视在功率;
Sb——系统基准容量;
Oev(i)——节点e和v间最短路径比较函数。
在配电网开环运行的条件下, 节点连接损耗越大, 其对网络影响越大。因此, 引入电源节点功率权重, 节点i的改进连接损耗指标Ti3为
| $T_{i 3}=1-\sum\limits_{i, e \in U_1} \frac{S_{\mathrm{p}e}}{S_{\mathrm{all}}} \frac{E_e(i)}{M}$ | (18) |
式中: Sall——等值电源总视在功率;
Ee(i)——判断函数, 若电源节点e与节点i相通为1, 否则为0。
2.2 基于风险理论的节点脆弱性评估指标
配电网脆弱性评估不仅考虑其拓扑结构, 还需要考虑节点的运行特性。风险理论从配电网故障发生概率和故障造成后果两方面对节点脆弱性进行评估。这是目前配电网脆弱性评估常用的方法。节点电压越限是基于风险理论的配电网脆弱性评估指标之一, 因此本文利用节点电压越限评估配电网节点脆弱性。节点i电压越限指标Ui为
| $U_i=p_{\mathrm{r}i} J_{\mathrm{r} i}$ | (19) |
| $p_{\mathrm{r} i}= \begin{cases}1-\frac{1}{\mathrm{e}^{10 \Delta U_{\mathrm{N}}\left(u_i-1\right)}}, \quad u_i \in\left(1, 1+\Delta U_{\mathrm{N}}\right) \\ 1-\frac{1}{\mathrm{e}^{-10 \Delta U_{\mathrm{N}}\left(u_i-1\right)}}, \quad u_i \in\left(1-\Delta U_{\mathrm{N}}, 1\right] \\ 1, \quad u_i \in\left(0, 1-\Delta U_{\mathrm{N}}\right] \cup\left[1+\Delta U_{\mathrm{N}}, +\infty\right)\end{cases}$ | (20) |
| $J_{\mathrm{r} i}=\frac{\left(u_i-1\right)^2}{\Delta U_{\mathrm{N}}^2}$ | (21) |
式中: pri——节点i电压越限的概率;
Jri——节点i电压越限破坏程度;
ui——节点i的电压;
ΔUN——配电网允许电压偏差。
3 配电网节点脆弱性评估过程
通过复杂网络理论和风险理论得到的各指标数值相互之间存在量纲不同的问题。为此, 本文对所得评估指标进行归一化处理。
3.1 节点脆弱性评估指标的标准化处理
为解决评估指标之间量纲不同, 无法进行比较的问题, 本文利用Min -Max方法对各指标进行标准化处理, 将结果归一在[0, 1]。
| $z_i^*=\frac{z_i-z_{\min }}{z_{\max }-z_{\min }}$ | (22) |
式中: zi*——脆弱性评估指标归一化后的值;
zi——原始指标值;
zmin, zmax——指标内最小值、最大值。
配电网系统维度下节点脆弱性评估指标Ri是改进节点度指标、改进介数指标、改进连接损耗指标和节点电压越限指标的加权之和。其计算公式为
| $R_i=a_1 T_{i 1}+a_2 T_{i 2}+a_3 T_{i 3}+a_4 U_i$ | (23) |
式中: a1——改进节点度指标权重系数;
a2——改进介数指标权重系数;
a3——改进连接损耗指标权重系数;
a4——节点电压越限指标权重系数。
本文为综合分析各指标对节点脆弱性评估结果的影响, 采用了等权重的设置方法。
3.2 节点脆弱性评估流程
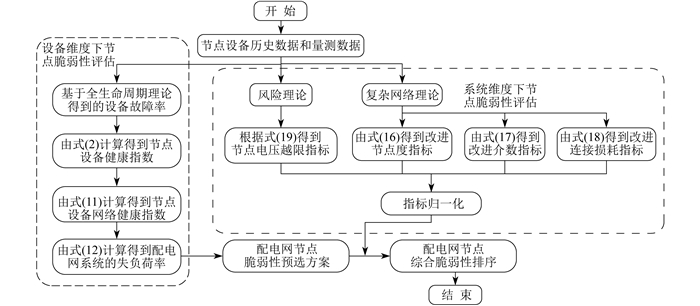
计及设备健康系数的配电网节点脆弱性评估流程如图 2所示。
4 算例验证
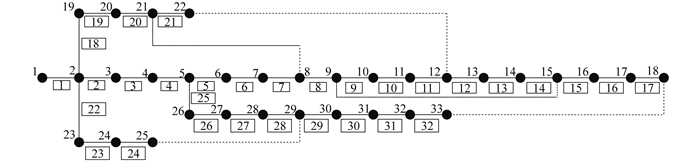
4.1 系统设置
4.2 配电网节点脆弱性预评估
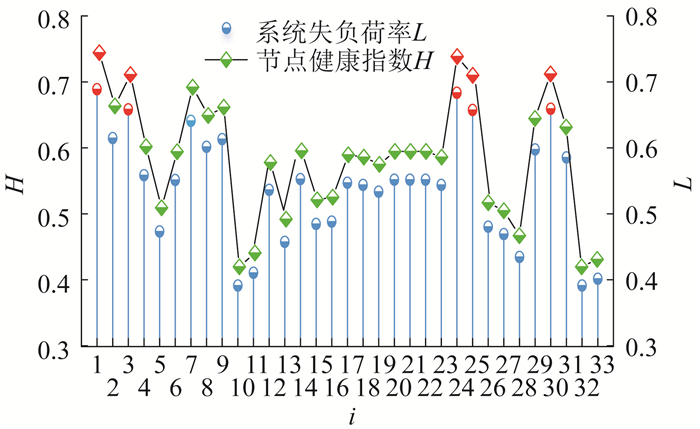
本文主要利用配电网常规设备的历史数据和在线监测数据来计算节点设备健康指数和网络健康指数, 以此得到节点脆弱性评估指标系统失负荷率。当网络中某节点设备故障时, 整个系统失负荷率越大, 造成的网络性能下降程度越大, 该节点脆弱性越高。配电网节点脆弱性预评估结果如图 4所示。
图 4表明, 配电网设备维度下节点脆弱性评估指标系统失负荷率L与节点设备健康指数H密切相关。配电网节点脆弱性预评估结果中, 节点1, 3, 24, 25, 31排名较高。从配电网实际运行状态分析, 该类节点多为电源节点或关键负荷节点, 其节点设备健康指数较高, 节点的脆弱性也较高。当该类节点故障时, 由于其处于网络拓扑结构关键位置, 会对配电网造成严重影响。本文首先得到设备维度下配电网节点脆弱性预评估方案, 为系统维度下评估节点脆弱性建立基础。
4.3 系统维度下节点脆弱性评估指标
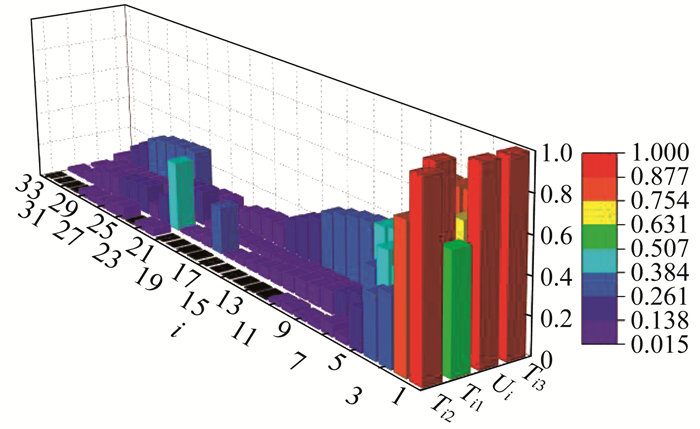
本文从系统维度下提出了改进节点度指标、改进介数指标、改进连接损耗指标和节点电压越限指标来对配电网节点脆弱性预评估方案进行再辨识, 归一化后节点各类型脆弱性评估指标结果如图 5所示, 具体数据如表 1所示。
表 1
归一化后节点各类型脆弱性评估指标数据
| i | Ti1 | Ti2 | Ti3 | Ui | i | Ti1 | Ti2 | Ti3 | Ui | |
| 1 | 0.623 4 | 1.000 0 | 1.000 0 | 1.000 0 | 18 | 0.263 6 | 0.006 2 | 0.127 8 | 0.036 2 | |
| 2 | 1.000 0 | 0.762 2 | 0.871 6 | 0.695 2 | 19 | 0.056 2 | 0.003 5 | 0.119 3 | 0.034 7 | |
| 3 | 0.632 6 | 0.373 6 | 0.760 8 | 0.315 6 | 20 | 0.040 6 | 0.001 6 | 0.100 6 | 0.033 5 | |
| 4 | 0.415 4 | 0.331 6 | 0.756 7 | 0.296 0 | 21 | 0.016 8 | 0.000 5 | 0.065 9 | 0.032 6 | |
| 5 | 0.480 0 | 0.217 5 | 0.755 6 | 0.259 4 | 22 | 0.396 0 | 0.045 6 | 0.110 2 | 0.196 2 | |
| 6 | 0.356 2 | 0.035 3 | 0.443 3 | 0.088 8 | 23 | 0.159 2 | 0.033 7 | 0.105 6 | 0.188 4 | |
| 7 | 0.177 9 | 0.065 4 | 0.425 6 | 0.085 2 | 24 | 0.075 8 | 0.008 8 | 0.068 6 | 0.180 9 | |
| 8 | 0.141 0 | 0.022 4 | 0.401 0 | 0.054 2 | 25 | 0.167 2 | 0.074 2 | 0.310 6 | 0.113 6 | |
| 9 | 0.118 0 | 0.018 4 | 0.390 6 | 0.052 1 | 26 | 0.154 0 | 0.065 8 | 0.304 8 | 0.109 2 | |
| 10 | 0.106 5 | 0.027 0 | 0.377 4 | 0.050 9 | 27 | 0.141 0 | 0.041 0 | 0.297 2 | 0.097 2 | |
| 11 | 0.097 2 | 0.022 5 | 0.364 6 | 0.050 1 | 28 | 0.123 2 | 0.035 0 | 0.287 2 | 0.091 0 | |
| 12 | 0.086 8 | 0.009 2 | 0.344 2 | 0.048 6 | 29 | 0.123 2 | 0.037 0 | 0.262 2 | 0.086 9 | |
| 13 | 0.076 2 | 0.006 2 | 0.319 7 | 0.047 2 | 30 | 0.092 0 | 0.007 3 | 0.207 4 | 0.083 6 | |
| 14 | 0.057 6 | 0.003 5 | 0.260 5 | 0.035 0 | 31 | 0.061 4 | 0.003 4 | 0.156 2 | 0.081 6 | |
| 15 | 0.043 5 | 0.001 6 | 0.223 9 | 0.034 6 | 32 | 0.016 1 | 0.000 2 | 0.059 3 | 0.021 6 | |
| 16 | 0.032 4 | 0.001 0 | 0.178 2 | 0.033 3 | 33 | 0.022 4 | 0.000 5 | 0.064 8 | 0.019 2 | |
| 17 | 0.015 0 | 0.000 5 | 0.119 7 | 0.032 6 |
由图 5和表 1可知, 各指标的最大值并不是同一节点, 不同节点在不同的指标下所得到的脆弱度不同, 需要在多指标下综合评估配电网节点脆弱度。改进节点度指标、改进节点介数指标和改进连接损耗指标侧重于反映节点在配电网结构中的重要程度, 而节点电压越限指标侧重于反映去除节点后所造成影响的严重程度。因此, 本文在系统维度下将各种指标进行综合分析, 结果如表 2所示。
表 2
系统维度下节点脆弱性评估指标
| i | Ri | i | Ri | i | Ri | i | Ri | |||
| 1 | 0.860 8 | 10 | 0.134 9 | 19 | 0.106 9 | 28 | 0.140 2 | |||
| 2 | 0.892 1 | 11 | 0.128 6 | 20 | 0.083 3 | 29 | 0.126 5 | |||
| 3 | 0.517 0 | 12 | 0.120 0 | 21 | 0.059 2 | 30 | 0.104 8 | |||
| 4 | 0.434 7 | 13 | 0.109 0 | 22 | 0.095 5 | 31 | 0.082 8 | |||
| 5 | 0.402 5 | 14 | 0.091 8 | 23 | 0.173 6 | 32 | 0.041 0 | |||
| 6 | 0.294 5 | 15 | 0.078 8 | 24 | 0.129 7 | 33 | 0.041 1 | |||
| 7 | 0.197 4 | 16 | 0.066 9 | 25 | 0.133 9 | |||||
| 8 | 0.160 9 | 17 | 0.047 6 | 26 | 0.174 4 | |||||
| 9 | 0.143 2 | 18 | 0.052 2 | 27 | 0.154 3 |
4.4 配电网节点脆弱性评估结果
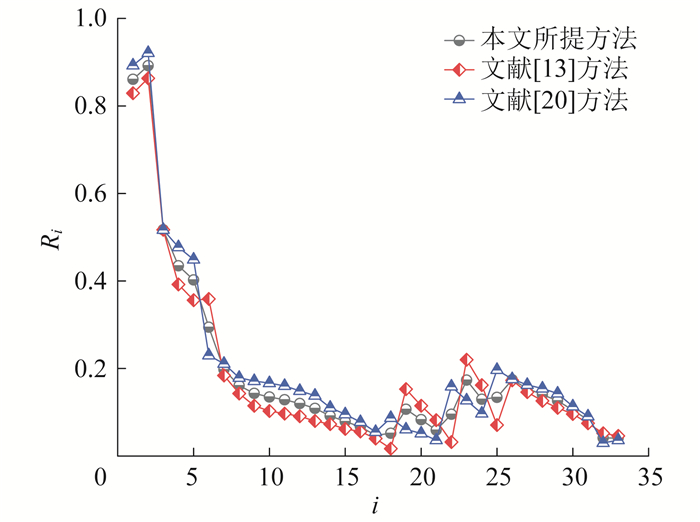
上文中利用系统维度下节点脆弱性评估指标对节点预评估方案进行评估, 得到如表 2所示的配电网节点评估结果。再将本文所提方法与文献[13]、文献[20]所提方法得到的配电网系统维度下节点脆弱性评估指标Ri进行对比, 验证其合理性和可行性, 结果如图 6所示。
文献[13]是将复杂网络理论与风险理论结合, 提出了配电网节点脆弱性评估指标。文献[20]是以配电网节点网络结构重要度和安全度为基础, 提出配电网节点脆弱性辨识模型。由图 6可知, 本文所提方法与其余两种方法评估结果趋势基本一致, 脆弱度高的节点均能区分出来, 说明本文所提方法的正确性。本文所提方法从设备和系统两个维度出发对配电网节点脆弱性进行评估, 并针对配电网辐射状特性改进了配电网节点脆弱性评估指标, 能更好地对有源配电网的节点脆弱性进行评估。
5 结语
本文根据配电网辐射状特性, 从配电网本身设备和系统两个角度出发, 实现了对配电网节点脆弱性评估。采用IEEE 33节点配电系统与其他文献所提方法作对比分析, 结果验证了本文所提方法的合理性和可行性。为进一步完善配电网整体脆弱性评估, 接下来应重点研究配电网线路脆弱性评估方法。
参考文献
-
[1]王梓旭, 林伟, 杨知方, 等. 考虑负荷弹性空间的配电网可靠性扩展规划方法[J]. 中国电机工程学报, 2022, 42(18): 6655-6668.
-
[2]丁明, 过羿, 张晶晶, 等. 基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估[J]. 电工技术学报, 2015, 30(3): 214-223. DOI:10.3969/j.issn.1000-6753.2015.03.027
-
[3]丁明, 韩平平. 加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报, 2008, 28(10): 20-25.
-
[4]倪向萍, 梅生伟, 张雪敏. 基于复杂网络理论的输电线路脆弱度评估方法[J]. 电力系统自动化, 2008, 32(4): 1-5.
-
[5]苏慧玲, 李扬. 从电力系统复杂网络特征探讨元件的脆弱性[J]. 电力系统自动化, 2012, 36(23): 12-17.
-
[6]肖盛, 张建华, 肖河. 基于复杂网络理论与风险理论的地区电网脆弱性评估[J]. 电网与清洁能源, 2013, 29(6): 21-28.
-
[7]王志强, 李欣, 李岩, 等. 基于复杂网络与风险的电网综合脆弱性评估[J]. 现代电力, 2014, 31(3): 49-55.
-
[8]徐敬友, 陈冲, 罗纯坚, 等. 基于改进复杂网络模型的电网关键环节辨识[J]. 电力系统自动化, 2016, 40(10): 53-61.
-
[9]陈志鹏, 谢宁, 王承民, 等. 基于分形机理的复杂电力网络脆弱性评估及鲁棒性提升策略研究[J]. 电网技术, 2021, 45(2): 657-665.
-
[10]杨丽徙, 曾新梅, 方强华, 等. 基于抗毁性分析的中压配电网络拓扑结构[J]. 电力系统自动化, 2013, 37(8): 65-69.
-
[11]吴辉, 彭敏放, 张海艳, 等. 基于复杂网络理论的配电网节点脆弱度评估[J]. 复杂系统与复杂性科学, 2017, 14(1): 38-45.
-
[12]ZHANG Y, SONG X, XIE L, et al. Vulnerable point identification using heterogeneous interdependent node theory for distribution systems[J]. CSEE Journal of Power and Energy Systems, 2022, 8(2): 591-598.
-
[13]史文超, 李晓明, 王孝琳, 等. 配电网脆弱性评估方法[J]. 电力系统及其自动化学报, 2018, 30(12): 125-131.
-
[14]CHOWDHURY T, CHAKRABARTI A, CHANDA C K. Analysis of vulnerability indices of power grid integrated DG units based on complex network theory[C]//2015 Annual IEEE India Conference (INDICON). New Delhi, India: IEEE, 2015: 1-5.
-
[15]苏东, 马仲能, 李成翔, 等. 配网开关柜全生命周期成本模型及敏感度分析[J]. 电力系统保护与控制, 2018, 46(1): 150-155.
-
[16]李辉, 张孝军, 潘华, 等. 面向智能变电站通信网络可靠性研究[J]. 电力系统保护与控制, 2021, 49(9): 165-171.
-
[17]刘文通, 舒勤, 钟俊, 等. 基于局部电压稳定指标及复杂网络理论的无功电压分区方法[J]. 电网技术, 2018, 42(1): 269-278.
-
[18]张娟, 童晓阳, 姜建伟. 基于渗流和风险理论的电力系统连锁故障分析[J]. 电力系统自动化, 2017, 41(5): 46-52.
-
[19]王子欣, 苗世洪, 郭舒毓, 等. 考虑分布式电源出力随机特性的配电网节点脆弱性评估[J]. 电力自动化设备, 2021, 41(8): 33-40.
-
[20]孙顺祥, 李晓明, 张繁碧, 等. 基于网络结构重要度和安全隐患脆弱度的配电网脆弱线路辨识[J]. 电力系统保护与控制, 2018, 46(14): 107-113.