|
|
|
发布时间: 2024-02-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-11-30
基金项目: 国家自然科学基金(52006131);国家电网公司华东分部科技项目(H2021-111)
中图法分类号: TK01+8
文献标识码: A
文章编号: 2096-8299(2024)01-0066-07
|
摘要
为了提高综合能源系统运行的经济性和环保性, 提出了一种计及综合需求响应的综合能源系统优化调度模型, 分别以系统运行成本最低和碳排放成本最低为目标, 利用改进的黏菌算法进行优化求解。以某工业园区为研究对象, 进行算例验证。结果表明, 该系统考虑综合需求响应对负荷侧用能起到良好的"削峰填谷"的效果, 改进黏菌算法可明显降低系统的运行成本和碳排放成本, 验证了模型和改进算法的有效性和可行性。
关键词
综合能源系统; 综合需求响应; 优化调度; 黏菌算法
Abstract
In order to improve the economic and environmental performance of integrated energy systems, an integrated energy system optimization model that takes into account integrated demand response is proposed, using an improved slime mold algorithm for optimization and solution, with the goal of minimizing system operating costs and carbon emission costs, respectively. Using a certain industrial park as an object for verification, the results show that integrated demand response can have a good "peak shaving and valley filling" effect on load side energy consumption. Improved slime mold algorithm can significantly reduce the operating and carbon emission costs of the system, verifying the effectiveness and feasibility of the model and improved algorithm.
Key words
integrated energy system; integrated demand response; optimize scheduling; slime mold algorithm
随着全球经济快速发展, 能源短缺与环境污染问题愈发严重。综合能源系统(Integrated Energy System, IES)能够多梯级利用能源, 可以促进可再生能源消纳, 是实现节能减排的有效途径, 可推动实现我国提出的“双碳”目标[1-4]。
目前, 关于IES模型已有大量的相关研究。文献[5]建立了结合可再生能源以及储能装置的IES模型, 文献[6]建立了工业园区低碳经济运行的IES模型。但上述研究只建立了供能侧的模型, 未考虑到用能侧的优化。针对这一问题, 文献[7]考虑了针对电力系统的电负荷需求响应; 文献[8]引入价格弹性矩阵描述需求响应行为, 并分析了其有效性; 文献[9]引入可转移负荷对负荷侧用能进行优化。但上述研究未考虑不同负荷响应特性的情况。
IES优化调度模型具有大规模、非线性、非凸的特点。文献[10-11]采用粒子群优化(Particle Swarm Optimization, PSO)算法以及改进PSO算法优化IES模型, 但PSO算法搜索速度较慢, 精度不高, 易陷入局部最优。文献[12-13]提出用灰狼优化(Grey Wolf Optimizer, GWO)算法求解IES优化调度问题, 算法性能明显提升, 但搜索速度仍有待提高。文献[14]采用麻雀搜索算法(Sparrow Search Algorithm, SSA)对IES优化调度问题进行求解, 搜索速度快, 但初始最优解较差, 算法性能仍有待提升。
综上所述, 本文建立计及综合需求响应(Integrated Demand Response, IDR)的IES优化调度模型, 提出了一种改进的黏菌优化算法(Slime Mould Algorithm, SMA), 求解IES优化调度问题, 并结合算例进行仿真验证, 为IES的实际调度运行问题的求解提供参考。
1 系统建模
1.1 IES模型
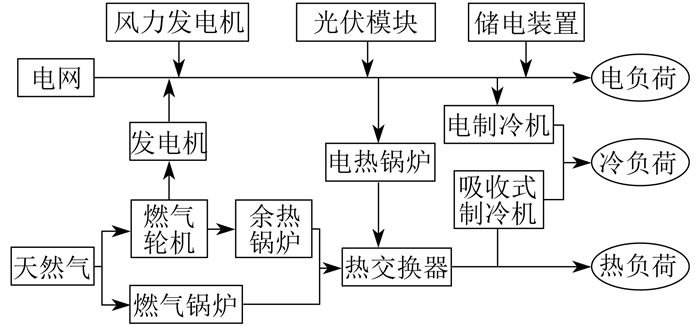
IES架构如图 1所示。
从能量平衡角度, 建立图 1中各设备数学模型如下。
燃气轮机(Gas Turbine, GT)模型为
| $ \left\{\begin{array}{l} P_{\mathrm{GT} . \mathrm{e}}=\eta_{\mathrm{GT}}^{\mathrm{e}} P_{\mathrm{GT} . \mathrm{g}} \\ P_{\mathrm{GT} . \mathrm{h}}=\eta_{\mathrm{GT}}^{\mathrm{h}} P_{\mathrm{GT} . \mathrm{g}} \end{array}\right. $ | (1) |
式中: PGT.e, PGT.g, PGT.h——GT发电功率、耗气功率、产热功率;
ηGTe, ηGTh——GT发电效率、产热效率。
余热锅炉(Waste Heat Boiler, WHB)模型为
| $ P_{\mathrm{WHB}}=\frac{\left(1-\eta_{\mathrm{GT}}^{\mathrm{h}}\right)}{\eta_{\mathrm{GT}}^{\mathrm{h}}} P_{\mathrm{GT} . \mathrm{h}} \eta_{\mathrm{WHB}} $ | (2) |
式中: PWHB——WHB输出功率;
ηWHB——WHB产热效率。
燃气锅炉(Gas Boiler, GB)模型为
| $ P_{\mathrm{GB} . \mathrm{h}}=\eta_{\mathrm{GB}}^{\mathrm{h}} P_{\mathrm{GB} . \mathrm{g}} $ | (3) |
式中: PGB.h, PGB.g——GB产热功率、耗气功率;
ηGBh——GB产热效率。
电热锅炉(Electric Boiler, EB)模型为
| $ P_{\text {EB. h }}=\eta_{\mathrm{EB}}^{\mathrm{h}} P_{\mathrm{EB}} $ | (4) |
式中: PEB.h, PEB——EB产热功率、消耗电功率;
ηEBh——EB产热效率。
电制冷机(Electric Chiller, EC)模型为
| $ P_{\mathrm{EC} . \mathrm{c}}=K_{\mathrm{COP}}^{\mathrm{EC}} P_{\mathrm{EC}} $ | (5) |
式中: PEC.c, PEC——EC输出制冷功率、输入电功率;
KCOPEC——EC制冷系数。
吸收式制冷机(Absorption Chiller, AC)模型为
| $ P_{\text {AC. c }}=K_{\mathrm{COP}}^{\mathrm{AC}} P_{\mathrm{AC}} $ | (6) |
式中: PAC.c, PAC——AC制冷功率、输入热功率;
KCOPAC——AC制冷系数。
风力发电机(Wind Turbine, WT)模型为
| $ P_{\mathrm{WT}}= \begin{cases}0, & v<v_{\text {in }} \\ P_{\mathrm{WT}}^{\mathrm{o}} \frac{v^K-v_{\mathrm{in}}^K}{v_{\mathrm{r}}^K-v_{\mathrm{in}}^K}, &\ \ v_{\mathrm{in}} \leqslant v<v_{\mathrm{r}} \\ P_{\mathrm{WT}}^{\mathrm{o}}, & v_{\mathrm{r}} \leqslant v<v_{\text {out }} \\ 0, & v \geqslant v_{\text {out }}\end{cases} $ | (7) |
式中: PWT, PWTo——WT输出功率、额定输出功率;
v, vin, vr, vout——实际风速、启动风速、额定风速、切出风速;
K——出力特性系数。
光伏(Photovoltaic, PV)模块模型为
| $ P_{\mathrm{PV}}=f_{\mathrm{PV}} P_{\mathrm{n}, \mathrm{PV}} \frac{I^t}{I_{\mathrm{s}}}\left[1+\varepsilon_{\mathrm{p}}\left(t_{\mathrm{PV}}^t-t_{\mathrm{n}}\right)\right] $ | (8) |
式中: PPV, Pn, PV——光伏模块输出功率、额定输出功率;
fPV——能源转换效率;
It, Is——t时刻辐射强度、标准辐射强度;
εp——温度功率系数;
tPVt, tn——t时刻光伏模块温度、额定温度。
储电装置(Electric Storage, ES)模型为
| $ E_{\mathrm{ES}}^t=\left(1-\mu_{\mathrm{e}}\right) E_{\mathrm{ES}}^{t-1}+\eta_{\text {in }}^{\mathrm{e}} P_{\text {in }}^{\mathrm{e}}(t)-\frac{P_{\text {out }}^{\mathrm{e}}(t)}{\eta_{\text {out }}^{\mathrm{e}}} $ | (9) |
式中: EESt——t时刻ES充放电能量;
μe——ES自放电率;
ηine, ηoute——ES充放电效率;
Pine(t), Poute(t)——t时刻ES充放电功率。
1.2 需求响应模型
在负荷侧通过引导用户主动改变原有用能需求及习惯, 从而改善源荷两侧供需的不平衡关系, 提高系统运行经济性。根据负荷响应特性, 需求响应可分为价格型需求响应和替代型需求响应[15]。
价格型需求响应模型为
| $ L_{\mathrm{m}}^t=L_{\mathrm{m}, 0}^t\left(1+E_{\mathrm{m}} \frac{c_{\mathrm{m}}^t-c_{\mathrm{m}, 0}^t}{c_{\mathrm{m}, 0}^t}\right) $ | (10) |
式中: Lm, 0t, Ltm——t时刻响应前后负荷量;
Em——弹性系数;
cm, 0t, cmt——t时刻响应前后能源价格。
替代型需求响应模型为
| $ \left\{\begin{array}{l} \Delta L_t^{\mathrm{r}, \mathrm{e}}=-\varepsilon_{\mathrm{e}, \mathrm{h}} \Delta L_t^{\mathrm{r}, \mathrm{ch}} \\ \varepsilon_{\mathrm{e}, \mathrm{h}}=\frac{v_{\mathrm{e}} \varphi_{\mathrm{e}}}{v_{\mathrm{h}} \varphi_{\mathrm{h}}} \end{array}\right. $ | (11) |
式中: ΔLtr, e,ΔLtr, ch——t时刻可替代电负荷量、被替代冷或热负荷量;
εe, h——电热替代系数;
ve, vh——电能和热能的单位热值;
φe, φh——电能和热能的能源利用率。
2 目标函数与约束条件
2.1 目标函数
目标函数分为以IES在运行过程中运行成本最小为目标和碳排放成本最小为目标两种。
2.1.1 运行成本
IES运行成本Ch包括购电成本Ce、购气成本Cg以及系统运维成本Cop。
| $ C_{\mathrm{h}}=C_{\mathrm{e}}+C_{\mathrm{g}}+C_{\mathrm{op}} $ | (12) |
购电成本Ce为
| $ C_{\mathrm{e}}=\sum\limits_{t=1}^T\left(c_{\mathrm{b}, t} P_{\mathrm{b}, t}-c_{\mathrm{s}, t} P_{\mathrm{s}, t}\right) $ | (13) |
式中: T——运行周期时长;
cb, t, cs, t——t时刻购、售电电价;
Pb, t, Ps, t——t时刻向上级电网购、售电功率。
购气成本Cg为
| $ C_{\mathrm{g}}=\sum\limits_{t=1}^T c_{\mathrm{g}} P_{\mathrm{g}, t} $ | (14) |
式中: cg——购买天然气单价;
Pg, t——t时刻购买天然气功率。
系统运维成本Cop为
| $ C_{\mathrm{op}}=\sum\limits_{t=1}^T \sum\limits_{i=1}^9 \omega_i P_{i, t} $ | (15) |
式中: i——IES设备, i=1, 2, 3, …9分别表示GT, WHB, GB, EB, EC, AC, WT, PV, ES;
ωi——设备i的运维系数;
Pi, t——t时刻设备i的输出功率。
2.1.2 碳排放成本
| $ C_{\mathrm{H}}=W \sum\limits_{t=1}^T\left[\mu_{\mathrm{e}} P_{\mathrm{b}, t}+\mu_{\mathrm{f}} P_{\mathrm{g}, t}\right] $ | (16) |
式中: CH——碳排放成本;
W——惩罚系数, 包括排放惩罚和环境价值;
μe——单位电功率对应的CO2排放系数;
μf——单位体积天然气对应的CO2排放系数。
2.2 约束条件
设备功率约束条件为
| $ \left\{\begin{array}{l} P_{\mathrm{GT}}^{\min } \leqslant P_{\mathrm{GT} \cdot \mathrm{g}} \leqslant P_{\mathrm{GT}}^{\max } \\ P_{\mathrm{GB}}^{\min } \leqslant P_{\mathrm{GB} \cdot \mathrm{h}} \leqslant P_{\mathrm{GB}}^{\max } \\ P_{\mathrm{EB}}^{\min } \leqslant P_{\mathrm{EB} \cdot \mathrm{h}} \leqslant P_{\mathrm{EB}}^{\max } \\ P_{\mathrm{EC}}^{\min } \leqslant P_{\mathrm{EC} \cdot \mathrm{c}} \leqslant P_{\mathrm{EC}}^{\max } \\ P_{\mathrm{AC}}^{\min } \leqslant P_{\mathrm{AC} \cdot \mathrm{c}} \leqslant P_{\mathrm{AC}}^{\max } \\ E_{\mathrm{ES}}^{\min } \leqslant E_{\mathrm{ES}}^t \leqslant E_{\mathrm{ES}}^{\max } \end{array}\right. $ | (17) |
式中: Pjmax, Pjmin——设备j输出功率上下限, 其中j为GT, GB, EB, EC, AC;
EESmax, EESmin——ES储电容量上下限。
电、热、冷能功率平衡约束条件为
| $ \left\{\begin{array}{l} P_{\mathrm{GT.e}}-P_{\mathrm{EB}}-P_{\mathrm{EC}}+P_{\mathrm{WT}}+P_{\mathrm{PV}}- \\ \ \ \ \ P_{\mathrm{in}}^{\mathrm{e}}+P_{\mathrm{out}}^{\mathrm{e}}+P_{\mathrm{b}, t}-P_{\mathrm{s}, t}=L_{\mathrm{e}} \\ P_{\mathrm{WHB}}+P_{\mathrm{GB} . \mathrm{h}}+P_{\mathrm{EB} . \mathrm{h}}=L_{\mathrm{h}} \\ P_{\mathrm{EC}.\mathrm{c}}+P_{\mathrm{AC} . \mathrm{c}}=L_{\mathrm{c}} \end{array}\right. $ | (18) |
式中: Le, Lh, Lc——系统的电、热、冷负荷量。
3 算法介绍
3.1 SMA
SMA通过模拟黏菌捕食实现智能寻优功能。黏菌在觅食过程中的位置变化如下:
| $ \boldsymbol{X}(k+1)=\left\{\begin{array}{l} r_1 \cdot\left(\boldsymbol{U}_{\mathbf{B}}-\boldsymbol{L}_{\mathbf{B}}\right)+\boldsymbol{L}_{\mathbf{B}}, \quad r_1<z \\ \boldsymbol{X}_{\mathrm{b}}(k)+v_{\mathrm{b}} \cdot\left[\boldsymbol{W} \cdot \boldsymbol{X}_{\mathbf{A}}(k)-\boldsymbol{X}_{\mathbf{B}}(k)\right], \\ \ \ \ \ \ \ \ z \leqslant r_1<p \\ v_{\mathrm{c}} \cdot \boldsymbol{X}(k), \quad r_1 \geqslant p \end{array}\right. $ | (19) |
式中: X(k+1)——迭代第k+1次时更新后的黏菌位置;
r1——随机数;
UB, LB——搜索边界上下限;
z——常数, 取0.03;
Xb(k)——迭代第k次时黏菌最优个体位置;
vb, vc——随机数, vb∈[-a, a], vc∈[0, 1];
W——黏菌重量;
XA (k), XB (k)——迭代第k次时随机选择的黏菌个体位置;
X(k)——迭代第k次时黏菌位置。
p和a的公式如下:
| $ \left\{\begin{array}{l} p=\tanh \left|S-D_{\mathrm{F}}\right| \\ a=\operatorname{arctanh}\left[-\left(k / k_{\max }\right)+1\right] \end{array}\right. $ | (20) |
式中: S——当前黏菌个体的适应度;
DF——迭代过程中最佳适应度;
kmax——最大迭代次数。
3.2 改进SMA
SMA初始化种群时, 为了增强种群多样性, 将混沌映射与反向学习相结合, 得到基于混沌对立的学习策略。本文采用Sine映射, 数学模型为
| $ \boldsymbol{X}^{\mathrm{To}}=\boldsymbol{L}_{\mathrm{B}}+\boldsymbol{U}_{\mathrm{B}}+\lambda \cdot \boldsymbol{X}(k) $ | (21) |
式中: XTo, λ——种群中当前黏菌个体对应的混沌反向解和混沌映射值。
参数a的变化对迭代过程中开发和探索的平衡有重要影响。由式(20)可知, a在早期迭代中迅速下降, 在后期迭代中下降速度减慢, 不利于全局探索。为了提高全局探索能力和局部开发的收敛能力[16], 可将a定义为
| $ a=2.5\left(k / k_{\max }\right)^{2 k / k_{\max }} $ | (22) |
算术优化算法根据算术操作符的分布特性来实现全局寻优, 与SMA结合后, 可以有效改善SMA后期易陷入局部最优的缺点, 增强算法后期寻优随机性。改进SMA(以下简称“ISMA”)在更新黏菌位置时, 若r1<p, 则通过式(19)进行更新, 否则根据式(23)进行位置更新。
| $ \boldsymbol{X}(k+1)=\left\{\begin{array}{l} \frac{\boldsymbol{X}_{\mathrm{b}}(k)}{\left(p_{\mathrm{MO}}+\varepsilon\right)} \times \\ \quad\left[\left(\boldsymbol{U}_{\mathbf{B}}-\boldsymbol{L}_{\mathbf{B}}\right) \mu+\boldsymbol{L}_{\mathbf{B}}\right], r_2<0.5 \\ \boldsymbol{X}_{\mathrm{b}}(k) p_{\mathrm{MO}} \times \\ \quad\left[\left(\boldsymbol{U}_{\mathbf{B}}-\boldsymbol{L}_{\mathbf{B}}\right) \mu+\boldsymbol{L}_{\mathbf{B}}\right], r_2 \geqslant 0.5 \end{array}\right. $ | (23) |
式中: pMO——数学优化器概率;
ε——极小值;
μ——控制参数;
r2——随机数, 且r2∈[0, 1]。
4 算例分析
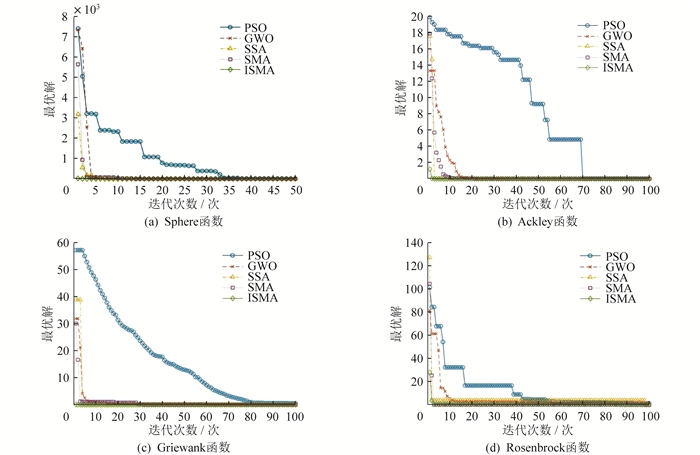
4.1 测试函数仿真
4.2 基础数据整理
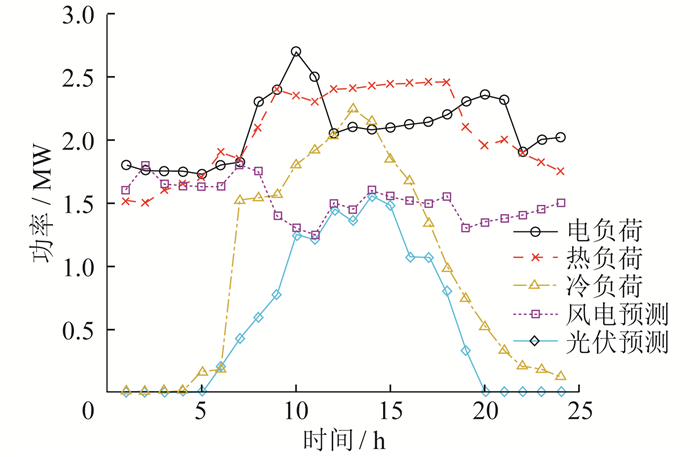
本文以某工业园区为研究对象, 每24 h为一个运行周期, 单位运行时间为1 h。系统中各设备关键参数如表 2所示, 分时购电电价如表 3所示。售电价格为0.5元/kWh, 天然气价格为2.55元/m3。系统典型日初始负荷、风电和光伏输出功率预测曲线如图 3所示。
表 2
系统中各设备关键参数
| 设备参数 | 数值 |
| GT输出功率上限/kW | 4 000 |
| GT发电效率/% | 30 |
| GT产热效率/% | 40 |
| WHB产热效率/% | 80 |
| GB输出功率上限/kW | 1 000 |
| GB产热效率/% | 90 |
| EB输出功率上限/kW | 400 |
| EB产热效率/% | 90 |
| EC制冷系数 | 3.5 |
| AC制冷系数 | 1.5 |
| ES储电容量上限/(kW/h) | 400 |
| ES初始容量/(kW/h) | 80 |
| ES充电效率/% | 95 |
| ES放电效率/% | 90 |
| ES最大充放电功率/kW | 250 |
表 3
分时购电电价
| 时段类型 | 时段 | 电价/(元/kWh) |
| 峰 | 09:00—12:00 | 1.09 |
| 19:00—22:00 | ||
| 平 | 08:00—09:00 | 0.68 |
| 12:00—19:00 | ||
| 22:00—24:00 | ||
| 谷 | 00:00—08:00 | 0.35 |
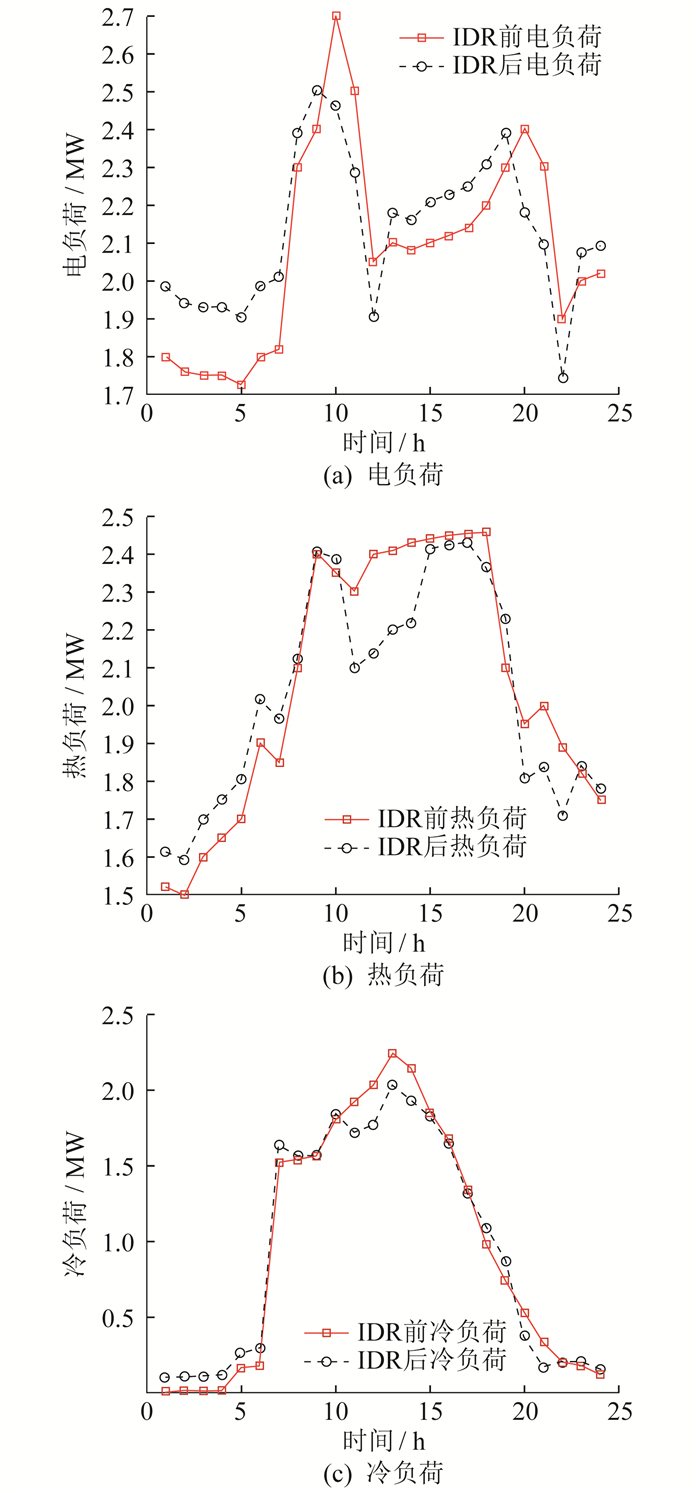
4.3 IDR结果分析
4.4 调度结果分析
为了验证ISMA的有效性, 针对系统的目标函数, 分别采用PSO算法、GWO算法、SSA、SMA和ISMA进行计算。不同算法的优化调度结果对比如表 4所示。
表 4
不同算法的优化调度结果对比
| 算法 | 以运行成本最小为目标 | 以碳排放成本最小为目标 | |||
| 总成本/元 | 碳排放量/kg | 总成本/元 | 碳排放量/kg | ||
| PSO | 25 863 | 28 581 | 28 716 | 26 641 | |
| GWO | 24 688 | 26 987 | 27 528 | 26 034 | |
| SSA | 24 551 | 26 560 | 27 346 | 25 998 | |
| SMA | 24 520 | 26 397 | 27 039 | 25 986 | |
| ISMA | 21 968 | 24 876 | 25 141 | 23 024 | |
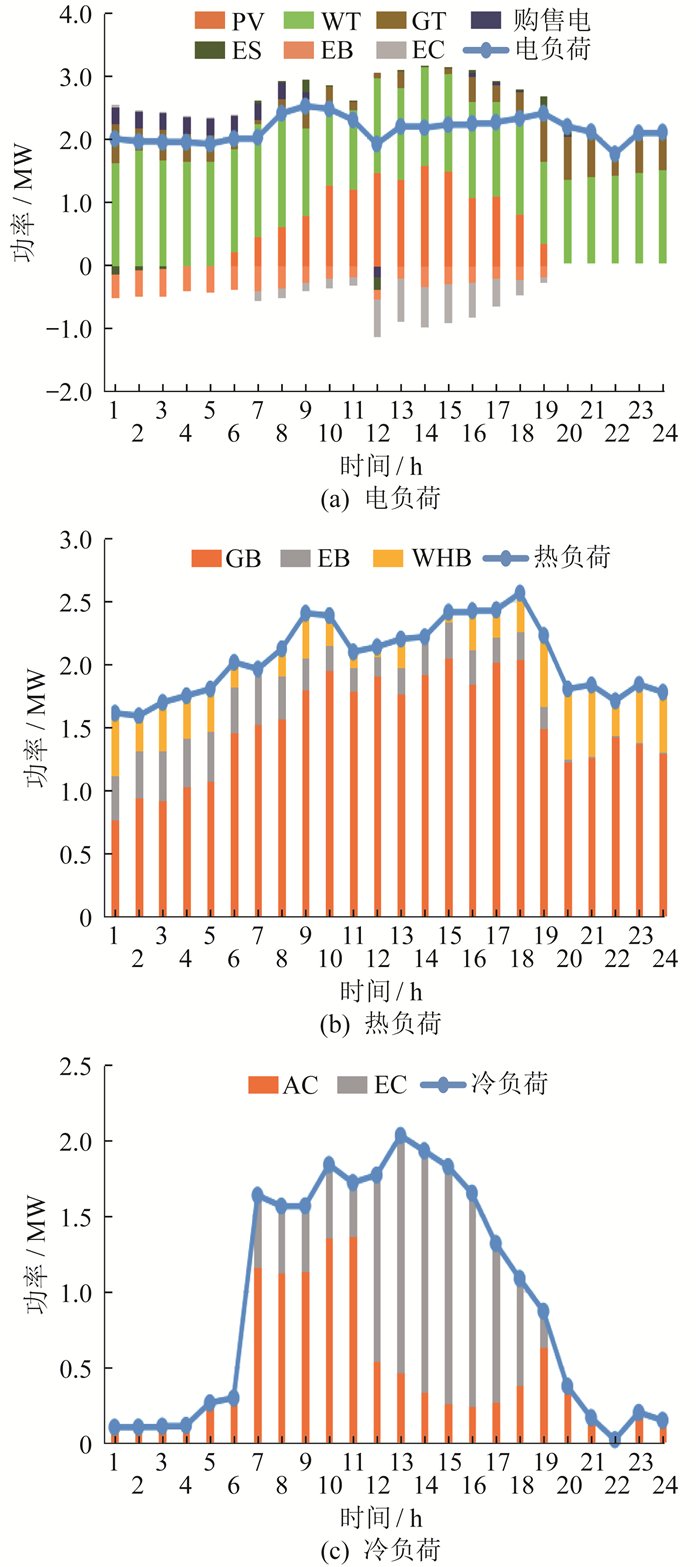
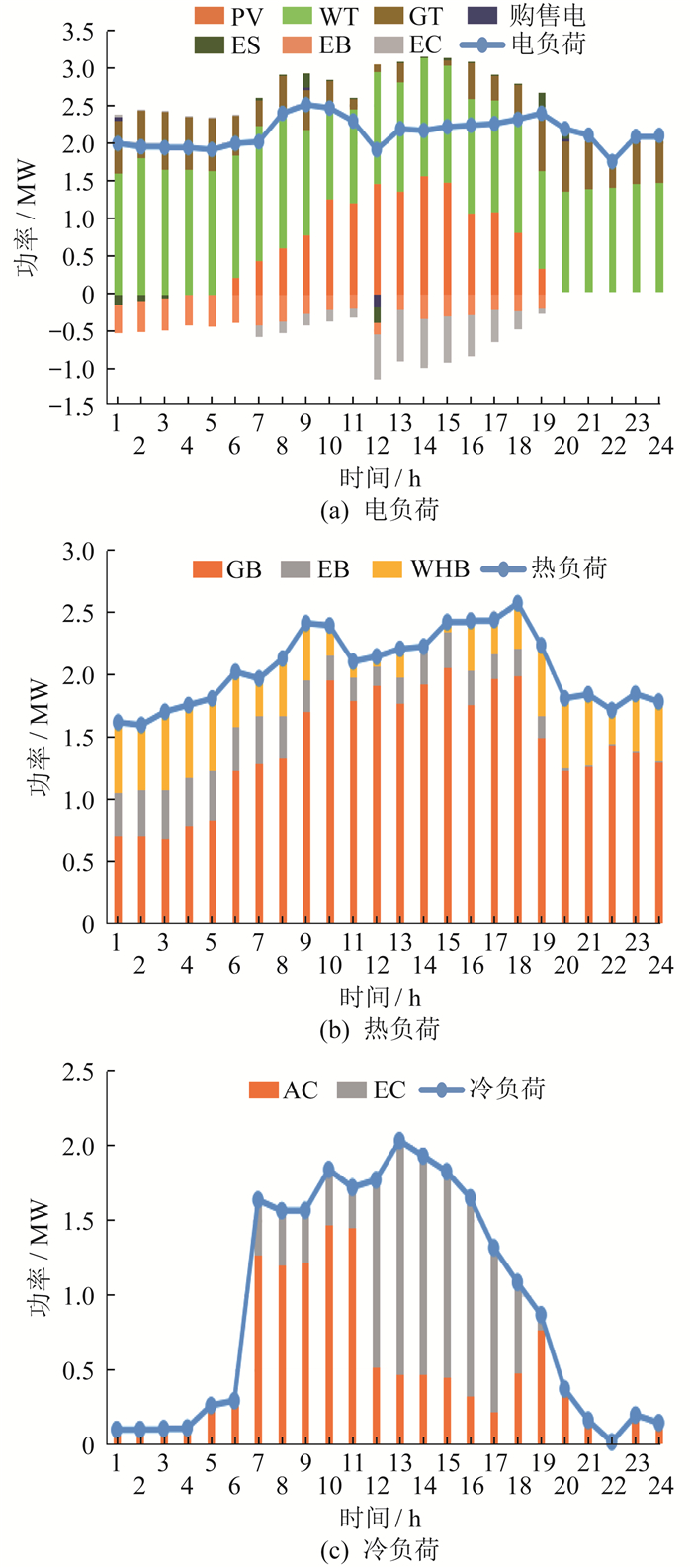
分析表 4中不同算法得到的最优值发现, ISMA可以找到更好的最优解, 总成本和碳排放量均低于其他算法。分别以运行成本最小和以碳排放成本最小为目标, 用ISMA得到的IES典型日目标函数的电、热、冷负荷平衡分布, 其分布情况如图 5和图 6所示。
分析图 5和图 6的ISMA优化调度结果, 可以得出以下结论。电负荷优先由可再生能源WT和PV提供, 当电能不足时, 由GT发电或从电网购买电能。当考虑系统运行成本最小为目标时, 在0:00—8:00分时电价为谷价期间, 增加向电网的购电量, 以减小系统运行成本; 当考虑系统碳排放成本最小为目标时, 由于GT的碳排放量比电网小, 因此考虑增加GT发电功率。在12:00—17:00 WT和PV发电高峰期间, 系统除满足电负荷需求外, 多余的电能可以通过EC以及EB释放冷热能, 做到多能互补, 增加风光消纳, 还可以售卖给电网。另外, ES可以在满足用户电负荷后, 存储多余的电能, 当电负荷不足时, 放电以补足电能。
对于热负荷, 优先使用WHB产生的热能, 不足部分由GB以及EB补充。
冷负荷在电能充足时段, 利用多余电能带动EC制冷, 其余时段则由AC制冷。
5 结论
本文研究了计及IDR的IES的优化调度问题, 分别构建了以系统运行成本最小和系统碳排放成本最小的目标函数, 对SMA进行改进得到ISMA, 通过算例仿真结果得出以下结论。
(1) 考虑IDR时, 电、热、冷负荷峰谷差分别降低了22.1%, 19.3%, 17.9%, 提高了系统经济性。
(2) 选用标准测试函数对比分析ISMA与PSO算法、GWO算法、SSA、SMA的优化曲线, ISMA算法在优化速度和精度上具有明显优势。
(3) 对比分析ISMA与PSO算法、GWO算法、SSA、SMA分别用于IES调度时的系统运行成本和碳排放成本, 并分析ISMA参与调度的电、热、冷负荷平衡分布情况, 发现ISMA在保证系统稳定运行的同时, 能够有效降低运行成本与碳排放成本。这可以为IES的实际运行调度提供参考。
参考文献
-
[1]郭祚刚, 袁智勇, 徐敏, 等. 多能互补综合能源系统混合能流计算方法及算例[J]. 综合智慧能源, 2022, 44(7): 58-65.
-
[2]李滔滔, 周登极, 马世喜, 等. 面向多时间断面的电-热综合能源系统分布式协同状态估计方法[J]. 动力工程学报, 2023, 43(5): 655-662.
-
[3]张爱平, 赵利兴, 刘静. 楼宇型综合能源服务系统智能优化运行研究[J]. 综合智慧能源, 2022, 44(2): 42-48.
-
[4]陈彦奇, 刘康祥, 赵鑫, 等. 基于阶梯型碳交易机制的综合能源系统低碳经济调度[J]. 动力工程学报, 2023, 43(7): 901-909.
-
[5]刘圣春, 宋丽莹, 代宝民, 等. 附加碳税的综合能源系统优化调度分析[J]. 工程热物理学报, 2022, 43(7): 1790-1800.
-
[6]李嘉祺, 陈艳波, 陈来军, 等. 工业园区综合能源系统低碳经济优化运行模型[J]. 高电压技术, 2022, 48(8): 3190-3200.
-
[7]HOSSEINNIA H, TOUSI B. Optimal operation of DG-based micro grid (MG) by considering demand response program (DRP)[J]. Electric Power Systems Research, 2019, 167: 252-260. DOI:10.1016/j.epsr.2018.10.026
-
[8]高佳, 肖迎群, 马蕊, 等. 考虑不确定性价格型需求响应的多源微网运行优化[J]. 现代电力, 2020, 37(4): 425-432.
-
[9]崔杨, 修志坚, 刘闯, 等. 计及需求响应与火储深度调峰定价策略的电力系统双层优化调度[J]. 中国电机工程学报, 2021, 41(13): 4403-4414.
-
[10]姚健, 刘爱军. 基于粒子群算法的区域综合能源优化调度方法[J]. 电力需求侧管理, 2022, 24(4): 67-72.
-
[11]陶静, 徐武, 李逸琳, 等. 基于多目标算法的冷热电联供型综合能源系统运行优化[J]. 科学技术与工程, 2019, 19(33): 200-205.
-
[12]尚佳炜, 李萍, 汤航, 等. 基于灰狼算法冷热电联供综合能源优化调度[J]. 工业控制计算机, 2022, 35(3): 40-43.
-
[13]续一臣, 王海云. 基于改进灰狼算法的微电网优化调度[J]. 计算机仿真, 2023, 40(3): 96-102.
-
[14]丁娅鑫, 熊军华. 基于改进麻雀算法的区域综合能源系统优化研究[J]. 自动化与仪表, 2022, 37(10): 24-29.
-
[15]魏震波, 马新如, 郭毅, 等. 碳交易机制下考虑需求响应的综合能源系统优化运行[J]. 电力建设, 2022, 43(1): 1-9.
-
[16]TANG A D, TANG S Q, HAN T, et al. A modified slime mould algorithm for global optimization[J]. Computational Intelligence and Neuroscience, 2021(11): 215-237.