|
|
|
发布时间: 2024-02-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-08-23
基金项目: 国家自然科学基金(52177098)
中图法分类号: TM77
文献标识码: A
文章编号: 2096-8299(2024)01-0058-08
|
摘要
随着可再生分布式电源(DG)在配电网中的渗透率不断提升, 如何充分利用DG与主网联合对非故障失电区域恢复供电引起了人们的重视。对孤岛与主网联合恢复供电的配合性以及风光荷的波动性问题进行了研究。首先, 综合考虑了风光荷的波动性问题, 建立了广度与深度优先搜索相结合的动态孤岛划分策略; 然后, 为实现孤岛与主网联合恢复供电的最优性, 建立了具有配合性的两阶段规划模型, 一阶段以主网通过重构恢复重要负荷最大化为目标, 二阶段以主网和DG孤岛联合恢复重要负荷最大化为目标, 两者目标之间存在一定的关联性, 能够实现联合恢复供电的整体寻优; 最后, 利用改进IEEE 33节点系统算例验证了所提方法的可行性与有效性。
关键词
配电网; 分布式电源; 孤岛划分; 供电恢复; 两阶段规划模型
Abstract
With the increasing penetration of renewable distributed generation in distribution networks, how to fully utilize the joint restoration of non-faulted blackout areas by DG and the main network has attracted much attention. This paper focuses on the coordination between islanded microgrids and the main network for joint power restoration, as well as the fluctuation issues of wind and solar loads. Firstly, a dynamic islanding partitioning strategy combining breadth-first search and depth-first search is proposed, considering the fluctuation issues of wind and solar loads. Secondly, in order to realize the optimality of the joint restoration of power supply between the island and the main network, a two-stage programming model with coordination is established. The first stage aims at maximizing the important load of the main network through reconstruction, and the second stage aims at maximizing the important load of the main network and the DG island. Due to the certain correlation between the two objectives, the overall optimization of the joint restoration of power supply can be realized. Finally, the feasibility and effectiveness of the proposed method are verified using an improved IEEE 33-node example.
Key words
distribution network; distributed generation; island partition; power restoration; two-stage programming model
故障后的配电网供电恢复技术是智能配电网的核心, 是提高配电网供电可靠性的重要保证[1]。近年来, 随着可再生能源的大力发展, 大量以风能、光能为代表的清洁能源并入配电网是必然趋势。然而, 由于风能、光能的波动性和不确定性, 以及配电网的复杂性, 所以配电网的供电恢复面临着诸多挑战。因此, 如何充分利用清洁分布式电源输出功率和主网的供电能力, 实现最大程度的失电负荷供电, 成为了智能配电网研究的重要方向。
目前, 许多学者已经针对含可再生能源的配电网供电恢复策略进行了研究。文献[2-3]通过对故障时段内失电负荷的综合评估, 优先保证对恢复评估系数较高的失电负荷恢复供电。文献[4]针对配电网内分布式电源(Distributed Generation, DG)实际输出功率和负荷需求值与预测值之间存在误差的问题, 利用模型预测控制理论进行多时步预测, 提高预测值的准确性, 并建立鲁棒优化模型实现配电网的供电恢复。该方法具有较强的抗参数扰动能力, 但为了减少计算量, 控制时步的选择是关键。文献[5]综合考虑了DG输出功率间隙性和负荷需求波动性问题, 建立了基于风光荷功率曲线的孤岛风险评估模型和多时段孤岛划分的方法。文献[6]对光伏发电功率进行离散概率建模, 较为充分地考虑了光伏发电的波动性问题, 提高了供电恢复方案的可行性。文献[7]考虑到负荷的时变性和可控性, 利用光储联合系统保证负荷的可靠恢复, 通过变异粒子群算法提高求解配电网故障恢复的速度。上述文献仅考虑孤岛, 未考虑到主网对失电负荷恢复供电作用。文献[8]综合考虑主网恢复能力和DG供电能力, 利用二者相结合的方式恢复供电, 针对失电负荷区域优先考虑进行孤岛划分恢复供电, 再对剩余区域建立恢复重构模型。文献[9]建立了配电网孤岛划分和网络重构的统一故障恢复模型。文献[10]建立孤岛和网络重构的双层规划模型, 在一定程度上解决了孤岛与重构的配合性问题, 但由于仅考虑常规DG接入的场景且未能考虑负荷需求的不确性问题, 故不符合实际配电网运行情况。
以上研究存在以下两个问题: 一是将风光输出功率和负荷需求值等效为恒定值, 会导致孤岛内功率不平衡, 进而出现电压、频率越限的问题; 二是将配电网供电恢复问题分为孤岛划分和网络重构两个子问题, 未考虑到两者对供电恢复的关联, 不能保证实现供电恢复方案的最优性。
本文提出的配电网供电恢复策略综合考虑了风光荷的时变性, 提出了主网与DG联合的供电恢复方案。通过该方案, 可以利用DG的发电能力和主网的供电能力, 最大程度地满足失电负荷需求。另外, 该策略的优化目标包括重要负荷恢复量最大化和网络损耗最小化, 以此实现对故障恢复方案的综合考虑。
1 源荷模型和可控电源评价系数
1.1 风机输出功率模型
风机的输出功率受多种因素的影响, 其中主要取决于当前时刻风速的大小[11]。风机的输出功率与风速的关系式为
| $P_{\mathrm{wl}, t}= \begin{cases}0, & v_t \leqslant v_{\mathrm{ci}} \text { 或 } v_t \geqslant v_{\mathrm{fi}} \\ \frac{P_{\mathrm{r}} v_t^3}{v_{\mathrm{rate}}^3-v_{\mathrm{ci}}^3}-\frac{P_{\mathrm{r}} v_{\mathrm{ci}}^3}{v_{\mathrm{rate}}^3-v_{\mathrm{ci}}^3}, & \ \ v_{\mathrm{ci}}<v_t<v_{\mathrm{rate}} \\ P_{\mathrm{r}}, & \ \ v_{\mathrm{rate}} \leqslant v_t<v_{\mathrm{fi}}\end{cases}$ | (1) |
式中: Pwt, t——t时刻风机的输出功率;
vt——t时刻的风速;
vci, vfi——风机的切入风速和切出风速;
Pr——风机的额定功率;
vrate——风机的额定风速。
1.2 光伏输出功率模型
光伏的输出功率主要受当前时刻的光照强度和光伏组件面积的影响[12]。光伏机组的输出功率与光照强度、光伏组件面积的关系式为
| $P_{\mathrm{pv}, t}= \begin{cases}A P_{\mathrm{std}} \frac{S_t^2}{S_{\mathrm{std}} k_{\mathrm{c}}}, & 0 \leqslant S_t<k_{\mathrm{c}} \\ A P_{\mathrm{std}} \frac{S_t}{S_{\mathrm{std}}}, &\ \ k_{\mathrm{c}} \leqslant S_t<S_{\mathrm{std}} \\ A P_{\mathrm{std}}, &\ \ S_t \geqslant S_{\mathrm{std}}\end{cases}$ | (2) |
式中: Ppv, t——t时刻光伏的输出功率;
A——光伏组件的面积;
Pstd——光伏机组的额定输出功率;
St, Sstd——实时光照强度、额定光照强度;
kc——特定光照强度, 当实时光照强度St超过kc后, 光伏机组的输出功率与光照强度的关系由非线性变为线性关系。
1.3 常规DG输出功率模型
微型燃气轮机、柴油机等常规的DG具有独立的调频、调压能力, 在故障恢复期间可作为黑启动电源。这类常规的DG运行需满足以下功率约束与爬坡约束[13]条件。
| $P_{\mathrm{DG}, i}^{\min } \leqslant P_{\mathrm{DG}, i} \leqslant P_{\mathrm{DG}, i}^{\max }$ | (3) |
| $Q_{\mathrm{DG}, i}^{\min } \leqslant Q_{\mathrm{DG}, i} \leqslant Q_{\mathrm{DG}, i}^{\max }$ | (4) |
| $-R_{\mathrm{DG}, i}^{P \mathrm{d}} \leqslant P_{\mathrm{DG}, i}(t)-P_{\mathrm{DG}, i}(t-1) \leqslant R_{\mathrm{DG}, i}^{P \mathrm{u}}$ | (5) |
| $-R_{\mathrm{DG}, i}^{Q \mathrm{~d}} \leqslant Q_{\mathrm{DG}, i}(t)-Q_{\mathrm{DG}, i}(t-1) \leqslant R_{\mathrm{DG}, i}^{Q \mathrm{u}}$ | (6) |
式中: PDG, imax, PDG, imin, QDG, imax, QDG, imin——负荷节点i上常规DG的有功、无功功率上下限;
PDG, i, QDG, i——负荷节点i上常规DG的有功、无功功率;
RDG, iPu, RDG, iPd, RDG, iQu, RDG, iQd——负荷节点i上常规DG有功、无功功率控制的光伏上、下爬坡率;
PDG, i(t), QDG, i(t)——负荷节点i上常规DG在t时刻的有功、无功功率。
1.4 负荷特性模型
本文从负荷需求的时变性和重要性两个角度进行分析。
(1) 负荷时变性模型由于负荷在不同时间段内所需求的功率值不同, 所以为保证方案的可行性, 需考虑负荷时变性。根据负荷节点类型, 将负荷节点分为政府和医疗负荷、商业负荷、居民负荷。对不同类型的日负荷曲线进行积分[14], 得到不同类型负荷随时间变化的功率需求值。
| $L_i(t)=\int_t^{t+1} f_i(x) \mathrm{d} x, \quad t=0, 1, 2, \cdots, 23$ | (7) |
式中: Li(t)——负荷节点i在t时刻的功率需求值;
fi(x)——负荷节点i的日负荷需求曲线。
(2) 负荷重要性由于不同负荷的中断对人身安全、经济损失所造成的影响程度不同, 因此将负荷分为3个级别, 即一级、二级和三级负荷[15]。其中, 一级负荷失去供电将对人身安全和经济造成极大的影响, 因此必须保证这类负荷在配电网发生故障时能够及时恢复供电, 以保证供电的可靠性。此外, 若存在可控负荷, 可通过调节可控负荷功率, 保证对重要负荷的优先供电。
1.5 可控电源评价系数
对于DG孤岛运行模式, 本文采用较为成熟的主从控制模式。针对一个孤岛内存在多个可控电源的主电源选取问题, 本文通过对可控电源评价, 选取可控电源系数最大的作为孤岛的主电源。定义第k个可控DG的评价系数为
| $K_k=P_{\mathrm{con}, k}^{\max }\left(P_{\mathrm{con}, k}^{\max }-P_{\mathrm{con}, k}^{\min }\right)$ | (8) |
式中: Kk——第k个可控DG的评价系数;
Pcon, kmax, Pcon, kmin——第k个可控DG输出功率的最大值、最小值。
2 孤岛划分策略
2.1 目标函数及约束条件
在配电网故障时段内采用风能、光能的实际输出功率和可控DG的最大输出功率作为孤岛的供电量。为保证重要负荷供电的优先性以及尽可能多地恢复失电负荷[16-17], 设置目标函数为
| $\max F_{\mathrm{DG}}=\sum\limits_{t=1}^T \sum\limits_{i \in D} \lambda_i P_{i, t}^0 y_{i, t}-\mu f_{\mathrm{loss}}$ | (9) |
式中: FDG——孤岛划分的目标函数;
T——故障持续时间;
D——所有失电负荷节点集合;
λi——负荷节点i的权重值;
Pi, t0——t时刻负荷节点i的功率需求值;
yi, t——负荷节点i在t时刻的通电状态, 取0或1, 若为1则表示恢复供电, 为0则表示未恢复供电;
μ——网损的权重值;
floss——孤岛内部的网络损耗。
需要满足的约束条件如下。
孤岛内功率平衡约束条件为
| $\sum\limits_{k=1}^m P_{k, t} \geqslant \sum\limits_{i \in I} L_{i, t}$ | (10) |
式中: m——孤岛内DG个数;
Pk, t——t时刻第k个DG的实际输出功率;
I——孤岛内负荷节点集合;
Li, t——孤岛内负荷节点i在t时刻的功率需求值。
负荷节点电压约束条件为
| $U_{\min } \leqslant U_{i, t} \leqslant U_{\max }$ | (11) |
式中: Umin, Umax——负荷节点i电压幅值的最小值、最大值;
Ui, t——t时刻负荷节点i的电压幅值。
网络潮流约束条件为
| $P_{i, t}-U_{i, t} \sum\limits_{j=1}^n U_{j, t}\left(G_{i j} \cos \delta_{i j, t}+B_{i j} \sin \delta_{i j, t}\right)=0$ | (12) |
| $Q_{i, t}-U_{i, t} \sum\limits_{j=1}^n U_{j, t}\left(G_{i j} \cos \delta_{i j, t}+B_{i j} \sin \delta_{i j, t}\right)=0$ | (13) |
式中: Pi, t, Qi, t——t时刻注入负荷节点i的有功、无功功率;
n——孤岛内负荷节点总个数;
Uj, t——t时刻节负荷节点j的电压幅值;
Gij, Bij, δij, t——t时刻节负荷节点i、j之间的电导、电纳和相角差。
支路功率约束条件为
| $P_{i j, t} \leqslant P_{i j, \max }$ | (14) |
式中: Pij, t——t时刻流过负荷节点i、j之间支路的有功功率;
Pij, max——负荷节点i、j之间支路允许流过的最大有功功率。
网络结构约束条件为
| $g \in G$ | (15) |
式中: g——配电网重构后的拓扑结构;
G——网络拓扑结构集合。
2.2 孤岛最优切负荷操作
在进行孤岛恢复时, 需要处理孤岛内风光荷波动给孤岛电量和功率平衡所带来的问题。若在故障恢复时间内, 存在孤岛内DG输出功率值小于负荷总需求值时, 可通过削减负荷来保证孤岛稳定运行。为保证孤岛切负荷的最优性, 从两个方面进行考虑: 一是优先削减孤岛内的可控负荷; 二是切除孤岛内的不可控负荷。具体操作步骤如下。
步骤1 将孤岛A内的可控负荷按照容量由小到大的原则进行排序, 并存入孤岛A的可控负荷节点集合DA, load, 通过对DA, load各元素求和得到可控负荷总容量LDA, load。
步骤2 在不满足孤岛A功率平衡约束时段, 计算孤岛内DG输出功率之和与负荷总需求的差值dif。
步骤3 对dif和LDA, load进行比较: 若dif≤LDA, load, 则可通过对可控负荷节点容量从小到大进行累计, 直到累计容量大于dif, 然后削减该部分可控负荷, 转至步骤7;若dif>LDA, load, 则转至步骤4。
步骤4 将孤岛A内所有可控负荷削减后, 再对孤岛A的最末端负荷节点进行标记, 得到待切负荷节点集合Cload。根据待切负荷节点的权重等级与功率需求值的积, 由小到大进行排序, 得到待切负荷顺序Mload。
步骤5 根据待切负荷顺序Mload, 对孤岛A进行切负荷操作, 更新待切负荷节点集合Cload。
步骤6 判断此时更新后的孤岛范围是否满足功率平衡约束。若满足, 则转至步骤7, 否则转至步骤4。
步骤7 将被切除负荷的节点标记为失电节点, 得到最终孤岛A的范围。
2.3 孤岛划分流程
由于风光荷的不确定性, 所以要根据不同故障时段的DG输出功率和负荷需求值进行动态孤岛划分, 采用广度和深度优先搜索相结合的方式确定孤岛供电范围。具体操作步骤如下。
步骤1 输入故障发生时刻、故障持续时间、故障位置, 以及确定故障时段内风能和光能输出功率、失电负荷的功率需求值和各个可控电源评价系数等。
步骤2 以可控电源所在节点为根节点, 以故障时刻DG输出功率值为半径进行搜索, 采用广度优先遍历确定该DG的功率圆。若功率圆包含其他不可控DG, 则更新功率圆半径, 继续搜索确定孤岛范围。
步骤3 判断孤岛之间是否存在负荷交叉的情况。若存在, 则进行孤岛合并, 针对孤岛合并后主电源的选取问题, 根据可控电源评价系数, 选取可控电源评价系数较大的DG作为孤岛合并后的主电源; 若不存在, 则转至步骤4。
步骤4 判断是否存在未划入孤岛区域内的一级失电负荷。若存在, 则以该一级负荷为根节点进行深度优先搜索, 找到最近的孤岛区, 然后并入到孤岛区域中; 否则转至步骤5。
步骤5 判断孤岛是否满足约束条件。若不满足, 则进行最优切负荷操作, 直至满足约束条件。
步骤6 判断故障时段数是否大于等于最大故障时段数: 若大于等于, 则生成最终孤岛划分策略; 否则转至步骤5。
3 两阶段规划的配电网供电恢复模型及求解流程
3.1 两阶段规划模型
在通过配电网主网和孤岛对失电负荷区域供电恢复时, 两者恢复供电的方式是彼此影响的, 已有算法将两者分成两个问题进行处理, 但未能充分体现出两者之间的配合性。为增加两者之间供电恢复的配合性, 本文采用两阶段规划模型, 通过设置目标函数之间的嵌套, 使两阶段的结果具有关联性, 以协同优化主网的故障恢复和孤岛划分, 从而实现全局最优的解决方案。
3.1.1 一阶段规划模型
一阶段规划模型考虑配电网主网的供电恢复力, 设定一阶段目标函数。
主网恢复系统失电负荷总量最大化:
| $\max f_1=\sum\limits_{t=1}^T \sum\limits_{i \in D} \lambda_i P_{i, t}^0 y_{i, t}$ | (16) |
式中: f1——主网恢复系统失电负荷总量。
系统网络损耗最小化:
| $\min f_2=\sum\limits_{t=1}^T \sum\limits_{l=1}^N k_l R_l \frac{P_i^2+Q_i^2}{U_i^2}$ | (17) |
式中: f2——系统网络损耗;
N——系统支路总数;
kl——支路l的开断状态, kl=1表示支路闭合, kl=0表示支路断开;
Rl——支路l的电阻;
Pi, Qi, Ui——支路l末端负荷节点i的有功功率、无功功率和电压值。
综合考虑以上两种因素, 设置一阶段目标函数为
| $\max F_1=f_1-\mu f_2$ | (18) |
式中: F1——一阶段目标结果。
上层规划需满足的约束条件为式(11)~式(15)以及开关动作次数约束式(19)。
| $\sum\limits_{t=1}^T \sum\limits_{q=1}^r\left|S_{t, q}-S_{t-1, q}\right| \leqslant R$ | (19) |
式中: r——开关总个数;
St, q——t时刻开关q的闭合状态, St, q=1表示开关闭合, St, q=0表示开关断开;
R——最大开关动作次数。
3.1.2 二阶段规划模型
在二阶段规划中, 以一阶段主网恢复结果为基础, 针对一阶段未恢复的失电负荷区域, 通过分布式电源在故障时期内形成孤岛, 以重要负荷恢复量最大化为目标, 为失电负荷恢复供电。目标函数为式(20), 约束条件为式(10)~式(15)。
| $\max F_2=F_1+F_{\mathrm{DG}}$ | (20) |
式中: F2——二阶段目标结果。
3.2 两阶段规划求解流程
两阶段规划求解具体操作步骤如下。
步骤1 输入基础数据, 包括网络结构、DG和负荷数据, 以及故障位置、故障发生时刻和持续时间等。
步骤2 采用灰狼优化算法[18]求解一阶段规划, 保留M种主网重构的供电恢复方案以及对应的甩负荷区域。
步骤3 在步骤2形成的主网重构方案基础上, 针对甩负荷区域, 采用广度与深度搜索算法相结合的方式进行孤岛划分。
步骤4 判断各个孤岛与主网重构层相连的开关是否断开: 若是, 则保留孤岛划分结果; 否则, 将该孤岛并入主网重构。
步骤5 判断是否满足约束条件: 若满足则将该孤岛并入主网; 若不满足则保留该孤岛区域。
步骤6 计算M种方案的二阶段目标函数值, 并保留最优的供电恢复方案。
步骤7 判断t是否大于等于最大故障持续时间: 若是, 则输出最优供电恢复方案; 否则, 令t+1并转至步骤2。
4 实验结果及分析
4.1 算例参数
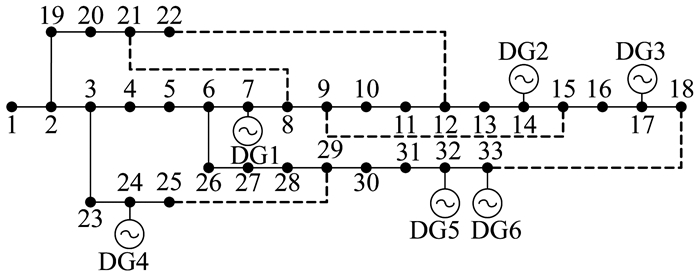
为验证所提方法的可行性, 本文采用改进IEEE 33节点系统为测试算例, 具体如图 1所示。
图 1中, 配电网系统额定电压为12.66 kV, 总负荷为3 715+j2 300 kVA。每条支路均装设分段开关, 虚线表示联络线路, 初始网络中联络开关均处于断开状态, 其他开关为闭合状态。节点7, 14, 17, 24, 32, 33分别接入DG1~DG6, 其中DG1和DG2为光伏电站, DG3和DG6为柴油发电机, DG4和DG5为风机。各DG的具体参数设置如表 1所示。各个负荷节点的等级、类型如表 2和表 3所示。设置网络损耗的权重为0.1, 灰狼算法的最大迭代次数为50。
表 1
DG系统参数
| 编号 | 接入位置 | DG类型 | DG额定容量/kW |
| DG1 | 7 | 光伏电站 | 800 |
| DG2 | 14 | 光伏电站 | 500 |
| DG3 | 17 | 柴油机 | 300 |
| DG4 | 24 | 风机 | 400 |
| DG5 | 32 | 风机 | 650 |
| DG6 | 33 | 柴油机 | 400 |
表 2
负荷等级及权重
| 负荷等级 | 负荷节点 | 负荷权重值 |
| 一级 | 4, 7, 14, 24, 32 | 100 |
| 二级 | 2, 6, 8, 15, 16, 17, 22, 23, 27, 29, 33 | 10 |
| 三级 | 其他节点 | 1 |
表 3
负荷类型
| 负荷类型 | 节点 |
| 政府、医疗负荷 | 4, 7, 14, 32 |
| 商业负荷 | 3, 9, 10, 11, 15, 19, 23, 26, 28, 29, 31 |
| 居民负荷 | 其他节点 |
| 可控负荷 | 18, 25, 30 |
4.2 算例结果分析
4.2.1 不同故障时刻恢复结果分析
设置故障时刻为9:00, 13:00, 20:00。故障位置在节点5至节点6的支路处。当故障发生时, 首先将故障点分段开关断开, 对故障支路进行隔离; 然后根据负荷在故障时段的需求值以及自身的负荷重要程度, 优先保证对重要负荷的供电。
各故障时刻的恢复结果如表 4所示。
表 4
各故障时刻的恢复结果
| 故障时刻 | 网络损耗/kW | 负荷恢复率/% | 失电负荷节点 | |
| 主网 | 孤岛 | |||
| 9:00 | 106.42 | 58.2 | 41.8 | 无 |
| 13:00 | 97.68 | 59.8 | 21.8 | 11, 27, 30, 31 |
| 20:00 | 93.83 | 49.2 | 34.0 | 10, 11, 15, 30 |
在9:00发生故障时, 由于此时段各失电负荷功率需求值较小, 且风能、光能都具有一定的输出功率值, 故通过整体寻优可以实现全部负荷恢复供电。此时段DG2, DG3, DG5, DG6形成一个大孤岛区域, 根据电源评价系数选取DG6作为孤岛的主电源。在13:00发生故障时, 此时段负荷功率需求值明显增大, 导致主网和孤岛的联合供电区域缩小, 此时孤岛区域为节点16, 17, 18, 32, 33, 不再包含DG2, 但此时段的一级负荷恢复率仍为100%。在20:00发生故障时, 此时段内光伏发电不再出力, 导致主网并入光伏发电系统后不能再提供恢复功率, 主网负荷恢复率有所减少, 但此时段内风机出力较大, 当风机并入孤岛时可增加一定的孤岛区域。
4.2.2 不同方案的故障恢复结果分析
为进一步验证本文所提故障恢复策略的优越性, 采用4种不同的恢复方案, 对2种配电网故障场景下的供电恢复结果进行比较分析。其中: 方案1采用本文所提方案, 利用主网和孤岛之间的两阶段供电恢复模型, 实现主网和孤岛联合恢复供电的整体最优; 方案2仅对配电网进行主网重构, 不考虑DG的孤岛运行; 方案3采用文献[8]方法, 将主网和孤岛划分为两个独立的子问题, 进行一次性的两阶段供电恢复; 方案4采用文献[19]方法, 基于混合整数二阶锥规划的配电网供电恢复。
场景1设故障发生时刻为9:00, 故障位置为节点5至节点6的支路。场景1下不同方案故障恢复结果如表 5所示。
表 5
场景1下不同方案故障恢复结果
| 方案 | 网络损耗/kW | 负荷恢复率/% | 失电负荷节点 | ||
| 全网 | 主网 | 孤岛 | |||
| 1 | 106.40 | 100.0 | 58.2 | 41.8 | 无 |
| 2 | 101.76 | 89.4 | 89.4 | 9, 30 | |
| 3 | 101.76 | 89.4 | 89.4 | 9, 30 | |
| 4 | 105.32 | 94.6 | 43.4 | 51.2 | 10 |
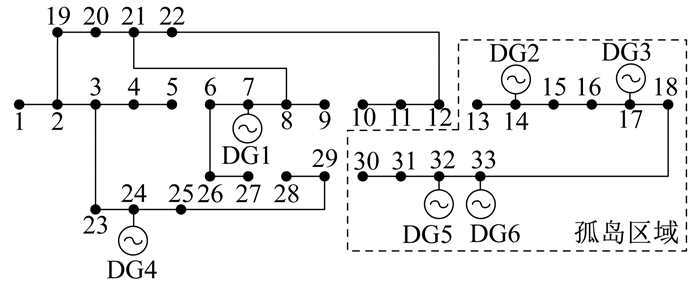
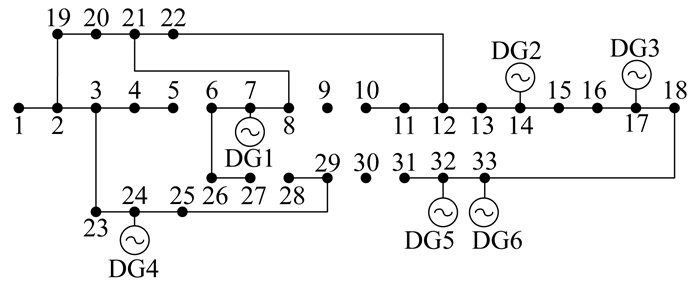
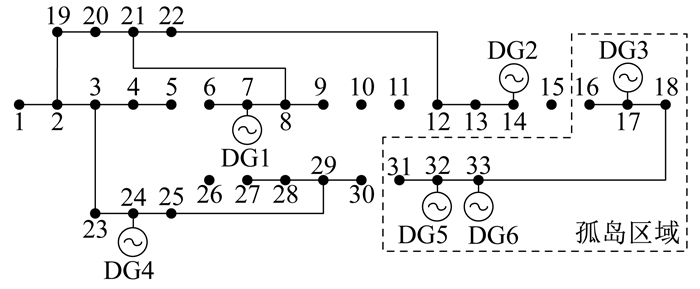
场景1下, 方案1, 2, 4故障恢复结果分别如图 2、图 3、图 4所示。
由表 5可知, 方案1可恢复全部负荷的供电, 更加优于方案2, 3, 4。方案3将主网和孤岛划分为两个独立的子问题进行求解, 未考虑两者之间关联性和配合性问题, 方案3的孤岛划分是针对方案2主网最优重构对应的甩负荷区域, 由方案2的主网最优重构图 3可知, 方案2对应的甩负荷区域内不存在可控DG, 无法形成孤岛对失电区域恢复供电, 因此方案3中的孤岛划分策略也就失去了意义, 故此场景下方案2、3的配电网恢复策略和结果相同。
由图 4可知, 方案4相比方案1故障的恢复更偏向于孤岛对失电负荷支撑能力, 因为方案4针对故障恢复时, 优先考虑的是孤岛最大化的恢复负荷, 然后将孤岛作为一个整体参与到主网重构之中。从结果分析中可以得出, 方案4能够实现最大化的孤岛恢复, 但孤岛和主网两者之间的配合性不足, 未能充分利用主网的恢复力, 导致负荷节点10未能恢复供电。综合分析表明本文所提的方案1能够增加主网和孤岛联合恢复供电的配合性, 实现两者的整体寻优。
场景2设故障发生时刻为20:00, 故障位置为节点5至节点6的支路。场景2下不同方案故障恢复结果如表 6所示。
表 6
场景2下不同方案的故障恢复结果
| 方案 | 网络损耗/kW | 负荷恢复率/% | 失电负荷节点 | |||
| 一级 | 二级 | 三级 | 全网 | |||
| 1 | 93.83 | 100 | 92.77 | 76.26 | 89.05 | 10, 11, 15, 26 |
| 2 | 84.14 | 100 | 71.08 | 60.31 | 76.45 | 10, 11, 15, 16, 17, 26, 27, 28 |
| 3 | 91.27 | 100 | 90.36 | 67.62 | 84.13 | 10, 11, 26, 27, 28 |
| 4 | 96.41 | 100 | 90.36 | 72.68 | 87.34 | 10, 26, 27, 31 |
场景2下方案1故障恢复结果如图 5所示。
由表 6可知, 方案1不仅全网恢复率最高, 而且二级、三级负荷恢复率都要优于方案2, 3, 4。方案3是在方案2的基础上进行孤岛划分, 由于方案2的主网重构目标是恢复负荷最大化, 使主网尽可能多地恢复重要负荷, 主网重构为保证一级负荷节点14, 32能恢复供电, 使重构方案向节点14, 32方向蔓延, 则导致了第二阶段的孤岛划分区域受到限制, 未能够充分利用孤岛内DG供电支持力。方案4优先考虑孤岛, 将DG2, DG3, DG5, DG6整合为一个大的孤岛区域, 充分发挥了孤岛的供电能力, 但也在一定程度上抑制了主网的重要负荷的支撑能力, 导致二级负荷节点27未能恢复供电。综合分析可知本文所提的方案1充分利用了孤岛和主网联合进行失电区域供电恢复, 实现了整体恢复方案的最优性。
5 结语
由于主网和DG的输出功率共同影响配电网的故障恢复策略, 因此本文提出了考虑主网和孤岛的两阶段配电网供电恢复方案。该方案考虑了DG的波动性, 建立了动态的孤岛划分策略和最优切负荷操作; 然后通过两阶段规划模型, 建立一阶段和二阶段相互联系的目标函数, 增加两者联合恢复供电的配合性。仿真结果表明, 本文所提方法实现了恢复系统失电负荷最大化, 充分利用了主网和孤岛对失电区域的支撑能力。
参考文献
-
[1]李振坤, 何苗, 苏向敬, 等. 基于生物体免疫机制的智能配电网故障恢复方法[J]. 中国电机工程学报, 2021, 41(23): 7924-7937.
-
[2]应宇辰, 王灿, 董庆国. 基于负荷综合权值的配电网孤岛划分策略[J]. 电网与清洁能源, 2021, 37(10): 91-97. DOI:10.3969/j.issn.1674-3814.2021.10.013
-
[3]闫涵, 王建华, 范须露, 等. 基于用户停电损失评估的有源配电网灾后供电恢复模型[J]. 电力系统自动化, 2022, 46(5): 31-42.
-
[4]谢云云, 杨正婷, 蔡胜, 等. 基于鲁棒模型预测控制的配电网供电恢复策略[J]. 电力系统自动化, 2021, 45(23): 123-131.
-
[5]李振坤, 周伟杰, 王坚敏, 等. 基于风光荷功率曲线的有源配电网动态孤岛划分方法[J]. 电力系统自动化, 2016, 40(14): 58-64.
-
[6]陈昕玥, 唐巍, 陈禹, 等. 基于机会约束规划含光伏发电的配电网故障恢复[J]. 电网技术, 2014, 38(1): 99-106.
-
[7]徐岩, 张荟, 孙易洲. 基于变异粒子群算法的主动配电网故障恢复策略[J]. 电力自动化设备, 2021, 41(12): 45-53.
-
[8]王红君, 陈智晴, 赵辉, 等. 考虑风光荷不确定性的配电网故障恢复策略[J]. 电网技术, 2022, 46(11): 4356-4364.
-
[9]陈文兴, 张沈习. 考虑孤岛划分与网络重构相配合的主动配电网故障恢复策略[J]. 水电能源科学, 2022, 40(1): 200-205.
-
[10]邢晓敏, 潘成琳, 李贻涛. 考虑孤岛与重构的配电网故障双层恢复策略[J]. 吉林电力, 2022, 50(5): 4-8.
-
[11]杨丽君, 高鹏, 王伟浩, 等. 考虑时间尺度的配电网故障恢复方法研究[J]. 太阳能学报, 2021, 42(1): 453-459.
-
[12]吴疆, 吕林, 黄媛, 等. 灾害全过程配电网弹性评估方法及提升策略[J]. 电力系统及其自动化学报, 2021, 33(3): 32-42.
-
[13]庞凯元, 王崇宇, 文福拴, 等. 主动配电网灵活孤岛划分与实时调度策略[J]. 电力系统自动化, 2022, 46(22): 13-24.
-
[14]刘礼邦, 武传涛, 随权, 等. 计及可控负荷参与的主动配电网动态恢复供电策略[J]. 电力系统保护与控制, 2020, 48(9): 27-35.
-
[15]李振坤, 魏砚军, 张智泉, 等. 有源配电网黑启动恢复供电辅助服务市场机制研究[J]. 中国电机工程学报, 2022, 42(18): 6641-6655.
-
[16]商皓钰, 刘天琪, 卜涛, 等. 计及风电与光伏并网的电力系统运行风险评估[J]. 现代电力, 2020, 37(4): 358-367.
-
[17]史训涛, 柯清派, 袁智勇, 等. 考虑光伏和负荷随机性的含柔性开关配电网故障重构[J]. 南方电网技术, 2020, 14(7): 56-61.
-
[18]赵超, 王斌, 孙志新, 等. 基于改进灰狼算法的独立微电网容量优化配置[J]. 太阳能学报, 2022, 43(1): 256-262.
-
[19]张盛, 汪李忠, 刘航, 等. 基于混合整数二阶锥规划的恢复供电策略[J]. 电网与清洁能源, 2022, 38(3): 32-41.