|
|
|
发布时间: 2024-02-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-09-20
基金项目: 上海市中央引导地方科技发展资金项目(YDZX20223100003002)
中图法分类号: TM614;TM712
文献标识码: A
文章编号: 2096-8299(2024)01-0051-07
|
摘要
电力负荷不确定性问题是需求响应不确定性问题的重要研究方向之一。准确、有效的电力系统负荷预测是保障电网安全、稳定运行和社会正常生产的重要前提。为了提高电力系统负荷预测的准确性, 提出了HI-Informer模型进行电力负荷预测。该模型通过最小二乘法将历史惯性(HI)模型和Informer模型融合。实验结果显示, HI-Informer模型在电力负荷预测中表现出色, 其预测结果与实际观测值高度吻合, 成功捕捉了电力负荷趋势和季节性变化。相比之下, 其他模型在某些情况下出现了明显的误差, 未能有效捕捉相同特征。
关键词
需求响应; 电力负荷; 长短期记忆; 历史惯性
Abstract
The study of power load uncertainty is one of the important research directions of demand response uncertainty. The accurate and effective forecasting of electrical system load is a crucial prerequisite for ensuring the safe and stable operation of the power grid and the normal functioning of society. To enhance the accuracy of load forecasting, this study proposes the HI-Informer model for electric load forecasting, which combines historical inertia modeling with the Informer model using the least squares method. The experimental results demonstrate that the HI-Informer model excels in electric load forecasting. Its predictions closely match the actual observed values and successfully capture the trends and seasonal variations in electrical load. In contrast, other models exhibit noticeable errors in certain scenarios and fail to effectively capture the same characteristics.
Key words
demand response; electric load; long short-term memory; historical inertia
需求响应是指电力市场用户响应市场价格信号或激励措施, 改变传统用电模式的市场参与行为。在电力现货市场竞争中引入需求响应, 对资源进行协调优化是适应电力现货市场发展的必然要求。科学、准确的电力负荷预测是优化调度方案和发电计划的基础。近年来, 大规模间歇性新能源发电系统并网, 新型负荷的广泛接入, 以及需求响应不确定性等问题, 给电力负荷带来了更高的随机性和动态性, 对电力负荷预测的准确性和时间尺度提出了更高的要求[1-6]。如何在长时间序列电力负荷预测中提高电力负荷预测模型的准确性, 是当前重要且新颖的一个研究方向。
常用的电力负荷预测分析方法主要分为两大类: 第1类是以数理统计为基础的传统负荷预测方法; 第2类是以深度学习为代表的智能负荷预测方法。第1类方法主要是根据历史负荷数据建立预测对象的函数模型。文献[7]采用优化后的差分整合移动平均自回归(Autoregressive Integrated Moving Average, ARIMA)模型进行电力负荷预测, 预测结果的准确度可以达到神经网络的预测水平, 但是时间序列方法对电力负荷的平滑性要求较高, 如果电力负荷受到其他不稳定因素的影响, 预测效果就达不到相应的精度, 甚至大打折扣。文献[8]基于灵敏度分析选择了多元非线性回归模型的关键变量, 获得了高精度的制冷负荷预测结果。为了提高预测精度, 文献[9]提出了一种由蚂蚁狮子优化器(1, 1)确定参数的滚动机构优化灰色模型, 并用电力负荷数据集进行验证。然而, 由于电力负荷的非线性特性, 第1类方法的预测精度较低。第2类方法是以深度学习为代表的智能负荷预测方法, 由于其强大的非线性拟合能力, 所以能够较好地完成电力负荷预测任务[10-12]。文献[13]将支持向量机(Support Vector Machine, SVM)用于电力负荷预测, 得到了比BP神经网络(Back Propagation Natural Network, BPNN)更好的预测结果。文献[14]提出了一种核组合SVM的预测模型, 与传统SVM模型相比, 预测精度得到了很大的提高。文献[15]开发了一种基于模糊逻辑的专家系统, 将其应用于电力负荷预测。文献[16-17]采用粒子群优化(Particle Swarm Optimization, PSO)算法对神经网络进行了优化, 解决了传统BPNN收敛速度较慢的难题。然而, 常用于电力负荷预测的递归神经网络(Recurrent Netural Network, RNN)由于点与点之间的路径较长, 故存在难以捕捉长时间序列模式的局限性。
RNN或长短期记忆(Long Short-Term Memory, LSTM)神经网络是该领域使用最广泛的深度学习模型之一, 原因是RNN或LSTM是一种以序列数据为输入并沿序列方向循环的神经网络, 在序列数据的非线性特征学习方面优于其他类型的神经网络。因此, 许多基于LSTM的短期负荷预测(Short Term Load Forecasting, STLF)模型被开发使用[18]。文献[19]提出了一种新的深度池化RNN模型, 用于家庭层面的STLF, 其在均方根误差(Root Mean Square Error, RMSE)方面优于经典深度RNN模型。文献[20]提出了一种基于LSTM的模型, 通过考虑季节、天数和间隔数据预测未来15 min的负荷。文献[21]结合LSTM和自注意力机制进行了日前住宅负荷预测。此外, 一些研究试图将RNN或LSTM与卷积神经网络(Convolutional Neural Network, CNN)相结合, 以提高负荷预测的精度。这些模型使用CNN提取局部特征, 然后将结果平面化并反馈到LSTM层。文献[22]提出了一种集成深度学习模型, 将CNN和LSTM结合起来用于设备级的STLF。文献[23]开发了一个使用CNN和双向LSTM的统一客户级STLF框架。这些模型的预测结果验证了CNN层能够从多个变量中提取有效特征, 从而提高基于RNN模型的负荷预测性能。
然而, 从时间序列的角度来看, LSTM不能保持长期记忆[24], 难以设计以长负荷序列为输入的基于RNN或LSTM的预测模型, 并且无法从长负荷序列数据中捕获长期依赖关系。最近, 基于注意力的深度学习模型, 在捕获长期依赖关系方面表现出比RNN或LSTM模型更好的性能[25]。但自注意力机制的时间复杂度和内存使用量为零(l2), 限制了其在长序列特征学习中的应用。为了解决这个问题, 文献[26]提出了一种高效的基于Transformer的Informer模型。它通过设计一种称为ProbSparse的自注意力机制, 将自注意力机制的复杂性降低到零(LlogL)。在这种机制中, 只考虑一部分主导查询并包括在注意力计算中。由于电力负荷消耗数据是一种长时间的周期序列, Informer的ProbSparse自注意力机制可能会忽略负荷曲线的周期性特征。为了解决这一问题, 本文提出了一种将Informer模型与历史惯性(Historical Inertia, HI)模型融合的HI-Informer模型, 并将HI-Informer模型与Informer模型、LSTM模型、RNN模型、多层感知(Maltilayer Perception, MLP)模型进行实验对比。实验结果表明, HI-Informer模型在电力负荷预测中表现出色, 负荷预测精度高于其他模型。
1 相关理论介绍
1.1 Informer模型简介
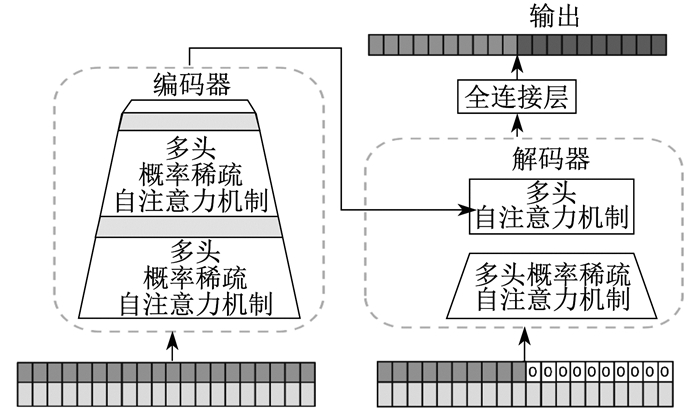
Transformer在捕获长期依赖关系方面显然比RNN具有更高的性能。然而, Transformer存在长输入序列下堆叠层的内存瓶颈、自注意力机制的二次计算复杂度高, 以及预测长输出时推理比较缓慢等问题。Informer模型通过改进Transformer结构, 解决了自注意力机制中的稀疏性问题: 首先, 采用稀疏自注意力机制, 压缩注意层卷积池, 降低时间复杂度和内存占用; 其次, 利用自注意力机制减少网络参数和维数, 接受长时间序列输入; 最后, 采用生成式解码器, 得到长时间序列的输出结果, 有效提高预测精度。Informer模型由编码器和解码器组成。其中, 编码器用来获取原始输入序列鲁棒性的长期依赖关系, 解码器进一步实现序列预测。Informer模型整体框架如图 1所示。
Informer模型编码器的输入由t个特征变量、t个局部时间戳、t个全局时间戳组成。Q, K, V为输入特征变量线性转换后得到的3个相同大小的查询矩阵、键矩阵和值矩阵。Q∈RLQ×d, K∈RLK×d, V∈RLV×d, d为输入维度, LQ, LK, LV分别为Q, K, V的行维度。多头概率稀疏自注意力机制模型O的计算公式为
| $\begin{array}{r} O=\operatorname{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})= \\ \boldsymbol{V} \cdot \operatorname{softmax}\left(\frac{\overline{\boldsymbol{Q}} \times \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d}}\right) \end{array}$ | (1) |
式中: Attention(·)——注意力函数;
Q——对 Q按概率进行减薄后得到的矩阵;
softmax(·)——激活函数。
为了压缩特征维数并提取优势注意, 编码器采用自注意力蒸馏技术, 通过卷积和最大池化减少维数和网络参数。经过多次多头概率稀疏自注意力和自注意力蒸馏, 编码器最终输出特征映射。
从j层到j+1层的蒸馏过程为
| $L_{j+1}^t=\max \operatorname{Pool}\left\{\operatorname{ELU}\left[\operatorname{Convld}\left(\left[L_j^t\right]_{\mathrm{AB}}\right)\right]\right\}$ | (2) |
式中: Ljt, Lj+1t——第j层和第j+1层注意力模块输入;
max Pool(·)——最大池化函数;
ELU(·)——激活函数;
Convld(·)——一维卷积函数;
[]AB——自注意力模块。
为了一次性输出所有预测结果, Informer模型解码器采用并行生成解码器机制。其中, 输入由t-k个特征变量、k个占位符0以及对应的t个局部时间戳和t个全局时间戳组成。通过带掩码的多头概率稀疏自注意力机制运算后, 利用编码器输出的特征图进行多头自注意力机制运算。最后, 通过全连接层调整数据输出的维度, 可以一次性输出研究者想要的所有预测结果。其中, t代表一个输出长度, k代表一个预测长度。
1.2 HI模型简介
传统的时间序列预测方法通常关注时间序列数据中的趋势、周期性和季节性等因素。然而, 时间序列中的历史信息本身包含有价值的信息。这种历史信息的保持和延续被称为HI。本文引入HI模型[27]与Informer模型结合。HI模型的具体原理如下。
时间预测序列: 在时间t, 给定一个输出长度Lx的时间序列X(t)为
| $\boldsymbol{X}(t)=\left\{\boldsymbol{X}_1(t), \boldsymbol{X}_2(t), \boldsymbol{X}_3(t), \cdots, \boldsymbol{X}_{L_{\mathrm{x}}}(t)\right\}$ | (3) |
式中: Xi(t)——在第i个时间戳观察到的单变量(dx=1)或多变量(dx>1), i=1, 2, 3, …, Lx。
| $\begin{aligned} & \boldsymbol{X}_i(t)= \\ & {\left[x_{i, 1}(t), x_{i, 2}(t), x_{i, 3}(t), \cdots, x_{i, d_{\mathrm{x}}}(t)\right] \in R^{d_{\mathrm{x}}}} \end{aligned}$ | (4) |
时间序列预测目标是提前Δ步预测对应长度Ly的序列Y(t), 为
| $\boldsymbol{Y}(t)=\left\{\boldsymbol{Y}_1(t), \boldsymbol{Y}_2(t), \boldsymbol{Y}_3(t), \cdots, \boldsymbol{Y}_{L_{\mathrm{y}}}(t)\right\}$ | (5) |
式中: Yi(t)=
| $ \left[y_{i, 1}(t), y_{i, 2}(t), y_{i, 3}(t), \cdots, y_{i, d_{\rm{y}}}(t)\right] \in R^{d_{\rm{y}}} 。$ |
HI以输入序列X(t)的子序列预测长度Ly为预测结果。HI作用示意如图 2所示。
规范的数学表示为
| $\begin{aligned} & \boldsymbol{Y}(t)= \\ & \left\{\boldsymbol{X}_{L_{\mathrm{x}}-L_{\mathrm{x}}+1}(t), \boldsymbol{X}_{L_{\mathrm{x}}-L_{\mathrm{x}}+2}(t), \boldsymbol{X}_{L_{\mathrm{x}}-L_{\mathrm{x}}+3}(t), \cdots, \boldsymbol{X}_{L_{\mathrm{x}}}(t)\right\} \end{aligned}$ | (6) |
2 HI-Informer电力负荷预测模型
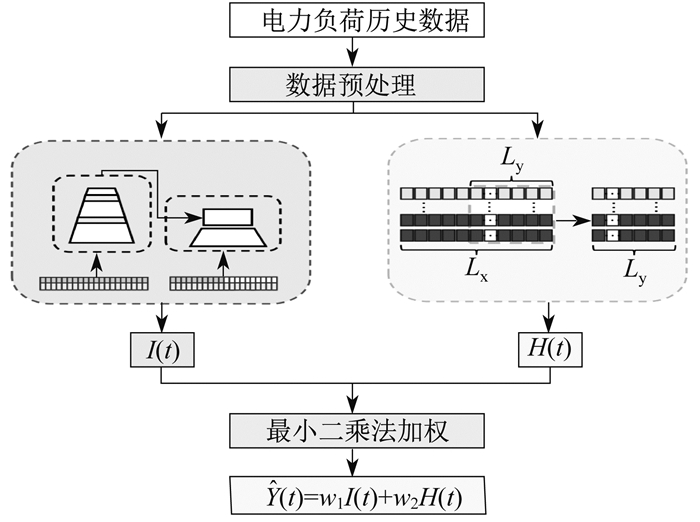
电力负荷数据是一系列复杂的不连续时间序列, 受多种环境因素的影响。对于电力负荷数据预测, 首先, 使用Informer模型提取序列特征并预测未来的电力负荷数据; 然后, 使用HI模型预测未来序列; 最后, 使用最小二乘法拟合Informer和HI模型的权重系数, 使得混合HI-Informer模型的预测结果与实际数据之间的差异最小。将Informer模型的输出序列定义为I(t), HI模型的输出顺序定义为H(t), 最小二乘法将两者的权重系数分配为w1, w2。HI-Informer模型框架如图 3所示。
预测模型序列
| $\hat{Y}(t)=w_1 I(t)+w_2 H(t)$ | (7) |
| $ w_1+w_2=1$ | (8) |
为了使HI-Informer模型的预测结果与实际结果之间的差异最小化, 将距离函数定义为预测结果与实际结果之间的双范数, 并选择合适的权重系数w1和w2使双范数最小化。双范数是w1和w2的函数, i∈T表示计算权系数的时间集, T为验证集时间的集合。双范数最小化的计算公式为
| $\begin{gathered} \min f\left(w_1, w_2\right)=\|\hat{Y}-Y\|= \\ \sum\limits_{i \in T}\left(\hat{y}_i-y_i\right)^2= \\ \ \ \ \ \ \ \ \ \ \sum\limits_{i \in T}\left(w_1 I_i+w_2 H_i-y_i\right)^2 \end{gathered}$ | (9) |
式中:
Y——真实序列;
Ii——第i个时间戳的输出值;
Hi——HI模型第i个时间戳的输出值。
为了更好预测未来数据, 将训练集拆分为新的训练集和验证集, 分别对w1和w2求式(7)的偏导数, 得到:
| $\frac{\partial f\left(w_1, w_2\right)}{\partial w_1}=\sum\limits_{i \in T} 2\left(w_1 I_i+w_2 H_i+y_i\right) I_i=0$ | (10) |
| $\frac{\partial f\left(w_1, w_2\right)}{\partial w_2}=\sum\limits_{i \in T} 2\left(w_1 I_i+w_2 H_i-y_i\right) H_i=0$ | (11) |
| $w_1+w_2=1$ | (12) |
权重系数w1和w2可由式(8)~式(10)联立求得, 为
| $\left\{\begin{array}{r} w_1=\frac{\sum\limits_{i \in T}\left(y_i-H_i\right) I_i}{\sum\limits_{i \in T}\left(I_i-H_i\right) I_i} \\ w_2=\frac{\sum\limits_{i \in T}\left(I_i-y_i\right) I_i}{\sum\limits_{i \in T}\left(I_i-H_i\right) I_i} \end{array}\right.$ | (13) |
通过最小二乘法将HI模型和Informer模型的预测结果进行加权融合, 使其能够显著减小预测误差, 提高整体预测的可靠性和准确性, 增加系统的稳定性, 降低对特定模型的依赖, 从而在不同情况下保持高性能。此外, 加权融合方法非常灵活, 可以根据任务需要进行定制。
3 实验过程与分析
3.1 数据准备
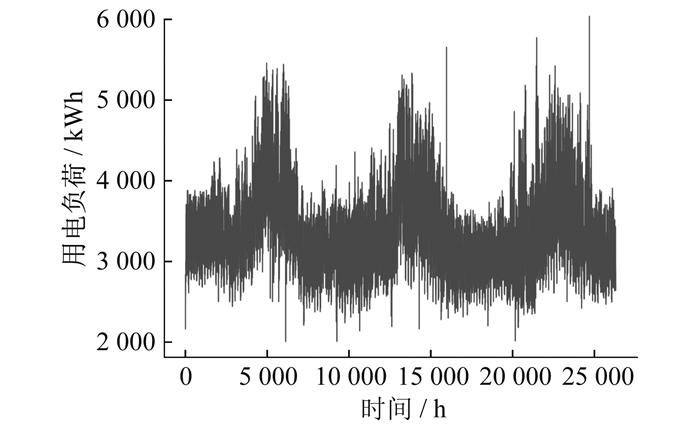
实验数据来自新加坡的电力负荷数据。数据包含2020年1月1日至2022年12月31日321个用户的用电量, 采集间隔为1 h, 数据总数为2.7万个。某用户历史用电负荷如图 4所示。
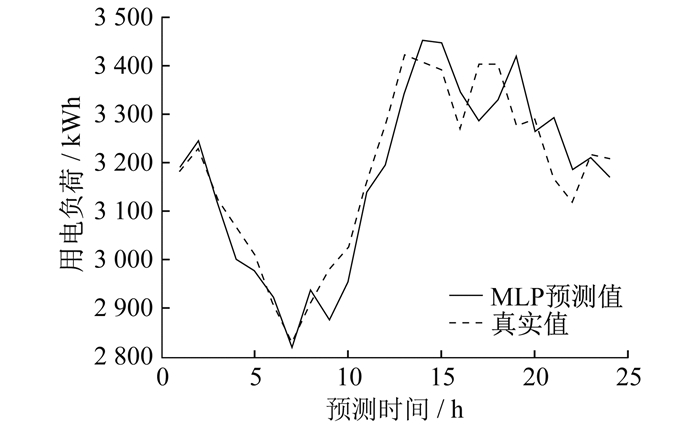
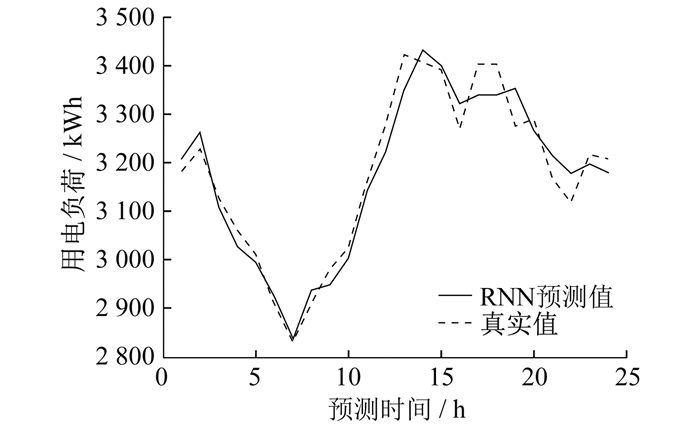
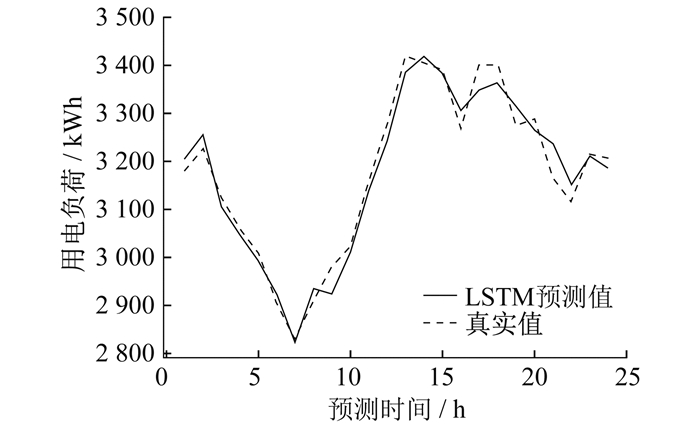
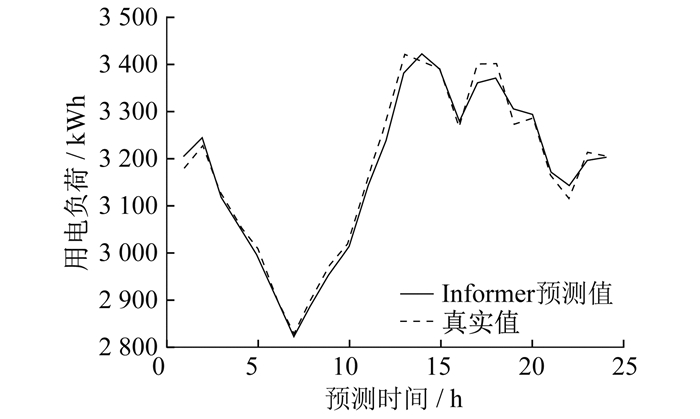
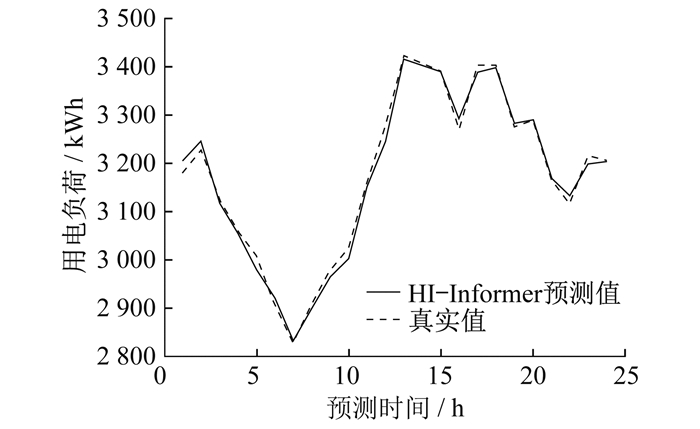
3.2 实验结果对比
3.3 实验结果分析
在本次研究中, 使用平均绝对误差EMA、均方误差EMS、对称平均绝对百分比误差ESMAP和运行时间评估模型的预测性能。EMA是回归任务的基本评价指标。相比EMA, EMS对异常值更为敏感。ESMAP是一种基于百分比误差的精度度量, 能更好地评价模型预测的准确性。具体定义为
| $E_{\mathrm{MA}} =\frac{1}{N} \sum\limits_{n=1}^N\left|\hat{y}_n-y_n\right| $ | (14) |
| $E_{\mathrm{MS}} =\frac{1}{N} \sum\limits_{n=1}^N\left(\hat{y}_n-y_n\right)^2 $ | (15) |
| $E_{\mathrm{SMAP}} =\frac{100 \%}{N} \sum\limits_{i=0}^N \frac{\left|y_i-\hat{y}_i\right|}{\left|y_i\right|}$ | (16) |
式中:
yn——预测流量值;
N——预测总数, 即预测序列长度。
在相同数据集上, 将本文提出的HI-Informer模型与Informer模型、LSTM模型、RNN模型、MLP模型进行对比实验。模型评价结果如表 1所示。
表 1
模型评价结果
| 模型 | EMS | ESMAP | EMA |
| MLP | 428 | 0.000 040 | 17.026 4 |
| RNN | 1 007 | 0.000 900 | 27.167 7 |
| LSTM | 1 689 | 0.000 159 | 35.676 5 |
| Informer | 4 570 | 0.004 390 | 54.759 7 |
| HI-Informer | 266 | 0.000 020 | 12.173 9 |
通过比较不同模型误差值发现, HI-Informer模型表现最佳, 其平均预测误差最小。这表明HI-Informer模型在处理电力负荷预测任务时具有明显的优势。
4 结语
本文进行了电力负荷预测任务的对比实验, 特别关注了HI-Informer模型在电力负荷预测中的性能。实验结果表明, HI-Informer模型在电力负荷预测任务中表现出色, 在平均绝对误差EMA、均方误差EMS、对称平均绝对百分比误差ESMAP上表现突出, 具有更低的误差值。这表明HI-Informer模型在处理长时间序列数据方面具有优越性, 能够更好地捕捉电力负荷趋势和季节性变化。
参考文献
-
[1]范士雄, 李立新, 王松岩, 等. 人工智能技术在电网调控中的应用研究[J]. 电网技术, 2020, 44(2): 401-411.
-
[2]李瑞津, 刘斌, 张学敏, 等. 基于改进LSTM的变电站铅酸电池寿命预测[J]. 电池, 2020, 50(6): 560-564.
-
[3]刘成龙, 高旭, 曹明. 基于VMD和BA优化随机森林的短期负荷预测[J]. 中国测试, 2022, 48(4): 159-165.
-
[4]张宇帆, 艾芊, 林琳, 等. 基于深度长短时记忆网络的区域级超短期负荷预测方法[J]. 电网技术, 2019, 43(6): 1884-1892.
-
[5]李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364.
-
[6]孙庆凯, 王小君, 张义志. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63-70.
-
[7]LEE C M, KO C N. Short-term load forecasting using lifting scheme and ARIMA models[J]. Expert Systems with Applications, 2011, 38(5): 5902-5911. DOI:10.1016/j.eswa.2010.11.033
-
[8]FAN C, DING Y. Cooling load prediction and optimal operation of HVAC systems using a multiple nonlinear regression model[J]. Energy and Buildings, 2019, 197: 7-17. DOI:10.1016/j.enbuild.2019.05.043
-
[9]KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information Processing Systems, 2012, 25: 6-15.
-
[10]JINGBO M, HONGGENG Y. Application of adaptive Kalman filtering in short-term load forecasting of power systems[J]. Power Grid Technol, 2005, 29: 75-79.
-
[11]XU W, PENG H, ZENG X, et al. A hybrid modelling method for time series forecasting based on a linear regression model and deep learning[J]. Applied Intelligence, 2019, 49: 3002-3015. DOI:10.1007/s10489-019-01426-3
-
[12]LIU L, LIU J, ZHOU Q, et al. An SVR-based machine learning model depicting the propagation of gas explosion disaster hazards[J]. Arabian Journal for Science and Engineering, 2021, 46: 10205-10216. DOI:10.1007/s13369-021-05616-5
-
[13]YE N, LIU Y, WANG Y. Short-term power load forecasting based on SVM[C]//World Automation Congress 2012. Shanghai, China: IEEE, 2012: 47-51.
-
[14]CHE J X, WANG J Z. Short-term load forecasting using a kernel-based support vector regression combination model[J]. Applied Energy, 2014, 132: 602-609. DOI:10.1016/j.apenergy.2014.07.064
-
[15]HSU Y Y, HO K L. Fuzzy linear programming: an application to short-term load forecasting[J]. Gerneration Transmission Distribution, 1992, 139: 471-477. DOI:10.1049/ip-c.1992.0066
-
[16]ZHAO Y P, SHENG Z L, HONG Z, et al. The application of the PSO based BP network in short-term load forecasting[J]. Physics Procedia, 2012, 24: 626-632. DOI:10.1016/j.phpro.2012.02.092
-
[17]BASHIR Z A, EL HAWARY M E. Applying wavelets to short-term load forecasting using PSO-based neural networks[J]. IEEE Transactions on Power Systems, 2009, 24(1): 20-27. DOI:10.1109/TPWRS.2008.2008606
-
[18]KONG W, DONG Z Y, HILL D J, et al. Short-term residential load forecasting based on resident behaviour learning[J]. IEEE Transactions on Power Systems, 2017, 33(1): 1087-1088.
-
[19]SHI H, XU M, LI R. Deep learning for household load forecasting—a novel pooling deep RNN[J]. IEEE Transactions on Smart Grid, 2017, 9(5): 5271-5280.
-
[20]BEDI J, TOSHNIWAL D. Deep learning framework to forecast electricity demand[J]. Applied Energy, 2019, 238: 1312-1326.
-
[21]ZHANG J, ZHANG H, DING S, et al. Power consumption predicting and anomaly detection based on transformer and K-means[J]. Frontiers in Energy Research, 2021, 9: 77-95.
-
[22]SHARDA S, SINGH M, SHARMA K. A complete consumer behaviour learning model for real-time demand response implementation in smart grid[J]. Applied Intelligence, 2022, 52(1): 835-845.
-
[23]VNAL F, ALMALAQ A, EKICI S. A novel load forecasting approach based on smart meter data using advance preprocessing and hybrid deep learning[J]. Applied Sciences, 2021, 11(6): 27-42.
-
[24]ZHAO J, HUANG F, LV J, et al. Do RNN and LSTM have long memory?[C]//International Conference on Machine Learning. Nanjing, China: PMLR, 2020: 11365-11375.
-
[25]VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[J]. Advances in Neural Information Processing Systems, 2017, 30: 26-37.
-
[26]ZHOU H, ZHANG S, PENG J, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[C]//Proceedings of the Conference on Artificial Intelligence. Beijing, China: AAAI, 2021: 11106-11115.
-
[27]CUI Y, XIE J, ZHENG K. Historical inertia: a neglected but powerful baseline for long sequence time-series forecasting[C]//Proceedings of the 30th ACM International Conference on Information & Knowledge Management. Beijing, China: IEEE, 2021: 2965-2969.