|
|
|
发布时间: 2024-04-28 |
智能设备与测量 |
|
|
|
收稿日期: 2023-11-28
中图法分类号: U221
文献标识码: A
文章编号: 2096-8299(2024)02-0143-07
|
摘要
钢轨对排流网的过渡电阻是影响杂散电流的最主要因素。为了快速测量过渡电阻,根据钢轨中的波过程和快速傅里叶变换原理,提出了利用冲击电压源的新型测量方法。首先,基于ATP-EMTP软件搭建钢轨模型进行仿真,验证了冲击法的有效性;然后,结合现场实测钢轨对排流网过渡电阻的数据,进一步验证了冲击法的可靠性和准确性。
关键词
轨道交通; 快速傅里叶变换; 冲击电压; 过渡电阻; ATP-EMTP软件; 杂散电流
Abstract
The transition resistance of the rail to the discharge network is the most important factor affecting the stray current. In order to quickly measure the transition resistance, based on the fast Fourier transform and the wave process in the rail, a new measurement method using the impulse voltage source is proposed. Firstly, based on ATP-EMTP software, the rail model is constructed for simulation to verify the validity of the inrush method, and then combined with the field measurement of the transition resistance of the rail to the discharge network, the reliability and accuracy of the impulse method is further verified.
Key words
rail transit; fast Fourier transform; impulse votage; transition resistors; ATPEMTP software; stray current
目前,世界各地均在发展轨道交通,东京、莫斯科、纽约等国际大都市均有发达的轨道交通网络系统。我国1953年开始建设第一条轨道交通线路——北京地铁1号线,并于1971年开通运营。之后天津、上海、广州、南京等城市也开始逐渐发展,与此同时,轨道交通直流牵引系统所引发的杂散电流问题也受到了广泛的关注。
直流牵引系统是指牵引变电站将1 500 V或750 V的低压直流电经馈电线传输到接触网,接触网经受电弓传输到机车上供机车使用,然后经回流轨和回流线回到牵引变电所的负极。
为了节省建造成本和降低施工难度,全世界大部分国家采用走行轨作为回流轨,大部分电流通过走行轨可以回到牵引变电所的负极,但是由于经过长时间的运行产生磨损以及隧道内潮湿漏水等因素,走行轨与大地之间无法实现完全绝缘,因此会发生部分电流泄漏现象,从而产生杂散电流。杂散电流经过地下无规律的流动,部分能够经过排流网回流到排流柜,然后到达牵引变电所的负极,但是也仍有一小部分无法回流到走行轨,最终流向金属管道。这不仅会破坏附近的埋地金属,还会干扰附近信息设备和精密仪器的通信,严重时还会危害人身安全。
钢轨对排流网的过渡电阻是影响杂散电流的最主要因素。目前,国内外诸多学者对地铁过渡电阻进行了广泛深入的研究。林炎华[1]在杂散电流分布路径的理论基础上,利用CDEGS软件搭建了地铁杂散电流分布模型,并在建模过程中提出了利用电缆外覆绝缘层等效钢轨绝缘垫过渡电阻的计算方法。朱峰等人[2]利用CDEGS软件进行轨地杂散电流建模仿真,讨论在不同区间过渡电阻值下杂散电流分布和轨电位变化情况,研究结果表明过渡电阻与钢轨导体绝缘层电阻率呈线性关系。CHARALAMBOUS C A[3]着重分析了影响轨排过渡电阻的主要因素,建立了地铁杂散电流仿真模型,并详细分析了钢轨扣件对地铁杂散电流的影响。蔡力等人[4]针对3种典型的地铁过渡电阻状态:新建线路验收限值(15 Ω·km)、已运行线路限值(3 Ω·km)和线路不良状态(0.5 Ω·km),对在机车运行时沿线的轨电位和杂散电流分布进行了数值计算和模拟仿真,研究认为:钢轨对排流网过渡电阻值越小,钢轨泄漏的杂散电流越大;土壤电阻率为100 Ω·m、过渡电阻为0.5 Ω·km时,钢轨最严重部分损失占33[%],年腐蚀量达到203.62 g/m。LEE C H等人5分析并采用了经二极管接地的方案,减小了轨道建设运行中的杂散电流,并取得了较好的效果。卢昱瑾[6]研究了基于粒子群优化算法的神经网络过渡电阻预测,将轨电位、轨电流,以及钢轨纵向电阻、轨地过渡电阻、土壤混凝土温度湿度等因素都考虑在内,综合分析后建立了最佳的过渡电阻预测模型。胡传等人[7]分析了现有的过渡电阻测量方法及误差,进一步研究了过渡电阻与杂散电流的关系,并给出一系列减少杂散电流、增大过渡电阻的建议和措施。
本文提出了一种利用冲击电压源测量地铁过渡电阻的新型方法,利用电力仿真软件ATPEMTP搭建钢轨模型并进行仿真。同时,在上海某地铁线路进行传统直流法和本文提出的新型冲击法对比实验,分析现场实测结果,验证冲击法的应用可行性。
1 过渡电阻测量原理
1.1 直流法测量原理
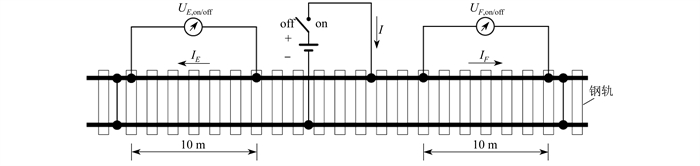
现阶段的过渡电阻测量方案主要按照标准GB/T 28026.2—2018《轨道交通地面装置电气安全、接地和回流第2部分:[直流牵引供电系]统杂散电流的防护措施》的要求8。钢轨纵向电阻测量原理如图 1所示。
图 1中,I为注入电流,UE、UF、IE、IF分别为E段和F段钢轨的电压和电流,下标on、off分别表示在注入和不注入电流时钢轨的电压降。10 m钢轨的纵向电阻R10的计算公式为
| $ R_{10}=\frac{\left(U_{E, {\text { on }}}-U_{E, {\text { off }}}\right)+\left(U_{F, {\text { on }}}-U_{F, {\text { off }}}\right)}{I} $ | (1) |
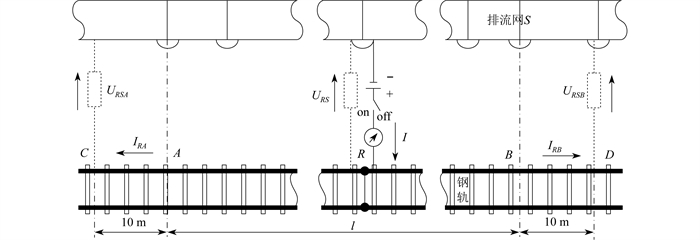
传统直流法测量钢轨对排流网过渡电阻原理如图 2所示。
图 2中:A点和B点距离电流注入点R点50 m左右;l为被测量区段的长度,约为0.1 km;AC和BD两段钢轨均为10 m,其纵向电阻均为R10;IRA、IRB为被测量区段的A点、B点末端流出电流;URS为电流注入点R点钢轨对排流网S的电压;URSA、URSB分别为被测量区段的A点和B点末端钢轨对排流网S的电压。
被测量区段的A点、B点末端流出电流IRA和IRB的计算公式为
| $ I_{R A}=\frac{\Delta U_{A C}}{R_{10}} $ | (2) |
| $ I_{R B}=\frac{\Delta U_{B D}}{R_{10}} $ | (3) |
| $ \Delta U=U_{{\text {on }}}-U_{{\text {off }}} $ | (4) |
式中:UAC,UBD——AC和BD段钢轨的电压降。
分别记录3次注入电流前后的UAC、UBD、URSA、URSB、URS、I。将3次检测结果计算平均值并记录。钢轨对排流网过渡电阻Rg的计算公式为
| $ R_{{\mathrm{g}}}=l \times \frac{\Delta U_{R S}+\Delta U_{R S A}+\Delta U_{R S B}}{3\left(I-I_{R A}-I_{R B}\right)} $ | (5) |
由于钢轨纵向电阻较小,所以UAC和UBD都是mV级,钢轨上残留的电压会对实验结果有所影响,导致过渡电阻的计算结果产生误差。测量前现场布线,需要多名工作人员进行同步读数,整个测量过程步骤繁杂,工作量巨大,测量结果也会因人工读数而增大误差[9]。
1.2 冲击法测量原理
1.2.1 钢轨中的波过程
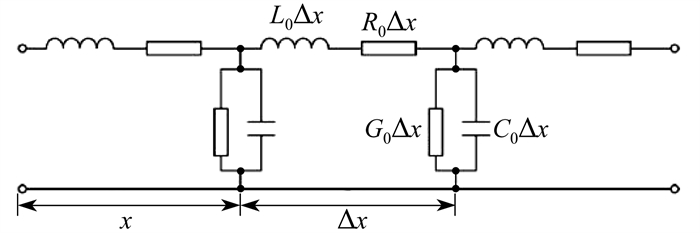
由文献[10]可知,钢轨可看作传输线模型,钢轨对排流网分布参数模型如图 3所示。其中,x为电压行波沿钢轨流动所经过的距离,Δx为极短的一段距离,R0为单位长度钢轨纵向电阻,L0为单位长度钢轨电感,C0为单位长度钢轨对排流网电容,G0为单位长度钢轨对排流网导纳,G0的倒数即钢轨对排流网的过渡电阻。
当电压行波在钢轨上传播时,由于R0和G0的存在,将有一部分波的能量转化为热能而耗散,导致波的衰减和变形。
如果钢轨参数满足无畸变线的条件,即R0/L0 = G0/C0,那么从均匀长线方程出发,可求得电压行波的衰减规律如下[11]:
| $ U_x=U {\mathrm{e}}^{-\frac{1}{2}\left(\frac{R_0}{L_0}+\frac{G_0}{C_0}\right) t}=U {\mathrm{e}}^{-\frac{1}{2}\left(\frac{R_0}{Z}+G_0 Z\right) x} $ | (6) |
式中:Ux——电压行波流过距离x后的幅值,V;
U——电压行波的原始幅值,V;
t——电压行波沿钢轨流动所经过的时间,s;
Z——钢轨波阻抗,Ω。
由式(6)可知,电压行波的幅值按指数规律衰减。
1.2.2 快速傅里叶变换
模拟信号x(t)连续傅里叶变换为
| $ X(\omega)=\int_{-\infty}^{+\infty} X(t) {\mathrm{e}}^{-{\mathrm{j}} \omega {\mathrm{t}}} {\mathrm{d}} t $ | (7) |
x(t)经过T个抽样周期后变为x(nT)。设x(n)为N点有限长序列。其离散傅里叶变换(Discrete Fourior Transform,DFT)为
| $ \begin{gathered} X(k)=\operatorname{DFT}[X(n)]=\sum\limits_{n=0}^{N-1} X(n) W_N^{n k}=\sum\limits_{n=0}^{N-1} X(n) {\mathrm{e}}^{-{\mathrm{j}} \frac{2 \pi}{N} n k} \\ k=0, 1, 2, \cdots, N-1 \end{gathered} $ | (8) |
式中:DFT(·)——离散傅里叶变换函数。
由于复数运算可以通过实数运算来完成,且x(n)、WNnk、x(k)都是复数,因此式(8)可以写成
| $ \begin{aligned} X(k)= & \sum\limits_{n=0}^{N-1} X(n) W_N^{n k}= \\ & \sum\limits_{n=0}^{N-1}\left\{\left\{\operatorname{Re}[X(n)] \operatorname{Re}\left(W_N^{n k}\right)-\operatorname{Im}[X(n)] \operatorname{Re}\left(W_N^{n k}\right)\right\}+\right. \\ & \left.{\mathrm{j}}\left\{\operatorname{Re}[X(n)] \operatorname{Im}\left(W_N^{n k}\right)+\operatorname{Im}[X(n)] \operatorname{Re}\left(W_N^{n k}\right)\right\}\right\} \end{aligned} $ | (9) |
又因为WNnk具有对称性、周期性,因此可得
| $ W_N^{n(N-k)}=W_N^{(N-n) k}=W_N^{-n k} $ | (10) |
| $ W_N^{\frac{N}{2}}=-1 $ | (11) |
| $ W_N^{\left(k+\frac{N}{2}\right)}=-W_N^k $ | (12) |
通过式(10)至式(12)简化,使DFT运算量大大减小[12]。
计算任务通常需要借助计算机进行处理,在执行复杂的傅里叶变换时,可能导致计算机功耗升高。然而,由于快速傅里叶变换对计算性能要求较低且具有高效的运算速度,因此在生产和生活中得到广泛应用。
1.2.3 过渡电阻计算原理
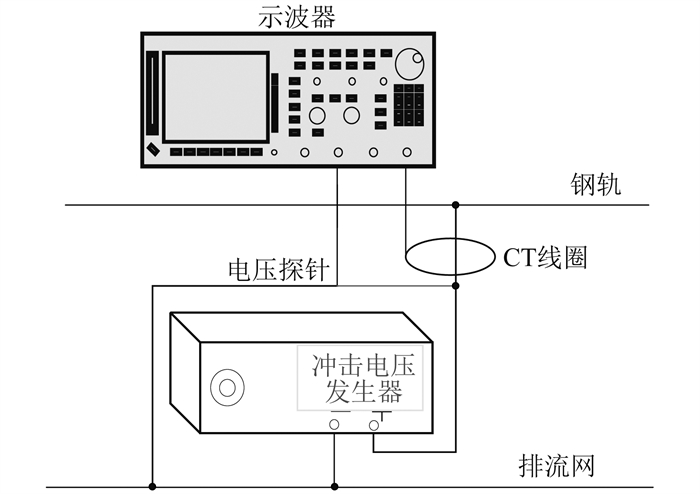
利用冲击法测量钢轨对排流网过渡电阻原理如图 4所示。冲击电压源正负极分别与钢轨和排流网相连,并且通过电压探针测量冲击电压信号,通过电流互感器(Current Transformer,CT)线圈测量冲击电流信号。
将冲击电压信号和首端测得的冲击电流信号进行快速傅里叶变换,得到其直流分量U0和I0。仅考虑U0和I0作用时,只需考虑整个电路中的阻性负载,可忽略感性负载和容性负载。
我国地铁轨道一般采用P60和P65两种型号的钢轨。本文选用P60型号钢轨,其单位长度钢轨纵向电阻R0为0.04 Ω/km,可忽略不计[],因此钢轨对排流网过渡电阻Rg的计算式为13
| $ R_{{\mathrm{g}}}=\frac{U_0}{I_0} \cdot \frac{\bar{l}}{1000} $ | (13) |
式中:U0——冲击电压直流分量,V;
I0——冲击电流直流分量,A;
l——电压行波在钢轨上的传播距离。
2 仿真过程及结果分析
2.1 仿真模型和参数设置
在建立钢轨仿真模型时,需要考虑模型的分段长度。较小的分段长度意味着更准确的计算结果,并更符合实际情况。然而,增加分段数会增加仿真模块和数据点,导致计算速度变慢。此外,由于导体仿真参数的计算基于多个假设,分段数增加会带来积累误差的问题。另一方面,较少的分段数会降低仿真模型的精确度,且无法有效代替轨道电路模型,而只能近似为集中参数电路。
在本文的仿真分析中,每个分段长度应满足小于λ/10且大于r的条件。其中,λ表示雷电脉冲作用在轨道上时雷电波形的最短波长,r表示钢轨的等效半径。由文献[14]可知,雷电波形的能量主要集中在几千赫到几十万赫的频率范围内,并且雷电波形的频率f低于1 MHz。已知电磁波在真空中传播的速度c为3.0×108 m/s,根据波长公式c=λf,雷电波形的波长λ大于300 m,因此选择的分段长度应小于30 m,以确保模型的准确性。
由电磁场理论可知,单位长度钢轨电感L0和单位长度钢轨对排流网电容C0的计算公式如下:
| $ L_0=\frac{\mu_0 \mu_{{\mathrm{r}}}}{2 \pi} \ln \frac{2 h}{r} $ | (14) |
| $ C_0=\frac{2 \pi \varepsilon_0 \varepsilon_{{\mathrm{r}}}}{\ln 2 h / r} $ | (15) |
式中:μ0——真空磁导率,取4π×10-7 H/m;
μr——相对磁导率,一般情况下取1;
h——钢轨与地面的距离,m;
ε0——真空或气体的介电常数,取8.854 187 817×10-12 F/m;
εr——相对介电常数,如周围媒质为空气,εr≈1。
其中,钢轨的等效半径r为0.05 m,钢轨与地面的距离h为0.15 m,代入式(14)和式(15)可得单位长度钢轨电感L0为0.36 mH/km,单位长度钢轨对排流网电容C0为3×10-9 F/km。单位长度钢轨纵向电阻R0取0.04 Ω/km,钢轨对排流网过渡电阻Rg取10 Ω·km。
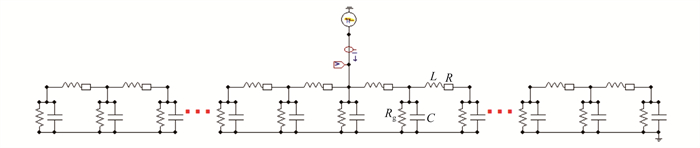
基于以上分析,在ATP-EMTP软件中搭建的钢轨π型仿真模型如图 5所示。其中,L为钢轨电感,R为钢轨纵向电阻,C为钢轨对排流网电容,每一小段长度取10 m,共30 km。
2.2 仿真结果分析
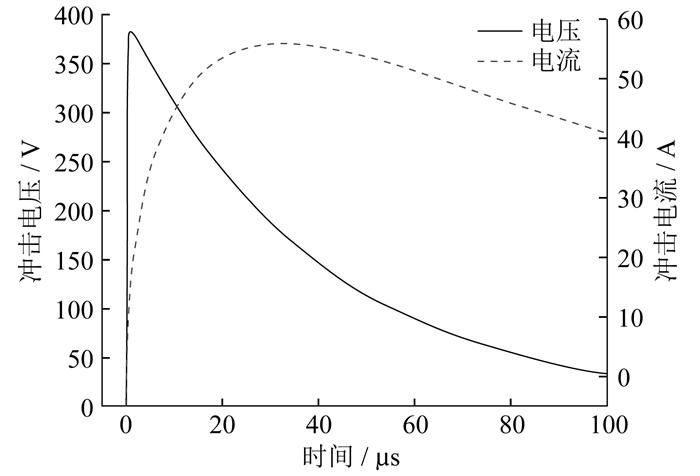
在钢轨模型的中间注入1.5/20 μs、幅值为380 V的冲击电压,测得注入端冲击电流和冲击电压波形如图 6所示。
通过对冲击电压及冲击电流信号快速傅里叶变换,可得冲击电压直流分量U0为31.54 V,冲击电流直流分量I0为27.67 A。
在仿真模型中,测得与注入点的距离对应的钢轨电位如表 1所示。
表 1
仿真模型中与注入点的距离对应的钢轨电位
| 与注入点的距离/m | 钢轨电位/V |
| 0 | 380 |
| 200 | 272 |
| 500 | 192 |
| 1 000 | 118 |
| 2 000 | 50 |
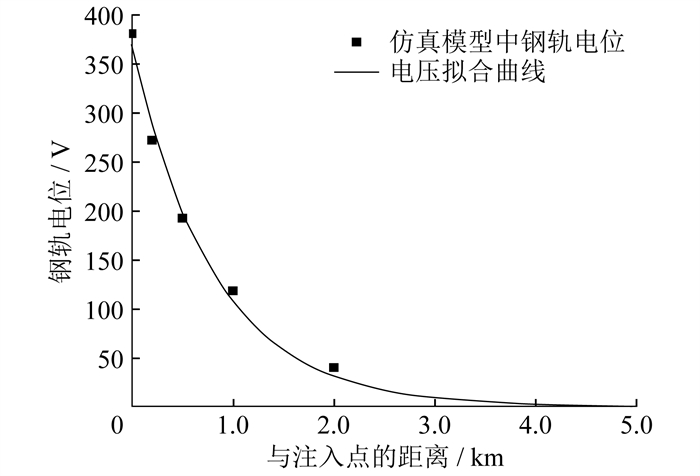
根据式(6),对表 1中数据用指数函数拟合出仿真模型中钢轨电位衰减趋势如图 7所示。
由图 7的电压拟合曲线可知,当电压行波传播到4.5 km时,钢轨电位已经不再下降,接近于零。由于在钢轨中间注入的电压左右各传播4.5 km,因此在钢轨模型的中间注入1.5/20 μs、幅值为380 V的冲击电压时,电压行波在钢轨上的传播距离 l为9 km。
基于以上分析,可计算出钢轨对排流网过渡电阻Rg为10.26 Ω·km。由于钢轨纵向电阻的影响,使冲击法计算得到的过渡电阻值比仿真模型中所设置的数值10 Ω·km略大。
3 实测案例
在仿真结果成立的基础上,对上海地铁某线路进行传统直流法和本文提出的新型冲击法的现场实测,对比两者实验数据,进一步验证在钢轨和排流网之间注入冲击电压测量其过渡电阻的可行性。冲击法现场实测接线如图 8所示。
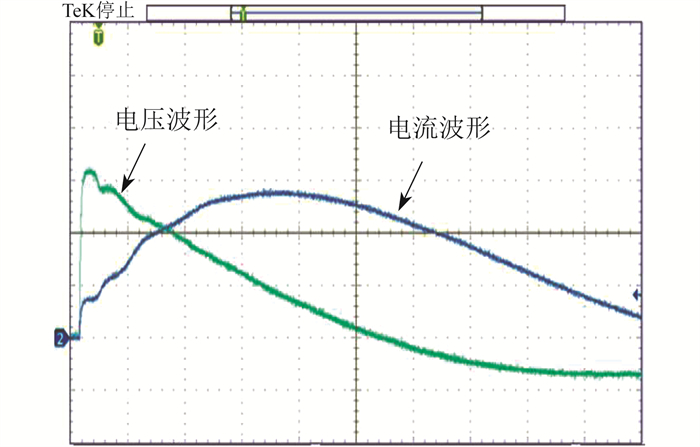
冲击电压源正负极分别与钢轨、排流网相连接,通过示波器测得并记录注入点现场实测冲击电压和冲击电流波形如图 9所示。示波器水平方向每大格所占扫描时间为10 μs。示波器垂直方向每大格所占电压幅值为100 V,电流幅值为20 A。
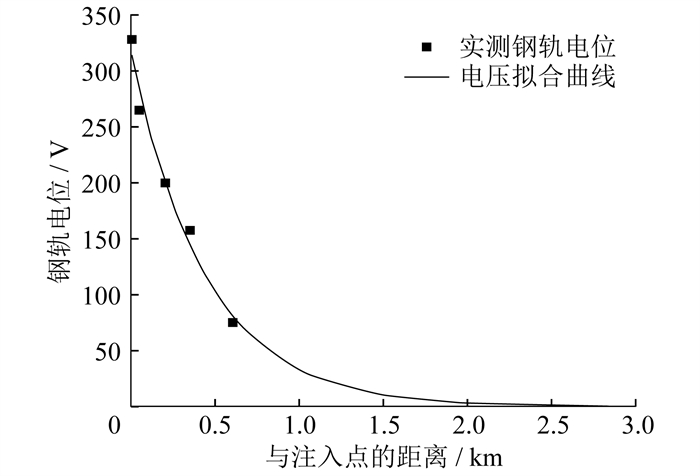
对冲击电压和冲击电流信号进行快速傅里叶变换,得到冲击电压直流分量U0为58.52 V,冲击电流直流分量I0为26.31 A,现场实测与注入点的距离对应的钢轨电位如表 2所示。
表 2
现场实测与注入点的距离对应的钢轨电位
| 与注入点的距离/m | 钢轨电位/V |
| 0 | 328 |
| 50 | 265 |
| 200 | 200 |
| 350 | 158 |
| 600 | 75 |
根据式(6),对现场实测钢轨电位数据用指数函数进行拟合,其衰减趋势如图 10所示。由图 10的电压拟合曲线可知,电压行波在单侧钢轨上的传播距离为2.5 km,因此电压行波在钢轨上的传播距离 l为5 km,使用冲击法计算出钢轨对排流网过渡电阻Rg为11.12 Ω·km。
通过直流法数据计算可得钢轨对排流网过渡电阻为10.72 Ω·km。由对比直流法和冲击法测量得到的过渡电阻可知,本文提出的新型冲击法相对于传统直流法测量误差为3.7%,但冲击法接线较直流法更加简便,抗干扰能力更强。
4 结论
本文首先介绍了轨道交通直流牵引系统和杂散电流形成机理,根据电压行波在钢轨中的传播规律以及快速傅里叶变换原理,提出了一种新型冲击法测量钢轨对排流网过渡电阻,最后通过仿真与实验对其进行验证,得到以下结论:
(1)在ATP-EMTP软件中搭建钢轨π型仿真模型,分析了钢轨模型分段长度的选择标准,在仿真中验证了可以用指数函数拟合钢轨电位的衰减规律,从而得到电压行波在钢轨上的传播距离。
(2)由仿真结果可知,冲击法计算得到的过渡电阻值比仿真模型中所设置的数值略大,主要是由于钢轨纵向电阻的影响,但单位长度钢轨纵向电阻仅为0.04 Ω/km,因此可忽略纵向电阻对冲击法测量过渡电阻的影响。
(3)通过对上海地铁某线路进行传统直流法和新型冲击法实测,对比两者实验数据,结果表明,两者误差为3.7%,验证了冲击法测量过渡电阻的可行性,且冲击法较直流法更加简便,抗干扰能力更强。
参考文献
-
[1]林炎华. 地铁牵引供电回路动态杂散电流研究[D]. 北京: 北京交通大学, 2019.
-
[2]朱峰, 李嘉成, 曾海波, 等. 城市轨道交通轨地过渡电阻对杂散电流分布特性的影响[J]. 高电压技术, 2018, 44(8): 2738-2745.
-
[3]CHARALAMBOUS C A. Comprehensive modeling to allow informed calculation of DC traction systems'stray current levels[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 9667-9677. DOI:10.1109/TVT.2017.2748988
-
[4]蔡力, 王建国, 樊亚东, 等. 地铁走行轨对地过渡电阻杂散电流分布的影响[J]. 高电压技术, 2015, 41(11): 3604-3610.
-
[5]LEE C H, LU C J. Assessment of grounding schemes on rail potential and stray currents in a DC transit system[J]. IEEE Transactions on Power Delivery, 2006, 21(4): 1941-1947. DOI:10.1109/TPWRD.2006.874561
-
[6]卢昱瑾. 地铁轨地过渡电阻测试技术研究[D]. 徐州: 中国矿业大学, 2021.
-
[7]胡传, 毕林. 地铁轨道系统电阻对杂散电流的影响分析[J]. 现代城市轨道交通, 2018(10): 47-52.
-
[8]国家市场监督管理总局, 中国国家标准化管理委员会. 轨道交通地面装置电气安全、接地和回流第2部分: 直流牵引供电系统杂散电流的防护措施: GB/T 28026. 2-2018[S]. 北京: 中国标准出版社, 2018: 18.
-
[9]孟昭亮, 董志伟, 杨媛, 等. 基于分布式传感器的地铁过渡电阻测量方法[J]. 传感器与微系统, 2022, 41(2): 128-131.
-
[10]王梓丞. 轨道电路传输模型与故障诊断方法研究[D]. 成都: 西南交通大学, 2019.
-
[11]赵智大. 高电压技术[M]. 3版. 北京: 中国电力出版社, 2006: 139-140.
-
[12]於玺. 快速傅里叶变换在信号处理中的应用[J]. 信息记录材料, 2021, 22(10): 184-186.
-
[13]中华人民共和国住房和城乡建设部. 地铁杂散电流腐蚀防护技术标准: CJJ/T 49-2020[S]. 北京: 中国建筑工业出版社, 2020: 42.
-
[14]陈邵东, 王孝波, 李斌. 标准雷电波形的频谱分析及其应用[J]. 气象, 2006, 32(10): 11-19.