|
|
|
发布时间: 2024-04-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-08-29
基金项目: 国家自然科学基金青年科学基金(51906133)
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2024)02-0169-09
|
摘要
针对可再生能源日渐高比例接入大电网,需要建立主动配电网系统来跟踪和响应大电网的调度需求,提出了一种基于联络线计划功率将微电网转变为主动配电网的经济性调度策略。该策略以风光储直流微电网并网运行系统成本最低为目标,运用改进麻雀搜索算法求解系统运行成本。与无联络线计划功率调度策略的调度结果进行了对比,结果表明,所提调度策略在满足大电网削峰填谷指令的同时,将系统的并网运行成本降低了9.79%。由此验证了该调度策略对于直流微电网并网经济性调度具有可行性。
关键词
直流微电网; 联络线计划功率; 调度策略; 削峰填谷; 麻雀搜索算法
Abstract
With the increasing integration of renewable energy sources into the main grid, the establishment of active distribution network systems is imperative to monitor and respond to the scheduling demands of the main grid. This paper presents a cost-effective scheduling strategy to transform microgrids into active distribution networks using interconnection power scheduling. The strategy aims to minimize the operational system costs of wind-solar-storage DC microgrids during grid-connected operation. An improved sparrow search algorithm is employed to solve the operational cost optimization. By comparing with the scheduling result of the non-interconnection power scheduling strategy, the proposed scheduling strategy reduces the grid-connected operational costs by 9.79%, while simultaneously fulfilling the peak-shaving and valley-filling directives from the main grid. These results verify the feasibility of the proposed scheduling strategy for economically dispatching grid-connected DC microgrids.
Key words
DC microgrid; planned power of the interconnection line; scheduling strategy; peak shaving and valley filling; sparrow search algorithm
微电网作为一种新型电力系统,可以利用可再生能源进行有序发电[1],然而可再生能源的大规模并网对电力系统的稳定性和经济性产生了不同程度的影响。随着太阳能、风能在大电网中所占比重越来越大,将大电网中分布式新能源高比例接入的节点作为一个主动配电网,在联网运行下服从大电网削峰填谷要求的经济性调度已经成为发展趋势[2-3]。目前,大电网中考虑更多的还是各个节点自身的经济性调度,但这种调度方案不利于大量分布式新能源在大电网中的接入。因此,将与大电网并网运行的微电网系统作为一个主动配电网[4],对大电网的指令通过联络线交换功率进行预设和跟踪,以保证整个电网的稳定运行。
在直流微电网并网系统中,联络线扮演着关键角色,通过实现微电源与大电网之间的协调和交互,为经济性调度提供了重要支持[5-7]。文献[8]将区域综合能源系统作为对象,以经济性和环保性为目标,建立混合整数线性规划模型,对比多种策略对具体问题进行优化调度。文献[9]运用多目标粒子群算法求解包含源‒储‒荷互动的分布式优化博弈模型,验证了该方法能够兼顾微电网个体的经济性、环保性以及满意度。文献[10]以社区综合能源系统为研究对象,将环境和运行总成本最低定为目标,进行日前优化调度并求解各设备最优出力。文献[11]运用微电网需求响应系统原理,分别构建了需求响应分时电价和实时电价优化策略,改进配电网总体负荷曲线并提升了微电网能源消纳比。
在以上研究中,均未以联络线交换功率作为切入点对系统作规划调度,而基于联络线计划功率进行优化调度可以求解各微电源最优出力并协调出力,有效降低系统的运行费用。智能优化算法由于其复杂的多目标非线性特性[12-13],被广泛运用于微电网优化调度寻找最优解。当前,许多学者对智能优化算法进行了大量的探索和改进,将其应用于不同的场景中。文献[14]采用改进鸡群算法和粒子群算法对典型微电网系统进行调度优化。文献[15]结合微电网经济性和分布式电源在不同时间段内的波动性等因素,运用改进粒子群算法对微电网优化调度进行求解。文献[16]在微电网并网运行模式下提出了一种双层优化调度方法,采用改进粒子群算法对其建立的微电网并网系统进行实时能量管理。文献[17]以系统安全运行作为约束,利用标准蜂群算法对系统的运行成本进行寻优,有效降低了运行成本。文献[18]将多目标问题转换为单目标问题,使用改进遗传算法对并网系统进行调度寻优。文献[19]建立了风光柴储微电网系统,提出了混合策略的改进麻雀搜索算法(Sparrow Search Algorithm,SSA),有效降低了微电网的运行成本。但是,群体智能优化算法普遍存在种群多样性不足、迭代后期容易陷于局部最优等缺点。SSA是一种新兴的群体智能优化算法[20],其利用麻雀的搜索能力和抗捕食能力进行迭代优化,具有调整参数少、收敛快、计算简单等优点。本文将SSA应用于风光储直流微电网优化调度,利用Tent混沌映射丰富初始化种群,扩大了搜索范围,为提高算法的全局搜索能力进而避免在算法寻优后期陷入局部最优解,引入了线性递减的权重优化策略对SSA进行改进。
为了验证联络线计划功率在满足大电网发电削峰填谷需求的同时在经济性调度上可明显降低运行成本,本文建立了风光储直流微电网并网运行系统,并以运行成本最低为目标建立经济优化模型,提出了一种基于联络线计划功率的调度策略。通过对满足大电网削峰填谷需求的联络线功率指令进行跟踪,运用改进SSA求解风光储系统各个时刻的最优输出功率,并且对比有无联络线计划功率经济性调度的运行成本,验证本文所提调度策略的有效性和可行性。
1 含分布式电源的直流微电网发电模型构建
微电网优化运行的目标是通过合理调配微电源的输出功率以实现各微电源和负荷需求之间的平衡,从而达到更加经济性运行的目的。为实现此目标,需要对直流微电网并网运行系统模型以及各分布式电源数学模型进行准确构建,以便对微电源和储能单元进行合理地优化调度。
1.1 系统结构
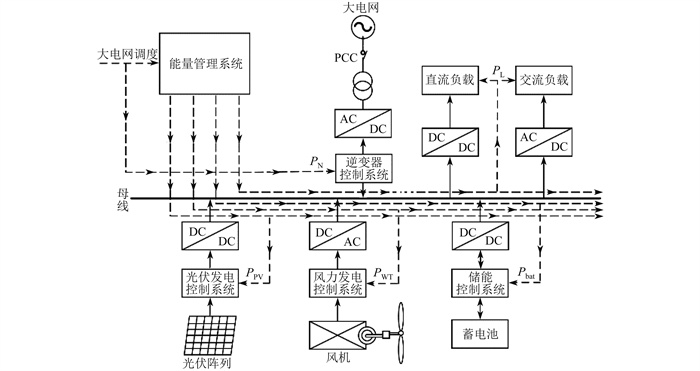
本文建立的风光储直流微电网并网运行系统主要包含风力发电系统、光伏发电系统、储能系统以及负荷,其整体结构如图 1所示。风机和光伏系统输出功率取决于两种负荷共同作用的大小,储能系统作为辅助发电装置,在确保系统稳定运行方面发挥了至关重要的作用。
图 1中,AC和DC分别表示交流和直流,直流微电网作为独立的网络通过公共连接点(Point of Common Coupling,PCC)和大电网进行连接,实现并网运行,并接受大电网对联络线功率的调度。大电网为联络线功率PN制定发电计划,风机输出功率PWT、光伏系统输出功率PPV和蓄电池充放电功率Pbat跟踪联络线计划功率,在实现系统内部稳定运行即满足负荷所需用电量PL的同时,有效降低了系统整体的运行成本,提高了可靠性。
1.2 分布式电源数学模型
1.2.1 光伏发电模型
光伏系统输出功率主要受光照强度和温度的影响,表示为
| $ P_{\text {PV }}=P_{\mathrm{STC}} \frac{G}{G_{\text {STC }}}\left\{1+k\left[T_{\mathrm{o}}-T_{\mathrm{STC}}\right]\right\} $ | (1) |
式中:PSTC——标准测试条件下的发电输出功率;
G——实际光照强度;
GSTC——标准测试条件下的光照强度;
k——功率温度系数;
TO——光伏电池组表面温度;
TSTC——标准测试条件下的环境温度。
1.2.2 风力发电模型
风机输出功率为
| $ P_{\mathrm{WT}}= \begin{cases}0, & \text { 其他 } \\ P_{\mathrm{r}} \frac{\left(v-v_{\mathrm{ci}}\right)}{\left(v_{\mathrm{r}}-v_{\mathrm{ci}}\right)}, & v_{\mathrm{ci}}<v \leqslant v_{\mathrm{r}} \\ P_{\mathrm{r}}, & v_{\mathrm{r}}<v \leqslant v_{\mathrm{co}}\end{cases} $ | (2) |
式中:Pr——风机的额定输出功率;
v,vr——风机的实际风速、额定风速;
vci,vco——风机的切入、切出风速。
1.2.3 储能模型
直流微电网的储能装置为蓄电池,其剩余容量计算公式以及荷电状态(State of Charge,SOC)的表达式分别为
| $ W_{\mathrm{BSS}}^t=W_{\mathrm{BSS}}^{t-1}\left(1-\tau_{\mathrm{BSS}}\right)+\eta_{\mathrm{ch}} P_{\mathrm{ch}}^t \Delta t-\frac{P_{\text {disch }}^t}{\eta_{\text {disch }} \Delta t} $ | (3) |
| $ S_{\mathrm{OC}}^t=S_{\mathrm{OC}}^{t-1}\left(1-\tau_{\mathrm{BSS}}\right)+\frac{\eta_{\mathrm{ch}} P_{\mathrm{ch}}^t \Delta t-P_{\text {disch }}^t /\left(\eta_{\text {disch }} \Delta t\right)}{W_{\mathrm{BSS}}} $ | (4) |
式中:WBSSt,WBSSt-1——t和t-1时段内蓄电池自身的剩余容量;
τBSS——t时段内蓄电池自放电率;
ηch,ηdisch——蓄电池自身的充电、放电效率;
Pcht,Pdischt——t时段内蓄电池自身的充电、放电功率;
SOCt,SOCt-1——t时段和t-1时段内蓄电池SOC;
WBSS——蓄电池自身额定容量。
2 经济优化模型构建
本文所建立的风光储直流微电网并网运行系统,在满足约束条件的基础上,协调风光储系统的输出功率进而对整体系统进行寻优调度。因此,建立的经济优化模型在考虑联络线计划功率的同时,调节各微电源输出功率,使得目标函数最优。
2.1 目标函数
以运行成本最低为目标,其目标函数为
| $ \min F=C_{\mathrm{pV}}+C_{\mathrm{wT}}+C_{\mathrm{bat}}+C_{\mathrm{N}} $ | (5) |
| $ \left\{\begin{array}{l} C_{\mathrm{PV}}=\sum\limits_{t=1}^T P_{\mathrm{PV}}(t) \cdot W_{\mathrm{PV}}(t) \\ C_{\mathrm{WT}}=\sum\limits_{t=1}^T P_{\mathrm{WT}}(t) \cdot W_{\mathrm{WT}}(t) \\ C_{\text {bat }}=\sum\limits_{t-1}^T P_{\text {bat }}(t) \cdot W_{\text {bat }}(t) \\ C_{\mathrm{N}}=\sum\limits_{t=1}^T P_{\mathrm{N}}(t) W_G(t) r(t)-P_{\mathrm{N}}(t) W_{\mathrm{M}}(t)[1-r(t)] \end{array}\right. $ | (6) |
式中:F——直流微电网并网运行系统日运行成本;
CPV,CWT,Cbat,CN——光伏发电系统、风力发电系统、储能系统、大电网运行成本;
T——系统运行一日分成的时段总数;
PPV(t),PWT(t)——t时段内光伏系统、风机输出功率;
WPV(t),WWT(t)——t时段内光伏发电系统、风力发电系统购电单位成本;
Pbat(t)——t时段内蓄电池充放电功率;
Wbat(t)——t时段内蓄电池从充电状态到放电状态的运行单位成本;
PN(t)——t时段内大电网联络线功率;
WG(t),WM(t)——t时段内微电网向大电网购电、售电单位成本;
r(t)——t时段内状态变量,当微电网向大电网售电时为0,购电时为1。
2.2 约束条件
2.2.1 功率平衡约束
| $ P_{\mathrm{L}}(t)=P_{\mathrm{PV}}(t)+P_{\mathrm{WT}}(t)+P_{\text {bat }}(t)+P_{\mathrm{N}}(t) $ | (7) |
式中:PL(t)——t时段内直流微电网并网运行系统的总负荷。
2.2.2 功率不等式约束
光伏系统和风机运行约束条件:
| $ P_{\mathrm{PV}, \min } \leqslant P_{\mathrm{PV}}(t) \leqslant P_{\mathrm{PV}, \max } $ | (8) |
| $ P_{\mathrm{WT}, \min } \leqslant P_{\mathrm{WT}}(t) \leqslant P_{\mathrm{WT}, \max } $ | (9) |
式中:PPV,min,PPV,max——光伏系统输出功率的下限和上限;
PWT,min,PWT,max——风机输出功率下限和上限。
储能系统运行约束条件:
| $ S_{\mathrm{OC}, \min } \leqslant S_{\mathrm{OC}}^t \leqslant S_{\mathrm{OC}, \max } $ | (10) |
| $ P_{\text {ch.} \max } \leqslant P_{\text {bat }}(t) \leqslant P_{\text {disch.} \text { max }} $ | (11) |
式中:SOC,min,SOC,max——蓄电池SOC的最小值和最大值;
Pch.max,Pdisch.max——蓄电池的最大充、放电功率。
微电网与大电网功率交换约束条件:
| $ P_{\mathrm{N}, \min } \leqslant P_{\mathrm{N}}(t) \leqslant P_{\mathrm{N}, \text { max }} $ | (12) |
式中:PN,min,PN,max——微电网与配电网功率交换最小值和最大值。
3 基于改进SSA的调度
3.1 SSA
SSA通过模拟麻雀觅食和避免捕食者的行为,寻找最优解和最优路径。SSA个体分为发现者、跟随者与侦察者。发现者主要为种群提供觅食方向,跟随者跟随发现者觅食,侦察者对觅食区域进行监视。侦察者占个体总数的10%~20%,发现者与跟随者是动态变化的。通过不断更新三者位置,完成食物获取。
首先,初始化种群位置[21]。种群的初始位置 P可以用一个矩阵表示,总共有m只麻雀,即种群个数为m,矩阵的每一行表示在d维空间内每只麻雀初始的位置:
| $ \boldsymbol{P}=\left[\begin{array}{ccc} P_{1,1} & \cdots & P_{1, d} \\ \vdots & \vdots \\ P_{m, 1} & \cdots & P_{m, d} \end{array}\right] $ | (13) |
在d维空间内,所有麻雀的初始适应度值F为
| $ \boldsymbol{F}=\left[\begin{array}{c} f\left(\left[P_{1,1} \cdots P_{1, d}\right]\right) \\ \vdots \\ f\left(\left[P_{m, 1} \cdots P_{m, d}\right]\right) \end{array}\right] $ | (14) |
其中,f(·)表示个体的适应度值。
在种群中将适应度值高的麻雀作为发现者,且发现者通过不断地移动来寻找更多的食物,而其他跟随者也随之移动位置。通过报警值与安全值比较使发现者根据不同方式更新位置。发现者位置更新公式为
| $ \boldsymbol{P}_{i, j}^{l+1}= \begin{cases}\boldsymbol{P}_{i, j}^l \cdot \exp \left(\frac{-i}{\alpha l_{\max }}\right), & R<S_{\mathrm{T}} \\ \boldsymbol{P}_{i, j}^l+Q \cdot \boldsymbol{L}, & R \geqslant S_{\mathrm{T}}\end{cases} $ | (15) |
式中:Pi,jl——迭代第l次时种群中第i个体的第j维位置;
α——(0,1]中的均匀随机数;
lmax——迭代的最大次数;
R——侦察麻雀发现捕食者发出鸣叫的报警值,取[0 1]中的均匀随机数;
ST——预设的安全值,取值范围为[0.5,1];
Q——标准正态分布随机数;
L——值都为1的1 x d维的矩阵。
在种群中选取70%~80%作为发现者,其余均为跟随者,跟随者位置更新公式为
| $ \boldsymbol{P}_{i, j}^{l+1}= \begin{cases}Q \cdot \exp \left(\frac{\boldsymbol{P}_{\text {worst }}^l-\boldsymbol{P}_{i, j}^l}{i^2}\right), & i>\frac{m}{2} \\ \boldsymbol{P}_{\mathrm{g}}^{l+1}+\left|\boldsymbol{P}_{i, j}^l-\boldsymbol{P}_{i, j}^{l+1}\right| \cdot \boldsymbol{A}^{+} \cdot \boldsymbol{L}, & i \leqslant \frac{m}{2}\end{cases} $ | (16) |
式中:Pworstl——迭代第l次时当前种群中麻雀的全局最差位置;
Pgl+1——迭代第l+1次时种群中最优个体的位置;
A+——d x 1维的矩阵,A+ = AT (AAT)-1,A为1×d矩阵,其中每个元素随机赋值为1或−1。
根据式(16),当i > m ∕ 2时,第i个跟随者适应度值低,不能与发现者竞争;当i ≤ m ∕ 2时,跟随者在最优个体附近觅食。
种群中随机选取10%~20%的麻雀作为侦察者负责警戒,如有危险则立即移动到下一个位置。侦察者位置更新公式为
| $ \boldsymbol{P}_{i, j}^{l+1}= \begin{cases}\boldsymbol{P}_{\text {best }}^l+\beta \cdot\left|\boldsymbol{P}_{i, j}^l-\boldsymbol{P}_{\text {best }}^l\right|, & F_i \neq F_{\mathrm{g}} \\ \boldsymbol{P}_{i, j}^l+K \cdot\left[\frac{\left|\boldsymbol{P}_{i, j}^l-\boldsymbol{P}_{\text {worst }}^l\right|}{\left(F_i-F_{\mathrm{w}}\right)+\varepsilon}\right], & F_i=F_{\mathrm{g}}\end{cases} $ | (17) |
式中:Pbestl——当前种群中麻雀的全局最优位置;
β——满足正态分布的随机数;
Fi——当前个体i的适应度值;
Fg,Fw——当前全局最优、最差位置对应的适应度值;
K——[-1, 1]中的均匀随机数;
ε——最小常数。
根据式(17),若当前侦查者个体适应度值不为全局最优,需更换到适应度更高的位置;若当前侦察者位置就是最佳位置时,将接近同伴。
3.2 改进SSA
3.2.1 混沌搜索策略
混沌映射常应用于寻优问题中,其中Tent模型和Logistic模型是最常用的混沌模型,而Tent混沌映射的遍历均匀性和收敛速度均优于Logistic映射。为了增加SSA初始种群多样性,本文采用Tent混沌映射对麻雀种群进行初始化,使种群分布均匀,增加随机变量rand(0,1)x(1 ∕ N),此处N取10,优化后的函数表达式为[22]
| $ x_{n+1}= \begin{cases}2\left[x_n+0.1 \cdot \operatorname{rand}(0,1)\right], & 0 \leqslant x_n \leqslant 0.5 \\ 2\left[1-x_n+0.1 \cdot \operatorname{rand}(0,1)\right], & 0.5<x_n \leqslant 1\end{cases} $ | (18) |
式中:xn,xn+1——Tent混沌映射迭代前后的值,xn+1∈[0, 1]。
在使用Tent混沌映射来初始化麻雀算法的种群时,是通过生成一系列标量值来间接构建每个麻雀在其各个维度上的位置。这个过程通常涉及对每个维度分别使用Tent混沌映射,从而为每个麻雀生成一个完整的位置向量。具体过程如下。
(1)选择初始值 对于某个维度,选择一个初始值x0,这些初始值可以是随机的,也可以是预先设定的。
(2)应用Tent混沌映射 对于每个维度,可以多次独立地应用Tent混沌映射,每次迭代后产生的数值将作为下一次迭代前的数值。
(3)生成向量 重复上述步骤,直到该维度生成足够数量的元素,再将这些元素组合起来,形成一个完整的向量。
(4)重复构建种群 重复上述整个过程,直到为算法的初始种群构建了足够数量的向量。
3.2.2 基于线性递减的权重优化策略
本文提出线性递减权重策略,将惯性权重按照线性由大到小依次递减,提升了算法的收敛速度,优化了算法在寻优后期容易陷入局部最优的问题,其公式为
| $ w=w_{\max }-\frac{r\left(w_{\max }-w_{\min }\right)}{r_{\max }} $ | (19) |
式中:w——惯性权重;
wmax,wmin——惯性权重的最大值和最小值;
r,rmax——当前和最大迭代步数。
改进后的SSA中发现者位置公式更改为
| $ \boldsymbol{P}_{\mathrm{D}_{i j}}^{l+1}= \begin{cases}\boldsymbol{P}_{i, j}^l+w \cdot \delta\left|\boldsymbol{P}_{i, j}^l-\boldsymbol{F}_{\mathrm{g}}^l\right|, & R<S_{\mathrm{T}} \\ \boldsymbol{P}_{i, j}^l+Q \cdot \boldsymbol{L}, & R \geqslant S_{\mathrm{T}}\end{cases} $ | (20) |
式中:
δ——随机数,δ ∈[0 1];
Fgl——迭代第l次时种群全局最优适应度。
3.2.3 改进SSA的算法流程
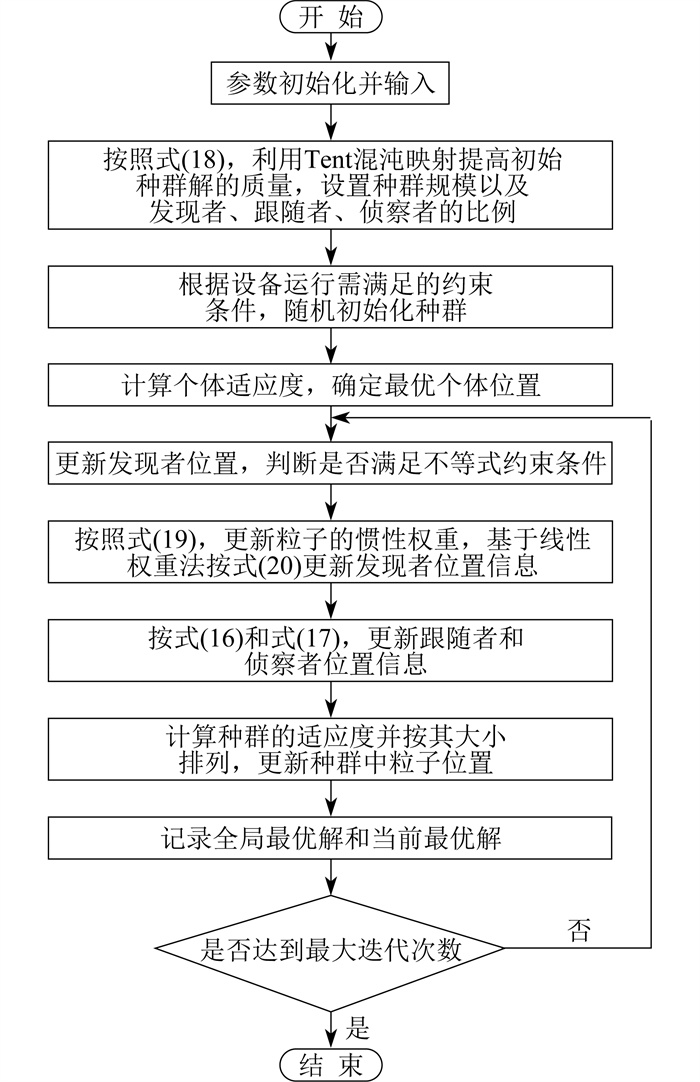
结合以上改进策略,应用于直流微电网并网运行系统优化调度的改进SSA的算法流程如图 2所示。
4 案例分析
本文构建了如图 1所示的风光储直流微电网并网运行系统模型。优化周期定为24 h,并根据日内调度的要求均分为96个时段,每个时段15 min,各个时段对应不同的购电价格和售电价格。根据大电网负荷功率发电计划,制定联络线功率计划曲线,利用大电网计划功率削峰填谷,提升大电网与微电网之间的供需平衡。在满足约束条件的基础上,利用改进SSA求解微电网优化运行模型,对有无联络线功率发电计划的两种调度情况进行对比,确定每种微电源的输出功率情况,实现微电网运行成本最低。
4.1 设备参数设置
本文所建立的风光储直流微电网并网运行系统各分布式电源参数设置如表 1所示。各个时段负荷所需用电量如表 2所示。各个时段售购电价如表 3所示。利用改进SSA进行模型求解,设置发现者、跟随者、侦察者的比例分别为70%、20%、10%。
表 1
各分布式电源参数
| 系统 | 额定功率/kW | 维护系数/(元/kWh) |
| 光伏发电系统 | 280 | 0.54 |
| 风力发电系统 | 380 | 0.69 |
| 储能系统 | 300 | 0.30 |
表 2
各个时段负荷所需用电量
| 时段序号 | 负荷所需用电量/kW |
| 1 | 88.24 |
| 2 | 86.93 |
| 3 | 85.63 |
| ︙ | ︙ |
| 94 | 99.69 |
| 95 | 107.46 |
| 96 | 115.46 |
表 3
各个时段售购电价
| 时段序号 | 售电价格 | 购电价格 |
| 1~28 | 0.23 | 0.31 |
| 29~40 | 0.33 | 0.83 |
| 41~60 | 0.52 | 1.08 |
| 61~72 | 0.33 | 1.08 |
| 73~84 | 0.52 | 0.83 |
| 85~96 | 0.33 | 0.68 |
4.2 仿真结果分析
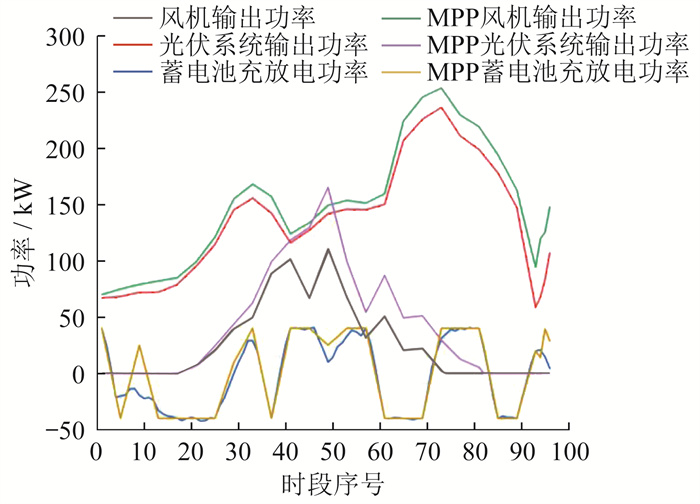
本文以该电网某一日的数据作为算例输入量。当联络线功率有计划时,通过优化调度确定风光储系统的最优输出功率,而当联络线功率无计划时,按当前时刻的最大功率点(Maximum Power Point,MPP)发电。风光储系统的输出功率曲线对比如图 3所示。
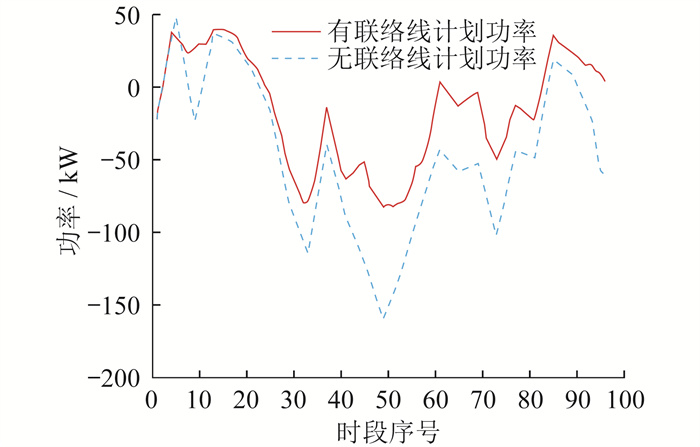
有无联络线计划功率曲线对比如图 4所示。
由图 4可知,当处于低负荷时,联络线功率大于零,大电网向微电网注入电能,在确保微电网正常运行的同时,将多余的电能储存起来以备高负荷时使用,同时对微电网和大电网实现了填谷功能;当处于高负荷时,联络线功率小于零,即联络线将微电网多余的发电能力纳入大电网,以减轻大电网的负荷压力,达到削峰效果。
有无联络线计划功率的优化调度结果对比如图 5所示。
由图 5(a)可知:在0:00—7:00期间,由于负荷较低且风机持续出力,根据联络线功率计划,只需为微电网提供少量电量,蓄电池在此过程中不断充放电维持系统平衡;在8:00—10:00期间,光伏系统、风机同时出力,蓄电池在此过程中配合供需进行充放电;在10:00—13:00期间,此时处于用电高峰期,大电网售电价格最高,在充分利用光伏系统和风机发电达到负荷所需用电量后将多余电量卖给大电网,获取收益;在13:00—15:00期间,由于负荷所需用电量下降,蓄电池进行充电;17:00— 20:00时段是一日中所需微电源出力最大时段,而19:00—21:00也是另一个电网售价最高的时段,在保证微电网运行稳定的同时,尽量多地向大电网销售电量,以获取最高的收益;在21:00—24:00期间,电价相对较低,在风机和蓄电池出力的同时向大电网购电,维持负荷所需用电量。
由图 5(b)可知,无联络线计划功率调度时光伏系统和风机一直处于MPP输出状态,其运行成本明显升高,而通过联络线将微电网所发多余电量卖给大电网所获收益明显小于光伏系统和风机的运行成本,在没有满足大电网削峰填谷发电的情况下,其整体调度费用明显提高。
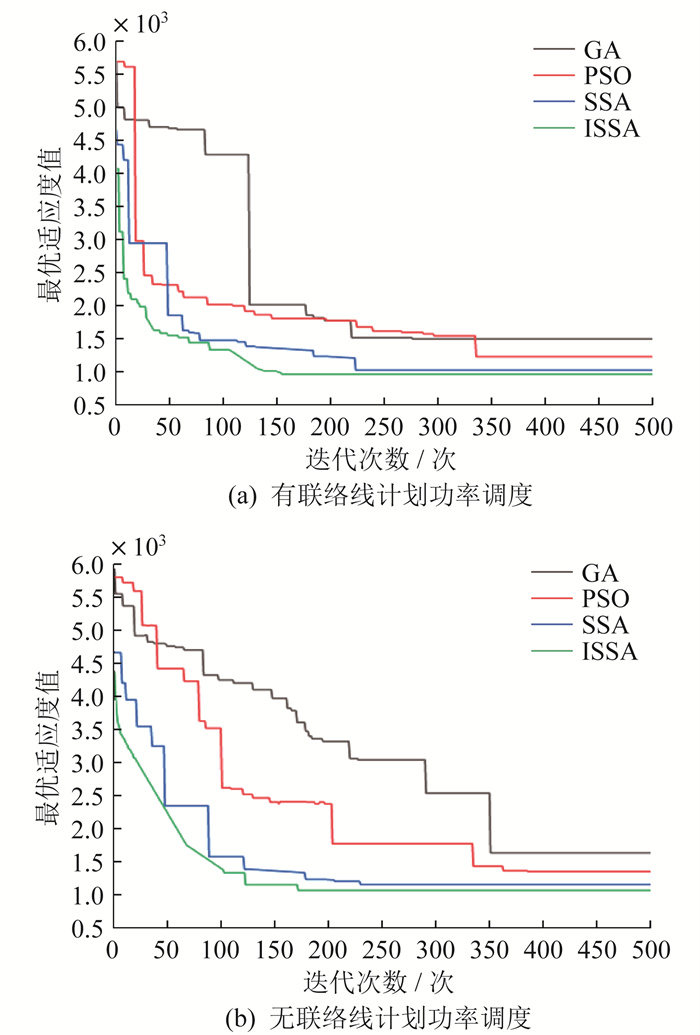
为了证明本文所提出的有联络线计划功率调度策略相较于无联络线计划功率调度策略在运行成本上有明显降低,同时验证改进SSA具有更好的寻优能力,将ISSA(改进SSA)、原始SSA、粒子群优化(Particle Swarm Optimization,PSO)算法、遗传算法(Genetic Algorithm,GA)在两种调度方式的迭代过程与结果进行对比,迭代次数设定为500次,个体数设定为100。各优化算法迭代曲线对比如图 6所示。
各优化算法调度结果如表 4所示。
表 4
各优化算法调度结果
| 调度方式 | 优化算法 | 迭代次数/次 | 运行成本元 |
| 有联络线计划功率 | GA | 277 | 1 491.85 |
| PSO | 336 | 1 229.00 | |
| SSA | 224 | 1 021.44 | |
| ISSA | 154 | 962.75 | |
| 无联络线计划功率 | GA | 351 | 1 631.85 |
| PSO | 386 | 1 349.00 | |
| SSA | 230 | 1 153.44 | |
| ISSA | 172 | 1 067.25 |
由图 6可知,ISSA在迭代初期的收敛速度明显提升并且迭代次数最少,更好的全局搜索能力也使得其结果更优,即运用ISSA进行日内调度的运行成本最低,综合性能最优。
由表 4可知:在运用ISSA对系统采用无联络线计划功率进行优化调度时,仅迭代172次后便达到了全局最优,而对系统采用有联络线计划功率进行优化调度时,仅迭代154次后便达到了全局最优,两种调度方式下,ISSA的迭代次数均低于GA、PSO和SSA;无联络线计划功率调度与有联络线计划功率调度在同样运用ISSA进行求解时,其日运行成本分别为1 067.25元、962.75元。相较于SSA,运用ISSA后调度在成本上降低了104.50元,优化幅度为9.79%。综上所述,运用有联络线计划功率调度策略的直流微电网运行时,各微电源的输出功率更合理,在对大电网输出功率起到削峰填谷作用的同时,也使得其自身运行成本更低。
5 结语
为了使直流微电网并网运行系统通过联络线功率在满足大电网削峰填谷需求的同时降低运行成本,本文提出了一种基于联络线计划功率的优化调度策略,将以上策略应用到风光储直流微电网并网运行系统中,运用多种优化算法对风光储系统最优输出功率进行求解。相比于原始SSA,ISSA跳出局部最优的能力更强,寻优得到的运行成本更低,并且在满足负荷所需用电量的基础上,对联络线计划功率进行跟踪,其调度结果表明,直流微电网作为主动配电网,对大电网发电进行削峰填谷具有可行性。
参考文献
-
[1]曾君, 徐冬冬, 刘俊峰, 等. 考虑负荷满意度的微电网运行多目标优化方法研究[J]. 中国电机工程学报, 2016, 36(12): 3325-3334.
-
[2]王成山, 李鹏. 分布式发电微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-14.
-
[3]马艺玮, 杨苹, 王月武, 等. 微电网典型特征及关键技术[J]. 电力系统自动化, 2015, 39(8): 168-175.
-
[4]ZHAO K, ZHANG B, ZHAO G F, et al. Comprehensive dispatching optimization for distribution network containing microgrid[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing, China: IEEE, 2018: 8582665.
-
[5]李博文, 靳斌, 刘玉芬. 微电网经济调度研究综述[J]. 科技创新与应用, 2016(23): 216.
-
[6]郗宏伟. 微电网运行策略及优化方法研究[D]. 秦皇岛: 燕山大学, 2013.
-
[7]BAI D, ZHANG T Y, YANG Z, et al. Research on grid-connected micro grid control strategy and control method[C]//2017 IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing, China: IEEE, 2017: 8245459.
-
[8]李良余, 马守达, 盛晏. 基于经济性和环保性的区域综合能源系统优化调度研究[J]. 上海电力学院学报, 2019, 35(5): 503-509.
-
[9]王侨侨, 曾君, 刘俊峰, 等. 面向微电网源-储-荷互动的分布式多目标优化算法研究[J]. 中国电机工程学报, 2020, 40(5): 1421-1432.
-
[10]刘蓉晖, 马天天, 高远, 等. 考虑需求侧协同响应的社区综合能源系统低碳经济调度[J]. 上海电力大学学报, 2020, 36(5): 421-430.
-
[11]陈冉, 杨超, 沈冰, 等. 基于微电网的需求响应优化策略[J]. 电力系统保护与控制, 2018, 46(11): 124-130.
-
[12]黄杨, 胡伟, 闵勇, 等. 考虑日前计划的风储联合系统多目标协调调度[J]. 中国电机工程学报, 2014, 34(28): 4743-4751.
-
[13]雷庆军. 考虑环境效益的微电网双层经济调度[D]. 长沙: 湖南大学, 2017.
-
[14]李静雅, 易庚, 胡汉梅, 等. 基于改进鸡群算法的微电网协同优化运行研究[J]. 高压电器, 2019, 55(7): 203-210.
-
[15]于新海, 王鑫, 苏日古格, 等. 基于GA和IPSO的微电网调度优化与对比分析[J]. 电气传动, 2022, 52(22): 38-43.
-
[16]许晓慧, 苏义荣, 施勇, 等. 并网运行模式下微电网能量优化调度算法研究[J]. 电网与清洁能源, 2016, 32(8): 117-122.
-
[17]薛贵挺, 张健. 基于人工蜂群算法的微电网环保经济调度[J]. 电工电气, 2016(10): 57-60.
-
[18]陈洁, 杨秀, 朱兰, 等. 微网多目标经济调度优化[J]. 中国电机工程学报, 2013, 33(19): 57-66.
-
[19]王汉宇. 基于改进麻雀搜索算法的微电网优化调度[J]. 兰州文理学院学报(自然科学版), 2022, 36(6): 59-63.
-
[20]XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
-
[21]薛涛, 张安杰. 多策略改进的麻雀搜索算法及应用[J]. 西安工程大学学报, 2023, 37(2): 96-104.
-
[22]SHAN L, QIANG H, LI J, et al. Chaotic optimization algorithm based on Tent map[J]. Control and Decision, 2005, 20(2): 179-182.