|
|
|
发布时间: 2024-06-28 |
综合能源 |
|
|
|
收稿日期: 2023-12-29
基金项目: 国家自然科学基金(51977030)
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2024)03-0227-08
|
摘要
考虑到系统运行经济性的影响,对基于需求侧响应(DR)的风力发电与先进绝热压缩空气储能(AA-CAES)系统协调优化问题进行了研究。首先,基于分时电价构建了用户多时段需求侧响应模型,并根据AA-CAES系统的压缩、膨胀功率建模。其次,以系统的固定成本、设备维护成本、购电成本、售电成本以及调峰成本共同构成系统总成本,采用动态规划法对AA-CAES系统的压缩、膨胀功率进行优化,求得系统总成本最小的风力发电与AA-CAES系统最优容量配置。最后,通过仿真验证所提优化方法的可行性。
关键词
先进绝热压缩空气储能; 分时电价; 动态规划法; 容量优化配置; 需求侧响应
Abstract
Considering the impact of system operation economics, the problem of coordinated optimization of wind power generated and advanced adiabatic compressed air energy storage(AA-CAES) systems based on demand response is analyzed. Firstly, the time-of-use power price model of user's multi-time period is constructed based on the demand response; the compression and expansion power is modeled for AA-CAES. Secondly, the fixed cost, equipment maintenance cost, power purchase cost and sale cost, and peaking cost together constitute the total cost of the system, and the compression/expansion power of AA-CAES is optimized by dynamic programming method to find the optimal wind allocation capacity of wind power generated and AA-CAES systems with the minimum total cost. Finally, the feasibility of the proposed optimization method is verified by simulation.
Key words
advanced adiabatic compressed air energy storage; time-of-use power price; dynamic programming method; capacity optimized allocation; demand response
“双碳”战略目标的提出对以可再生能源为核心的电力系统快速推进具有重要意义[1]。由于可再生能源出力的不确定性和随机性[2],以及负荷的不确定性[3],使其消纳受到影响,导致电力系统供需平衡的难度提高。因此,传统电力系统模型已无法满足当下高占比新能源的电力系统对稳定灵活运行的要求。其中,风能作为一种清洁的可再生能源在能源体系中占据了重要位置[4]。压缩空气储能是有效解决风电消纳问题的方法之一[5]。先进绝热压缩空气储能(Advanced Adiabatic Compressed Air Energy Storage,AA-CAES)不需要化石燃料,通过分级的压缩膨胀,较传统的压缩空气储能效率更高[6-7]。德国的Huntorf电站和美国的McIntosh电站已将该技术投入商业运行[8]。然而,我国AA-CAES技术尚处于工程示范阶段。2021年8月4日,我国首座并网的压缩空气储能商业电站——山东省泰安市肥城1万kW压缩空气储能电站一次送电成功[9]。
现阶段AA-CAES技术应用造价昂贵且价格随容量增加逐渐提高。为了提高经济性,同时也为了充分消纳风电,系统需要先引导用户改变其用电习惯。电力需求侧管理(Demand Side Management,DSM)是指企业或政府(供应侧)采取相关措施,鼓励电力用户(需求侧)改变原有的用电习惯,在保证能源服务水平的情况下,提高需求侧用电效率,实现最低能源成本服务所进行的管理活动[10]。需求侧响应(Demand Response,DR)属于短期的DSM,通常通过价格变化等措施来调整需求侧的用电习惯,分时电价是其中最直接也是最有效的一种方法,将一天不同时段的电价赋予不同价格,刺激用户将高峰时段的用电量转移到低谷时段[11-12]。文献[13]基于价格的DR建立了弹性负荷曲线。文献[14] 通过电量电价弹性系数描述分时电价的响应过程。文献[15] 提出了面向配电网光伏接纳能力提升的分时电价优化方法。文献[16]在考虑电价的情况下,提出了计及综合需求响应下含多类型微电网的配电网混合博弈优化调度方法,有效降低了配电网和微电网的运行成本,实现了更合理地调度可控资源。
综上,本文对基于DR的风力发电与AA-CAES系统协调优化问题进行了研究。在分时电价场景下,对负荷构建用户多时段DR模型,将其计入年运行费用,并构建系统的经济性模型,采用动态规划法求解AA-CAES系统的压缩、膨胀功率,得到风力发电与AA-CAES系统的最优容量,该研究对于配置AA-CAES系统改善风电的波动性以及调整电力负荷用户的用电习惯具有重要意义,可为日后AA-CAES技术大规模商业化运用提供理论基础。
1 用户多时段DR模型
考虑配置AA-CAES系统容量时无需太高的实时性,因此本文构建了基于峰、平、谷时段分时电价的用户多时段DR模型。
用户多时段DR是指实行分时电价后用户不仅调整自己当前时段的用电量,还将进一步影响其他时段的用电量,故负荷不但与当前时段的电价有关,而且其他时段的电价也对其有影响。根据电量电价之间的平衡关系和多时段电量电价弹性矩阵,可建立用户多时段DR模型[17]。由于电量与电价曲线很难用函数表达,因此在经济学上将其线性化,即通过电量变化率和电价变化率描述电量电价弹性系数m。其表达式为
| $ m=\frac{\Delta E}{E}\left(\frac{\Delta e}{e}\right)^{-1} $ | (1) |
式中:∆E——电量变化量;
E——电量;
∆e——电价变化量;
e——电价。
电量E与电价e近似成线性关系,即E=-ae+b,a和b均为电量-电价曲线参数。
基于峰、平、谷时段分时电价的电量电价弹性矩阵M的表达式为
| $ \boldsymbol{M}=\left[\begin{array}{lll} m_{\mathrm{ff}} & m_{\mathrm{fp}} & m_{\mathrm{fg}} \\ m_{\mathrm{pf}} & m_{\mathrm{pp}} & m_{\mathrm{pg}} \\ m_{\mathrm{gf}} & m_{\mathrm{gp}} & m_{\mathrm{gg}} \end{array}\right] $ | (2) |
矩阵M的对角线元素mxx(x=f,p,g)为自弹性系数,其余元素mxy(y=f,p,g)为交叉弹性系数,其表达式[18]为
| $ \left\{\begin{array}{l} m_{x x}=\frac{-a_x e_x}{-a_x e_x+b_x} \\ m_{x y}=\frac{a_y e_y}{-a_x e_x+b_y} \end{array}\right. $ | (3) |
式中:af,bf,ap,bp,ag,bg——峰、平、谷时段电量-电价曲线参数;
ef,ep,eg——峰、平、谷时段电价。
实行分时电价后电量ETOU表达式为
| $ \begin{aligned} \boldsymbol{E}_{\mathrm{TOU}} & =\boldsymbol{E}_0+\left[\begin{array}{ccc} E_{0, \mathrm{f}} & 0 & 0 \\ 0 & E_{0, \mathrm{p}} & 0 \\ 0 & 0 & E_{0, \mathrm{~g}} \end{array}\right] \cdot \boldsymbol{M} \cdot\left[\begin{array}{c} \Delta e_{\mathrm{f}} / e_0 \\ \Delta e_{\mathrm{p}} / e_0 \\ \Delta e_{\mathrm{g}} / e_0 \end{array}\right] \\ & =\left[E_{\mathrm{f}}, E_{\mathrm{p}}, E_{\mathrm{g}}\right]^{\mathrm{T}} \end{aligned} $ | (4) |
式中:E0——实行分时电价前电量,E0=[E0,f,E0,p,E0,g]T;
E0,f,E0,p,E0,g——实行分时电价前峰、平、谷时段电量;
∆ef,∆ep,∆eg——实行分时电价后峰、平、谷时段电价变化量;
e0——实行分时电价前电价;
Ef,Ep,Eg——实行分时电价后峰、平、谷时段电量。
2 风力发电与AA-CAES系统模型
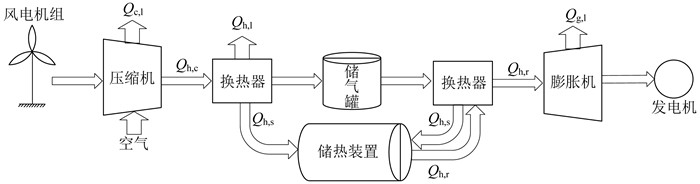
2.1 风力发电与AA-CAES系统结构
2.2 风力发电系统模型
以双馈异步风力发电机为例,考虑其发电量随风速变化的不确定性,假设实际风速ν服从Weibull分布[20],分布函数公式如下:
| $ g(v)=\frac{k}{c^k} v^{k-1} \mathrm{e}^{-\left(\frac{v}{c}\right)^k} $ | (5) |
式中:g(ν)——Weibull分布函数;
k——描述风速分布范围与形状的参数;
c——年平均风速。
此时风机的输出功率PW为
| $ P_{\mathrm{W}}=\left\{\begin{array}{lr} 0, & \text { 其他 } \\ P_{\mathrm{e}} \frac{v-v_{\text {in }}}{v_{\mathrm{e}}-v_{\text {in }}}, & v_{\text {in }}<v \leqslant v_{\mathrm{e}} \\ P_{\mathrm{e}}, & v_{\mathrm{e}}<v \leqslant v_{\text {out }} \end{array}\right. $ | (6) |
式中:Pe——风机的额定输出功率;
vin——风机的切入风速;
ve——风机的额定风速;
vout——风机的切出风速。
2.3 AA-CAES系统模型
本文对AA-CAES系统的建模基于以下假设:压缩机和膨胀机内的气体采用理想气体模型;不考虑气体在流动过程中的热量损失。
系统采用N级压缩,根据压缩机功耗表达式,可得压缩过程的功率表达式[21]为
| $ P_{\mathrm{c}}(t)=\eta_{\mathrm{c}} m_{\mathrm{a}} c_{\mathrm{a}} \sum\limits_{i=1}^N T_{\mathrm{o}}\left[\beta_{\mathrm{c}}^{(\gamma-1) /(\gamma i)}-1\right] $ | (7) |
式中:Pc (t)——t时段压缩机压缩功率;
ηc——压缩机效率;
ma——空气质量;
ca——空气定压比热容;
T0——环境温度;
βc——压缩机的额定压缩比;
γ——空气的比热容。
压缩空气储能释放能量时,将气体升温,此时高温、高压气体膨胀实现做功发电。因此,系统膨胀功率的表达式为
| $ P_{\mathrm{d}}(t)=\eta_{\mathrm{t}} m_{\mathrm{a}} c_{\mathrm{a}} \sum\limits_{i=1}^N T_{\mathrm{u}}\left[1-\beta_{\mathrm{d}}^{-(\gamma-1) /(\gamma i)}\right] $ | (8) |
式中:Pd (t)——t时段膨胀机膨胀功率;
ηt——膨胀机效率;
Tu——升温后空气温度;
βd——膨胀机的额定膨胀比。
3 目标函数模型及求解方法
3.1 目标函数
针对风力发电与AA-CAES系统中计及分时电价的容量配置问题以及成本目标,通过合理安排各单元出力,使运行成本最低。系统总成本F包括固定成本Fc、设备维护成本Fp、购电成本Fg、售电收益Fs以及调峰成本Ft,目标函数为
| $ \min F=F_{\mathrm{c}}+F_{\mathrm{p}}+F_{\mathrm{g}}-F_{\mathrm{s}}+F_{\mathrm{t}} $ | (9) |
固定成本包括风电机组与AA-CAES系统的装机费用、土地成本等,公式为
| $ F_{\mathrm{c}}=\sum\limits_{t_1=1}^n \frac{F_{\mathrm{N}, t_1}+0.8 F_1}{(1+r)^{t_1}} $ | (10) |
式中:t1——经营年数;
n——总经营期年数;
FN,t1——第t1年成本;
F1——上一监管周期风力发电系统的年运行收益,根据规定,年运行收益的80% 在下一监管周期核定风力发电系统容量电价时扣除;
r——时间折算系数。
运行过程中各设备维护成本为
| $ F_{\mathrm{p}}=\sum\limits_{t=1}^T\left[\sum\limits_{j=1}^M C_j\left|P_j(t)\right|\right] $ | (11) |
式中:T——运行总小时数;
M——设备编号总数;
Cj——设备j的单位维护费用;
Pj (t)——t时段设备j的输出功率。
电量缺额情况下从电网购电的购电成本为
| $ F_{\mathrm{g}}=\sum\limits_{t=1}^T\left[C_{\mathrm{g}}(t) P_{\mathrm{gx}}(t)\right] $ | (12) |
式中:Cg (t)——t时段内的购电价格;
Pgx (t)——t时段内的购电功率。
电量富余情况下向电网售电的售电收益为
| $ F_{\mathrm{s}}=\sum\limits_{t=1}^T\left[C_{\mathrm{s}}(t) P_{\mathrm{sx}}(t)\right] $ | (13) |
式中:Cs (t)——t时段内的售电价格;
Psx (t)——t时段内的售电功率。
为了验证实行分时电价后负荷的转移效果,讨论分时电价的削峰填谷能力,本文引入了负荷的调峰成本这一概念。负荷的调峰成本采用所有时段负荷峰谷差平方之和来表示,并通过引入经济折算系数ζ将负荷调峰目标映射到经济维度。由于经济折算系数ζ可调,因此取值的大小反映了分时电价削峰填谷能力在系统目标函数中的重要性,以及对目标函数影响的大小。调峰成本与系统其他成本一起构成系统总成本。这样既考虑到了负荷削峰填谷的效果,又兼顾了经济性[22]。实行分时电价后调峰成本为
| $ F_{\mathrm{t}}=\sum\limits_{t=1}^T \zeta\left[P_{\mathrm{L}}(t)-\bar{P}_{\mathrm{L}}(t)\right]^2 $ | (14) |
式中:PL (t)——系统在t时段的负荷功率;
PL (t)——系统平均负荷功率。
3.2 约束条件
(1)压缩功率约束条件:
| $ P_{\mathrm{c}}^{\min }(t) v_{\mathrm{c}}(t) \leqslant P_{\mathrm{c}}(t) \leqslant P_{\mathrm{c}}^{\max }(t) v_{\mathrm{c}}(t) $ | (15) |
式中:Pcmin (t),Pcmax (t)——压缩功率的下限和上限;
νc (t)——二进制数值,取值为0或1,AA-CAES系统t时段处于压缩工况时取1,反之取0。
(2)膨胀功率约束条件:
| $ P_{\mathrm{d}}^{\min }(t) v_{\mathrm{d}}(t) \leqslant P_{\mathrm{d}}(t) \leqslant P_{\mathrm{d}}^{\max }(t) v_{\mathrm{d}}(t) $ | (16) |
式中:Pdmin (t),Pdmax (t)——膨胀功率的下限和上限;
νd (t)——二进制数值,取值为0或1,AA-CAES系统t时段处于膨胀工况时取1,反之取0。
(3)AA-CAES系统运行工况约束条件:
| $ v_{\mathrm{c}}(t) v_{\mathrm{d}}(t)=0 $ | (17) |
νc (t)、νd (t) 均为二进制数,式(17)中的约束条件保证了AA-CAES系统可以选择在压缩工况或膨胀工况下单独工作。
(4)储热装置约束条件:
| $ 0 \leqslant Q_{\mathrm{TES}} \leqslant Q_{\mathrm{TES}}^{\max } $ | (18) |
式中:QTES,QTESmax——储热装置中储热量及其上限。
(5)AA-CAES系统电量约束条件:
| $ E_{\min } \leqslant E(t) \leqslant E_{\max } $ | (19) |
| $ E_{\max }=95 \% E_{\mathrm{B}} $ | (20) |
| $ E_{\min }=5 \% E_{\mathrm{B}} $ | (21) |
式中:Emin,Emax——AA-CAES系统电量的最小值和最大值;
E(t)——AA-CAES系统电量;
EB——AA-CAES系统电量的初始容量。
(6)储气罐约束条件:
| $ S_{\mathrm{OC}}(t+1)=S_{\mathrm{OC}}(t)+\frac{v_{\mathrm{c}}(t) P_{\mathrm{c}}(t) \Delta t-v_{\mathrm{d}}(t) P_{\mathrm{d}}(t) \Delta t}{E_{\max }} $ | (22) |
| $ S_{\mathrm{OC}}^{\min } \leqslant S_{\mathrm{OC}}(t) \leqslant S_{\mathrm{OC}}^{\max } $ | (23) |
式中:SOC (t+1),SOC (t)——储气室在t+1时段和t时段的状态;
SOCmin,SOCmax——储气室SOC的最小值和最大值;
∆t——时间间隔,取1 h。
(7)功率平衡约束条件:
| $ P_{\mathrm{L}}(t)=P_{\mathrm{W}}(t)+P_{\mathrm{d}}(t) v_{\mathrm{d}}(t)-P_{\mathrm{c}}(t) v_{\mathrm{c}}(t) $ | (24) |
式中:PW (t)——t时段风电机组的输出功率。
3.3 求解方法
风力发电与AA-CAES系统的容量配置问题属于多阶段最优化决策问题,因此采用动态规划法,以一年内(8 760 h)的等效负荷平方和最小为目标对AA-CAES系统的压缩、膨胀功率进行优化[23],得到风力发电与AA-CAES系统的最优容量配置如图 2所示。
基本思想是将容量配置分解为若干个阶段,按顺序求解每一阶段的最优容量,根据约束条件列出各种可能的局部解,通过决策保留那些有可能达到最优容量配置的值,丢弃其他局部解。依次解决各子问题,最后一个子问题f的解就是系统最优容量。
系统最优容量对应的求解公式为
| $ f=\min \sum\limits_{t=1}^{8760}\left[P_{\mathrm{L}}(t)-P_{\mathrm{W}}(t)+P_{\mathrm{A}}(t)\right]^2 $ | (25) |
式中:PA (t)——t时段AA-CAES系统的压缩/膨胀功率,当PA (t) > 0时表示压缩功率,当PA (t) < 0时表示膨胀功率。
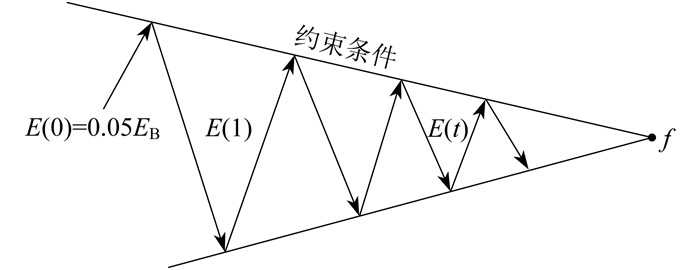
综上所述,将AA-CAES系统的压缩、膨胀过程看成动态规划里的一个子阶段,初始状态E(0) = 0.05EB,t时段后的递推方程为
| $ f[E(t)]=\min\limits_{u(t) \in d(P(t))} f\left\{E(t-1)+v_{\mathrm{n}}[E(t), u(t)]\right\} $ | (26) |
式中:u(t)——t时段的决策变量;
d(P(t))——由P(t) 和容量约束等确定的允许决策集合;
υn [E(t),u(t)]——等效负荷平方和函数。
因此,先从第一个子问题出发,找到最后一个子问题式(25)对应的最小值后,再从最后一个子问题出发,寻找每个时段AA-CAES系统的压缩、膨胀功率。
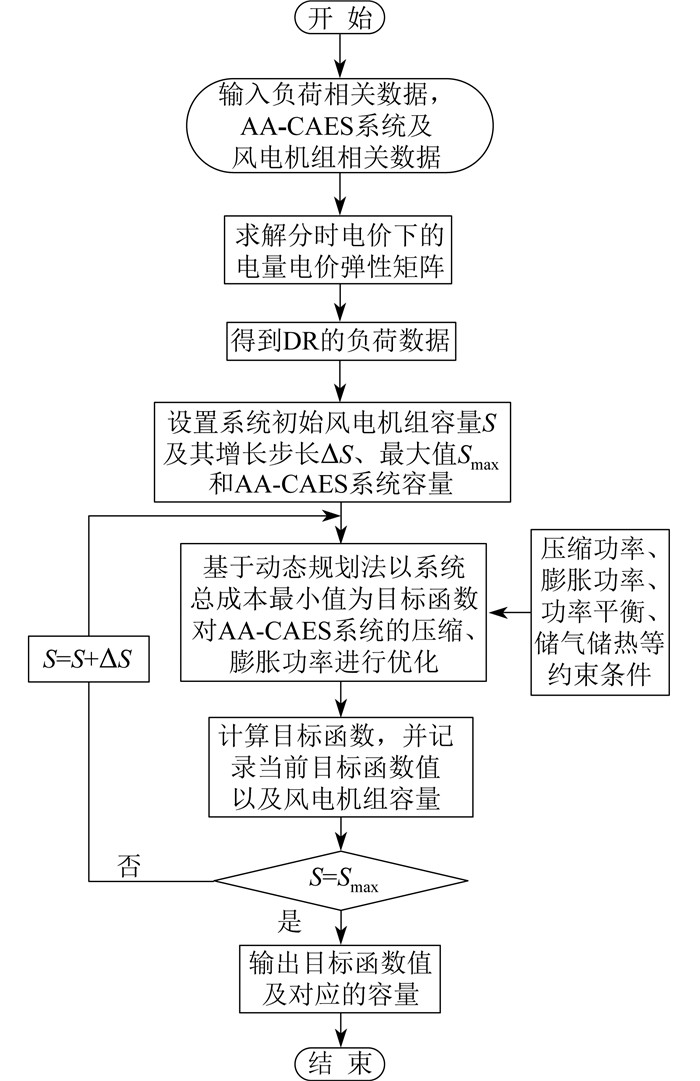
综合以上动态规划法求解思想,考虑约束条件下的目标函数模型求解流程如图 3所示。
4 算例分析
4.1 算例参数
本文以某地一年的负荷为例,研究DR对风力发电与AA-CAES系统的影响。
基于MATLAB平台,通过动态规划法对此问题进行求解。风电机组单位功率建设成本为6 500元/kW,年利率为5%,经营期为40 a,还款期限为25 a,维护费用为0.15元/kW,Weibull分布的参数c=7.5 m/s、k=2。AA-CAES电站的建设成本为4 500元/kW,维护费用为0.019 6元/kW。基于文献[17]中的需求弹性系数,取峰、平、谷时段电量-电价曲线参数af、bf、ap、bp、ag、bg分别为6.5、65、5.0、60、4.0、58。分时电价如表 1所示。风电机组和AA-CAES系统的各项参数分别如表 2和表 3所示。本文以表 2和表 3的参数对风力发电与AA-CAES系统进行建模与约束条件分析。
表 1
分时电价
| 时段类型 | 时段 | 购电价格 | 售电价格 |
| 峰 | 10:00—15:00 | 0.80 | 0.68 |
| 17:00—22:00 | |||
| 平 | 07:00—10:00 | 0.60 | 0.50 |
| 15:00—17:00 | |||
| 22:00—24:00 | |||
| 谷 | 00:00—07:00 | 0.30 | 0.26 |
表 2
风电机组参数
| 参数 | 取值 |
| 单机容量/MW | 1 |
| 切入风速/(m/s) | 3 |
| 额定风速/(m/s) | 12 |
| 切出风速/(m/s) | 25 |
表 3
AA-CAES系统参数
| 参数 | 取值 |
| 环境温度/K | 293 |
| 压缩机效率 | 0.75 |
| 膨胀机效率 | 0.8 |
| 空气质量/kg | 1 |
| 空气定压比热容/[J/(kg·K)] | 1 000 |
| 空气的比热容 | 1.4 |
| 压缩机的额定压缩比 | 5 |
| 储热装置中储热量上限/MJ | 2.0×106 |
4.2 DR分析
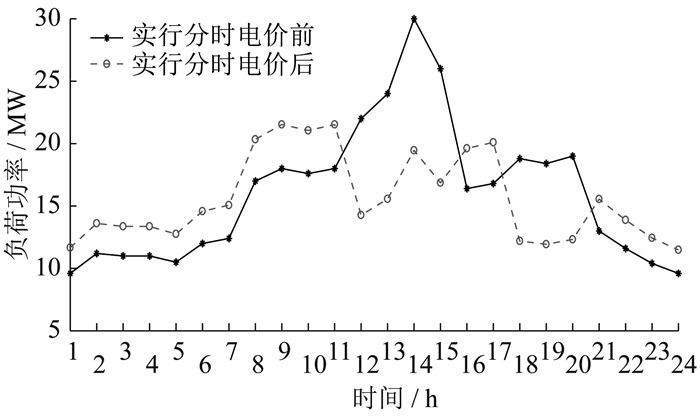
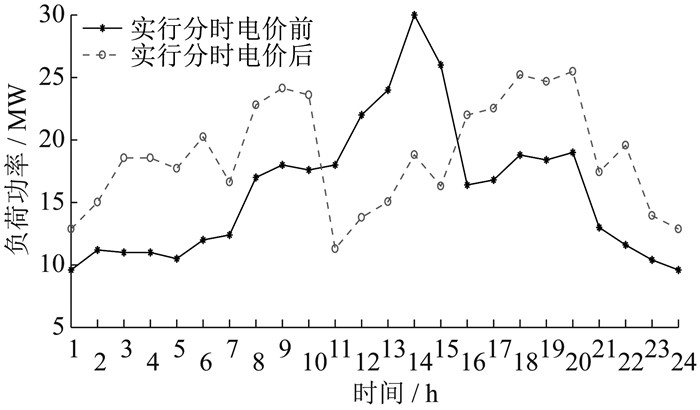
根据以上数据可得电量电价弹性矩阵 M,实行分时电价前后日负荷曲线如图 4所示。
由图 4可知,实行分时电价后负荷的峰谷差减小。经济折算系数ζ设为1 000,计算得到实行分时电价前调峰成本为3.065×105元,实行分时电价后调峰成本为1.225×105元,调峰成本减少了约60%,达到了削峰填谷的效果。与此同时,导入一年的负荷数据进行计算,得到实行分时电价前系统总成本最小值为4.226×108元,实行分时电价后系统总成本最小值为3.749×108元减少了约11.3%。
电力负荷一般针对工业、商业、居民3类用户实行不同的分时电价。由于各类用户具有不同的特性,因此相应的峰、平、谷时段的分时电价也存在差异。表 1为居民型负荷实行的分时电价,下面讨论工业和商业型负荷实行分时电价前后用户的响应特性。工业和商业型负荷分时电价如表 4所示。
表 4
工业和商业型负荷分时电价
| 用户类型 | 时段类型 | 时段 | 购电价格/(元/kWh) |
| 工业 | 峰 | 08:00—16:00 | 1.22 |
| 平 | 06:00—08:00 | 0.60 | |
| 16:00—21:00 | |||
| 谷 | 21:00—24:00 | 0.47 | |
| 0:00—06:00 | |||
| 商业 | 峰 | 09:00—19:00 | 1.16 |
| 平 | 06:30—09:00 | 0.60 | |
| 19:00—24:00 | |||
| 谷 | 0:00—06:30 | 0.53 |
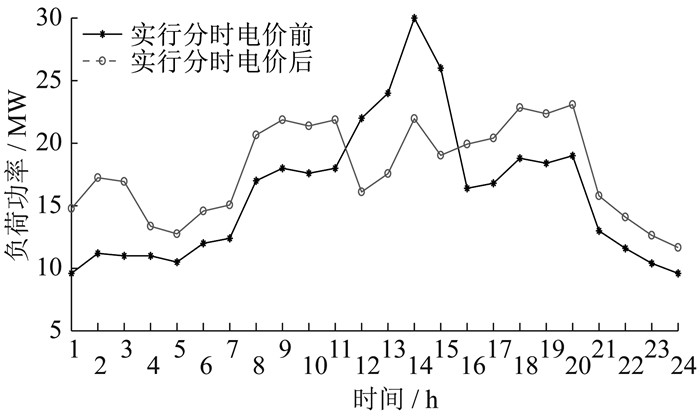
工业和商业型负荷实行分时电价前后日负荷曲线分别如图 5和图 6所示。
由图 5和图 6可知,与图 4的居民型负荷相比,工业和商业型负荷分时电价峰谷更加明显,因而负荷的转移量更明显,削峰填谷效果更好。
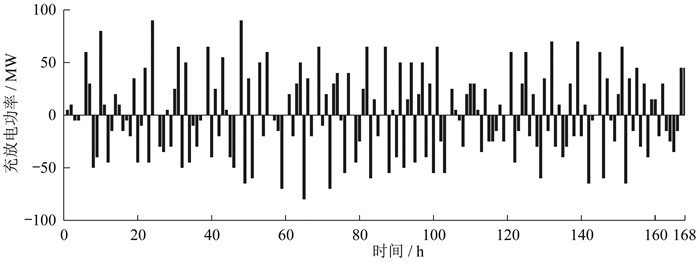
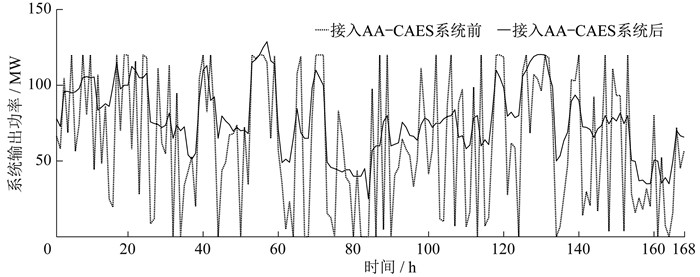
4.3 AA-CAES系统分析
4.4 风力发电与AA-CAES系统容量配置分析
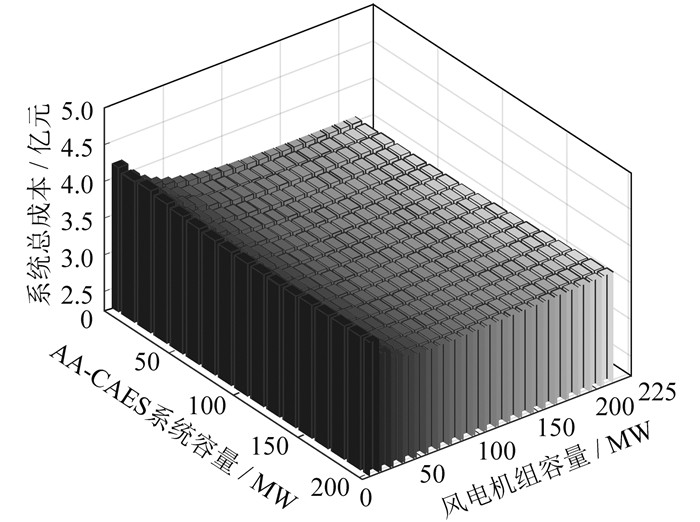
为了比较不同容量配置对系统目标函数的影响,本文根据风力发电与AA-CAES系统的不同容量配置绘制了图 9。由图 9可以看出,系统总成本存在一个最低点,此时为最优容量配置状态,将风速设置为7.5 m/s,通过计算得到此时AA-CAES系统容量为85 MW,风电机组容量为120 MW,系统总成本最小值为3.749×108元。
为了对比容量配置对目标函数的影响设置了4种不同场景。场景1:AA-CAES系统容量、风电机组容量与最优容量一致;场景2:AA-CAES系统容量为最优容量,风电机组容量大于最优容量;场景3:AA-CAES系统容量小于最优容量,风电机组容量为最优容量;场景4:AA-CAES系统容量、风电机组容量皆小于最优容量。
根据不同场景得到的整个系统总成本最小值如表 5所示。
表 5
不同场景对应的整个系统总成本最小值
| 场景 | AA-CAES系统容量/MW | 风电机组容量/MW | 整个系统总成本最小值/亿元 |
| 1 | 85 | 120 | 3.749 |
| 2 | 85 | 140 | 3.763 |
| 3 | 60 | 120 | 3.811 |
| 4 | 60 | 90 | 3.933 |
由表 5可知,风力发电与AA-CAES系统的容量规模会对整个系统总成本造成影响,即:在最优容量范围内,系统容量规模越大,对风电的消纳能力越强,整个系统总成本越低;但当系统容量增加超过最优容量时,整个系统总成本升高;当容量配置为最优时整个系统总成本最低。
不同年平均风速与AA-CAES系统容量、整个系统总成本最小值之间的对应关系如表 6所示。
表 6
不同风速对应的整个系统总成本最小值
| 年平均风速/(m/s) | AA-CAES系统容量/MW | 整个系统总成本最小值/亿元 |
| 5 | 150 | 4.732 |
| 6 | 100 | 4.062 |
| 7 | 90 | 3.838 |
| 8 | 80 | 3.675 |
| 9 | 70 | 3.545 |
由表 6可知,风资源越充沛,即系统所在地区的年平均风速越大,需要配置的AA-CAES系统容量越低,此时的整个系统总成本也越低。因此,将年平均风速设置为9 m/s,此时AA-CAES系统容量为70 MW,风电机组容量为100 MW,整个系统总成本最小值为3.545亿元,风力发电与AA-CAES系统容量规模和系统总成本皆低于年平均风速为7.5 m/s时。
5 结语
本文考虑DR对电力系统负荷的影响,通过分时电价政策,对负荷的削峰填谷起到了显著作用。采用动态规划法对AA-CAES系统压缩、膨胀功率进行优化,平抑了风电波动,提高了风电的利用率和系统的灵活性。针对某地一年的负荷,以整个系统总成本最低为目标优化配置了风力发电与AA-CAES系统容量,并通过仿真得到不同风资源即不同年平均风速时AA-CAES系统容量配置规模和整个系统总成本最小值。
本文只考虑了不同时段的电价对负荷需求的影响,并且全部负荷都响应电价变化。在后续工作中,应进一步考虑负荷中不参与分时电价政策的用户、断电赔偿等因素,以及在AA-CAES系统运行中频繁压缩、膨胀对系统设备寿命的影响。
参考文献
-
[1]阮前途, 陈赟, 潘智俊. 新型电力系统对实现沿海城市双碳目标贡献的探讨[J]. 电力系统自动化, 2022, 46(14): 11-18.
-
[2]舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1-9.
-
[3]EL-KHATTAM W, BHATTACHARYA K, HEGAZY Y, et al. Optimal investment planing for distributed generation in a competitive electricity market[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1674-1684. DOI:10.1109/TPWRS.2004.831699
-
[4]黎静华, 骆怡辰, 杨舒惠, 等. 可再生能源电力不确定性预测方法综述[J]. 高电压技术, 2021, 47(4): 1144-1155.
-
[5]MADAENI S H, SIOSHANSI R, DENHOLM P. How thermal energy storage enhances the economic viability of concentrating solar power[J]. Proceedings of the IEEE, 2012, 100(2): 335-347. DOI:10.1109/JPROC.2011.2144950
-
[6]梅生伟, 李瑞, 陈来军, 等. 先进绝热压缩空气储能技术研究进展及展望[J]. 中国电机工程学报, 2018, 38(10): 2893-2907.
-
[7]尹斌鑫, 苗世洪, 李姚旺, 等. 先进绝热压缩空气储能在综合能源系统中的经济性分析方法[J]. 电工技术学报, 2020, 35(19): 4062-4075.
-
[8]GUO C, PAN L, ZHANG K, et al. Comparison of compressed air energy storage process in aquifers and caverns based on the Huntorf CAES plant[J]. Applied Energy, 2016, 181: 342-356. DOI:10.1016/j.apenergy.2016.08.105
-
[9]杜鹏, 崔浩杰. 压缩空气储能商业电站在山东肥城并网[N]. 国家电网报, 2021-08-09(3).
-
[10]DIELMANN K, VAN DER VELDEN A. Virtual power plants (VPP)-a new perspective for energy generation?[C]//Proceedings of the 9th International Scientific and Practical Conference of Students, Post-graduates and Young Scientists (MTT 2003). Tomsk, Russia: IEEE, 2003: 18-20.
-
[11]MOHAMMED S S, TITUS F, THANIKANTI S B, et al. Charge scheduling optimization of plug-in electric vehicle in a PV powered grid-connected charging station based on dayahead solar energy forecasting in Australia[J]. Sustainability, 2022, 14(6): 13-20.
-
[12]SONY Y Q, SHANGGUAN L Z, LI G J. Simulation analysis of flexible concession period contracts in electric vehicle charging infrastructure pub-lic-private-partnership (EVCI-PPP) projects based on time-of-use (TOU) charging price strategy[J]. Energy, 2021, 228(8): 45-50.
-
[13]ZHANG C, XU Y, DONG Z Y, et al. Robust coordination of distributed generation and price-based demand response in micro grids[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4236-4247. DOI:10.1109/TSG.2017.2653198
-
[14]KHODAEI A, SHAHIDEHPOUR M, BAHRAMIRAD S. SCUC with hourly demand response considering intertemporal load characteristics[J]. IEEE Transactions on Smart Grid, 2011, 2(3): 564.
-
[15]王守相, 王瀚樟, 赵倩宇, 等. 面向配电网光伏接纳能力提升的分时电价优化方法[J]. 电力系统自动化, 2023, 47(10): 38-46.
-
[16]陈倩, 王维庆, 王海云. 计及需求响应和混合博弈含多微网主动配电网协调优化[J]. 电力系统自动化, 2023, 47(9): 99-109.
-
[17]秦祯芳, 岳顺民, 余贻鑫. 零售端电力市场中的电量电价弹性矩阵[J]. 电力系统自动化, 2004, 28(5): 16-19.
-
[18]陈沧杨, 胡博, 谢开贵, 等. 计入电力系统可靠性与购电风险的峰谷分时电价模型[J]. 电网技术, 2014, 38(8): 2141-2148.
-
[19]吴晨曦, 陈泽昊, 张杰, 等. 考虑先进绝热压缩空气储能的风力发电系统成本/供电可靠性评估[J]. 电力自动化设备, 2020, 40(2): 62-68.
-
[20]黄伟, 杨舒文, 葛良军. 基于概率潮流的主动配电网供需群体协同优化运行策略[J]. 电力系统自动化, 2017, 41(13): 39-44.
-
[21]王成山, 武震, 杨献莘, 等. 基于微型压缩空气储能的混合储能系统建模与实验验证[J]. 电力系统自动化, 2014, 38(23): 22-26.
-
[22]卫志农, 张思德, 孙国强, 等. 计及电转气的电-气互联综合能源系统削峰填谷研究[J]. 中国电机工程学报, 2017, 37(16): 4601-4609.
-
[23]吴晨曦, 文福拴, 李梅. 计及储能系统充放电策略的风光混合发电系统容量优化[J]. 华北电力大学学报(自然科学版), 2014, 41(4): 22-29.