|
|
|
发布时间: 2024-06-28 |
综合能源 |
|
|
|
收稿日期: 2024-01-18
基金项目: 国家自然科学基金(52177184)
中图法分类号: TM744; TM711
文献标识码: A
文章编号: 2096-8299(2024)03-0220-07
|
摘要
氢能作为清洁能源,可与风能等可再生能源结合,为系统提供低碳运行方案。首先,在传统电氢耦合系统的基础上,引入天然气及碳捕集系统,设计了计及氢能多元利用特性的电氢能源系统优化配置模型。然后,建立了将氢能零污染发电和甲烷化两种应用途径相结合的系统模型,以系统等年值成本最小为目标函数,通过改进粒子群算法对构建模型进行寻优求解,得到了系统各设备最优容量配置方案。最后,通过算例对比,证明了优化方案在成本最低时,可支配碳配额增加,具有环保性。
关键词
电氢耦合; 低碳运行; 优化配置; 改进粒子群算法
Abstract
Hydrogen energy, as a clean energy source, can be combined with renewable energy such as wind energy to provide low-carbon operation solutions for the system. First, on the basis of the traditional electro-hydrogen coupling system, this paper introduces natural gas and carbon capture system, and proposes an optimal configuration model method for electro-hydrogen energy system considering the characteristics of multiple utilization of hydrogen energy. Then, a system model combining the two application approaches of hydrogen energy zero-pollution power generation and methanation is established, and the improved particle swarm optimization algorithm is proposed to optimize and solve the construction model with the annual cost of the system as the objective function, so as to obtain the optimal capacity configuration scheme of each equipment in the system. Finally, the comparative analysis of the example shows that the optimization scheme increases the disposable carbon quota when the cost is the lowest, which is environmentally friendly.
Key words
electro-hydrogen coupling; low-carbon operation; optimization allocation; improved particle swarm algorithm
2020年,我国明确提出了力争于2030年前实现二氧化碳排放达到峰值,2060年前实现碳中和的目标。电力行业的碳排放量在我国总排放量中占比居高不下,建立以新能源为主体的新型电力系统成为主要发展方向[1]。风能作为丰富的可再生能源,具有间歇性和波动性等特征[2]。风电大规模并网给新型电力系统的安全、稳定运行带来了巨大挑战。氢能作为高热值、易存储、易获取的二次能源,可在能源互联网之间灵活转换,协助工业、交通、建筑、航空航天等领域减排[3]。氢能在能源转换和平抑微电网波动方面具有较高的应用价值,以氢能为主的电氢耦合微电网成为近几年的研究热点。
设备容量配置是微电网前期规划的重要环节。文献[4]综合考虑风电场功率的不确定性和氢能设备投资成本,基于风电场真实场景验证,提高了氢能系统的实际可用容量。文献[5]考虑了制氢效率特性、售电和售氢收益、投资运维成本和弃风成本,以风氢系统收益最大化为目标,实现了最经济的风氢系统容量优化配置。文献[6]同时考虑了购电成本和售电利润,采用混合算法降低了系统的净现值成本,表明氢能系统可以较好地平抑可再生能源波动。文献[7]运用阶梯碳交易机制对上级电网购买的火电和系统本身产生的碳排放进行抑制,并考虑需求响应,建立双层模型,得到年化成本最小时的微电网低碳运行容量配置方案。文献[8]在文献[7]的基础上,在电氢能源系统鲁棒规划模型中引入阶梯碳交易机制,引导系统控制碳排放量,有效提高了新能源的消纳。文献[9]在考虑阶梯碳交易的基础上,将碳捕集和氢气甲烷化纳入综合能源微电网,通过购入氢气和碳捕集二氧化碳反应生成甲烷,实现了低碳运行,并将多余碳排放配额出售,提高了系统经济性。文献[10]基于微电网能源集线器模型,研究了P2G多源储能对风电消纳能力的影响,并采用氢能系统作为中间环节,减小电网富余能量流向天然气网络的冲击作用,提高了新能源消纳能力。
综上所述,当前针对微电网容量优化的研究主要集中于燃料电池的用氢途径,而综合能源微电网着重考虑的是氢气甲烷化的电转气利用。本文在现有研究基础上,综合考虑燃料电池发电和氢气甲烷化两种方式,通过燃气轮机将制取的甲烷加以利用,降低系统碳排放,提高新能源消纳。
1 计及氢能多元利用特性的电氢耦合系统模型
本文提出的计及氢能多元利用特性的电氢耦合系统结构如图 1所示。
系统用电需求由上级电网、碳捕集电厂、风电机组、氢燃料电池及燃气轮机提供。其中,由于燃气轮机产生的二氧化碳浓度较低、捕集成本高,因此直接排放。鉴于风电的波动性和间歇性,本文未考虑向上级电网售电,各设备产能仅在系统内部消纳。为充分发挥系统供电潜力和氢能多元利用优势,本文优先考虑风电机组出力,然后再考虑为燃气轮机和氢燃料电池供电。只有当系统内部设备无法承担电网负荷要求时,再考虑从上级电网购电,以维持微电网功率平衡。
本文所提系统中风力发电机、碳捕集设备和燃气轮机的数学模型参考文献[11-12]。该系统在传统电氢耦合系统的基础上,计及氢能多元利用特性,综合考虑氢能发电和氢气甲烷化两种用能途径。当风电富余时,氢气用于甲烷化生成天然气;当负荷过载时,储氢罐输出氢气以备燃料电池发电使用。其中,氢储能系统由质子交换膜电解槽、储氢罐及质子交换膜燃料电池组成。质子交换膜电解槽和质子交换膜燃料电池为电氢耦合设备,可实现电氢相互转换。系统中的甲烷化设备可将氢气转换成天然气,与氢储能系统配合,实现氢能多元利用。
1.1 质子交换膜电解槽模型
常用电解槽包括碱性水电解槽、固体氧化物电解槽和质子交换膜电解槽。本文采用质子交换膜电解槽,其结构紧凑、制氢效率高,可将多余风电转换成氢气。质子交换膜电解槽的产氢计算公式[13]为
| $ m_{s, t}^{\mathrm{el}}=P_{\mathrm{el}}(t) \cdot \frac{\rho_{\mathrm{H}}}{\eta_{\mathrm{el}} h} $ | (1) |
式中:ms, tel——场景s下,t时段电解槽产生的氢气质量;
Pel (t)——t时段电解槽工作功率;
ρH,h——氢气的密度和热值;
ηel——电解槽运行效率。
1.2 储氢罐模型
在传统电氢耦合系统中,储氢罐仅用于日常储存电解槽生产的氢气,以及在负荷超载时为燃料电池提供氢气燃料。在本文所提系统中,由于考虑氢能多元利用特性,储氢罐除承担上述功能外,还需在风电富余时为甲烷化设备提供氢气。储氢罐储氢量计算公式为
| $ E_{\mathrm{hst}}(t+\Delta t)=E_{\mathrm{hst}}(t)+P_{\mathrm{el}}(t) \eta_{\mathrm{el}} \Delta t-m_t^{\mathrm{H}_2} \frac{\eta_{\mathrm{el}} h}{\rho_{\mathrm{H}} \eta_{\mathrm{hst}}} $ | (2) |
| $ E_{\text {hst }}(t+\Delta t)=E_{\text {hst }}(t)-\frac{P_{\mathrm{fc}}(t)}{\eta_{\mathrm{fc}} \eta_{\mathrm{hst}}} \Delta t $ | (3) |
式中:Ehst (t+∆t),Ehst (t)——t+∆t和t时段储氢罐的储氢量;
mtH2——t时段甲烷化设备的氢气消耗质量;
Pfc (t)——t时段燃料电池工作效率;
ηhst,ηfc——储氢罐和燃料电池效率。
1.3 燃料电池模型
质子交换膜燃料电池发电量与氢气消耗量之间的关系[14]为
| $ P_{\mathrm{fc}}(t)=\eta_{\mathrm{fc}} \frac{v_{\mathrm{fc}}(t)}{\mu_{\mathrm{fc}}} $ | (4) |
式中:vfc (t)——t时段燃料电池消耗氢气的速率;
μfc——燃料电池生产单位电量消耗的氢气。
1.4 甲烷化设备模型
甲烷化设备是电转气技术的重要部分,可将氢气和二氧化碳反应生成天然气和水,其与燃料电池配合可实现氢能多元利用,具体技术细节参考文献[12]。其中,二氧化碳、氢气、甲烷的摩尔质量比为1∶4∶1。氢气甲烷化反应中二氧化碳、氢气、甲烷的质量关系为
| $ m_t^{\mathrm{CH}_4}=\frac{M_{\mathrm{CH}_4}}{M_{\mathrm{CO}_2}} \cdot m_t^{\mathrm{CO}_2} \cdot\left(1-\omega_{\mathrm{MR}}\right) $ | (5) |
| $ m_t^{\mathrm{H}_2}=\frac{4 M_{\mathrm{H}_2}}{M_{\mathrm{CO}_2}} \cdot m_t^{\mathrm{CO}_2} \cdot\left(1-\omega_{\mathrm{MR}}\right) $ | (6) |
式中:mtCH4——t时段生成甲烷的质量;
mtH2,mtCO2——t时段氢气、二氧化碳消耗的质量;
MCO2,MCH4,MH2——二氧化碳、甲烷、氢气的摩尔质量;
ωMR——氢气甲烷化反应的损耗系数。
2 基于改进粒子群算法的容量优化配置
为体现电氢能源系统的经济性,本文以系统最小等年值成本为目标函数,考虑约束条件,并根据系统模型特点选择改进粒子群算法求解最优配置方案。
2.1 目标函数
电氢耦合系统以最小等年值成本Fmin为优化目标构建低碳经济模型。Fmin的计算公式为
| $ F_{\min }=F_{\mathrm{inv}}+F_{\text {main }}+F_{\mathrm{om}}+F_{\text {waste }} $ | (7) |
式中:Finv——等年值设备投资成本;
Fmain——等年值设备维护成本;
Fom——年运行成本;
Fwaste——弃风惩罚成本。
等年值设备投资成本Finv的计算公式为
| $ F_{\text {inv }}=\sum\limits_{k \in \mathit{\Omega }_k} C_{k, \text { inv }} P_k r^{\mathrm{CR}} $ | (8) |
式中:Ωk——设备k的集合,包括风力发电机、电解槽、储氢罐、燃料电池、燃气轮机共5类设备;
Ck,inv——设备k的单位容量或单位发电功率投资成本;
Pk——设备k的投资容量;
rCR——资金收回系数。
资金收回系数rCR的计算公式为
| $ r^{\mathrm{CR}}=\frac{\gamma(1+\gamma)^{y_k}}{(1+\gamma)^{y_k}-1} $ | (9) |
式中:γ——贴现率;
yk——设备k的运行周期。
等年值设备维护成本Fmain的计算公式为
| $ F_{\text {main }}=\sum\limits_{k \in \mathit{\Omega }_k} C_{k, \text { main }} P_k $ | (10) |
式中:Ck,main——设备k的单位容量或单位发电功率维护成本。
年运行成本Fom的计算公式为
| $ F_{\mathrm{om}}=\sum\limits_{s=1}^{12} \sum\limits_{t=1}^T \theta_s\left[\varepsilon_{\mathrm{buy}} P_{\mathrm{CF}}(t)+\left(\varepsilon_{\mathrm{b}}+\varepsilon_{\mathrm{c}}\right) c_{\mathrm{CO}_2}(t)\right] $ | (11) |
式中:θs——典型日s的场景权重;
T——时间周期;
εbuy——系统购电单价;
PCF (t)——t时段购电功率;
εb,εc——单位二氧化碳的捕集价格和封存价格;
cCO2 (t)——t时段碳捕集电厂释放的二氧化碳量。
弃风惩罚成本的计算公式为
| $ F_{\text {waste }}=\sum\limits_{s=1}^{12} \sum\limits_{t=1}^T \theta_s c_{\text {waste }}(t) $ | (12) |
式中:cwaste (t)——t时段系统产生的弃风量。
2.2 约束条件
2.2.1 功率平衡约束
电氢耦合系统需满足功率实时平衡。电能平衡约束公式为
| $ \begin{array}{l} P_{\mathrm{w}}(t)+P_{\mathrm{CF}}(t)+P_{\mathrm{GT}}(t)-P_{\text {waste }}(t)=P_{\mathrm{BJ}}(t)+P_{\mathrm{el}}(t)- \\ P_{\mathrm{fc}}(t)+P_{\mathrm{E}}(t) \end{array} $ | (13) |
式中:Pw (t)——t时段风机输出功率;
PGT (t)——t时段燃气轮机发电功率;
Pwaste (t)——t时段弃风发电量;
PBJ (t)——t时段碳捕集耗能;
PE (t)——t时段负荷功率。
2.2.2 设备出力约束
风机和燃气轮机设备出力满足的条件为
| $ 0 \leqslant P_{\mathrm{W}}(t) \leqslant P_{\mathrm{W}} $ | (14) |
| $ 0 \leqslant P_{\mathrm{GT}}(t) \leqslant P_{\mathrm{GT}} $ | (15) |
式中:PW,PGT——风机和燃气轮机的额定功率。
二氧化碳罐的储气约束条件为
| $ 0 \leqslant V_{\mathrm{CO}_2}(t) \leqslant V_{\mathrm{CO}_2, \max } $ | (16) |
式中:VCO2 (t),VCO2,max——t时段二氧化碳罐储气量和最大储气量。
2.2.3 氢储能系统约束
氢储能系统约束条件包括电解槽约束、燃料电池出力约束和储氢罐储氢量约束。约束条件为
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{el}}(t) \leqslant P_{\mathrm{el}} \\ 0 \leqslant P_{\mathrm{fc}}(t) \leqslant P_{\mathrm{fc}, \max } \\ V_{\mathrm{hst}, \min } \leqslant V_{\mathrm{hst}}(t) \leqslant V_{\mathrm{hst}, \max } \end{array}\right. $ | (17) |
式中:Pel——电解槽额定容量;
Pfc,max——燃料电池最大输出功率;
Vhst (t)——t时段储氢罐中储氢量;
Vhst,min,Vhst,max——储氢罐最小容量和最大容量。
2.3 混沌粒子群算法
本文提出的计及氢能多元利用特性的电氢耦合系统优化模型具有非线性、设备多和能源流向复杂等特点,使得目标函数优化求解难度很大,若采用常规算法求解会陷入局部最优、精度低等困境。为此,本文采用了一种基于混沌优化策略的改进粒子群算法。混沌粒子群优化(Chaotic Particle Swarm Optimization,CPSO)算法建立在粒子群优化(Prticle Swarm Optimization,PSO)算法基础上。PSO算法迭代过程中单个粒子速度和位置的更新公式[15]为
| $ V_{t+1}=W V_t+C_1\left(X_{\mathrm{pbest}}-X_t\right)+C_2\left(X_{\mathrm{gbest}}-X_t\right) $ | (18) |
| $ X_{t+1}=X_t+V_{t+1} $ | (19) |
式中:Vt,Vt+1——粒子群更新前后的速度;
W——粒子速度更新的惯性权重;
C1,C2——个体学习因子和群体学习因子;
Xpbest,Xgbest——粒子个体、种群的历史最佳位置;
Xt,Xt+1——粒子群更新前后的位置。
CPSO算法使用混沌优化策略扩大粒子搜索范围,从而克服了PSO算法容易陷入局部最优的问题。CPSO算法模型[16]为
| $ z(t+1)=\mu z(t)[1-z(t)] $ | (20) |
| $ x(t+1)=x_{\min }+z(t+1)\left(x_{\max }-x_{\min }\right) $ | (21) |
式中:z(t+1)——更新后属于[0, 1]的随机数;
μ——控制参数,一般取4;
z(t)——[0, 1]中的随机数;
xmax,xmin——粒子迭代过程中的极大值和极小值。
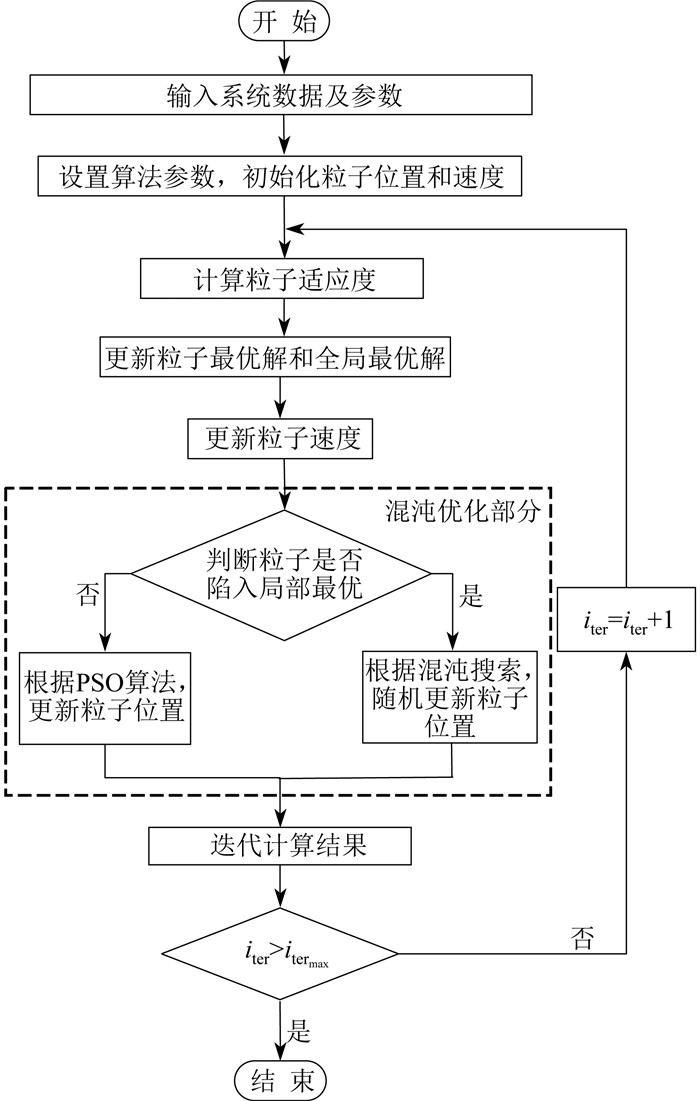
本文分别采用PSO和CPSO两种算法求解系统内设备容量的最优组合,以实现系统在安全运行下成本最小。CPSO算法流程如图 2所示。其中,iter为当前迭代次数,itermax为最大迭代次数。
3 算例验证与分析
3.1 典型日基础数据
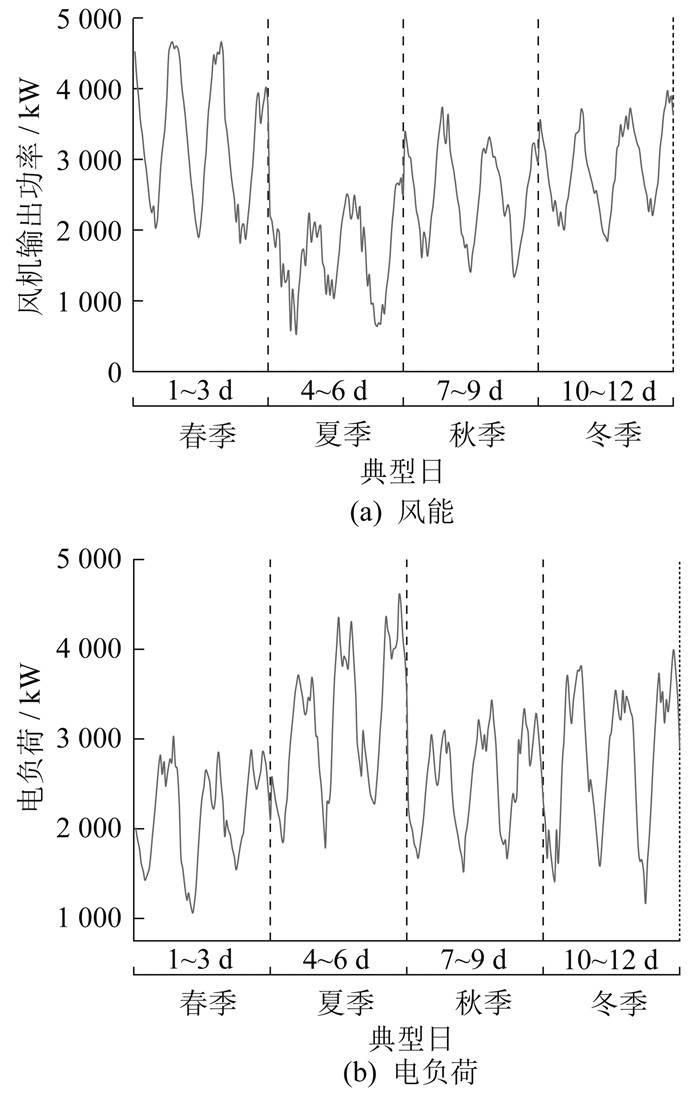
为了验证本文所建模型的正确性,以某地区微电网为例进行优化配置[17]。通过K-means聚类得到该地区4个季节共12个典型日的源荷曲线,具体如图 3所示。
系统参数数值与系统设备单位容量投资成本分别如表 1和表 2所示。
表 1
系统参数数值
| 参数 | 数值 | 参数 | 数值 | |
| 燃料电池单位耗氢量μfc/(kg/kW) | 0.06 | 碳捕集单位成本εb/(元/kg) | 1.2 | |
| 电解槽效率ŋel | 0.9 | 甲烷化损耗系数ωMR | 0.4 | |
| 储氢罐效率ŋhst | 1 | 设备k运行周期yk/a | 20 | |
| 燃料电池效率ŋfc | 0.5 | εbuy/(元/kWh) | 0.49 | |
| 贴现率γ | 0.1 | 碳封存单位成本εc/(元/kg) | 0.035 |
表 2
系统设备单位容量投资成本
| 设备名称 | 投资成本 | 维护成本 |
| 风力发电机 | 7 250 | 350 |
| 电解槽 | 6 000 | 300 |
| 储氢罐 | 15 000 | 450 |
| 燃料电池 | 3 000 | 150 |
| 燃气轮机 | 3 500 | 175 |
3.2 方案设计及分析
为对比分析计及氢能多元利用特性的电氢耦合系统的优势,共设置了2种方案对容量配置进行优化和分析。方案1为传统电氢耦合系统。方案2为计及氢能多元利用特性的电氢耦合系统。2种方案的容量配置与系统年化成本分别如表 3和表 4所示。
表 3
2种方案的容量配置
| 方案 | 风力发电机/kW | 电解槽/kW | 储氢罐/kg | 燃料电池/kW | 燃气轮机/kW |
| 1 | 4 270 | 1 616 | 3 612 | 3 184 | 0 |
| 2 | 4 310 | 1 802 | 3 549 | 2 677 | 1 003 |
表 4
2种方案的系统年化成本
| 方案 | 投资维护成本 | 运行成本 | 弃风惩罚成本 | 总成本 |
| 1 | 943.67 | 173.00 | 34.63 | 1 151.30 |
| 2 | 923.98 | 263.99 | 27.17 | 1 215.14 |
方案2同时考虑了氢燃料电池发电和氢气甲烷化两种能源利用途径,在方案1的基础上增加了碳捕集设备、氢气甲烷化装置及燃气轮机。由 表 4可以看出,氢能的多途径运用提高了新能源消纳,增加了风力发电机和电解槽容量,使得弃风惩罚成本减少了21.54%。燃气轮机的投入增加了系统发电设备种类,使得燃料电池配置容量下降,设备投资维护成本降低。虽然方案2增加了碳捕集和碳封存成本,使得系统总成本提高了5.54%,但考虑燃气轮机的热能效用,方案2仍有盈利。
为验证所提系统的环保性,本文将两种方案的碳排放额及碳排放量进行对比分析。计算方法参考文献[7]和文献[18]。2种方案的碳排放情况如表 5所示。
表 5
2种方案的碳排放情况
| 方案 | 燃煤电厂碳排放额 | 燃煤电厂碳排放量 | 燃气轮机碳排放额 | 燃气轮机碳排放量 | 碳排放总额 | 碳排放总量 |
| 1 | 2 570.24 | 3 813.00 | 0 | 0 | 2 570.24 | 3 813.00 |
| 2 | 2 113.42 | 313.53 | 260.97 | 230.39 | 2 374.39 | 543.92 |
由于方案1中不存在燃气轮机,因此认为方案1中全部碳排放额和碳排放量来源于上级电网[7]。方案2中碳排放额和碳排放量分别来源于燃煤电厂及燃气轮机。相较于方案1,方案2加装了甲烷化设备且购电量有所减少,因此碳排放总量下降了85.74%,碳排放总额下降了7.62%。由此可知,在相同的电负荷情况下,方案1需购入1 242.76 t碳排放额,而方案2中燃煤电厂富余1 830.47 t碳排放额。这表明在综合考虑氢能的两种能源利用途径后,方案2对于可再生能源的消纳能力增强,燃料电池担负电负荷和燃气轮机的发电量增加,购电量下降,可自由支配的碳排放额增加,在相同的碳排放总量下,燃煤电厂发电量增大。
从上述分析可知,综合考虑氢能多元利用特性后,系统可实现电氢联合运行,降低碳排放量,提高碳排放可支配额度,减少弃风现象。
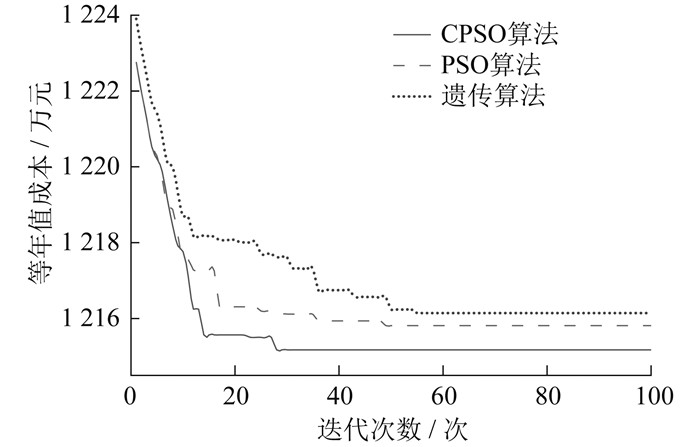
3.3 算法对比分析
4 结论
本文设计了计及氢能多元利用特性的电氢能源系统优化配置模型,并以系统等年值成本最小为目标函数,运用CPSO算法对目标函数进行求解,得到最优容量配置方案。通过对系统成本和碳排放情况进行对比分析,得到以下结论。
(1)计及氢能多元利用特性的电氢耦合系统弃风量减少,弃风惩罚成本降低21.54%,碳排放量减少84.44%,实现了二氧化碳捕集利用,降低了电转气设备的原料成本。
(2)计及氢能多元利用的电氢耦合系统可自由支配的碳排放额增多,在相同碳排放量下,提升了燃煤电厂发电量。
(3)CPSO算法不仅提高了算法的运算精度,同时实现了模型高效寻优,改善了PSO算法容易陷入局部最优的不足。
参考文献
-
[1]陈逸文, 赵晋斌, 李军舟, 等. 电力低碳转型背景下氢储能的挑战与展望[J]. 发电技术, 2023, 44(3): 296-304.
-
[2]EREN Y. Uncertainty-aware non-supplied load minimization oriented demand response program for PV/FC power system with electrolyzer back-up[J]. International Journal of Hydrogen Energy, 2022, 47(19): 10715-10735. DOI:10.1016/j.ijhydene.2022.01.072
-
[3]李军舟, 赵晋斌, 陈逸文, 等. 考虑动态功率区间和制氢效率的电转氢(P2H)设备容量配置优化[J]. 电工技术学报, 2023, 38(18): 4864-4874.
-
[4]司杨, 陈来军, 陈晓弢, 等. 基于分布鲁棒的风-氢混合系统氢储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 3-10.
-
[5]邓智宏, 江岳文. 考虑制氢效率特性的风氢系统容量优化[J]. 可再生能源, 2020, 38(2): 259-266.
-
[6]SAMY M M, MOSAAD M I, BARAKAT S. Optimal economic study of hybrid PV-wind-fuel cell system integrated to unreliable electric utility using hybrid search optimization technique[J]. International Journal of Hydrogen Energy, 2021, 46(20): 11217-11231. DOI:10.1016/j.ijhydene.2020.07.258
-
[7]肖白, 刘健康, 张博, 等. 考虑阶梯碳交易和需求响应的含氢储能的并网型微电网优化配置[J]. 电力自动化设备, 2023, 43(1): 121-129.
-
[8]孙惠娟, 阙炜新, 彭春华. 考虑电氢耦合和碳交易的电氢能源系统置信间隙鲁棒规划[J]. 电网技术, 2023, 47(11): 4477-4490.
-
[9]李玉婷, 彭敏放. 考虑碳捕集与甲烷化的综合能源微网分布式优化调度[J]. 电力自动化设备, 2023, 43(3): 46-53.
-
[10]陈沼宇, 王丹, 贾宏杰, 等. 考虑P2G多源储能型微网日前最优经济调度策略研究[J]. 中国电机工程学报, 2017, 37(11): 3067-3077.
-
[11]曹继雷. 氢能支撑的风-燃气耦合低碳微网容量优化配置研究[D]. 大连: 大连理工大学, 2021.
-
[12]袁铁江, 曹继雷. 计及风电-负荷不确定性的风氢低碳能源系统容量优化配置[J]. 高电压技术, 2022, 48(6): 2037-2044.
-
[13]FATHY A. A reliable methodology based on mine blast optimization algorithm for optimal sizing of hybrid PVwind-FC system for remote area in Egypt[J]. Renew Energy, 2016, 95: 367-380.
-
[14]杨紫娟, 田雪沁, 吴伟丽, 等. 考虑电解槽组合运行的风电-氢能-HCNG耦合网络容量优化配置[J]. 电力系统自动化, 2023, 47(12): 76-85.
-
[15]张领先, 谢长君, 杨扬, 等. 基于改进混沌粒子群的PEMFC模型参数辨识[J]. 电工电能新技术, 2023, 42(1): 29-39.
-
[16]陈强, 蔡琦盼, 邓博仁. 基于改进混沌粒子群优化算法的永磁同步电机参数辨识[J]. 传感器与微系统, 2023, 42(4): 157-160.
-
[17]ZHOU S, HAN Y, YANG P, et al. An optimal network constraint-based joint expansion planning model for modern distribution networks with multi-types intermittent RERs[J]. Renew Energy, 2022, 194: 137-151.
-
[18]韩莹, 于三川, 李荦一, 等. 计及阶梯式碳交易的风光氢储微电网低碳经济配置方法[J]. 高电压技术, 2022, 48(7): 2523-2533.