|
|
|
发布时间: 2024-06-28 |
特约专栏:韧性配电网 |
|
|
|
收稿日期: 2023-07-13
中图法分类号: TM933
文献标识码: A
文章编号: 2096-8299(2024)03-0214-06
|
摘要
针对配电网户变关系识别不准确而影响配电网正常运作和故障诊断定位的问题,提出了一种基于多元数据驱动的配电网户变关系识别方法。首先,定义了电压的多维波动特征参数指标;其次,采用t分布随机邻域嵌入(t-SNE)算法对电压波动特征矩阵进行降维;然后,利用BIRCH聚类算法对降维后的电压波动特征进行聚类,生成虚拟用户;最后,基于用户功率与上级电表的功率平衡关系假设进行户变关系配对,完成配电网户变关系的识别。案例分析结果表明,相比于之前的户变关系识别方法,所提方法提高了识别准确率。
关键词
配电网; 特征降维; 功率平衡; 户变关系
Abstract
Aiming at the problem of inaccurate identification of user-transformer relationship in distribution networks, which affects the normal operation of distribution networks and fault diagnosis and localisation, a multivariate data-driven user-transformer relationship identification method based on multivariate data is proposed. Firstly, the multidimensional fluctuation characteristic parameter index of voltage is defined, secondly, the t-distributed stochastic neighbourhood embedding (t-SNE) algorithm is used to downscale the voltage fluctuation characteristic matrix, and then the BIRCH clustering algorithm is used to cluster the downsized voltage fluctuation characteristics to form virtual users, and finally, based on the assumption of the user's power balance relationship with the higher-level meter, user-transformer relationship identification is carried out, and user-transformer relationship identification is completed in the distribution network. The results show that compared with the previous identification methods, the identification accuracy is improved.
Key words
distribution network; feature dimension reduction; power balance; usertransformer relationship
配电网运行、负荷扩展、线损改善、故障抢修,乃至停电后电气服务恢复的顺利进行,都离不开配电网低压台区户变关系的准确获取[1-2]。然而,配电网所记录的低压配电台区拓扑结构存在数据缺失、记录错误等问题,只依靠人工方式逐一排查,效率极低,因此户变关系的准确识别成为亟待解决的问题。
近年来,智能表计的应用带动了用电信息采集系统的技术进步,目前数据采集成功率超过了99%[3]。现有的国内外研究方法主要围绕终端通讯和数据驱动两方面。终端通信基于载波通信技术,利用通信物理链路或智能量测通信模块,进行台区内部上下级关系匹配,以完成拓扑识别。数据驱动方法目前研究最为广泛,数据类型多样,侧重点各异,且方法众多。
文献[3-5]针对同台区电压波动相似性假设,提出了基于同相用户量测数据相关性指标和基于聚类的分析方法,但此类方法辨识能力和适应性相对较差。文献[6-10]采用基于同相用户电压波动相似性以及同户表内电压集群特性的聚类方法,完成户变关系的识别。此类方法近年来得到较大发展,如受约束的K-means聚类等,但这类方法在量测数据质量不佳的场合中,辨识能力会受到严重限制。文献[11-12]基于同相用户功率/用电量之和与首端功率/电量基本平衡的假设,将所有用户的相别作为变量,建立了优化模型来求解户变系数。但此类方法无法正确识别长时间处于低功率状态的用户。文献[13]采用了含人工智能方法的降维或精简模型,但此类方法计算复杂度大,且物理原理不够清晰,不利于向电气拓扑识别扩展。
基于上述主流方法的局限性,本文利用智能量测中已有的多元数据,如电压、功率、电流等,提出了一种基于多元数据驱动的配电网户变关系识别方法。首先,针对配电网电压波动的全局特征和局部特征定义相对应的特征参数,对量测电压数据对应的特征参数进行计算,生成高维的电压波动特征矩阵。其次,采用t分布随机领域嵌入(t-distributed Stochastic Neighor Embedding,t-SNE)算法对其进行降维,并采用BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)聚类算法对降维结果进行聚类,以聚类簇为单位生成虚拟用户。然后,使用虚拟用户,来代替包括大量零功率节点在内的原有用户样本,利用最小二乘法进行基于有功功率平衡假设的线性回归,检查每一次回归结果中的异常用户,并对其进行针对性识别,直到全部排除。最后,基于实际案例验证了本文所提方法的有效性。
1 低压台区量测数据分析
1.1 台区电压波动特征分析
1.2 台区有功功率平衡假设
假设同相用户功率之和与首端有功功率基本平衡[14],公式为
| $ P_{\text {trafo }, t}=\sum\limits_{m=1}^M a_m p_{m, t}+e_m $ | (1) |
| $ a_m=\left\{\begin{array}{l} 1, \text { 用户 } m \text { 属于该台区 } \\ 0, \text { 用户 } m \text { 不属于该台区 } \end{array}\right. $ | (2) |
式中:ptrafo,t——t时刻台区低压侧的有功功率;
M——用户m的总数;
am——用户m的有功功率系数;
pm,t——t时刻用户m的有功功率;
em——用户m所属台区的混合偏差,包括量测误差和线路损耗。
由于台区总表的计量精度远高于用户户表[15],计算量测误差时可以假设台区总表的误差无限接近于零。
根据有功功率加和关系方程组,得到用户有功功率系数,判断用户和各台区的对应情况如下:
(1)若用户有功功率系数收敛于1附近,说明该用户有功功率对台区总有功功率有贡献,即该用户属于此台区,本文判定条件为|am-1|≤0.2;
(2)若用户有功功率系数收敛至0附近或远大于1时,可以认为该类用户有功功率与台区总有功功率以及总线损无相关性,不属于本台区,本文判定条件为|am-1| > 0.2。
2 配电网户变关系识别策略
2.1 户变关系识别框架构建
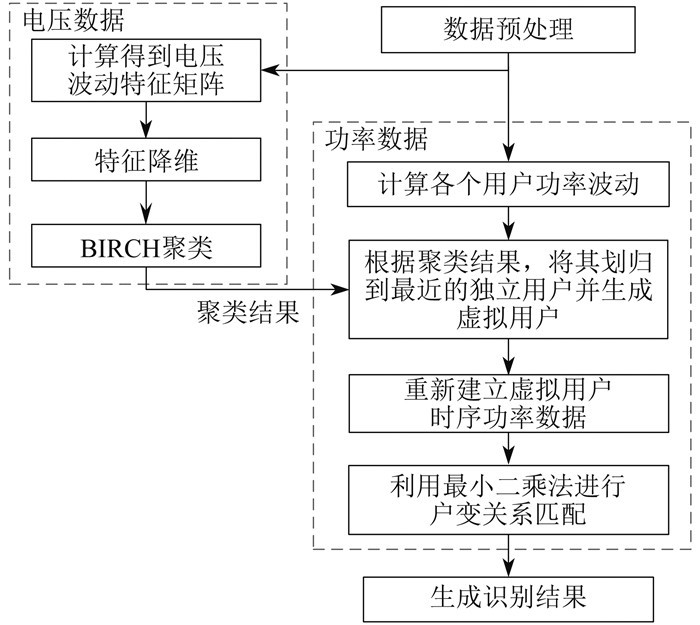
基于低压台区量测数据分析,结合已知的研究方法和实际工程应用,本文提出了一种基于多元数据驱动的配电网户变关系识别方法。具体步骤如下。
(1)数据预处理。获取待识别区域的配变低压侧和用户的电压和功率数据,并根据缺失情况对数据进行适当补充,同时筛选出低功率波动的用户用于对聚类结果的评价。
(2)电压波动特征参数提取。对配电网电压波动的全局特征和局部特征进行表征,对量测电压数据对应的特征参数进行计算,得到电压波动特征矩阵。
(3)特征降维。采用t-SNE算法对电压波动特征矩阵进行降维。
(4)虚拟用户生成。基于降维后的电压波动特征,利用BIRCH聚类算法,对台变电压和用户电压进行聚类,并根据聚类结果,将其划归到最近的独立用户并生成虚拟用户。
(5)虚拟用户-台变关系识别。使用虚拟用户来代替包括大量零功率节点在内的原用户样本,重新建立虚拟用户时序功率数据,利用最小二乘法进行基于有功功率平衡假设的线性回归,对虚拟用户功率数据和台变功率数据进行户变关系匹配,得到识别结果。
依据上述研究思路,构建本文的户变关系识别框架如图 2所示。
2.2 电压波动特征参数提取
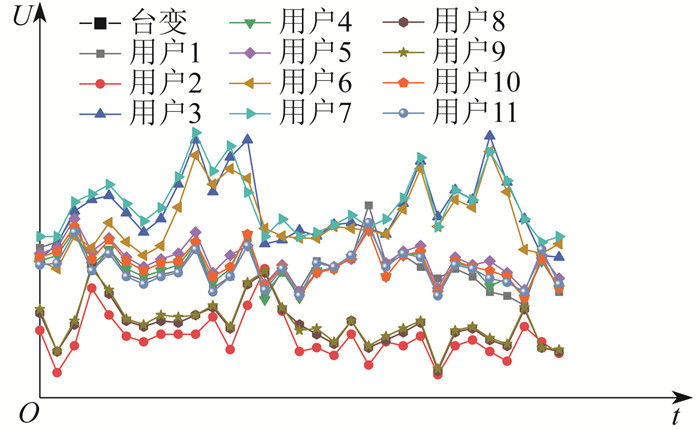
为了区分不同台区的用户,传统方法通过比较各电压曲线的波动相似性进行拓扑识别,例如采用欧氏距离、动态时间弯曲(Dynamic Time Warping,DTW)距离[8],以及导数动态时间弯曲(Derivative Dynamic Time Warping,DDTW)距离[9]等参数,而本文采用电压曲线的多特征参数[1],即电压波动的全局特征和局部特征参数。
设被识别的n个节点(包括用户节点和集中器节点)电压序列分别为U1,U2,U3,…,Ui,…,Un。其中,某一节点i的电压曲线序列为Ui={ui,1,ui,2,ui,3,…ui,j…,ui,T}。T表示电压曲线序列的采样点数,ui,j(j=1,2,3,…,T)表示节点i在时间点j处的电压测量值。针对上述变量,提出电压波动特征参数如下。
(1)电压标准差。反映电压序列Ui的离散程度,用Si表示,公式如下:
| $ S_i=\sqrt{\frac{1}{T} \sum\limits_{j=1}^T\left(u_{i, j}-\mu\right)^2} $ | (3) |
| $ \mu=\frac{1}{T} \sum\limits_{j=1}^T u_{i, j} $ | (4) |
式中:μ——节点i的电压序列的均值。
(2)电压曲线峭度,即电压序列Ui的4阶标准矩。反映电压数据的分布特性,用Ki表示,公式如下:
| $ K_i=\frac{1}{T} \sum\limits_{j=1}^T\left(\frac{u_{i, j}-\mu}{S_i}\right) $ | (5) |
(3)电压曲线偏度,即电压序列Ui的3阶标准矩。反映电压数据分布的偏斜方向及程度,用Ai表示,公式如下:
| $ A_i=\frac{1}{T} \sum\limits_{j=1}^T\left(\frac{u_{i, j}-\mu}{S_i}\right)^3 $ | (6) |
(4)电压曲线斜率。反映电压序列Ui在每一时间点j的电压波动趋势。电压曲线斜率矩阵用Bi表示:
| $ \boldsymbol{B}_i=\left[b_{i, 2}, b_{i, j}, b_{i, T-1}\right], j=2, 3, 4, \cdots, T-1 $ | (7) |
| $ b_{i, j}=\frac{u_{i, j}-u_{i, j-1}}{2}+\frac{u_{i, j+1}-u_{i, j-1}}{4} $ | (8) |
(5)波谷同位置数。波谷位置表示电压波形的极小值点,同时也代表该点电压波形即将升高。因为智能电表通常每15 min采样1次,不同量测之间的对时通常不会超过5 min,所以波谷同位置数可以精细地反映两电压曲线波动起伏的局部相似性。波谷同位置数矩阵用Ni表示:
| $ \begin{aligned} \boldsymbol{N}_i= & {\left[c_{\mathrm{T}}\left(U_i, U_1\right), c_{\mathrm{T}}\left(U_i, U_2\right), \cdots, \right.} \\ & \left.c_{\mathrm{T}}\left(U_i, U_j\right), \cdots, c_{\mathrm{T}}\left(U_i, U_n\right)\right] \end{aligned} $ | (9) |
式中:cT(Ui,Uj)——电压序列Ui、Uj的波峰位置相同点的数目。
(6)波峰同位置数。与波谷位置数相同,通过统计两个电压波形的波峰位置相等数,可得到两电压曲线波动起伏的局部特征。波峰同位置数矩阵用Mi表示:
| $ \begin{aligned} \boldsymbol{M}_i= & {\left[c_{\mathrm{P}}\left(U_i, U_1\right), c_{\mathrm{P}}\left(U_i, U_2\right), \cdots, \right.} \\ & \left.c_{\mathrm{P}}\left(U_i, U_j\right), \cdots, c_{\mathrm{P}}\left(U_i, U_n\right)\right] \end{aligned} $ | (10) |
式中:cP(Ui,Uj)——电压序列Ui、Uj的波峰位置相同点的数目。
因此,对于电压序列Ui,由其电压标准差、电压曲线峭度、电压曲线偏度、电压曲线斜率、波谷同位置数和波峰同位置数等组成的电压波动特征组合参数Ci为
| $ \boldsymbol{C}_i=\left[S_i, K_i, A_i, \boldsymbol{B}_i, \boldsymbol{N}_i, \boldsymbol{M}_i\right] $ | (11) |
对识别区域内所有用户的电压序列进行上述处理,得到它们的特征组合参数,然后,由各电压序列的电压波动特征组合参数构成所有电压序列的电压波动特征矩阵D,可表示为
| $ \boldsymbol{D}=\left[\boldsymbol{C}_1, \boldsymbol{C}_2, \boldsymbol{C}_3, \cdots, \boldsymbol{C}_i, \cdots, \boldsymbol{C}_n\right] $ | (12) |
该矩阵维数为s×n,其中s=2n+(d-2)+3=2n+ d+1,d为每个电压序列的采样点数。由于不同的电压波动特征参数的幅值差异很大,为了避免幅值对参数的影响,需要对其进行归一化,其表达式
| $ \tilde{\boldsymbol{D}}_{p q}=\frac{\boldsymbol{D}_{p q}-\min \left(\boldsymbol{D}_{p k}\right)}{\max \left(\boldsymbol{D}_{p k}\right)-\min \left(\boldsymbol{D}_{p k}\right)} $ | (13) |
其中:p=1,2,3,…,s;q=1,2,3,…,n;k=1,2,3,…,n。
2.3 t-SNE特征降维
通过电压序列构建出的电压波动特征组合参数维度较大,由于指标较多,难免会存在冗余信息。将其直接用于识别流程时,计算复杂度太大。针对上述问题,本文引入t-SNE算法对电压波动特征矩阵进行降维,将s维的电压波动特征组合参数Ci降维为2维的特征参数D_2i=[xi,yi]。
2.4 基于BIRCH聚类算法的虚拟用户生成
利用BIRCH聚类算法对所有用户量测降维后的电压波动特征进行聚类,旨在将数据聚类成一棵树形结构,因此这种算法被称为“层次聚类”。
考虑到低压配电网通常为“配变—表箱—用户”3层次结构,基于电压波动相似性原理,同一层级中波动最大的用户影响着表箱内其他用户的电压波动,同时子层级中所有用户的电压波动也取决于上级设备的电压波动,因此可以通过聚类手段将每一簇视为一个粒度更大的虚拟用户,并将该聚类簇中所有用户每个时间点的功率量测值合并,作为虚拟用户的功率量测值。
2.5 基于最小二乘法的户变关系匹配
线性回归是一种经典的机器学习算法,用于建立输入特征和输出变量之间的线性关系模型。求解该模型的算法有很多,其中最小二乘法计算简单,且鲁棒性较强,是目前应用最广泛的算法之一[16]。该算法通过保证输出值与期望值残差平方和最小,进而对多个输入系数进行拟合。
考虑到上述提到的层次结构和台区有功功率平衡假设,忽略表计及配电设备造成的损耗,流入上级设备的功率、电流必将流到子层级所有用户。理想情况下,只有属于此台区下所有用户的功率加和才会等于此台区表计的功率。因此,可以通过最小二乘法将户变关系识别问题转换为线性关系模型,求出用户有功功率系数,将用户划归到正确的台区。
3 案例分析
3.1 实验数据
3.2 实验过程与分析
由于B村中2#、3#台区的区分难度较高,本文重点以B村为例说明优化的详细过程。
第1步:数据预处理。对获取到的电压和有功功率数据进行分析。
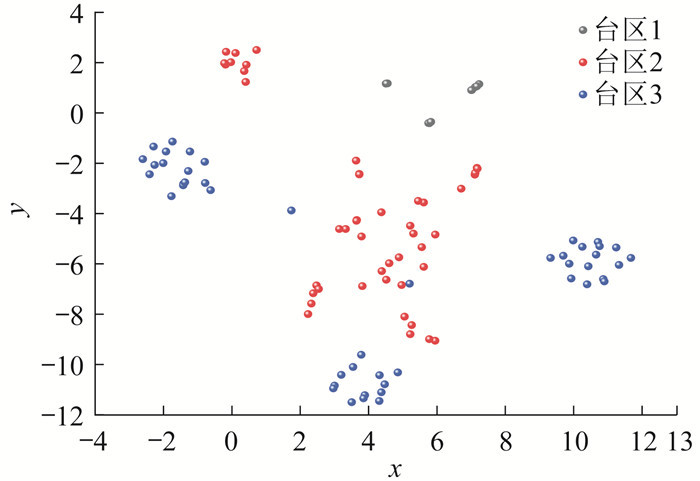
第2步:特征降维。首先根据104个用户的单相电压序列计算得到电压波动特征矩阵 D,再采用t-SNE算法将得到的高维电压波动特征矩阵转化为2维电压波动特征参数矩阵D_2。将2维特征在坐标系下可视化,得到的台区实际用户电压波动特征分布如图 3所示。其中,x、y分别为特征降维后的二维坐标。
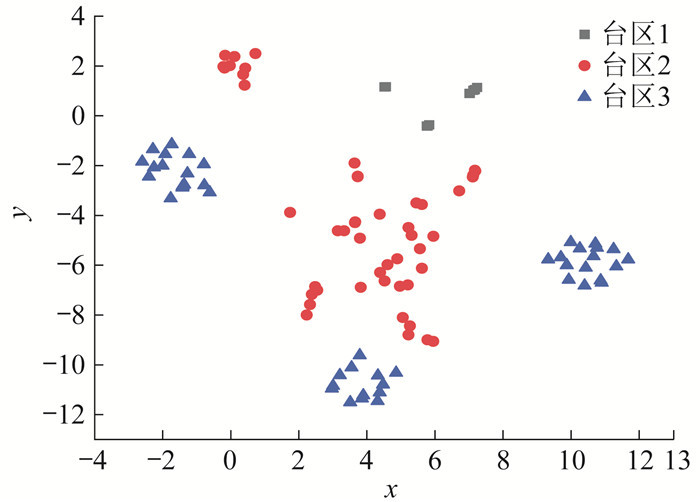
第3步:用户聚类。采用BIRCH聚类算法将降维后的电压特征进行聚类,得到K个聚类簇。由于用户的地理位置信息模糊,故K选择功率波动较大的用户数,并将这些点设置为初始聚类中心进行聚类。聚类后标注的台区用户电压特征分布如图 4所示,其中相同颜色表示同簇用户。
根据图 4中的聚类结果生成虚拟用户,虚拟用户和真实用户关系如表 2所示。
表 2
虚拟用户和真实用户关系
| 虚拟用户 | 包含真实用户 |
| 1 | 0, 1, 3, 4, 7, 8, 9, 10 |
| 2 | 2, 5, 6 |
| 3 | 11, 38, 39, 49, 51 |
| 4 | 12, 37, 41, 50, 52 |
| 5 | 13, 14, 16, 19, 24, 46, 56, 63, 64 |
| 6 | 15, 20, 21, 23, 29, 31, 47, 48 |
| 7 | 17, 35, 36, 40, 42, 43, 44, 45, 54 |
| 8 | 18, 33, 34, 53 |
| 9 | 22, 25, 26, 27, 28, 30, 32, 55 |
| 10 | 57, 61, 65, 66, 74, 76, 80, 82, 86, 90, 95, 98, 102 |
| 11 | 58, 59, 60, 68, 70, 71, 72, 77, 89, 91, 94, 97, 99, 100, 101, 103 |
| 12 | 62, 67, 69, 73, 75, 78, 79, 81, 83, 84, 85, 87, 88, 92, 93, 96 |
第4步:虚拟用户-台变关系识别。虚拟用户时序功率数据采用簇内所有真实用户的功率数据加和。利用最小二乘法对功率数据进行线性回归,可得有功功率系数矩阵。根据识别结果标注的台区用户电压特征分布如图 5所示。
采用同样的数据,本文所提方法(t-SNE+ BIRCH)与其他仅考虑用户单一类型数据特征的主流方法的识别准确率对比如表 3所示。其中,DBSCAN为基于密度的有噪空间聚类应用(Density-Based Spatial Clustering of Application with Noise)算法。
表 3
各种方法的识别准确率对比
| 方法 | 识别准确率/% |
| 电压相关性 | 73.07 |
| 功率线性回归 | 80.76 |
| t-SNE+DBSCAN | 93.56 |
| t-SNE+BIRCH | 98.07 |
由表 3可知,仅基于电压相关性和仅基于功率线性回归的识别方法准确率分别为73.07% 和80.76%,远低于本文所提方法的识别准确率。同时,对于区分难度较高的2#和3#台区,本文所提方法同样实现了较高准确度的辨识。
4 结语
根据电压波动特征和有功功率平衡假设,本文提出了基于多元数据驱动的配电网户变关系识别方法,定义特征参数表征电压波动的全局特征和局部特征,并通过t-SNE算法对电压波动特征矩阵进行降维,根据BIRCH聚类算法的聚类结果生成虚拟用户,引入异常用户检测机制,实现虚拟用户整体识别和异常用户精细识别并行处理,完成整体的户变关系识别。
通过实际案例验证,仅考虑用户单一类型数据特征的户变关系识别方法的识别结果不理想。相较于传统辨识方法,本文构建的拓扑辨识模型的区分度和识别准确率更高。使用虚拟用户来代替包括大量零功率节点在内的用户数据样本,可以极大减小运算的复杂度,降低对算法辨识能力的要求。对实际数据识别时,该模型电压和功率两种类型数据不要求严格同期,整个识别流程不需要新增设备,降低了相关人力物力的投入。本文采用村镇地区作为识别区域,对于规模更大的台区识别,仍有待进一步验证和模型优化。
参考文献
-
[1]崔雪原, 刘晟源, 金伟超, 等. 基于APAA和改进DBSCAN算法的户变关系及相位识别方法[J]. 电网技术, 2021, 45(8): 3034-3043.
-
[2]ZHOU L, WEN F J, YANG X F, et al. User-transformer connectivity relationship identification based on knowledge-driven approaches[J]. IEEE Access, 2022, 10: 54358-54371. DOI:10.1109/ACCESS.2022.3175841
-
[3]夏水斌, 余鹤, 董重重, 等. 基于集抄系统深化应用的低压台区电网拓扑重构方案[J]. 电测与仪表, 2017, 54(20): 110-115.
-
[4]肖勇, 赵云, 涂治东, 等. 基于改进的皮尔逊相关系数的低压配电网拓扑结构校验方法[J]. 电力系统保护与控制, 2019, 47(11): 37-43.
-
[5]黄毕尧, 张明, 李建岐, 等. 联合高低频电力线通信的中压配电网拓扑自动识别方法[J]. 高电压技术, 2021, 47(7): 2350-2358.
-
[6]海迪, 崔娇, 文玉兴, 等. 基于电压波动特征聚类的配电网拓扑识别方法[J]. 湖南师范大学(自然科学学报), 2021, 44(6): 114-120.
-
[7]蔡永智, 唐捷, 阙华坤, 等. 基于电压集群特性分析的台区户变关系校验方法[J]. 广东电力, 2021, 34(8): 50-60.
-
[8]李克明, 江亚群, 黄世付, 等. 基于DTW距离和聚类分析的配电台区低压拓扑结构辨识方法[J]. 电力系统保护与控制, 2021, 49(14): 29-36.
-
[9]刘苏, 黄纯, 侯帅帅, 等. 基于DDTW距离与DBSCAN算法的户变关系识别方法[J]. 电力系统自动化, 2021, 45(18): 71-77.
-
[10]陈招安, 黄纯, 张志丹, 等. 基于T型灰色关联度和KNN算法的低压配电网台区拓扑识别方法[J]. 电力系统保护与控制, 2021, 49(1): 163-169.
-
[11]连子宽, 姚力, 刘晟源, 等. 基于t-SNE降维和BIRCH聚类的单相用户相位及表箱辨识[J]. 电力系统自动化, 2020, 44(8): 176-184.
-
[12]连子宽. 基于数据驱动的低压台区拓扑关系辨识[D]. 杭州: 浙江大学, 2020.
-
[13]冯人海, 赵政, 谢生, 等. 基于主成分分析和凸优化的低压配电网拓扑识别方法[J]. 天津大学学报(自然科学与工程技术版), 2021, 54(7): 746-753.
-
[14]危阜胜, 蔡永智, 唐捷, 等. 基于加权最小二乘法的低压配电台区拓扑自动识别方法[J]. 电力电容器与无功补偿, 2021, 42(5): 122-129.
-
[15]徐焕增, 孔政敏, 王帅, 等. 基于动态线损及FMRLS算法的智能电表误差在线评估模型[J]. 中国电机工程学报, 2021, 41(24): 8349-8358.
-
[16]刘迪, 张强, 吕干云, 等. 基于支路有功功率的配电网拓扑辨识方法[J]. 电力工程技术, 2021, 40(3): 92-98.