|
|
|
发布时间: 2024-06-28 |
特约专栏:韧性配电网 |
|
|
|
收稿日期: 2023-07-14
基金项目: 国家自然科学基金(52007112)
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2024)03-0206-08
|
摘要
提出了一种基于白鲸优化(BWO)算法的配电网故障恢复方法。首先,建立光储、风储系统模型以及负荷模型,以故障后重要负荷损失量最小为目标函数,进行配电网的初步孤岛划分。其次,以网络损耗和开关操作次数加权求和最小为目标,采用BWO算法求解,获取孤岛划分与开关操作配合的故障恢复结果。然后,通过3种场景对比,验证了所提方法能够在不同故障时段获得配电网故障恢复的最优结果。最后,将BWO算法与二进制粒子群优化算法、灰狼优化算法的运行结果进行对比,验证了BWO算法寻优效果更好。
关键词
配电网; 白鲸优化算法; 故障恢复; 孤岛划分; 网络重构; 风光荷时变性
Abstract
A distribution network fault recovery method using the beluga whale optimization (BWO)algorithm is proposed. Firstly, the optical storage and wind storage system models as well as the load model are established. The initial islanding of the distribution network is performed with the objective function of minimizing the amount of important load loss after a fault. Secondly, with the objective of minimizing the weighted sum of network loss and the number of switch operations, the BWO algorithm is used to solve the problem and obtain the fault recovery results of the islanding and switch action cooperation. Thirdly, three scenarios are set up for comparison to verify that the proposed method is able to produce optimal fault recovery results for distribution networks at different fault times. Finally, the results of BWO algorithm are compared with binary particle swarm optimization algorithm and gray wolf optimization algorithm, and the results show that BWO algorithm has better optimization effect.
Key words
distribution networks; beluga whale optimization algorithm; fault recovery; islanding; network reconfiguration; wind and photographic load time variability
近年来,暴雪、冰冻、大雨和高温等极端灾害性天气导致配电网故障频发。在配电网发生故障后,利用分布式电源(Distributed Generation,DG)快速进行负荷供电恢复,对提升配电网抗灾能力具有重大意义。
目前,学者们对配电网故障恢复方法进行了大量的研究。文献[1]提出不仅要恢复重要负荷供电,还要提高负荷恢复总量,通过合理的投切可控负荷,使电源剩余容量在故障发生后得到充分利用。文献[2]通过设立用户停电损失评价指标来解决有源配电网灾后供电恢复问题,实现孤岛数目的优化。文献[3]结合二进制粒子群优化(Binary Particle Swarm Optimization,BPSO)算法与二进制差分进化算法的优势,对故障恢复模型进行求解,取得了较好的恢复效果。文献[4]在进行故障恢复时,建立了考虑DG随时间变化的动态模型。文献[5]考虑了DG对微电网的黑启动能力,同时优化了线路投入顺序。文献[6]先进行孤岛划分恢复重要负荷,然后利用改进灰狼优化(Grey Wolf Optimization,GWO)算法求解重构模型,对剩余负荷进行供电。文献[7]建立双层故障恢复模型,并采用改进蚁群算法进行求解。
上述研究主要关注如何将多种智能算法结合起来[8-12],以进一步发挥各种智能算法的优势,但仍面临收敛速度较慢、计算复杂性较高、易进入局部最优解等问题。此外,在实现故障恢复时,也极少考虑DG输出功率变化和储能装置对孤岛划分的影响[13-15]。针对以上问题,本文在现有研究基础上,引入了白鲸优化(Beluga Whale Optimization,BWO)算法来求解故障恢复模型。在BWO算法中,利用平衡因子和鲸鱼坠落概率的适应性,增强全局搜索和局部搜索能力。此外,加入莱维飞行策略,进一步提高了算法的收敛效率和跳出局部最优解的能力。
1 DG及负荷模型
1.1 DG与储能装置联合系统模型
风机和光伏系统输出功率容易受外界因素影响,波动性大,因此将风机、光伏系统与储能装置组合成联合的风储、光储系统,可以抑制风机、光伏系统输出功率的波动性,使负荷可以稳定运行。单个固定储能装置充放电模型如下:
| $ \left\{\begin{array}{l} \left|P_{\mathrm{B}}(t)\right| \leqslant P_{\max }^{\mathrm{ch}} \\ E(t+1)=E(t)-P_{\mathrm{B}}(t) \leqslant E_{\max } \end{array}\right. $ | (1) |
| $ \left\{\begin{array}{l} P_{\mathrm{B}}(t) \leqslant P_{\max }^{\mathrm{dch}} \\ E(t+1)=E(t)-P_{\mathrm{B}}(t) \geqslant E_{\min } \end{array}\right. $ | (2) |
式中:PB (t)——t时段储能装置输出功率,其值大于零时,为放电状态,反之,为充电状态;
Pmaxch——最大充电功率;
E(t + 1),E(t)——t+1和t时段固定储能装置剩余电量;
Emax——最大剩余电量;
Pmaxdch——最大放电功率;
Emin——最小剩余电量。
风储、光储系统总输出功率P(t)为
| $ P(t)=P_{\mathrm{PV} / \mathrm{WT}}(t)+P_{\mathrm{B}}(t) $ | (3) |
式中:PPV/WT(t)——t时段光伏系统或风机输出功率。
1.2 负荷模型
按用电负荷停电影响安全程度和经济程度将负荷等级分为一级、二级、三级,负荷权重依次为100、10、1。在故障恢复阶段对日负荷曲线函数进行积分计算,可得到节点i的负荷需求Li为
| $ L_i=\int_t^{t+1} f_i(x) \mathrm{d} x, \quad t=1, 2, 3, \cdots, 24 $ | (4) |
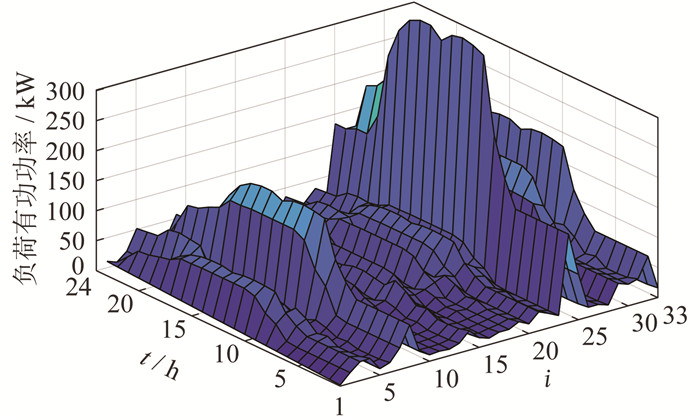
式中:fi(x)——节点i的负荷变化函数,i=1,2,3,…,33。
根据式(4)计算,得到的一日内负荷有功功率时变图如图 1所示。
2 孤岛划分策略
2.1 孤岛划分目标函数
孤岛划分以故障后重要负荷损失量f1最小为目标,建立目标函数如下:
| $ \max f_1=\sum\limits_{t=1}^T \sum\limits_{i=1}^N\left(\omega_i \delta_{i, t} P_{i, t}^{\text {Load }}\right) $ | (5) |
式中:T——总故障停电时间;
N——配电网中所有节点总数;
ωi——节点i的负荷权重;
δi,t——0-1变量,表示负荷投入和切除状态,如果节点i在t时段被切除,取值为1,反之,取值为0;
Pi,tLoad——t时段节点i的负荷功率。
2.2 孤岛划分约束条件
孤岛功率平衡方程约束条件为
| $ P_{i, t}=U_{i, t} \sum\limits_{j=1}^N U_{j, t}\left(G_{i j} \cos \theta_{i j, t}+B_{i j} \sin \theta_{i j, t}\right) $ | (6) |
| $ Q_{i, t}=U_{i, t} \sum\limits_{j=1}^N U_{j, t}\left(G_{i j} \sin \theta_{i j, t}-B_{i j} \cos \theta_{i j, t}\right) $ | (7) |
式中:Pi,t,Qi,t——t时段节点i的有功功率、无功功率;
Ui,t,Uj,t——t时段节点i和j的电压幅值;
Gij,Bij——支路i-j的电导、电纳;
θij,t——t时段支路i-j的相角差。节点电压约束条件为
| $ U_i^{\min } \leqslant U_{i, t} \leqslant U_i^{\max } $ | (8) |
式中:Uimin,Uimax——节点i的电压幅值下限和上限。支路电流约束条件为
| $ I_{i j, t} \leqslant I_{i j}^{\max } $ | (9) |
式中:Iij,t——t时段支路i-j的电流值;
Iijmax——支路i-j最大允许的电流值。
DG功率约束条件为
| $ P_{i, t}^{\mathrm{DG}}=\hat{P}_{i, t}^{\mathrm{DG}} $ | (10) |
| $ Q_{i, t}^{\mathrm{DG}}=P_{i, t}^{\mathrm{DG}} \tan \theta_i^{\mathrm{DG}} $ | (11) |
| $ \sqrt{\left(P_{i, t}^{\mathrm{DG}}\right)^2+\left(Q_{i, t}^{\mathrm{DG}}\right)^2} \leqslant S_i^{\mathrm{DG}} $ | (12) |
式中:Pi,tDG——t时段节点i处DG有功功率;
Qi,tDG——t时段节点i处DG无功功率;
θiDG——t时段节点i处DG功率因数角;
SiDG——节点i处DG的容量。
辐射状运行结构约束条件为
| $ g \in G $ | (13) |
式中:g——孤岛划分后的配电网拓扑结构;
G——配电网辐射状运行所满足的结构集合。
2.3 孤岛划分策略流程
孤岛划分策略具体步骤如下。
(1)确定故障后DG输出有功功率以及失电负荷等级。
(2)以DG布置节点为搜索起点,利用广度优先搜索算法,以故障时段DG输出的有功功率为范围进行搜索。若出现孤岛交叉情况,则进行孤岛融合。
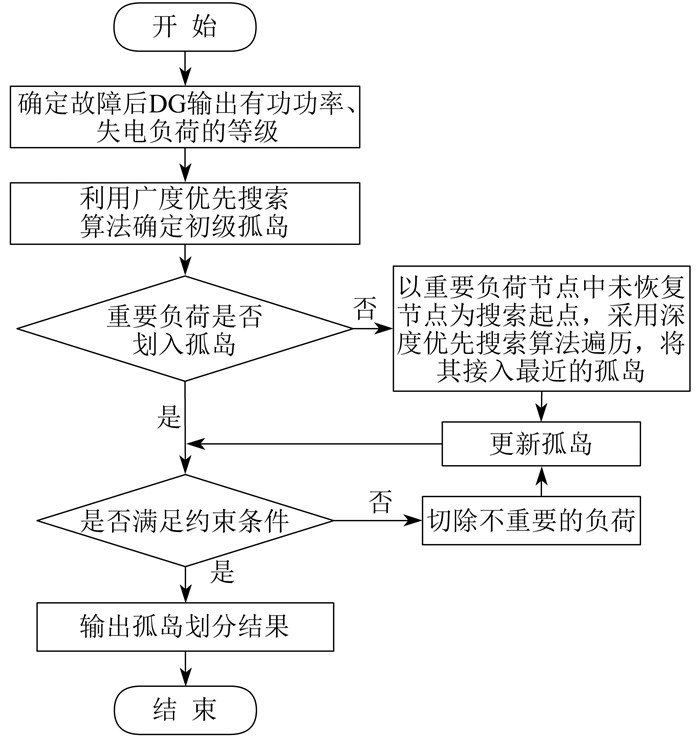
(3)以重要负荷节点中未恢复节点为搜索起点,采用深度优先搜索算法遍历,将其划入电气距离最近的孤岛,验证是否满足孤岛划分约束条件。如果不满足约束条件,根据孤岛内负荷重要性,切除不重要的负荷,直到满足约束条件,得出孤岛划分结果。孤岛划分策略流程如图 2所示。
3 基于BWO算法的配电网故障恢复重构策略
3.1 配电网故障恢复模型
以网络损耗和开关操作次数加权求和f最小为目标,建立目标函数如下:
| $ \min f=a_1 \sum\limits_{l=1}^L \varphi_l Z_l \frac{P_l^2+Q_l^2}{U_l^2}+a_2 \sum\limits_{c=1}^c\left|\lambda_c^t-\lambda_c^{t+1}\right| $ | (14) |
式中:a1,a2——赋权值,着重考虑网络损耗并兼顾开关次数,a1取0.7,a2取0.3;
l,L——支路编号和支路总数;
φl——0-1变量,表示支路l的开合状态,如果支路l闭合,取值为1,反之,取值为0;
Zl——支路l的阻抗;
Pl——支路l末尾节点的有功功率;
Ql——支路l末尾节点的无功功率;
Ul——支路l末尾节点的电压幅值;
c,C——开关编号和开关总数;
λct——0-1变量,表示第t时段开关c的开合1,反状态,如果开关c闭合,取值为之,取值为0。
故障恢复约束条件与式(6)至式(13)相同。
3.2 BWO算法
BWO算法包含搜索、捕食、鲸鱼坠落3个阶段。
白鲸种群位置X可描述为
| $ \boldsymbol{X}=\left[\begin{array}{cccc} x_{1, 1} & x_{1, 2} & \cdots & x_{1, d} \\ x_{2, 1} & x_{2, 2} & \cdots & x_{2, d} \\ \vdots & \vdots & & \vdots \\ x_{n, 1} & x_{n, 2} & \cdots & x_{n, d} \end{array}\right] $ | (15) |
式中:n——白鲸种群数量;
d——白鲸种群维数。
对应的白鲸种群适应度F公式如下:
| $ \boldsymbol{F}=\left[\begin{array}{c} f\left(x_{1, 1}, x_{1, 2}, \cdots, x_{1, d}\right) \\ f\left(x_{2, 1}, x_{2, 2}, \cdots, x_{2, d}\right) \\ \vdots \\ f\left(x_{n, 1}, x_{n, 2}, \cdots, x_{n, d}\right) \end{array}\right] $ | (16) |
式中:f(·)——式(14)中的目标函数。
BWO算法从搜索阶段转换到捕食阶段,由平衡因子Bf控制,其定义为
| $ B_{\mathrm{f}}=B_0\left(1-\frac{I}{2 I_{\max }}\right) $ | (17) |
式中:B0——(0,1)之间的随机数;
I——当前迭代次数;
Imax——最大迭代次数。
(1)搜索阶段 该阶段白鲸的位置由白鲸的配对游泳行为来更新,根据从d维中选择的随机整数q(q=1,2,3,…,d)的奇偶性采用不同公式更新白鲸的位置。
q为偶数时,有
| $ x_{p, q}^{I+1}=x_{p, q}^I+\left(x_{r, 1}^I-x_{p, q}^I\right)\left(1+r_1\right) \sin \left(2 {\rm{ \mathsf{ π} }} r_2\right) $ | (18) |
q为奇数时,有
| $ x_{p, q}^{I+1}=x_{p, q}^I+\left(x_{r, 1}^I-x_{p, q}^I\right)\left(1+r_1\right) \cos \left(2 {\rm{ \mathsf{ π} }} r_2\right) $ | (19) |
式中:xp,qI+1,xp,qI——第p只白鲸在第q维度上的新位置和当前位置;
xr,1I——随机选择的第r条白鲸在第1维度上的位置;
r1,r2——用于增强搜索阶段的随机算子,(0,1)之间的随机数。
(2)捕食阶段 该阶段引入莱维飞行策略以增强收敛能力。其数学模型为
| $ \boldsymbol{X}_p^{I+1}=r_3 \boldsymbol{X}_{\text {best }}^I-r_4 \boldsymbol{X}_p^I+C_1 L_{\mathrm{F}}\left(\boldsymbol{X}_r^I-\boldsymbol{X}_p^I\right) $ | (20) |
式中:XpI+1——第p条白鲸的新位置;
r3,r4——(0,1)之间的随机数;
XbestI——白鲸种群中的最好位置;
XpI——第p条白鲸的当前位置;
C1——莱维飞行的随机跳跃强度;
LF——莱维飞行函数;
XrI——随机选择的第r条白鲸的当前位置。
其中:
| $ L_{\mathrm{F}}=0.05 \times \frac{u \sigma}{|v|^{1 / \beta}} $ | (21) |
| $ \sigma=\left\{\frac{\Gamma(1+\beta) \sin ({\rm{ \mathsf{ π} }} \beta / 2)}{\Gamma[(1+\beta) / 2] \beta \times 2^{(\beta-1) / 2}}\right\}^{1 / \beta} $ | (22) |
式中:u,v——正态分布随机数;
σ——莱维飞行函数中的参数;
β——常数,取1.5;
Γ(·)——伽玛函数。
(3)鲸鱼坠落阶段 该阶段利用白鲸的位置和鲸鱼落体的步长来更新位置,以保证种群大小的恒定,其数学模型为
| $ \boldsymbol{X}_p^{I+1}=r_5 \boldsymbol{X}_p^I-r_6 \boldsymbol{X}_r^I+r_7 \boldsymbol{X}_{\text {step }} $ | (23) |
式中:r5,r6,r7——(0,1)之间的随机数;
Xstep——鲸鱼坠落的步长。
其中:
| $ \boldsymbol{X}_{\text {step }}=\left(\boldsymbol{u}_{\mathrm{b}}-\boldsymbol{l}_{\mathrm{b}}\right) \exp \left(-C_2 \frac{I}{I_{\text {max }}}\right) $ | (24) |
| $ C_2=2 W_{\mathrm{f}} n $ | (25) |
| $ W_{\mathrm{f}}=0.1-0.05 \frac{I}{I_{\max }} $ | (26) |
式中:ub,lb——搜索边界上下限;
C2——阶跃因子;
Wf——鲸鱼坠落概率。
在BWO算法中对白鲸位置的更新是持续性的,而故障恢复问题中开关的状态只有打开和闭合两种情况。对更新后白鲸的位置进行离散化处理,公式如下:
| $ x_{p, q}^I= \begin{cases}0, & r_{\text {and }}>S\left(x_{p, q}^I\right) \\ 1, & r_{\text {and }} \leqslant S\left(x_{p, q}^I\right)\end{cases} $ | (27) |
| $ S\left(x_{p, q}^I\right)=\frac{1}{1+\exp \left(x_{p, q}^I\right)} $ | (28) |
式中:rand——[0, 1]范围内的随机数;
S(x)——S型离散函数。
3.3 基于BWO算法的配电网故障恢复重构策略流程
配电网故障恢复重构策略具体步骤如下。
(1)当配电网发生故障后,先将故障支路隔开,然后划分为若干孤岛,并更新孤岛划分后的配电网具体参数。
(2)确定配电网中剩余失电负荷和可利用开关状态信息。
(3)设置BWO算法相关的参数:白鲸种群数量、白鲸种群维数、最大迭代次数。
(4)初始化白鲸种群位置,各白鲸初始位置随机产生,并根据式(16)计算得到对应的白鲸种群适应度值。
(5)根据式(17)和式(26)计算得到平衡因子Bf,鲸鱼坠落概率Wf。
(6)所处阶段不同的白鲸位置更新公式不同,根据计算得到的平衡因子Bf的值决定白鲸所处阶段。若Bf > 0.5,白鲸处于搜索阶段,由式(18)、式(19)更新白鲸的位置;若Bf ≤0.5,白鲸处于捕食阶段,由式(20)更新白鲸的位置。将新位置值代入式(16)求得当前适应度值,并进行比较排序,得出当前迭代情况下最优解。
(7)计算鲸鱼坠落概率Wf,比较其与平衡因子Bf的大小,若Wf > Bf,根据式(23)更新白鲸位置。
(8)判断当前迭代次数与最大迭代次数的关系。如果当前迭代次数达到最大迭代次数,则停止搜索并输出最优参数和故障恢复结果;反之,返回(5)继续新一轮的寻优搜索。
基于BWO算法的配电网故障恢复重构策略流程如图 3所示。
4 算例分析
4.1 算例参数
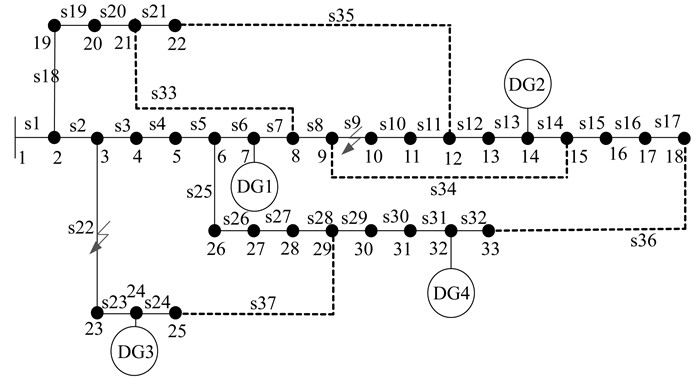
本文以IEEE 33节点配电网系统为例,系统结构如图 4所示。其中,1~33为负荷节点,s1~s37为节点间线路,DG1、DG2为光储系统,DG3、DG4为风储系统。
节点负荷等级及权重如表 1所示。
表 1
节点负荷等级及权重
| 负荷等级 | 负荷节点 | 负荷权重值 |
| 一级 | 7、14、16、24、31 | 100 |
| 二级 | 2、6、8、21、29、32 | 10 |
| 三级 | 其他 | 1 |
假设由于极端灾害导致线路s9、s22发生断线故障。设置发生上述故障的两个时段,分别为12:00—13:00(时段1)和18:00—19:00(时段2)。DG1~DG4在两个故障时段的DG参数如表 2所示。
表 2
DG参数
| 电源 | 接入节点 | 时段1输出有功功率/kW | 时段2输出有功功率/kW | 储能最大功率/kW |
| DG1 | 7 | 800 | 700 | 150 |
| DG2 | 14 | 650 | 500 | 250 |
| DG3 | 24 | 400 | 750 | 200 |
| DG4 | 32 | 350 | 700 | 150 |
先进行初步孤岛划分,然后,对配电网中剩余可利用的开关进行编码,采用BWO算法求解重构模型,设置白鲸种群数量为20,白鲸种群维数为37,最大迭代次数为50次。
4.2 算例结果分析
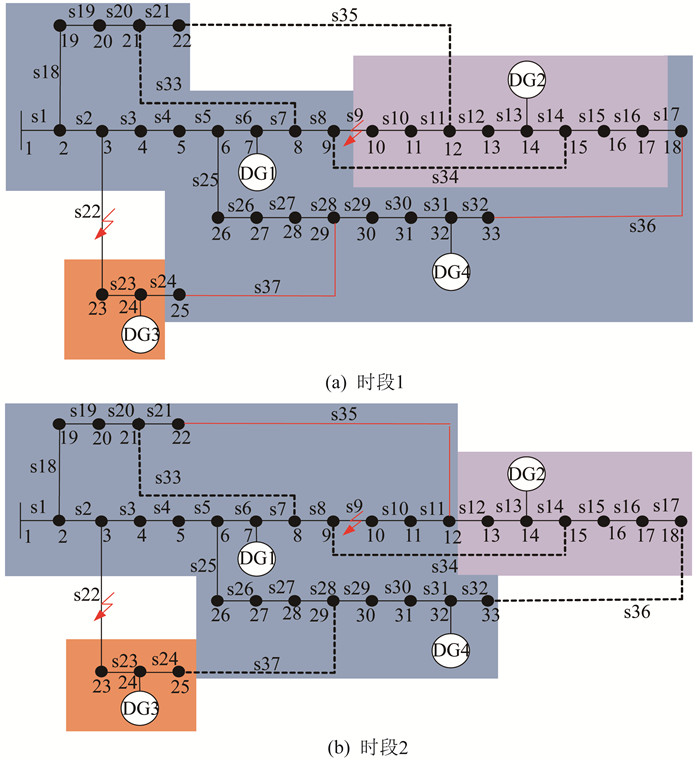
孤岛划分和孤岛划分与基于BWO算法的故障恢复重构策略配合(以下简称“孤岛划分+重构”)的两种故障恢复方法的结果对比如表 3所示。采用孤岛划分+重构方法时,两个故障时段的故障恢复结果如图 5所示。
表 3
两种故障恢复方法的结果对比
| 故障时段 | 策略 | 网络损耗/kW | 开关操作次数/次 | 节点电压幅值最小值(p.u.) |
| 12:00—13:00(时段1) | 孤岛划分 | 110.34 | 0.947 5 | |
| 孤岛划分+重构 | 92.80 | 2 | 0.956 1 | |
| 18:00—19:00(时段2) | 孤岛划分 | 127.56 | 0.936 7 | |
| 孤岛划分+重构 | 108.26 | 1 | 0.925 6 |
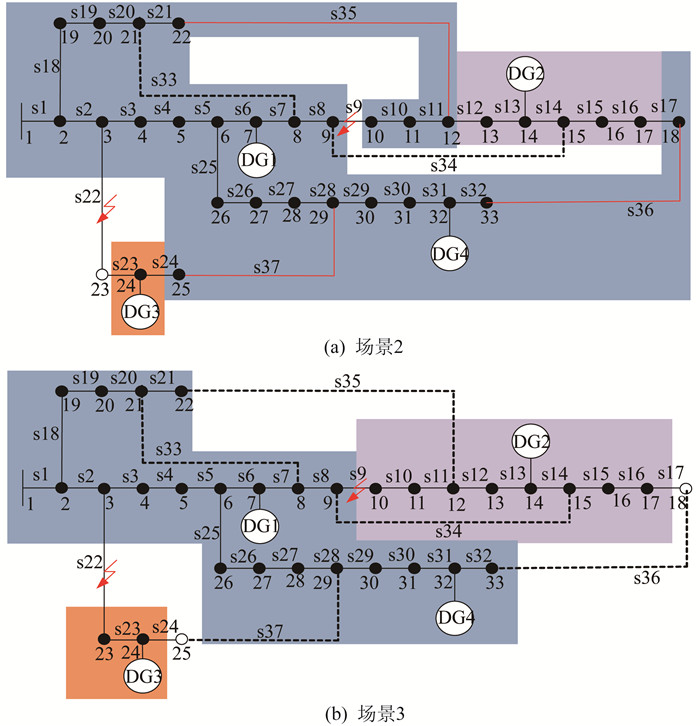
由表 3可知,同一故障时段,孤岛划分+重构的故障恢复方法所得到的网络损耗较仅进行孤岛划分的故障恢复方法小,但节点最小电压较仅进行孤岛划分的故障恢复方法有所提升,说明采用孤岛划分+重构的故障恢复方法效果更好。由图 5分析可知:由于负荷需求和风储、光储系统输出有功功率不同,两个故障时段开关操作次数不同。在时段1,由于DG2光储系统输出有功功率较多,被纳入岛内负荷较多,线路s36闭合联络开关将负荷节点18并入主网,由于DG3风储系统输出有功功率不足,线路s37闭合联络开关将较大的负荷节点25并入主网中。在时段2,由于DG2光储系统输出有功功率不足,孤岛较故障时段1有很大的调整,负荷节点13、14、15、16、17、18与DG2构成孤岛,线路s35闭合联络开关将负荷节点10、11、12并入主网恢复供电,由于DG3风储系统输出有功功率增加,将负荷节点25纳入孤岛中,负荷节点23、24、25与DG3构成孤岛。
为了进一步验证本文中所提孤岛划分+重构的故障恢复方法的有效性。假设发生同一故障,对时段1设置3种场景进行分析。场景1:考虑风光荷的不确定性,采用上述孤岛划分+重构的模型恢复配电网故障。场景2:采用上述孤岛划分+ 重构的模型进行故障恢复,但DG1~DG4不接入储能装置构成光储、风储系统。场景3:不用基于BWO算法的故障恢复重构策略恢复供电剩余的失电区域,只对配电网进行孤岛划分。场景1的故障恢复结果如图 5(a)所示,场景2、场景3的故障恢复结果如图 6所示,不同场景的故障恢复结果对比如表 4所示。
表 4
不同场景的故障恢复结果对比
| 场景 | 负荷恢复量/kW | 开关操作次数/次 | 网络损耗/kW | 节点电压幅值最小值(p.u.) | 失电负荷节点 | |
| 孤岛 | 主网 | |||||
| 1 | 1 035 | 1 751 | 2 | 92.80 | 0.956 1 | |
| 2 | 450 | 2 269 | 3 | 88.01 | 0.958 3 | 23 |
| 3 | 1 035 | 1 628 | 110.34 | 0.929 5 | 18、25 | |
由表 4可知:场景1能恢复所有失电负荷节点;场景2网络损耗比场景1稍低,由于没有储能装置,场景2孤岛划分范围较小,孤岛内负荷恢复量少,导致负荷节点23失电;场景3中未对配电网进行恢复重构,没有闭合联络开关,造成主网负荷恢复量少,导致负荷节点18、25失电。这说明场景1(即本文所提方法)的故障恢复结果优于场景2、场景3,获得配电网故障恢复的最优结果,不仅恢复了全部失电负荷,而且降低了网络损耗。
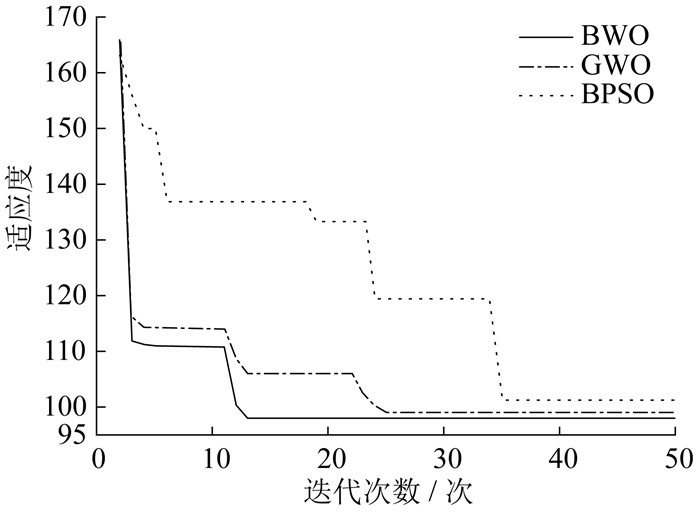
为了验证BWO算法的性能,参数设置不变,分别采用BWO算法、GWO算法以及BPSO算法进行故障恢复,不同算法故障恢复迭代效果对比如图 7所示。然后,分别计算各算法运行50次的结果平均值。不同算法故障恢复性能对比如表 5所示。
表 5
不同算法故障恢复性能对比
| 算法 | 陷入局部最优次数/次 | 平均求解时间/s | 平均迭代次数/次 |
| BWO | 1 | 7.36 | 12.8 |
| GWO | 2 | 14.35 | 25.1 |
| BPSO | 4 | 15.61 | 35.3 |
由图 7可知,BWO算法适应度的最终值明显低于GWO和BPSO算法,这表明BWO算法具有良好的全局收敛能力,可以有效地避免陷入局部最优。由表 5可知:BWO算法获得最优解的平均迭代次数只需要12.8次,比GWO和BPSO算法都要少很多,说明BWO算法能够有效地平衡全局搜索和局部开发的能力,从而大大加快了收敛的速度;在平均求解时间方面,BWO算法平均耗时也最少,且陷入局部最优解次数最少。
5 结语
本文提出了孤岛划分+重构的故障恢复方法。在孤岛划分阶段,以故障后重要负荷损失量最小为目标,利用广度优先搜索算法和深度优先搜索算法相结合进行计算,结果表明能够快速对故障后的配电网进行孤岛划分,保证DG优先恢复重要负荷供电。在重构阶段,以网络损耗和开关操作次数加权求和最小为目标,利用BWO算法进行寻优计算。算例结果表明,本文所提方法可获得配电网故障恢复最优结果,不仅恢复了全部失电负荷,而且降低了网络损耗。将BWO算法与GWO算法、BPSO算法的运行结果进行对比,结果表明BWO算法能避免陷入局部最优解且求解速度最快,验证了BWO算法的寻优效果更好。
参考文献
-
[1]杨丽君, 张广超, 吕雪姣, 等. 考虑可控负荷的含分布式电源配电网短时故障供电恢复[J]. 电力自动化设备, 2016, 36(11): 11-17.
-
[2]闫涵, 王建华, 范须露, 等. 基于用户停电损失评估的有源配电网灾后供电恢复模型[J]. 电力系统自动化, 2022, 46(5): 31-42.
-
[3]周湶, 解慧力, 郑柏林, 等. 基于混合算法的配电网故障重构与孤岛运行配合[J]. 电网技术, 2015, 39(1): 136-142.
-
[4]齐郑, 张首魁, 李志, 等. 考虑时间尺度的含DG配电网故障动态恢复策略[J]. 电力系统保护与控制, 2017, 45(16): 31-38.
-
[5]杨智豪, 牟龙华, 刘仲, 等. 微电网黑启动中考虑DG特性与线路投入顺序的串行恢复策略[J]. 电力系统保护与控制, 2016, 44(18): 17-23.
-
[6]王红君, 陈智晴, 赵辉, 等. 考虑风光荷不确定性的配电网故障恢复策略[J]. 电网技术, 2022, 46(11): 4356-4364.
-
[7]杨丽君, 王晨, 赵优, 等. 基于双层优化模型的电-气耦合综合能源故障恢复策略[J]. 电网技术, 2020, 44(11): 4264-4273.
-
[8]马天祥, 王春英, 贾静然, 等. 基于二进制粒子群算法的交直流混合配电网故障恢复方法[J]. 电力系统保护与控制, 2019, 47(9): 112-119.
-
[9]徐岩, 张荟, 马天祥, 等. 含分布式电源的配电网故障紧急恢复与抢修协调优化策略[J]. 电力系统自动化, 2021, 45(22): 38-46.
-
[10]陈春, 吴宜桐, 李锰, 等. 基于网络拓扑有向遍历的配电网故障快速恢复方法[J]. 电力系统自动化, 2021, 45(7): 44-52.
-
[11]李丝雨, 张彼德, 彭丽维, 等. 考虑柔性负荷调节能力的主动配电网动态孤岛划分策略[J]. 高电压技术, 2019, 45(6): 1835-1842.
-
[12]胡哲晟, 郭瑞鹏, 蓝海波, 等. 基于有向图的含分布式电源配电网孤岛划分模型[J]. 电力系统自动化, 2015, 39(14): 97-104.
-
[13]王雨婷, 张筱慧, 唐巍, 等. 考虑光伏及负荷时变性的配电网故障恢复[J]. 电网技术, 2016, 40(9): 2706-2716.
-
[14]杨丽君, 高鹏, 王伟浩, 等. 考虑时间尺度的配电网故障恢复方法研究[J]. 太阳能学报, 2021, 42(1): 453-459.
-
[15]李振坤, 周伟杰, 王坚敏, 等. 基于风光荷功率曲线的有源配电网动态孤岛划分方法[J]. 电力系统自动化, 2016, 40(14): 58-64.