|
|
|
发布时间: 2024-06-28 |
特约专栏:韧性配电网 |
|
|
|
收稿日期: 2024-03-08
基金项目: 国家自然科学基金(61873159);上海市自然科学基金(22ZR14255)
中图法分类号: TM732
文献标识码: A
文章编号: 2096-8299(2024)03-0198-08
|
摘要
针对极端灾害会导致配电网线路断开和负荷失电等问题,提出了以智能软开关与移动储能作为灵活性资源的两阶段配电网韧性提升策略。首先,建立配电-交通耦合网络和灾前两阶段鲁棒优化模型,进行最恶劣光伏功率输出场景下移动储能的灾前部署,求解得到移动储能位置与数量部署方案。然后,基于灾前部署方案,建立多源协同的配电网灾后故障恢复混合二阶锥规划模型,进而考虑智能软开关、移动储能的优化调度及电动汽车充放电,求解得到最优灾后故障恢复方案。最后,通过算例分析验证了该策略的有效性。
关键词
智能软开关; 移动储能; 灾前鲁棒优化; 灾后故障恢复; 韧性配电网
Abstract
In view of the problems that extreme disasters can cause distribution network lines to be disconnected and loads to lose power, a two-stage distribution network resilience improvement strategy considering mobile energy storage and soft open point as flexible resources is proposed. First, a two-stage pre-disaster robust optimization model is built under the power distribution-traffic coupling network, and pre-disaster deployment of mobile energy storage under the worst photovoltaic output scenario is carried out, and the location and quantity deployment plan of mobile energy storage is obtained. Then, based on the pre-disaster deployment plan, a multisource coordinated post-disaster fault recovery hybrid second-order cone programming model is established, and then the optimal dispatch of soft open point, mobile energy storage, and electric vehicle charging and discharging are taken into consideration to obtain the optimal post-disaster fault recovery. The scheme and numerical example analysis verify the effectiveness of this strategy.
Key words
intelligent soft open point; mobile energy storage; pre-disaster robust optimization; post-disaster recovery; resilient distribution network
近年来,极端灾害频繁发生,配电网作为电力系统的重要枢纽,一旦发生瘫痪,势必造成巨大的社会经济损失与不良影响。配电网韧性指系统抵御极端灾害破坏,吸收、适应并于事后快速恢复的能力[1]。在灾害发生前后,合理利用配电网内的灵活性资源对增强配电网韧性至关重要。分布式电源(Distributed Generation,DG)可以作为应急资源参与灾后供电恢复。文献[2]考虑了含DG配电网的灾中、灾后两阶段协同的韧性恢复决策。文献[3-6]提出了含DG的配电网故障恢复方案,发现当配电网发生故障时,上级电网供电范围减小,用以恢复供电的DG由于不具备电压控制能力,大多退出运行,而智能软开关(Soft Open Point,SOP)作为取代传统联络开关的电力电子设备,具有控制潮流、调控电压的作用。文献[7]提出了SOP和DG协同的故障恢复策略,并采用混沌蚁群混合算法求解。文献[8]提出了含SOP的两阶段故障恢复方法。文献[9]提出了SOP控制模型与含SOP的配电网供电恢复模型。
作为移动资源,移动储能车(Mobile Energy Storage Vehicle,MESV)可提高配电网在极端灾害下的韧性。文献[10]建立了考虑恢复力与经济性均衡的MESV灾前配置策略。文献[11]建立了可再生能源配电网的多目标优化运行模型,以实现MESV位置、充放电状态,以及不同时段电量的优化决策。文献[12]提出了地震灾害下含MESV的配电网韧性提升方法,但没有考虑灾后MESV的移动调度。文献[13]建立了MESV灾前配置与灾后调度的两阶段模型,以增加配电网韧性。文献[14]提出了台风场景下基于多种分布式资源协同的配电网两阶段供电恢复策略,但无法解决恢复过程中DG由于电压不足退出运行的问题。
基于以上分析,本文提出了含SOP与MESV的两阶段配电网韧性提升方法。首先,在灾前阶段,考虑光伏输出功率的不确定性与配电网重构,以负荷削减成本和MESV配置成本最低为目标函数,建立灾前鲁棒优化模型,求解得到最恶劣光伏输出功率下的MESV灾前部署方案。其次,在灾后阶段,考虑SOP的接入、MESV的灾后调度及DG与电动汽车等分布式资源的协同,进行多源协同故障恢复,以最小化负荷削减成本。最后,通过IEEE 33节点算例,验证所提方法的有效性。
1 含SOP与MESV的两阶段配电网韧性提升策略
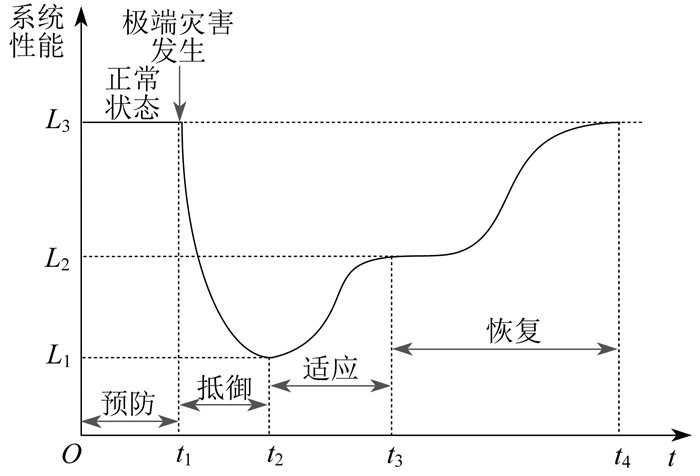
极端灾害下配电网性能曲线如图 1所示[15]。其中,t1为极端灾害开始时刻,t2为极端灾害对电网影响最大时刻,t3为电网开始恢复时刻,t4为电网恢复阶段结束时刻。L1、L2、L3为3种性能。
由图 1可知,极端灾害下配电网4个阶段分别为:预防阶段(0~t1);抵御阶段(t1~t2);适应阶段(t2~t3);恢复阶段(t3~t4)。
本文针对预防阶段和恢复阶段,分别给出不同的韧性提升策略。预防阶段:在灾害发生时刻与持续时间未知的前提下,对MESV的数量与位置进行部署,考虑光伏极端输出功率场景与网络重构,确保MESV在灾害发生后快速响应并参与负荷恢复;恢复阶段:建立多源协同的灾后故障恢复模型,通过调度MESV、智能软开关、电动汽车等资源,实现电能在时空上的优化分配,尽可能对重要负荷恢复供电,提升极端灾害下两阶段的配电网韧性。
1.1 SOP主要功能
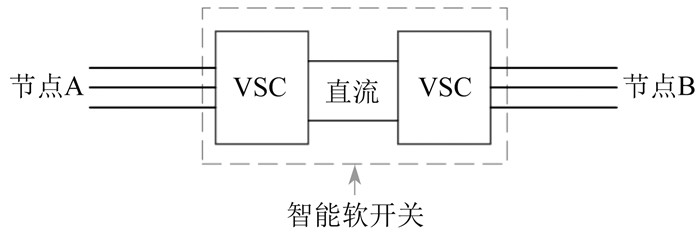
适用于SOP的电力电子装置主要有以下3种:背靠背电压源型换流器(Back-to-Back Voltage Source Converter,B2B VSC)、静止同步串联补偿器和统一潮流控制器。这里以B2B VSC为例,其基本结构由一个直流电容器和两个换流器(Voltage Source Converter,VSC)组成。B2B VSC结构如图 2所示。
相较于传统联络开关,SOP可以实现功率的连续调节与控制,改善系统功率分布,减少运行损耗;可以为两端馈线提供无功补偿,确保电能质量与电压稳定;响应时间短,不依赖机械操作,且开关损耗低;故障时可以恢复失电负荷。因此,本文将SOP应用于配电网的故障恢复过程。
VSC的控制模式可根据不同系统运行状况改变。B2B VSC的4种典型控制模式和适用场景如表 1所示。
表 1
B2B VSC的控制模式和适用场景
| 控制模式 | VSC1 | VSC2 | 适用场景 |
| 1 | PQ控制 | UdcQ控制 | 正常运行 |
| 2 | UdcQ控制 | PQ控制 | 正常运行 |
| 3 | Uf控制 | UdcQ控制 | VSC1侧故障 |
| 4 | UdcQ控制 | Uf控制 | VSC2侧故障 |
正常运行状态下,一侧VSC进行功率控制,另一侧VSC进行直流电压控制,当某一侧线路发生故障时,对应的一侧VSC切换为电压频率控制,对该侧进行负荷电压支撑,维持电压频率稳定。由于SOP控制模式的切换时间短于联络开关的动作时间,因而可以实现非故障区域不间断供电。考虑到短路电流容量、电磁环网等因素的影响,配电网通常采取闭环设计、开环运行的方式,因而无法进一步提升供电可靠性。智能软开关等柔性设备的接入,使配电网具有了柔性闭环的能力,不仅带来了更高的供电可靠性,而且能够解决因大量DG与直流负荷接入配电网引起的电压波动问题。
1.2 MESV时空调度
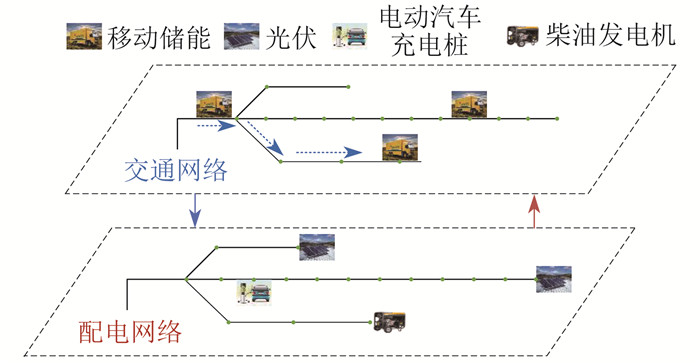
配电-交通耦合网络结构如图 3所示。
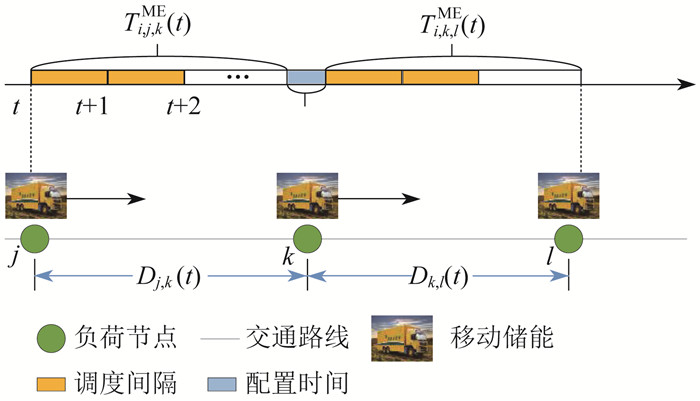
MESV调度可看作一个路径问题[16]。MESV调度状态由其充放电状态和行驶状态共同决定,不仅受自身状态、时间与空间的影响,还受到交通网络中实时路况、突发事件的影响。极端灾害发生后,MESV从车辆中心转移到失电节点,以支持重要负荷;当相邻负荷恢复后,MESV前往其他节点支持对应负荷。MESV时空调度过程如图 4所示。其中,Ti,j,kME (t)为第i个MESV从节点j到节点k的行驶时间;Dj,k (t) 为节点j到节点k的等效距离。
MESV在节点与节点之间的路程、行驶时间和行驶车速的关系为
| TMEi,j,k(t)=Dj,k(t)vMEi(t) | (1) |
| Dj,k(t)=Dj,k[1+1vMEi(t)] | (2) |
| vMEi(t)=vMEi,0(t)e−1.7c | (3) |
式中:viME (t)——第i个MESV的行驶车速;
Dj,k——节点j到节点k的实际距离;
vi,0ME (t)——理想状态下MESV的零流车速;
c——道路拥堵程度。
2 灾前鲁棒优化模型
2.1 目标函数
建立两阶段鲁棒优化模型,确定MESV的配置数量与位置,以最恶劣光伏输出功率场景下的MESV配置成本与负荷削减成本最小为目标函数。第1阶段的决策变量为MESV与节点的连接状态及线路开关状态。第2阶段的决策变量为负荷削减功率、分布式电源输出功率、节点电压、支路功率与电流,光伏输出功率为不确定变量。具体表达式为
| \left\{\begin{array}{l} \min\limits_{\alpha_i^{\mathrm{ME}}, \alpha_{ij}} \max\limits_{P_i^{\mathrm{PV}}} \min\limits_Y\left(\sum\limits_{i \in \mathit{\Omega }_{\mathrm{n}}} C^{\mathrm{ME}} \alpha_i^{\mathrm{ME}}+\omega_i P_i^{\mathrm{LCUT}}\right) \\ Y=\binom{P_i^{\mathrm{LCUT}}, Q_i^{\mathrm{LCUT}}, P_i^{\mathrm{DG}}, Q_i^{\mathrm{DG}}, P_i^{\mathrm{SOP}}, }{P_j^{\mathrm{SOP}}, Q_i^{\mathrm{SOP}}, Q_j^{\mathrm{SOP}}, P_{i j}, Q_{i j}, U_i, I_{i j}} \end{array}\right. | (4) |
式中:αiME——0-1变量,表示MESV与节点i的连接状态,取1时表示有1台MESV与节点i连接,取0时表示没有MESV与节点i连接;
αij——0-1变量,表示支路i - j的连接状态,取1时表示支路i - j连接;取0时表示支路i - j断开;
PiPV——光伏输出功率;
Y——优化变量集合;
Ωn——负荷节点集合;
CME——单位MESV灾前部署成本;
ωi——节点i的单位负荷削减成本;
PiLCUT,QiLCUT——节点i的负荷削减有功功率和无功功率;
PiDG,QiDG——DG输出的有功功率和无功功率;
PiSOP,PjSOP——SOP注入节点i、j的有功功率;
QiSOP,QjSOP——SOP注入节点i、j的无功功率;
Pij,Qij——支路i-j的有功功率和无功功率;
Ui——节点i的电压;
Iij——支路i-j的电流。
由于光伏输出功率具有不确定性,因此采用区间集Us描述预测误差,公式为
| U_{\mathrm{s}}=\left\{(1-\zeta) P_i^{\mathrm{PV}^*} \leqslant P_i^{\mathrm{PV}} \leqslant P_i^{\mathrm{PV}^*}\right\} | (5) |
式中:PiPV*——预测光伏输出功率;
ζ——不确定度。
2.2 约束条件
2.2.1 第1阶段
MESV接入数量约束条件为
| \sum\limits_{i \in \mathit{\Omega }_n} \alpha_i^{\mathrm{ME}}=X_{\max }^{\mathrm{ME}} | (6) |
式中:XmaxME——灾前部署的MESV数量上限。
灾害发生后,可以采用DG单独运行的孤岛方式恢复供电,也可以使用网络重构的方式对线路拓扑进行变化,从而恢复失电负荷。在这个过程中,需要保持配电网拓扑为辐射联通状态。本文采用“单商品流”约束[17]并采用Big-M法对虚拟潮流进行松弛。辐射联通状约束条件为
| \left\{\begin{array}{l} \sum\limits_{i j \in \mathit{\Omega }_{\mathrm{b}}} \alpha_{i j}=N_{\mathrm{b}}-\sum\limits_{i \in \mathit{\Omega }_{\mathrm{n}}} S_i^{\mathrm{VS}} \\ \sum\limits_{j \in \delta(i)} F_{i j}-\sum\limits_{k \in \gamma(i)} F_{k i}=F_i^{\mathrm{VS}}-1 \\ -M_1 S_i^{\mathrm{VS}} \leqslant F_i^{\mathrm{VS}} \leqslant M_1 S_i^{\mathrm{VS}} \\ -M_1 \alpha_{i j} \leqslant F_{i j} \leqslant M_1 \alpha_{i j} \end{array}\right. | (7) |
式中:Ωb——支路集合;
Nb——节点集合;
SiVS——0-1变量,表示虚拟源节点;
δ(i),γ(i)——节点i的子节点集合和父节点集合;
Fij,Fki——支路i - j和支路k - i的虚拟潮流;
FiVS——节点i发出的虚拟有功功率;
M1——无穷大常数。
2.2.2 第2阶段
各节点的MESV与电动汽车输出有功功率不能超过其充放电功率上下限,光伏与柴油发电机的有功功率、无功功率与功率因数也不能超过充放电功率上下限。DG输出功率约束条件为
| P_{i, \min }^{\mathrm{DG}} \leqslant P_i^{\mathrm{DG}} \leqslant P_{i, \max }^{\mathrm{DG}} | (8) |
| Q_{i, \text { min }}^{\mathrm{DG}} \leqslant Q_i^{\mathrm{DG}} \leqslant Q_{i, \text { max }}^{\mathrm{DG}} | (9) |
| P_i^{\mathrm{DG}} \tan \varphi_{\min }<Q_i^{\mathrm{DG}}<P_i^{\mathrm{DG}} \tan \varphi_{\max } | (10) |
式中:Pi, minDG,Pi, maxDG——DG有功功率下限和上限;
PiDG,QiDG——节点i DG的有功功率和无功功率;
Qi, minDG,Qi, maxDG——DG无功功率下限和上限;
φmin,φmax——功率因数角下限和上限。
负荷削减约束条件为
| 0 \leqslant P_i^{\mathrm{LCUT}} \leqslant P_{i, \max }^{\mathrm{L}} | (11) |
| Q_i^{\mathrm{LCUT}}=\frac{Q_{i, \max }^{\mathrm{L}}}{P_{i, \max }^{\mathrm{L}}} P_i^{\mathrm{LCUT}} | (12) |
式中:Pi,maxL,Qi,maxL——负荷有功功率和无功功率上限。
SOP约束条件为
| P_i^{\mathrm{SOP}}+P_j^{\mathrm{SOP}}=0 | (13) |
| \sqrt{\left(P_i^{\mathrm{SOP}}\right)^2+\left(Q_i^{\mathrm{SOP}}\right)^2} \leqslant S_i^{\mathrm{SOP}} | (14) |
| \sqrt{\left(P_j^{\mathrm{SOP}}\right)^2+\left(Q_j^{\mathrm{SOP}}\right)^2} \leqslant S_j^{\mathrm{SOP}} | (15) |
| P_i^{\mathrm{SOP}, \mathrm{L}}=A^{\mathrm{SOP}} \sqrt{\left(P_i^{\mathrm{SOP}}\right)^2+\left(Q_i^{\mathrm{SOP}}\right)^2} | (16) |
| P_j^{\mathrm{SOP}, \mathrm{L}}=A^{\mathrm{SOP}} \sqrt{\left(P_j^{\mathrm{SOP}}\right)^2+\left(Q_j^{\mathrm{SOP}}\right)^2} | (17) |
式中:SiSOP,SjSOP——节点i、j的SOP容量;
PiSOP,L,PjSOP,L——节点i、j的SOP损耗;
ASOP——SOP损耗系数。
对于辐射状配电网,采用DistFlow潮流方程描述。由于网络拓扑结构随线路开关状态发生变化,因此采用Big-M法对电压方程进行松弛。潮流运行约束条件为
| \left\{\begin{array}{l} \sum\limits_{i j \in \mathit{\Omega }_{\mathrm{b}}}\left(P_{i j}-r_{i j} I_{i j}^2\right)+P_i=\sum\limits_{i k \in \mathit{\Omega }_{\mathrm{b}}} P_{i k} \\ \sum\limits_{i j \in \mathit{\Omega }_{\mathrm{b}}}\left(Q_{i j}-x_{i j} I_{i j}^2\right)+Q_i=\sum\limits_{i k \in \mathit{\Omega }_{\mathrm{b}}} Q_{i k} \\ M_1\left(\beta_{i j}-1\right) \leqslant U_i^2-U_j^2+\left(r_{i j}^2+x_{i j}^2\right) I_{i j}^2 \\ -2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right) \leqslant M_1\left(1-\beta_{i j}\right) \\ P_{i j}^2+Q_{i j}^2 \leqslant I_{i j}^2 U_i^2 \\ P_i=P_i^{\mathrm{DG}}-P_i^{\mathrm{PV}}-\lambda_i P_i^{\mathrm{LOAD}}+P_i^{\mathrm{LCUT}} \\ Q_i=Q_i^{\mathrm{DG}}-\lambda_i Q_i^{\mathrm{LOAD}} \\ \left(U^{\mathrm{min}}\right)^2 \leqslant U_i^2 \leqslant\left(U^{\mathrm{max}}\right)^2 \\ I_{i j}^2 \leqslant\left(I^{\mathrm{max}}\right)^2 \end{array}\right. | (18) |
式中:Pik,Qik——支路i-k的有功功率和无功功率;
rij,xij——支路i-j的电阻和电抗;
Pi,Qi——节点i注入的有功功率和无功功率;
βij——0-1变量,表示支路的状态,取1时表示潮流由节点i到节点j,取0时表示潮流由节点j到节点i;
λi——节点i的单位负荷削减成本;
PiLOAD,QiLOAD——节点i处负荷消耗的有功功率和无功功率;
Umax,Umin——系统最大允许电压和最小允许电压;
Imax——系统最大允许支路电流。
利用二阶锥松弛法将原有模型中存在的有关决策变量的二次项与乘积项线性化、凸松弛[18]。首先,对节点电压幅值平方和支路电流幅值平方进行变量替换;然后,对系统潮流约束进行二阶锥松弛;最后,对SOP运行约束式(14)和式(15)进行旋转锥转化,得到公式为
| \left\|\begin{array}{c} 2 P_{i j} \\ 2 Q_{i j} \\ I_{i j}-U_i \end{array}\right\|_2 \leqslant I_{i j}-U_i | (19) |
| \left(P_i^{\mathrm{SOP}}\right)^2+\left(Q_i^{\mathrm{SOP}}\right)^2 \leqslant 2 \frac{S_i^{\mathrm{SOP}}}{\sqrt{2}} \frac{S_i^{\mathrm{SOP}}}{\sqrt{2}} | (20) |
| \left(P_j^{\mathrm{SOP}}\right)^2+\left(Q_j^{\mathrm{SOP}}\right)^2 \leqslant 2 \frac{S_j^{\mathrm{SOP}}}{\sqrt{2}} \frac{S_j^{\mathrm{SOP}}}{\sqrt{2}} | (21) |
3 灾后故障恢复模型
3.1 目标函数
极端灾害发生造成大量负荷失电,因此该阶段以故障时段内负荷削减有功功率最小为目标函数,其公式为
| \min \sum\limits_{t \in \mathit{\Omega }_{\mathrm{T}}} \sum\limits_{i \in \mathit{\Omega }_n} \lambda_i P_{i, t}^{\mathrm{LCUT}} | (22) |
式中:ΩT——故障时段集合;
Pi,tLCUT——t时段节点i的负荷削减有功功率。
该阶段的决策变量为故障时段内SOP发出的有功功率和无功功率、MESV与节点的连接状态、负荷削减有功功率和无功功率、DG发出的有功功率和无功功率、MESV容量、充电桩上的电动汽车容量,以及MESV发出的有功功率和无功功率。
3.2 约束条件
除式(1)至式(3)外,MESV约束还包括时空协同调度约束、连接节点约束、充放电约束和荷电状态约束。MESV约束条件为
| \sum\limits_{i \in \mathit{\Omega }_{\mathrm{ME}}} \alpha_{i, j, t_0}^{\mathrm{ME}}=\alpha_j^{\mathrm{ME}} | (23) |
| \alpha_{i, j, t}^{\mathrm{ME}}+\alpha_{i, k, t+\Delta t}^{\mathrm{ME}} \leqslant 1, \quad \forall \Delta t <T_{i, j, k}^{\mathrm{ME}}(t)+T_0^{\mathrm{ME}} | (24) |
| \sum\limits_{j \in \mathit{\Omega }_n} \alpha_{i, j, t_0}^{\mathrm{ME}} \leqslant 1 | (25) |
| n_{i, t}^{+}+n_{i, t}^{-} \leqslant \sum\limits_{j \in \mathit{\Omega }_n} \alpha_{i, j, t}^{\mathrm{ME}} \alpha_{i, j, t+1}^{\mathrm{ME}} | (26) |
| 0 \leqslant P_{i, t}^{\mathrm{MEch}} \leqslant n_{i, t}^{+} P_{i, \max }^{\mathrm{MEch}} | (27) |
| 0 \leqslant P_{i, t}^{\mathrm{MEdch}} \leqslant n_{i, t}^{-} P_{i, \max }^{\mathrm{MEdch}} | (28) |
| 0 \leqslant Q_{i, t}^{\mathrm{MEch}} \leqslant n_{i, t}^{+} Q_{i, \max }^{\mathrm{MEch}} | (29) |
| 0 \leqslant Q_{i, t}^{\mathrm{MEdch}} \leqslant n_{i, t}^{-} Q_{i, \max }^{\mathrm{MEdch}} | (30) |
| E_{i, t+\Delta t}^{\mathrm{ME}}=E_{i, t}^{\mathrm{ME}}+P_{i, t}^{\mathrm{MEch}} \eta_i^{+} \Delta t-\frac{P_{i, t}^{\mathrm{MEdch}}}{\eta_i^{-}} \Delta t | (31) |
| E_{i, \min }^{\mathrm{ME}} \leqslant E_{i, t}^{\mathrm{ME}} \leqslant E_{i, \max }^{\mathrm{ME}} | (32) |
式中:ΩME——MESV待接入集合;
t0——故障开始时刻;
αi,j,tME——t时段第i个MESV与节点j的连接状态;
k——节点;
Ti,j,kME (t)——第i个MESV从节点j到节点k所需的通行时间;
T0ME——MESV配置时间;
ni,t+,ni,t-——0-1变量,表示充放电;
Pi,tMEch,Pi,tMEdch——t时段MESV的充电有功功率和放电有功功率;
Qi,tMEch,Qi,tMEdch——t时段MESV的充电无功功率和放电无功功率;
Pi,maxMEch,Pi,maxMEdch——MESV充电和放电有功功率上限;
Qi,maxMEch,Qi,maxMEdch——MESV充电和放电无功功率上限;
ηi+,ηi-——MESV充电效率和放电效率;
Ei,tME——t时段MESV容量;
Ei,minME,Ei,maxME——MESV容量下限和上限。
对于式(26)中的非线性项,将其线性化为
| \left\{\begin{array}{l} \alpha_{i, j, t}^{\mathrm{M}} \leqslant \alpha_{i, j, t}^{\mathrm{ME}} \\ \alpha_{i, j, t}^{\mathrm{M}} \leqslant \alpha_{i, j, t+1}^{\mathrm{ME}} \\ \alpha_{i, j, t}^{\mathrm{M}} \geqslant \alpha_{i, j, t}^{\mathrm{ME}}+\alpha_{i, j, t+1}^{\mathrm{ME}}-1 \\ \sum\limits_{j \in \mathit{\Omega }_{\mathrm{n}}} \alpha_{i, j, t}^{\mathrm{M}} \geqslant n_{i, t}^{+}+n_{i, t}^{-} \end{array}\right. | (33) |
式中:αi,j,tM——0-1变量,表示t时段至t + 1时段内第i个MESV与节点j的连接状态。
灾后电动汽车可以向负荷供电,充放电过程需要满足的约束条件为
| \left\{\begin{array}{l} 0 \leqslant P_{i, t}^{\mathrm{EVch}} \leqslant n_{i, t}^{+} P_{i, \max }^{\mathrm{EVch}} \\ 0 \leqslant P_{i, t}^{\mathrm{EVch}} \leqslant n_{i, t}^{-} P_{i, \max }^{\mathrm{EVdch} } \\ n_{i, t}^{+}+n_{i, t}^{-} \leqslant 1 \\ E_{i, \min }^{\mathrm{EV}} \leqslant E_{i, t}^{\mathrm{EV}} \leqslant E_{i, \max }^{\mathrm{EV}} \\ E_{i, t+\Delta t}^{\mathrm{EV}}=E_{i, t}^{\mathrm{EV}}+P_{i, t}^{\mathrm{EVch}} \eta_i^{\mathrm{EVch}} \Delta t-\frac{P_{i, t}^{\mathrm{EVdch}}}{\eta_i^{\mathrm{EVdch}}} \Delta t \end{array}\right. | (34) |
式中:Pi,tEVch,Pi,tEVdch——t时段电动汽车的充电和放电有功功率;
Pi,maxEVch,Pi,maxEVdch——电动汽车的充电和放电有功功率上限;
Ei,tEV——t时段充电桩上的电动汽车容量;
Ei,minEV,Ei,maxEV——电动汽车的容量下限和上限;
ηiEVch,ηiEVdch——电动汽车充电和放电效率。
灾后恢复阶段,模型仍应满足DG输出功率约束、负荷削减约束、SOP约束和潮流运行约束。
3.3 求解方法
灾前鲁棒优化模型的紧凑形式为
| \left\{\begin{aligned} & \min\limits_X \max\limits_{u \in U_{\mathrm{s}}} \min\limits_{Y \in \Omega (X, u)} \boldsymbol{c}_1^{\mathrm{T}} X+\boldsymbol{c}_2^{\mathrm{T}} Y \\ & \text { s.t. } \boldsymbol{A} X \leqslant \boldsymbol{r} \\ & \mathit{\Omega }(X, u)=\{Y \mid \boldsymbol{B} Y \geqslant \boldsymbol{C} X, \boldsymbol{D} Y \geqslant u, \\ &\left.\quad\left\|\boldsymbol{E}_m Y\right\|_2 \leqslant \boldsymbol{f}_m^{\mathrm{T}} Y, m=1, 2, 3, \cdots, n\right\} \end{aligned}\right. | (35) |
式中:X——第1阶段优化变量;
u——第2阶段优化变量;
Us——不确定变量u的区间集;
c1T,c2T,A,B,C,D,Em——系数矩阵;
r,fm——系数向量;
Ω (X,u)——变量Y的可行域。
灾前鲁棒优化问题可分为主问题与子问题。其中:主问题是单层优化问题,属于混合整数二阶锥模型,使用商业求解器gurobi进行求解;子问题是最小化-最优化的双层优化问题,使用yamlip工具箱中的kkt函数转换为单层优化问题后,使用行列生成算法进行求解[19]。灾后恢复模型同样属于混合整数二阶锥模型,使用商业求解器gurobi进行求解。
4 算例分析
4.1 参数设置
为验证所提模型及方法的可行性,在改进IEEE 33节点配电网上进行算例分析[20]。算例电压12.66 kV,额定功率100 MW,有功负荷总量为3 715 kW,无功负荷总量为2 300 kVA。
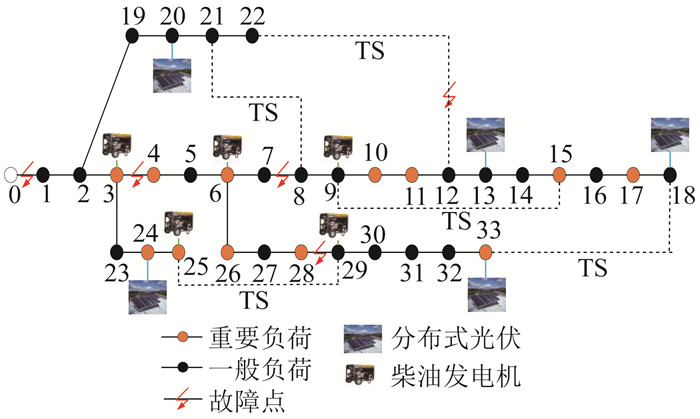
配电网中柴油发电机接入在节点3、9、29、6、25,分布式光伏接入在节点13、18、20、24、33。电动汽车充电桩共3处,分别接入在节点5、15、19。重要负荷为节点3、4、6、10、11、15、17、24、25、26、28、33,节点电压标幺值的允许波动区间为[0.9,1.1]。故障侧电压标幺值最低限值取1.0。配电网拓扑结构如图 5所示。其中,TS为联络开关。
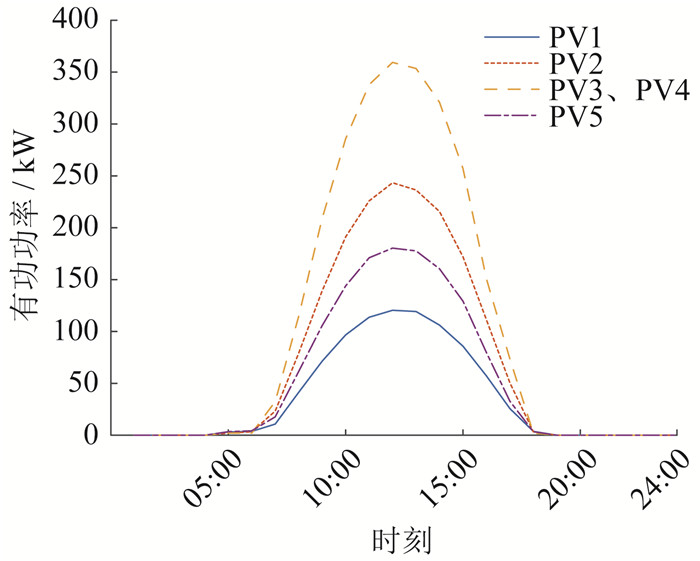
交通网拓扑与配电网相同,相邻电气节点之间的道路距离为2 km,灾害发生时间为08:00,导致配电网与上级电网、支路3-4、7-8、28-29、12-22断开,恢复时长10 h,SOP接入容量为1 MVA,损耗系数为0.02。假设此时MESV与充电桩内的电动汽车均处于满电状态,光伏不确定度ζ为0.35。光伏输出功率预测如图 6所示。
4.2 结果分析
4.2.1 灾前部署分析
灾前部署的MESV数量为2,设置4个方案进行对比。方案1,确定性优化,不考虑MESV部署。方案2,两阶段鲁棒优化,不考虑MESV部署。方案3,确定性优化,考虑MESV部署。方案4,两阶段鲁棒优化,考虑MESV部署。4种方案的部署节点与经济性对比如表 2所示。
表 2
4种方案的部署节点与经济性对比
| 方案 | MESV部署节点 | 成本/元 |
| 1 | 1、1 | 13 389.61 |
| 2 | 22、27 | 10 392.00 |
| 3 | 1、1 | 13 809.56 |
| 4 | 4、25 | 10 809.43 |
由表 2可知,进行MESV灾前部署的成本比不部署的更低,这是因为虽然方案1和方案3省去了MESV部署成本,但需要承担更多的负荷削减成本。此外,由于两阶段鲁棒优化考虑了最恶劣光伏输出功率下的情景,所以制定的方案更保守,成本也略高。
4.2.2 灾后恢复分析
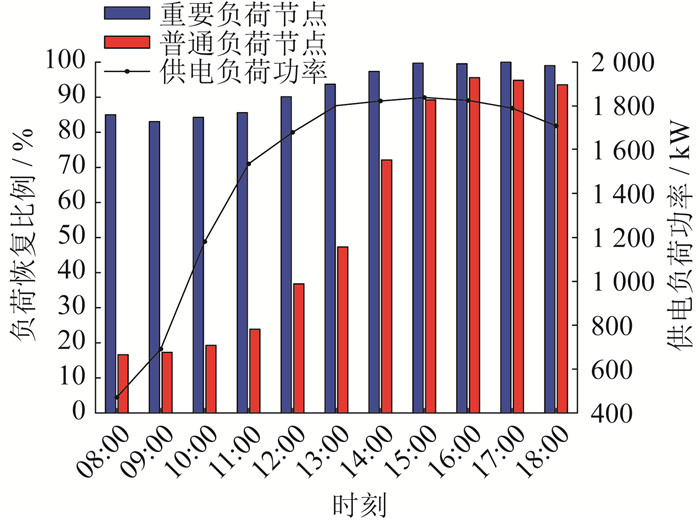
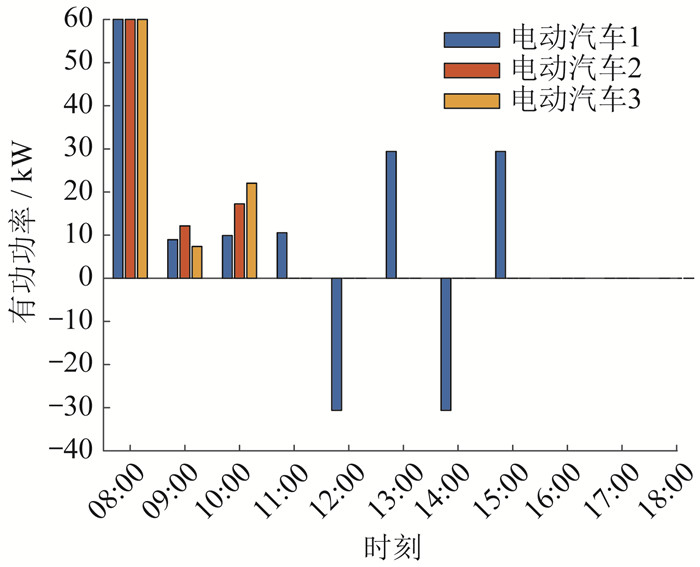
极端灾害发生后,进行多源协同的配电网故障恢复。恢复过程中,若失电区域内有其他电源,SOP的控制模式为PQ控制;若失电区域内没有其他电源,SOP的控制模式为Uf控制。灾后MESV优化调度结果如表 3所示,负荷功率与恢复情况如图 7所示,电动汽车充电和放电功率如图 8所示。
表 3
灾后MESV优化调度结果
| 时刻 | MESV 1部署节点 | MESV 2部署节点 | MESV 1功率/kW | MESV 2功率/kW |
| 08:00 | 25 | 4 | 200 | 170 |
| 09:00 | 25 | 4 | 133 | 57 |
| 10:00 | 25 | 4 | 0 | 60 |
| 11:00 | 17 | 4 | 115 | 61 |
| 12:00 | 17 | 4 | 52 | 0 |
| 13:00 | 17 | 5 | 0 | 71 |
| 14:00 | 7 | 5 | 200 | 0 |
| 15:00 | 7 | 11 | 0 | 70 |
| 16:00 | 6 | 11 | 93 | 100 |
| 17:00 | 6 | 11 | 74 | 0 |
| 18:00 | 6 | 28 | 0 | 82 |
从表 3、图 7和图 8可以看出,2台MESV按照灾前部署接入节点4、节点25,这是由于这些节点均为重要负荷节点。在故障发生时,配电网形成由上级电网、节点4、节点25构成的3个孤岛,此时2台MESV优先恢复节点4、节点25的负荷,恢复完成后,前往下一处节点进行恢复。在灾后恢复过程中,重要负荷恢复比例高于80%。08:00至11:00,由于光照强度的提高,光伏有功功率输出提升,电动汽车处于满电状态,开始向失电负荷放电,MESV开始恢复重要负荷节点4、节点25,供电负荷功率逐步提升,负荷恢复比例快速提升。11:00至13:00,由于光照强度最高,光伏输出功率达到峰值,MESV 1前往重要负荷节点17进行恢复,MESV 2完成节点4的恢复工作后前往节点5。这一阶段尽管电动汽车由放电逐渐转向充电,但整体供电负荷功率仍大幅上升。13:00至16:00,MESV 1先后前往节点7与重要负荷节点6进行恢复,MESV 2完成节点5的恢复工作后前往重要负荷节点11。这一阶段由于光照强度下降,光伏输出功率降低,所以供电负荷功率上升速度变缓。16:00至18:00,MESV1继续恢复重要负荷节点6,MESV2完成节点11的恢复工作后前往重要负荷节点28进行恢复。这一阶段,重要负荷节点恢复已经完成,普通负荷恢复比例较高,但是由于光伏输出功率逐步减少至零以及电动汽车不再放电带来的有功功率下降,所以整体供电负荷功率略有下降。
4.2.3 SOP接入分析
为了验证SOP接入容量对故障恢复过程的影响,分别设置4种方案进行对比。方案1不接入SOP;方案2接入SOP,容量为0.5 MVA;方案3接入SOP,容量为1 MVA;方案4接入SOP,容量为2 MVA。SOP控制模式切换规则为:当SOP两端分别为失电侧和带电侧时,带电侧VSC采用UdcQ控制,失电侧采用Uf控制;当SOP的两端均为带电侧时,则采用UdcQ-PQ控制。18:00时4种方案成本及负荷恢复比例,如表 4所示。
表 4
18:00时4种方案成本及负荷恢复比例
| 方案 | 成本/元 | 负荷恢复比例/% |
| 1 | 34 451 | 98.35 |
| 2 | 32 778 | 99.75 |
| 3 | 30 285 | 100.00 |
| 4 | 31 282 | 99.41 |
由表 4可以看出,接入SOP的方案成本更低,重要负荷恢复比例更高,并且随着SOP接入容量的提升,负荷削减成本逐渐下降。这是由于SOP可以为故障侧提供电压支撑,从而加快负荷恢复进度,且SOP可以为DG提供功率支撑,进一步减少负荷削减成本。当SOP容量增加到2 MVA时,成本不再继续下降,重要负荷恢复比例也有所回落。这是由于随着负荷恢复比例的提高,SOP损耗也在增加,所以导致节点电压下降,制约了故障恢复进程。
5 结论
本文提出含SOP与MESV的两阶段配电网韧性提升策略,建立了灾前鲁棒优化与灾后故障恢复模型,通过算例分析得到如下结论。
(1)由于SOP简单、易控、安全,所以其接入配电网可以为DG与负荷提供功率支撑和电压支撑,加快了故障恢复进度,降低了故障恢复成本。
(2)对MESV进行灾前部署,可以使其灾后迅速参与负荷恢复,降低配电网失负荷风险。
(3)多源协同的灾后故障恢复策略,可以合理利用配电网内灵活的分布式资源和MESV优化调度,能提高负荷恢复比例和配电网韧性。
参考文献
-
[1]陈磊, 邓欣怡, 陈红坤, 等. 电力系统韧性评估与提升研究综述[J]. 电力系统保护与控制, 2022, 50(13): 11-22.
-
[2]刘玉玲, 张峰, 张刚, 等. 考虑分布式电源的配电网灾中-灾后两阶段协同韧性恢复决策[J]. 电力系统自动化, 2024, 48(2): 1-17.
-
[3]杨奕, 刘青, 吴毅, 等. 基于改进萤火虫算法的配电网故障恢复策略[J/OL]. 现代电力: 1-9[2024-02-25]. https://link.Cnki.net/doi/10.19725/j.cnki.1007-2322.2022.0226.
-
[4]李豪, 马驰, 孙菊, 等. 基于改进BPSO算法的含微网的配电网故障恢复方法研究[J]. 电测与仪表, 2022, 59(11): 105-110.
-
[5]徐岩, 张荟, 马天祥, 等. 含分布式电源的配电网故障紧急恢复与抢修协调优化策略[J]. 电力系统自动化, 2021, 45(22): 38-46.
-
[6]马天祥, 王春英, 贾静然, 等. 基于二进制粒子群算法的交直流混合配电网故障恢复方法[J]. 电力系统保护与控制, 2019, 47(9): 112-119.
-
[7]娄铖伟, 张筱慧, 丛鹏伟, 等. 含柔性软开关的有源配电网故障恢复策略[J]. 电力系统自动化, 2018, 42(1): 23-31.
-
[8]王颖, 马佳骏, 王小君, 等. 含智能软开关的配电网重要负荷恢复方法[J]. 电力系统自动化, 2021, 45(8): 104-111.
-
[9]赵晶晶, 李梓博, 刘帅, 等. 考虑智能软开关电压支撑的城市配电网弹性提升方法[J]. 电力建设, 2023, 44(7): 77-86.
-
[10]张璐, 黄睿, 王照琪, 等. 考虑恢复力与经济性均衡的配电网移动储能优化配置策略[J]. 电力系统自动化, 2020, 44(21): 23-31.
-
[11]MA J, FENG X, LEI J, et al. Multi-objective configuration method for mobile energy storage aimed at enhancing the resilience of regional power grid[J]. Journal of Physics, 2023(1): 1742-1745.
-
[12]RAJABZADEH M, KALANTAR M. Improving the resilience of distribution network in coming across seismic damage using mobile battery energy storage system[J]. Journal of Energy Storage, 2022, 52: 104891.
-
[13]王月汉, 刘文霞, 姚齐, 等. 面向配电网韧性提升的移动储能预布局与动态调度策略[J]. 电力系统自动化, 2022, 46(15): 37-45.
-
[14]李明昊, 杨祺铭, 李更丰, 等. 台风场景下基于多种分布式资源协同的弹性配电网两阶段供电恢复策略[J]. 高电压技术, 50(1): 1-16.
-
[15]周晓敏, 葛少云, 李腾. 极端天气条件下的配电网韧性分析方法及提升措施研究[J]. 中国电机工程学报, 2018, 38(2): 505-513.
-
[16]罗轩, 黄云辉, 熊斌宇. 基于配电网-路网融合的移动储能车多场景时空协同优化调度策略[J]. 智慧电力, 2023, 51(8): 30-37.
-
[17]LAVORATO M, FRANCO J F, RIDER M J, et al. Imposing radiality constraints in distribution system optimization problems[J]. IEEE Transactions on Power Systems: A Publication of the Power Engineering Society, 2012, 27(1): 172-180.
-
[18]李振坤, 王法顺, 郭维一, 等. 极端天气下智能配电网的弹性评估[J]. 电力系统自动化, 2020, 44(9): 60-68.
-
[19]邵嗣杨, 马翔, 袁伟, 等. 含电动汽车的不确定性微电网鲁棒优化调度方法[J]. 电气工程学报, 2023, 18(2): 201-209.
-
[20]CAO W Y, WU J Z, JENKINS N, et al. Operating principle of soft open points for electrical distribution network operation[J]. Applied Energy, 2016, 164: 245-257.