|
|
|
发布时间: 2024-06-28 |
控制与检测技术 |
|
|
|
收稿日期: 2024-01-11
基金项目: 上海市扬帆计划项目(22YF1414400)
中图法分类号: TM464
文献标识码: A
文章编号: 2096-8299(2024)03-0242-09
|
摘要
提出了一种基于扩张状态观测器的无源滑模控制(ESOPBSMC)方法,用于提升网侧故障等扰动条件下并网模块化多电平换流器(MMC)的控制性能。该方法从能量角度注入无源阻尼和引入滑模以确保系统渐近稳定,并加速系统收敛,然后通过扩张状态观测器(ESO)观测并补偿各扰动项,以增强系统对干扰的主动抑制能力。仿真结果表明,相较于传统PI控制和PBSMC方法,所提方法具有更快的电流跟踪速度、更强的鲁棒性和更好的环流抑制效果。
关键词
模块化多电平换流器; 无源滑模控制; 扩张状态观测器; PI控制
Abstract
The paper proposes a method of extended state observer based passivity-based sliding mode control (ESOPBSMC) to enhance the control performance of grid-connected modular multilevel converters (MMC) under grid-side fault and other disturbance conditions. This approach injects passive damping from an energy perspective and introduces a sliding mode acceleration system to ensure asymptotic stability and expedite system convergence. Subsequently, it employs an extended state observer (ESO) to observe and compensate for disturbances, thereby enhancing the system's active suppression capability against disturbances. Simulation results demonstrate that compared to traditional proportional-integral(PI)control and passivity-based sliding mode control(PBSMC), the proposed method exhibits faster current tracking speed, stronger robustness, and better circulating current suppression effects.
Key words
modular multilevel converter; passive-based sliding mode control; extended state observer; PI control
随着“双碳”战略目标的提出,我国的电力结构开始逐步向绿色、低碳方向发展转变,可再生能源在现代电力行业中获得了显著的关注。分布式能源的并网问题成为合理利用可再生能源的关键。模块化多电平变流器(Multilevel Modular Converter,MMC)因其具有低开关频率、低谐波失真和模块可扩展性等优势而成为分布式可再生能源并网中最具前景的电力转换设备之一[1]。并网MMC作为新能源和主电网之间的转换设备,受到新能源间歇性和网侧故障的双重影响。这就要求换流器的控制方法既要足够灵活以适应新能源变化,又要具备网侧故障时的稳定运行能力。并网MMC自身的分布式电容也导致了环流,会使上、下桥臂电流发生畸变,增加功率损耗,迫使开关器件需要更大的容量和更强的绝缘能力[2]。因此,在对并网MMC输出电流控制的同时,也要注重对环流的抑制。
目前,并网MMC广泛采用级联比例积分(Proportional Integral,PI)控制,虽然该控制方法简单且易于实现,但由于其局部线性化导致稳定域较窄,当系统受到交流电网故障等外部不确定性扰动或并网MMC内部参数摄动时[3-4],传统PI控制往往无法提供满意的控制性能[5],因此很多非线性方法被用于并网MMC。文献[6]中,MMC系统使用反馈线性化控制器,对系统模型进行输入输出反馈线性化,采用比例谐振(Proportional Resonant,PR)和PI控制器简化设计。然而,由于难以准确测量上、下桥臂平均电容电压,因此MMC控制器设计需考虑子模块电容电压波动的影响。文献[7-8]提出了模型预测控制(Model Predictive Control,MPC),但计算量与子模块数量成正比,在需要电压级别较高或电平数较多的应用中,现有的MPC方案并不总是切实可行。滑模控制(Sliding Mode Control,SMC)具有对参数变化不敏感、抵抗外部干扰能力强的优势,尤其适用于变结构系统[9]。并网MMC是典型的变结构非线性系统,SMC的应用能提高并网MMC在复杂工况下的鲁棒性,但需要以控制输入的抖振为代价[10]。
上述控制器主要基于纯数学理论设计,未考虑受控系统的物理特性。无源控制(PassivityBased Control,PBC)将能量归还给控制,通过分析系统内部动态的能量存储函数,保留对系统有利的耗散项,注入阻尼以确保系统在期望平衡点处渐近稳定[11-12]。虽然PBC具有广泛的稳定域和趋向实现最小能量损失的优势[13],但其仍依赖数学模型的准确性[14]。为增强PBC的鲁棒性,一些学者将PBC与SMC相结合设计了无源滑模控制(Passivity-Based Sliding Mode Control,PBSMC)。文献[15]将PBSMC应用于电力电子变压器,并证明了无源能减弱滑模面的抖振。此外,文献[16]将PBSMC应用于统一潮流控制器,实现了对电压和电流的快速补偿。
尽管PBC在一定程度上减弱了SMC所带来的抖振问题,但两者相结合的方式仍被动地以滑模抖振为代价来实现鲁棒性。相比之下,扩张状态观测器(Extended State Observer,ESO)是一种主动观测系统未建模动态和各种扰动的方法。文献[17]将基于ESO的自适应双环控制应用于电压源型整流器,增强了系统的动态响应和抗扰动能力。文献[18]提出了脉宽调制(Pulse Width Modulation,PWM)整流器的分数阶线性自抗扰控制(Fractional-Order Linear Active Disturbance Rejection Control,FOLADRC),并验证了其对于电网频率变化和电感参数摄动两种情况下的鲁棒性。文献[19]将自适应控制应用于LCL并网逆变器,改善了逆变器的并网电流动态响应和抗参数摄动能力。文献[20]通过自适应控制实现了离散模型下并网MMC的环流抑制。
综上分析,为解决并网MMC在功率变化、电压下降时控制效果不佳的问题,本文提出了一种基于ESO的PBSMC(ESOPBSMC)方法。该方法在并网MMC的欧拉-拉格朗日(Euler-Lagrange,EL)模型的基础上,充分分析输出电流和环流能量动态,利用系统自身的耗散项和阻尼注入加速系统收敛,并引入SMC来提升系统鲁棒性,最后利用ESO主动观测各扰动项并进行补偿,以提升系统的抗干扰能力。
1 并网MMC模型
1.1 并网MMC数学模型
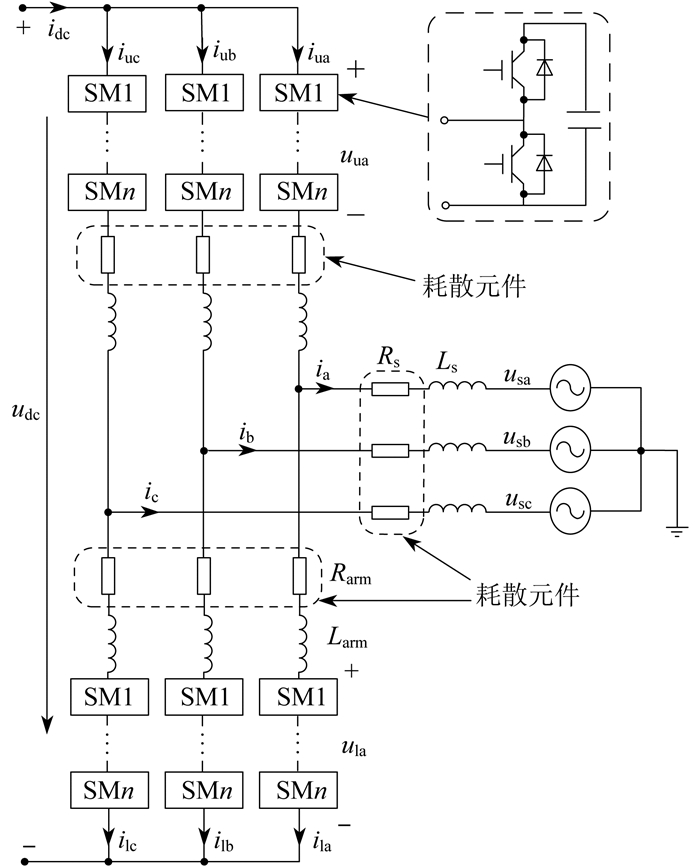
三相并网MMC的基本电路结构如图 1所示。其中,三相交流系统与a、b、c相的中性点相连,每相回路包括上、下两个桥臂,分别连接到直流侧的正极和负极。每个桥臂包括n个子模块SM1~SMn,一个等效桥臂电阻Rarm和一个桥臂电感Larm。等效桥臂阻抗体现了MMC作为无源系统的耗散性,桥臂电感有助于抑制环流交流分量幅值。usk、ik(k=a,b,c)分别为三相交流系统的相电压和相电流;Ls、Rs分别为交流侧的电感和电阻;uua、ula、iua、ila分别为A相上、下桥臂的相电压和相电流;udc、idc分别为直流侧电压、电流。
根据单相上、下基尔霍夫电压定律,可得单相MMC数学表达式如下:
| $ \left\{ \begin{array}{l} u_{\mathrm{s} k}+L_{\mathrm{s}} \frac{\mathrm{d}}{\mathrm{d} t} i_{k}+R_{\mathrm{s}} i_{k}+L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{\mathrm{u} k}+\\ \;\;\;R_{\mathrm{arm}} i_{\mathrm{u} k}-\frac{u_{\mathrm{dc}}}{2}+u_{\mathrm{u} k}=0, k=\mathrm{a}, \mathrm{b}, \mathrm{c} \\ u_{\mathrm{s}k}+L_{\mathrm{s}} \frac{\mathrm{d}}{\mathrm{dt}} i_{k}+R_{\mathrm{s}} i_{k}-L_{\mathrm{arm}} \frac{d}{d t} i_{\mathrm{lk}}- \\ \;\;\;R_{\mathrm{arm}} i_{1 k}+\frac{u_{\mathrm{dc}}}{2}-u_{\mathrm{lk}}=0, \quad k=\mathrm{a}, \mathrm{b}, \mathrm{c} \end{array} \right. $ | (1) |
通过对式(1)的两个公式分别求和、相减,可得并网MMC在abc坐标系下的数学模型如下:
| $ \left\{ \begin{array}{l} L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{\mathrm{cir} k}+R_{\mathrm{arm}} i_{\mathrm{cir} k}-\frac{u_{\mathrm{dc}}}{2}+u_{\mathrm{com} k}=0, k=\mathrm{a}, \mathrm{b}, \mathrm{c}\\ \left(L_{\mathrm{s}}+\frac{L_{\mathrm{arm}}}{2}\right) \frac{\mathrm{d}}{\mathrm{d} t} i_{k}+\left(R_{\mathrm{s}}+\frac{R_{\mathrm{arm}}}{2}\right) i_{k}+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; u_{\mathrm{s} k}-u_{\mathrm{diff}k}=0, \;\;\;\;\;\;\;\; k=\mathrm{a}, \mathrm{b}, \mathrm{c} \end{array} \right. $ | (2) |
式中:icirk——k相环流,icirk =(iuk + ilk)/2;
ucomk——k相共模电压,ucomk =(ulk + uuk)/2;
udiffk——k相差模电压,udiffk =(ulk - uuk)/2。
为简化式(2),令Le = Ls + Larm/2和Re = Rs + Rarm/2分别为等效电感和等效电阻,三相并网MMC在abc坐标系下的数学模型可表示为
| $ \left[\begin{array}{c}L_{\mathrm{e}} \mathrm{d} i_{\mathrm{a}} / \mathrm{dt} \\ L_{\mathrm{e}} \mathrm{d} i_{\mathrm{b}} / \mathrm{dt} \\ L_{\mathrm{e}} \mathrm{d} i_{\mathrm{c}} / \mathrm{dt} \\ L_{\text {arm }} \mathrm{d} i_{\text {cira }} / \mathrm{dt} \\ L_{\text {arm }} \mathrm{d} i_{\text {cirb }} / \mathrm{dt} \\ L_{\text {arm }} \mathrm{d} i_{\text {circ }} / \mathrm{dt}\end{array}\right]=\\ \left[\begin{array}{cccccc}-R_{\mathrm{e}} & 0 & 0 & 0 & 0 & 0 \\ 0 & -R_{\mathrm{e}} & 0 & 0 & 0 & 0 \\ 0 & 0 & -R_{\mathrm{e}} & 0 & 0 & 0 \\ 0 & 0 & 0 & -R_{\text {arm }} & 0 & 0 \\ 0 & 0 & 0 & 0 & -R_{\mathrm{arm}} & 0 \\ 0 & 0 & 0 & 0 & 0 & -R_{\text {arm }}\end{array}\right]\left[\begin{array}{c}i_{\mathrm{a}} \\ i_{\mathrm{b}} \\ i_{\mathrm{c}} \\ i_{\text {cira }} \\ i_{\text {cirb }} \\ i_{\text {circ }}\end{array}\right]+\\ \left[\begin{array}{c}-u_{\mathrm{sa}} \\ -u_{\mathrm{sb}} \\ -u_{\mathrm{sc}} \\ u_{\mathrm{dc}} / 2 \\ u_{\mathrm{dc}} / 2 \\ u_{\mathrm{dc}} / 2\end{array}\right]+\left[\begin{array}{c}u_{\text {diffa }} \\ u_{\text {diffb }} \\ u_{\text {diffc }} \\ -u_{\text {coma }} \\ -u_{\text {comb }} \\ -u_{\text {comc }}\end{array}\right] $ | (3) |
对式(3)中输出电流ik(k=a,b,c)应用传统的dq坐标系Park变换,并对环流icrik(k=a,b,c)应用负序二倍频坐标系Park变换[21]可得
| $ \left\{\begin{array}{l} L_{\mathrm{e}} \frac{\mathrm{d}}{\mathrm{d} t} i_{d}+R_{\mathrm{e}} i_{d}-L_{\mathrm{e}} \omega i_{q}=u_{\mathrm{c} d}-u_{\mathrm{s} d} \\ L_{\mathrm{e}} \frac{\mathrm{d}}{\mathrm{d} t} i_{q}+R_{\mathrm{e}} i_{q}+L_{\mathrm{e}} \omega i_{d}=u_{\mathrm{c} q}-u_{\mathrm{s} q} \\ L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{{\rm{z}} d}+R_{\mathrm{arm}} i_{{\rm{z}} d}-2 \omega L_{\mathrm{arm}} i_{{\rm{z}} q}=u_{\mathrm{z}d} \\ L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{{\rm{z}} q}+R_{\mathrm{arm}} i_{{\rm{z}} q}+2 \omega L_{\mathrm{arm}} i_{{\rm{z}} d}=u_{\mathrm{z}q} \end{array}\right. $ | (4) |
式中:id,iq——MMC三相交流电流的d轴和q轴分量;
ω——电网基波角速度;
ucd,ucq——MMC三相交流电压的d轴和q轴分量;
usd,usq——电网电压的d轴和q轴分量;
izd,izq——环流的d轴和q轴分量;
uzd,uzq——环流压降的d轴和q轴分量。
1.2 并网MMC的EL模型
为了进一步分析并网MMC能量动态,提取能量关系,获得能量存储函数,根据式(4)建立系统的EL模型:
| $ \mathit{\boldsymbol{M}} \dot{\mathit{\boldsymbol{x}}}+\mathit{\boldsymbol{Jx}}+\mathit{\boldsymbol{Rx}}=\mathit{\boldsymbol{U}} $ | (5) |
| $ \boldsymbol{M}=\left[\begin{array}{cccc} L_{\mathrm{e}} & 0 & 0 & 0 \\ 0 & L_{\mathrm{e}} & 0 & 0 \\ 0 & 0 & L_{\mathrm{arm}} & 0 \\ 0 & 0 & 0 & L_{\mathrm{arm}} \end{array}\right] $ | (6) |
| $ \boldsymbol{x}=\left[\begin{array}{llll} i_{d} & i_{q} & i_{{\rm{z}} d} & i_{{\rm{z}} q} \end{array}\right]^{\mathrm{T}} $ | (7) |
| $ \boldsymbol{J}=\left[\begin{array}{cccc} 0 & -\omega L_{\mathrm{e}} & 0 & 0 \\ \omega L_{\mathrm{e}} & 0 & 0 & 0 \\ 0 & 0 & 0 & -2 \omega L_{\mathrm{arm}} \\ 0 & 0 & 2 \omega L_{\mathrm{arm}} & 0 \end{array}\right] $ | (8) |
| $ \boldsymbol{R}=\left[\begin{array}{cccc} R_{\mathrm{e}} & 0 & 0 & 0 \\ 0 & R_{\mathrm{e}} & 0 & 0 \\ 0 & 0 & R_{\mathrm{arm}} & 0 \\ 0 & 0 & 0 & R_{\mathrm{arm}} \end{array}\right] $ | (9) |
| $ \boldsymbol{U}=\left[\begin{array}{llll} u_{\mathrm{c} d}-u_{\mathrm{s} d} & u_{\mathrm{c} q}-u_{\mathrm{s} q} & u_{\mathrm{z}d} & u_{\mathrm{z} q} \end{array}\right]^{\mathrm{T}} $ | (10) |
式中:M,R——并网MMC系统电感和电阻参数矩阵;
x——系统状态变量矩阵;
J——互联矩阵;
U——并网MMC与交流电网之间的能量交换矩阵。
J为反对称矩阵,xTJx =-xTJTx,反映了系统的“无功力”,揭示了系统内部的互联特性。R反映了系统的耗散特性。
2 PBSMC的控制律设计
2.1 控制律推导
通过式(5)的EL模型推导,提取出可以反映能量变化的M矩阵,构建能量存储函数为
| $ H(\boldsymbol{x})=\frac{1}{2} \boldsymbol{x}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{x} $ | (11) |
令状态变量误差矩阵
| $ \tilde{\boldsymbol{x}}=\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}=\left[\begin{array}{c} i_{d}-i_{d\text {ref }} \\ i_{q}-i_{q\text {ref }} \\ i_{\text {z}d}-i_{\text{z}d{\rm{ref}}} \\ i_{{\rm{z}} q}-i_{\text {z}q{\rm{ref}}} \end{array}\right] $ | (12) |
| $ \boldsymbol{x}_{\text {ref }}^{\mathrm{T}}=\left[\begin{array}{llll} i_{d\text{ref }} & i_{q\text {ref }} & i_{\text {z}d{\rm{ref}}} & i_{\text {z}q{\rm{ref}}} \end{array}\right] $ | (13) |
式中:idref,iqref——输出电流id和iq参考值;
izdref,izqref——环流izd和izq参考值。
将状态变量误差矩阵代入能量存储函数,得到误差能量存储函数为
| $ H(\tilde{\boldsymbol{x}})=\frac{1}{2} \tilde{\boldsymbol{x}}^{\mathrm{T}} \boldsymbol{M} \tilde{\boldsymbol{x}} $ | (14) |
对式(14)求导,可得到系统能量变化的趋势,即:
| $ \dot{H}(\tilde{\boldsymbol{x}})=\boldsymbol{M} \tilde{\boldsymbol{x}}^{\mathrm{T}} \dot{\tilde{\boldsymbol{x}}}=\tilde{\boldsymbol{x}}^{\mathrm{T}}\left(\boldsymbol{U}-\boldsymbol{J} \boldsymbol{x}-\boldsymbol{R} \boldsymbol{x}-\boldsymbol{M} \dot{\boldsymbol{x}}_{\mathrm{ref}}\right) $ | (15) |
根据所提供的方程式,通过深入分析并网MMC内部能量动态和充分利用系统固有参数,可实现对不利非线性项的精确补偿。因此,保留并利用反应性能量耗散项,同时对无法利用的其他非线性项进行补偿,从能量耗散的角度得到初步的控制律如下:
| $ \boldsymbol{u}=\boldsymbol{J} \boldsymbol{x}+\boldsymbol{R} \boldsymbol{x}_{\mathrm{ref}}+\boldsymbol{M} \dot{\boldsymbol{x}}_{\mathrm{ref}}+\boldsymbol{v} $ | (16) |
式中:v——附加项,将用于后续阻尼注入和引入SMC。
令U = u,将式(16)代入反应能量变化的能量存储函数式(15)中,得到
| $ \begin{align*} \dot{H}(\tilde{\boldsymbol{x}}) & =-\tilde{\boldsymbol{x}}^{\mathrm{T}} \cdot \boldsymbol{R}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}\right)+\tilde{\boldsymbol{x}}^{\mathrm{T}} \boldsymbol{v} \\ & =-\boldsymbol{R}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}\right)^{2}+\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}\right) \boldsymbol{v} \end{align*} $ | (17) |
式(17)反映了控制律的加入对能量存储函数的影响。其第一项可以加速内部输出电流和环流的误差跟踪速率,其物理解释对应于通过并网MMC的桥臂电阻产生的输出电流和环流的累积热量,因此Rxref被视为有益项保留下来。该有益项反映了系统自身的耗散特性,控制器利用这种耗散性可以加快收敛,因此该耗散项可以被视为MMC本身固有的附加阻尼组成部分。与忽略MMC固有阻尼的其他非线性方法相比,该方法可以用更低的控制成本实现更卓越的瞬态响应。
2.2 附加项设计
设定输出
| $ \dot{H}(\tilde{\boldsymbol{x}})+\boldsymbol{R} \boldsymbol{y}^{\mathrm{T}} \boldsymbol{y}=\boldsymbol{v}^{\mathrm{T}} \boldsymbol{y} $ | (18) |
由于存在额外的阻尼项,能量存储小于能量供应,满足无源条件[22]:
| $ \boldsymbol{v}^{\mathrm{T}} \boldsymbol{y} \geqslant \dot{H}(\tilde{\boldsymbol{x}}) f(\boldsymbol{x}, \boldsymbol{v})+\varepsilon \boldsymbol{y}^{\mathrm{T}} \boldsymbol{y}, \quad \forall(\boldsymbol{x}, \boldsymbol{v}) \in \mathbf{R}^{n} \times \mathbf{R}^{m} $ | (19) |
式中:f(·)——局部Lipschitz函数;
ε——大于零的常数。
因此,可以将并网MMC控制系统视为一个以y为输出、v为输入的无源系统。
需要设计v达到无源控制的目标
| $ \boldsymbol{s}=\left[\begin{array}{llll} s_{1} & s_{2} & s_{3} & s_{4}\end{array}\right]^{\mathrm{T}}=\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}} $ | (20) |
其中,滑模趋近律采用指数趋近律,并采用sat(·)代替sgn(·)以减少滑模抖振问题,设计附加项v为
| $ \boldsymbol{v}=-\boldsymbol{R}_{1}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}\right)-\boldsymbol{k} \boldsymbol{s}-\boldsymbol{\lambda} \operatorname{sat}(\boldsymbol{s}) $ | (21) |
| $ \boldsymbol{R}_{1}^{\mathrm{T}}=\left[\begin{array}{llll} R_{d} & R_{q} & R_{{\rm{z}}d} & R_{{\rm{z}}q} \end{array}\right] $ | (22) |
| $ \boldsymbol{k}^{\mathrm{T}}=\left[\begin{array}{llll} k_{{\rm{s}} d} & k_{{\rm{s}}q} & k_{{\rm{zs}}d} & k_{{\rm{zs}}q} \end{array}\right] $ | (23) |
| $ \boldsymbol{\lambda}^{\mathrm{T}}=\left[\begin{array}{llll} \lambda_{d} & \lambda_{q} & \lambda_{{\rm{z}} d} & \lambda_{{\rm{z}} q} \end{array}\right] $ | (24) |
式中:Rd,Rq,Rzd,Rzq——输入电流和环流无源阻尼注入;
ksd,ksq,kzsd,kzsq——输入电流和环流滑模增益;
λd,λq,λzd,λzq——输入电流和环流滑模面增益。
3 ESOPBSMC的控制律设计
在三相并网MMC运行过程中,三相绕组自感和互感会对桥臂电感产生影响,换流器内温度也会对桥臂电阻有一定影响。此外,并网MMC还要面对功率突变、交流电压下降等外部扰动。如果控制器没有足够的能力来抑制这些干扰,必然会降低闭环系统的性能。因此,本文设计ESO将系统各种扰动集中为一个扩张状态变量矩阵进行补偿。考虑电阻变化量△Re、电感变化量△Le,并网MMC的输出电流和环流数学模型如下:
| $ \left\{\begin{array}{l}L_{\mathrm{e}} \frac{\mathrm{d}}{\mathrm{d} t} i_{d}=u_{\mathrm{c}d}-u_{\mathrm{s} d}-\left(R_{\mathrm{e}}+\Delta R_{\mathrm{e}}\right) i_{d}+\left(L_{\mathrm{e}}+\Delta L_{\mathrm{e}}\right) \omega i_{q} \\ L_{\mathrm{e}} \frac{\mathrm{d}}{\mathrm{d} t} i_{q}=u_{\mathrm{c}q}-u_{\mathrm{s}q}-\left(R_{\mathrm{e}}+\Delta R_{\mathrm{e}}\right) i_{q}-\left(L_{\mathrm{e}}+\Delta L_{\mathrm{e}}\right) \omega i_{d} \\ L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{{\rm{z}} d}=u_{\mathrm{z}d}-\left(R_{\mathrm{arm}}+\Delta R_{\mathrm{arm}}\right) i_{\mathrm{z}d}+\left(L_{\mathrm{arm}}+\Delta L_{\mathrm{arm}}\right) 2 \omega i_{{\rm{z}} q} \\ L_{\mathrm{arm}} \frac{\mathrm{d}}{\mathrm{d} t} i_{\mathrm{z}q}=u_{\mathrm{z}q}-\left(R_{\mathrm{arm}}+\Delta R_{\mathrm{arm}}\right) i_{q}-\left(L_{\mathrm{arm}}+\Delta L_{\mathrm{arm}}\right) 2 \omega i_{{\rm{z}} d}\end{array}\right. $ | (25) |
将电阻变化量和电感变化量以及dq轴耦合量看作扰动,系统的集总扰动可表示为
| $ \left\{\begin{array}{l} f_{d}=-\Delta R_{\mathrm{e}} i_{d}+\Delta L_{\mathrm{e}} \omega i_{q}-\omega L_{\mathrm{e}} i_{q} \\ f_{q}=-\Delta R_{\mathrm{e}} i_{q}-\Delta L_{\mathrm{e}} \omega i_{d}+\omega L_{\mathrm{e}} i_{d} \\ f_{{\rm{z}} d}=-\Delta R_{\mathrm{arm}} i_{{\rm{z}} d}+\Delta L_{\mathrm{arm}} 2 \omega i_{{\rm{z}} q}-2 \omega L_{\mathrm{arm}} i_{{\rm{z}} q} \\ f_{{\rm{z}} q}=-\Delta R_{\mathrm{arm}} i_{{\rm{z}} q}-\Delta L_{\mathrm{arm}} 2 \omega i_{{\rm{z}} d}+2 \omega L_{\mathrm{arm}} i_{{\rm{z}} d} \end{array}\right. $ | (26) |
进而可将式(25)展开后改写为
| $ \left\{\begin{array}{l} \frac{\mathrm{d}}{\mathrm{d} t} i_d=\frac{u_{\mathrm{c} d}-u_{\mathrm{s} d}}{L_{\mathrm{e}}}-\frac{R_{\mathrm{e}}}{L_{\mathrm{e}}} i_d+f_d \\ \frac{\mathrm{d}}{\mathrm{d} t} i_q=\frac{u_{\mathrm{c} q}-u_{\mathrm{s} q}}{L_{\mathrm{e}}}-\frac{R_{\mathrm{e}}}{L_{\mathrm{e}}} i_q+f_q \\ \frac{\mathrm{d}}{\mathrm{d} t} i_{{\rm{z}} d}=\frac{u_{{\rm{z}} d}}{L_{\mathrm{arm}}}-\frac{R_{\mathrm{arm}}}{L_{\mathrm{arm}}} i_{{\rm{z}} d}+f_{{\rm{z}} d} \\ \frac{\mathrm{d}}{\mathrm{d} t} i_{{\rm{z}} q}=\frac{u_{{\rm{z}} q}}{L_{\mathrm{arm}}}-\frac{R_{\mathrm{arm}}}{L_{\mathrm{arm}}} i_{{\rm{z}} q}+f_{{\rm{z}} q} \end{array}\right. $ | (27) |
令系统集总扰动矩阵h = [hd hq hzd hzq]T = [fd/Le fq/Le fzd/Larm fzq/Larm]T。构造标准的输出电流和环流的一阶状态空间为
| $ \left\{\begin{array}{l} \dot{\mathit{\boldsymbol{x}}}=-\frac{\mathit{\boldsymbol{R}}}{\mathit{\boldsymbol{M}}} \mathit{\boldsymbol{x}}+\frac{\mathit{\boldsymbol{U}}}{\mathit{\boldsymbol{M}}}+\mathit{\boldsymbol{h}}\\ \mathit{\boldsymbol{y}}_{1}=\mathit{\boldsymbol{x}} \end{array}\right. $ | (28) |
将式(28)中的h扩张成新的状态变量矩阵,令
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}=-\frac{\boldsymbol{R} \boldsymbol{x}}{\boldsymbol{M}}+\frac{\mathit{\boldsymbol{U}}}{\mathit{\boldsymbol{M}}}+\boldsymbol{h}\\ \dot{\boldsymbol{h}}=\mathit{\boldsymbol{\xi}}(t) \\ \boldsymbol{y}_{1}=\boldsymbol{x} \end{array}\right. $ | (29) |
依据ESO的构造方法[23],可得到观测器的表达式为
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{e}}_{{\bf{1}}}=\mathit{\boldsymbol{z}}_{{\bf{1}}}-\mathit{\boldsymbol{y}}_{{\bf{1}}}\\ \dot{\mathit{\boldsymbol{z}}}_{{\bf{1}}}=\mathit{\boldsymbol{z}}_{{\bf{2}}}+\mathit{\boldsymbol{z}} \frac{{\bf{1}}}{\mathit{\boldsymbol{M}}} \mathit{\boldsymbol{U}}-\frac{\mathit{\boldsymbol{R}}}{\mathit{\boldsymbol{M}}} \mathit{\boldsymbol{z}}_{{\bf{1}}}-\mathit{\boldsymbol{\beta}}_{{\bf{1}}} \mathit{\boldsymbol{e}}_{{\bf{1}}} \\ \dot{\mathit{\boldsymbol{z}}}_{{\bf{2}}}=-\mathit{\boldsymbol{\beta}}_{{\bf{2}}} \mathit{\boldsymbol{e}}_{{\bf{1}}} \end{array}\right. $ | (30) |
式中:z1——系统状态变量矩阵的估计值;
z2——系统集总扰动矩阵的估计值;
β1,β2——观测器输出误差校正增益矩阵。
其中:
| $ \mathit{\boldsymbol{\beta}}_{1}=\left[\begin{array}{llll}\beta_{1 d} & \beta_{1 q} & \beta_{1{\rm{z}}d} & \beta_{1{\rm{z}}q}\end{array}\right]^{\mathrm{T}} $ | (31) |
| $ \mathit{\boldsymbol{\beta}}_{2}=\left[\begin{array}{llll} \beta_{2 d} & \beta_{2 q} & \beta_{2 {\rm{z}} d} & \beta_{2 {\rm{z}} q} \end{array}\right]^{\mathrm{T}} $ | (32) |
式中:β1d,β1q,β2d,β2q——输出电流增益;
β1zd,β1zq,β2zd,β2zq——环流增益。
通过式(20)和式(30),可构造出基于ESO补偿集总扰动后的输出电流无源滑模控制律为
| $ \boldsymbol{u}=\boldsymbol{R} \boldsymbol{x}_{\mathrm{ref}}-\boldsymbol{R}_{1}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{ref}}\right)-\boldsymbol{k} \boldsymbol{s}-\boldsymbol{\lambda} \operatorname{sat}(\boldsymbol{s})-\boldsymbol{f} $ | (33) |
| $ \boldsymbol{f}=\left[\begin{array}{llll} f_{d} & f_{q} & f_{\mathrm{z}d} & f_{\mathrm{z}q} \end{array}\right] $ | (34) |
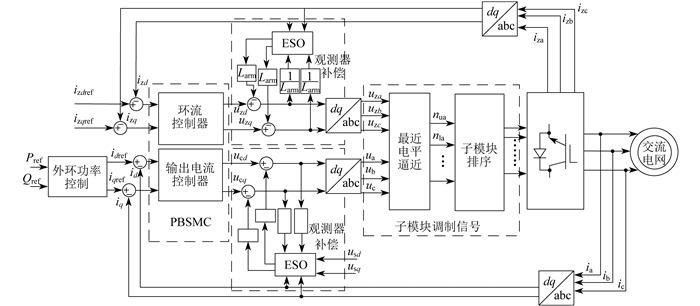
三相并网MMC系统整体的控制框图如图 2所示。其中:Pref、Qref分别为系统有功功率和无功功率的参考值;izk(k=a,b,c)为三相环流;uzk(k=a,b,c)为三相环流压降;uk(k=a,b,c)为换流器输出电压;nua,nla为A相上、下桥臂需要投入的子模块数量。
输出电流和环流经观测器补偿扰动后进行Park逆变换,得到的信号作为最近电平的参考信号,经最近电平调制后得到上、下桥臂的各相电压。最后,经过子模块电压排序决定各子模块的投入或切除。
4 仿真结果与分析
4.1 仿真参数
为评估在各种工作条件下,本文所提ESOPBSMC方法对输出电流和环流的控制性能,在MATLAB/Simulink中搭建了一个21电平的并网MMC模型。在输出电流方面,对比了传统PI、PBSMC、ESOPBSMC 3种方法在有功功率突变、交流电压下降以及参数变化情况下的输出电流控制性能。在环流方面,对比了传统PI和ESOPBSMC方法的环流抑制效果。并网MMC系统参数和控制参数分别如表 1和表 2所示。其中,kp、ki为输出电流的PI控制系数,kzp、kzi为环流的PI控制系数。
表 1
系统参数
| 参数 | 数值 |
| 额定交流频率/Hz | 50 |
| 交流电感/H | 0.013 5 |
| 交流电阻/Ω | 0.35 |
| 直流电压/kV | 5 |
| 单个桥臂子模块数目/个 | 20 |
| 桥臂电感/H | 0.007 5 |
| 桥臂电阻/Ω | 0.2 |
| 子模块电容/μF | 7 000 |
表 2
控制参数
| 控制方法 | 输出电流控制参数 | 环流控制参数 |
| PI | kp = 16,ki = 170 | kzp = 16,kzi = 17 |
| PBSMC | Rd = 80,Rq = 70 | Rzd = Rzq = 10 |
| ksd = 70,ksq = 65 | kzsd = kzsq = 50 | |
| λd = λq = 100 | λzd = λzq = 25 | |
| ESOPBSMC | Rd = 80,Rq = 70 | Rzd = Rzq = 10 |
| ksd = 70,ksq = 65 | kzsd = kzsq = 50 | |
| λd = λq = 100 | λzd = λzq = 25 | |
| β1d = β1q = 100 | β1zd = β1zq = 40 | |
| β2d = β2q = 2 500 | β2zd = β2zq = 400 |
4.2 有功功率突变
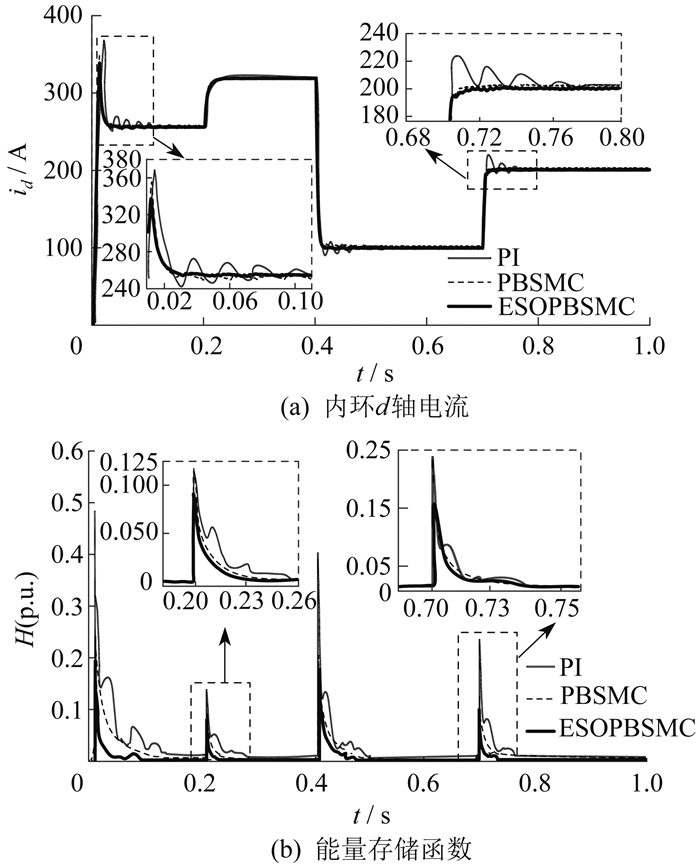
在0~1 s,有功功率经历了4次阶跃变化。在t=0 s时,逆变器启动运行,初始有功功率参考值为1 MW;随后在t=0.2 s时,有功功率参考值增至1.2 MW;在t=0.4 s时,降至0.4 MW;最终在t= 0.7 s时,返回到初始参考值1 MW。有功功率阶跃仿真结果如图 3所示。
图 3展示了有功功率阶跃情况下的内环d轴电流跟踪情况和能量存储函数的变化情况。由图 3(a)可知,传统PI控制方法由于局部线性化,在有功功率阶跃情况下出现了明显的超调和振荡状态,而ESOPBSMC方法相比于PI控制和PBSMC,其超调更小,动态响应速度更快。由图 3(b)可知,ESOPBSMC方法在有功功率阶跃期间具有最小的能量波动。
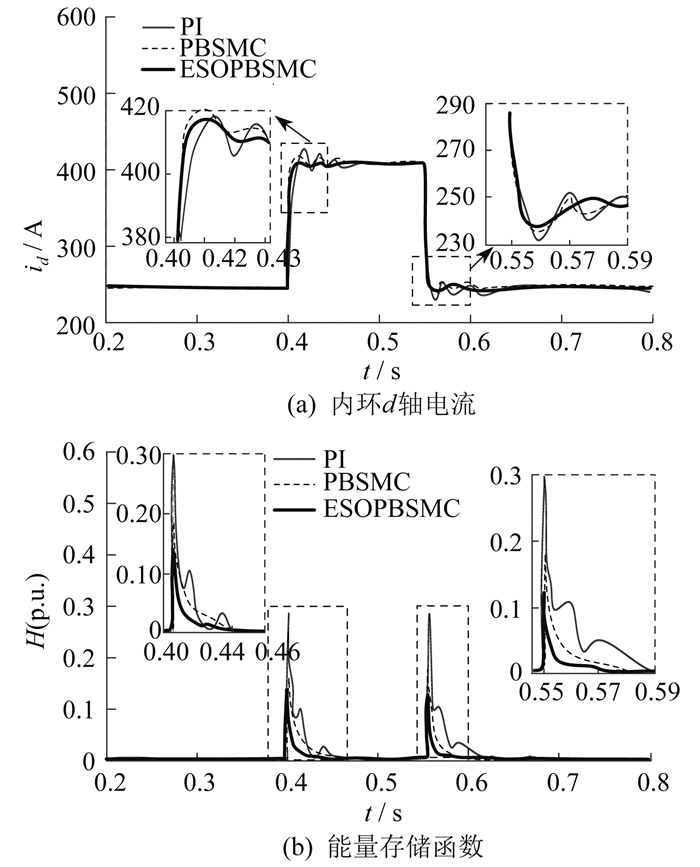
4.3 交流电压下降
4.4 鲁棒性验证
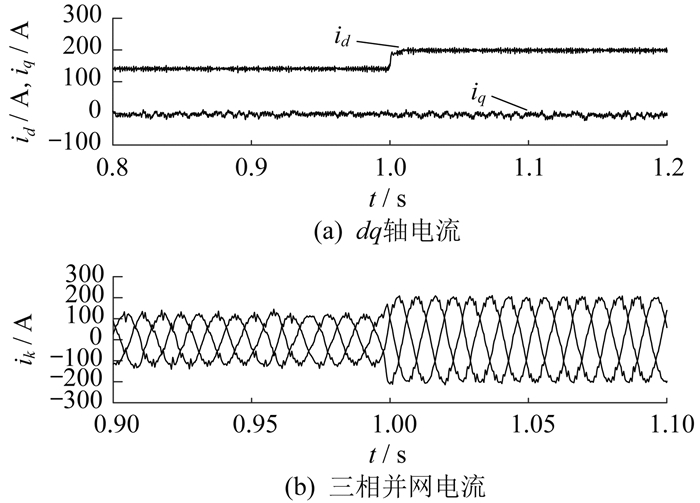
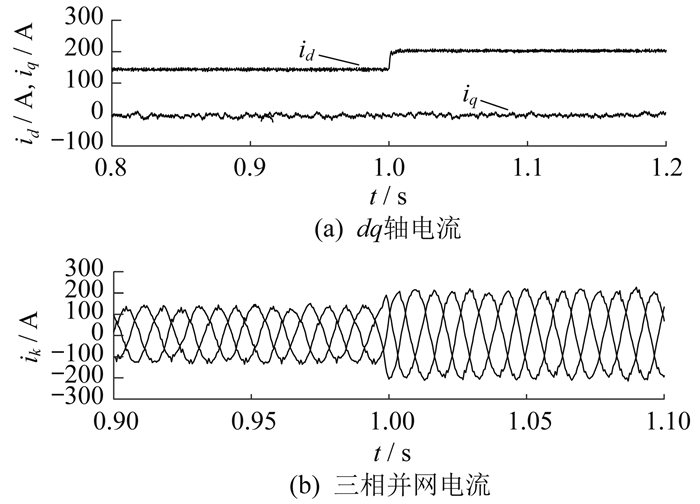
系统运行时参数可能发生较大变化,因此使用电感标称值设计的控制器不能达到准确的控制效果。在t=1 s时,d轴电流参考值由150 A阶跃到200 A。在交流电感Ls和交流电阻Rs均增至额定值的200%的情况下,PBSMC和ESOPBSMC方法内环dq轴电流和三相并网电流分别如图 5、图 6所示。
由图 5和图 6可知:PBSMC和ESOPBSMC方法都能实现对d轴电流的跟踪,各自输出三相并网电流的波形总谐波失真(Total Harmonic Distortion,THD)值分别为6.26% 和2.35%;ESOPBSMC方法的dq轴电流抖振更小且三相并网电流波形畸变更小,这得益于控制器设计时并未采用额定电感,而是采用ESO对扰动的观测值,并进行了补偿。因此,本文所提ESOPBSMC方法对参数摄动具有更好的鲁棒性。
4.5 环流验证
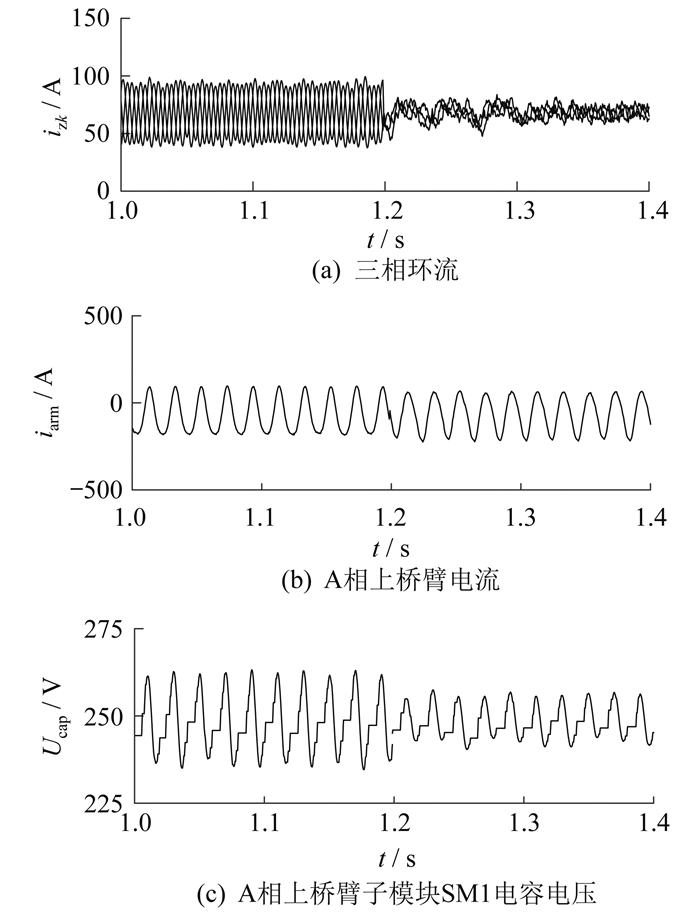
PI控制和ESOPBSMC方法环流抑制仿真结果分别如图 7和图 8所示。
由图 7(a)、图 8(a)可知,在t=1.2 s投入环流抑制器后,两种方法抑制下环流的二倍频分量幅值均减小,但与传统PI控制环流抑制方法相比,本文所提ESOPBSMC方法环流抑制效果更好,这得益于控制器对于MMC自身桥臂电阻的利用以及ESO对各扰动的补偿。由图 7(b)和图 8(b)可以看出,本文所提ESOPBSMC方法抑制下的桥臂电流波形更加对称,显著消除了桥臂电流畸变,波形基本上接近标准的正弦波。由图 7(c)和图 8(c)的A相上桥臂子模块SM1电容电压波形也可以看出,本文所提ESOPBSMC方法环流抑制效果更好,加入PI控制环流控制器后,SM1电容电压波动幅度为235~260 V,而加入ESOPBSMC方法环流抑制器后,SM1电容电压波动范围为240~ 255 V,后者较前者电容电压波动幅度降低了40%。
5 结论
本文针对并网MMC在变工况条件下控制性能效果不佳问题,提出了ESOPBSMC方法。仿真结果表明,在有功功率突变、交流电压下降、参数变化的情况下,本文所提方法具有以下优势。
(1)在输出电流控制方面,相较于传统PI控制、PBSMC方法,ESOPBSMC方法具有更快的跟踪速度、更小的能量变化,且在系统参数变化下依然能实现稳定控制。
(2)在环流方面,相比于传统PI控制,ESOPBSMC方法环流波动更小,减小了环流带来的桥臂电流波形畸变和子模块电压波动。
参考文献
-
[1]陈海燕, 程启明, 韩湘弘, 等. 电网电压不平衡下基于模块化多电平的高压直流输电控制策略[J]. 上海电力大学学报, 2022, 38(2): 128-132.
-
[2]景旭川, 曹以龙, 江友华. PR+虚拟阻抗复合控制的MMC环流抑制策略[J]. 上海电力大学学报, 2021, 37(3): 221-225.
-
[3]LI J K, KONSTANTINOU G, WICKRAMASINGHE H R, et al. Investigation of MMC-HVDC operating region by circulating current control under grid imbalances[J]. Electric Power Systems Research, 2017, 152: 211-222. DOI:10.1016/j.epsr.2017.07.003
-
[4]ABEDINI M, MAHMODI E, MOUSAVI M R, et al. A novel fuzzy PI controller for improving autonomous network by considering uncertainty[J]. Sustainable Energy, Grids and Networks, 2019, 18: 100200. DOI:10.1016/j.segan.2019.100200
-
[5]TU Q, XU Z, XU L. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 2009-2017. DOI:10.1109/TPWRD.2011.2115258
-
[6]YANG S, WANG P, TANG Y. Feedback linearization-based current control strategy for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 161-174. DOI:10.1109/TPEL.2017.2662062
-
[7]MEI H, JIA C, FU J, et al. Low voltage ride through control strategy for MMC photovoltaic system based on model predictive control[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106530.
-
[8]TAVAKOLI S D, FEKRIASL S, PRIETO-ARAUJO E, et al. Optimal H∞ control design for MMC-based HVDC links[J]. IEEE Transactions on Power Delivery, 2021, 37: 786-797.
-
[9]DA SILVA G S, VIEIRA R P, RECH C. Discrete-time sliding-mode observer for capacitor voltage control in modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 876-886. DOI:10.1109/TIE.2017.2721881
-
[10]YANG Q, SAEEDIFARD M, PEREZ M A. Sliding mode control of the modular multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 887897.
-
[11]YANG B, YU T, SHU H, et al. Energy reshaping based passive fractional-order PID control design and implementation of a grid-connected PV inverter for MPPT using grouped grey wolf optimizer[J]. Solar Energy, 2018, 170: 31-46. DOI:10.1016/j.solener.2018.05.034
-
[12]莫栋成, 程启明, 周雅婷. 不平衡电网下MMC-SAPF无源性滑模控制策略研究[J]. 控制工程, 2023, 30(9): 17201729.
-
[13]BERGNA-DIAZ G, ZONETTI D, SANCHEZ S, et al. PI passivity-based control and performance analysis of MMC multiterminal HVDC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(4): 2453-2466. DOI:10.1109/JESTPE.2018.2889152
-
[14]刘道兵, 鲍妙生, 李世春, 等. 不平衡电网下MMC的PCHD模型无源滑模控制策略[J]. 中国电力, 2023, 56(8): 109-116.
-
[15]程启明, 李剑辉, 赖宇生, 等. 非理想条件下基于MMC的电力电子变压器的无源滑模控制策略[J]. 高电压技术, 2023, 49(4): 1556-1566.
-
[16]JIANG C, ZHANG S. Power quality compensation strategy of MMC-UPQC based on passive sliding mode control[J]. IEEE Access, 2023, 11: 3662-3679. DOI:10.1109/ACCESS.2022.3229893
-
[17]HE H, SI T, SUN L, et al. Linear active disturbance rejection control for three-phase voltage-source PWM rectifier[J]. IEEE Access, 2020, 8: 45050-45060. DOI:10.1109/ACCESS.2020.2978579
-
[18]PAN Z, WANG X, ZHENG Z, et al. Fractional-order linear active disturbance rejection control strategy for grid-side current of PWM rectifiers[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 3827-3838. DOI:10.1109/JESTPE.2023.3264481
-
[19]BENRABAH A, XU D G, GAO Z Q. Active disturbance rejection control of LCL-filtered grid-connected inverter using PADé approximation[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6179-6189. DOI:10.1109/TIA.2018.2855128
-
[20]刘炜, 王朝亮, 赵成勇, 等. 基于自抗扰控制原理的MMC-HVDC控制策略[J]. 电力自动化设备, 2015, 35(9): 87-93.
-
[21]杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904.
-
[22]KHALIL H K. Nonlinear systems[M]. 3rd ed. New Jersey, USA: Prentice Hall, 2015: 304.
-
[23]韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 102-159.