|
|
|
发布时间: 2024-06-28 |
控制与检测技术 |
|
|
|
收稿日期: 2024-02-17
基金项目: 国家电网有限公司科技项目(B3094021000B)
中图法分类号: U211
文献标识码: A
文章编号: 2096-8299(2024)03-0251-08
|
摘要
针对轨道交通钢轨扣件绝缘破损导致轨地过渡电阻降低、杂散电流激增进而腐蚀埋地金属结构的问题,提出了钢轨局部绝缘破损时的杂散电流动态分布建模方法。结合轨道交通牵引特性和地电场理论计算轨道交通运行区间内的地电位分布,根据地电位分布及电位梯度评估了钢轨扣件绝缘破损时杂散电流的干扰范围。基于到达时间差(TDOA)定位模型中的Chan算法对地电位时域信号进行两次加权最小二乘法估计,实现了对钢轨绝缘破损点的定位,并分析了算法在不同数量的地电位观测点下的误差和抗噪声能力。仿真验证了破损点定位算法的准确性。
关键词
轨道交通; 杂散电流; 地电位; 钢轨扣件; 绝缘破损; 定位
Abstract
A dynamic distribution modeling method for stray current is proposed to address the problem of insulation damage of rail transit fasteners leading to a decrease in rail to ground transition resistance and a surge in stray current that corrodes buried metal structures. Based on the traction characteristics of the rail transit and the theory of geoelectric field, the dynamic ground potential distribution within the rail transit operating range is calculated. The interference range of stray current during insulation damage of steel rail fasteners is evaluated based on the ground potential distribution and gradient. Based on the Chan algorithm in the TDOA positioning model, a two-step WLS estimation is performed on the time-domain signal of ground potential to locate the point of insulation damage on the steel rail. Finally, the average error and noise resistance of the algorithm under different numbers of ground potential measurement points are analyzed to verify the accuracy of the positioning algorithm.
Key words
rail transit; stray current; ground potential; rail fasteners; insulation damage; positioning
轨道交通直流牵引系统中,常以接触网向列车供电,以行走轨作为回流导体使牵引电流流向变电所负极,形成供电回路。行走轨由钢轨扣件固定在轨枕和道床上,在列车实际运行过程中,行走轨对地产生电位差,使得部分电流沿钢轨扣件流向大地,顺势侵入附近埋地金属,并对其造成电化学腐蚀[1-5]。当钢轨扣件表面积污时,扣件绝缘性能下降,轨地过渡电阻急剧减小,杂散电流泄漏量增大,使附近埋地金属结构被腐蚀的风险显著提升[6]。因此,建立钢轨绝缘破损时杂散电流引起的地电位分布模型,并对绝缘破损点进行定位,在泄漏位置采取相应的防护措施,这对杂散电流的治理具有重要的现实意义。
目前,对杂散电流的分布规律、腐蚀行为、影响因素等方面的研究日趋成熟,针对轨道交通杂散电流分布的仿真模型已经较为完善。在数值模型方面,基于电阻网络模型和CDEGS软件仿真分析,文献[7-9]分别建立了2、3、4层电阻网络模型,通过求解微分方程组得到了杂散电流分布的数学解析式,并讨论了接触网、钢轨、接地网、结构钢筋,以及大地各层电阻、层间过渡电阻等因素对杂散电流分布的影响。文献[10-11]考虑地铁杂散电流与牵引特性之间的动态关系,建立了基于地电位梯度的地铁杂散电流动态干扰模型,通过评估地电位梯度来反映杂散电流的干扰情况,并对土壤电阻率、供电距离、机车取流等影响因素进行了灵敏度分析。文献[12]在电阻网络模型和地电场理论的基础上考虑了地铁牵引特性,建立了杂散电流的地电位动态模型,为杂散电流干扰范围的评估提供了参考。文献[13]将多线路多列车的运行工况等效为多时变电源电阻网络,并基于地电场理论计算得出了地电位的实时分布。文献[14-15]将钢轨扣件等效为绝缘层,讨论了过渡电阻对杂散电流分布的影响。文献[16]对绝缘层局部破损条件下杂散电流及电位梯度的动态分布进行了计算和分析。
杂散电流的总体防护原则是以防为主、以排为辅,当出现不可避免的杂散电流危害时,唯一的解决方法是在危害区域增加防护手段。当钢轨扣件绝缘电阻降低导致杂散电流增大时,对其进行准确定位才可以从源头上解决干扰问题。目前,针对钢轨绝缘破损点定位问题的研究成果相对较少。文献[17]以仿真数据训练神经网络,通过钢轨电流、电位和排流网电位、电流等因变量参数反演得到定位结果。文献[18]利用光纤光栅测量钢轨扣件压降来评估其绝缘性能,通过大范围布置光纤光栅,实现对绝缘破损点的定位。
到达时间差(Time Difference Of Arrival,TDOA)定位原理是通过计算信号到达时间差来确定信号源的位置,以其定位精度高、复杂性低等优点被广泛应用于卫星导航、水下声源定位等领域。在TDOA定位模型的诸多算法中,Chan算法因其具有不需要初值、视距环境下定位精度高、抗高斯噪声能力强等优势,越来越受到重视。文献[19-20]基于Chan算法实现了对海上声源和锅炉四管泄漏点的定位。
本文建立了钢轨扣件绝缘破损时的动态杂散电流分布模型,根据轨道交通牵引特性求解得到运行区间内任意时刻的杂散电流分布,基于地电场理论计算该条件下地电位动态分布,与绝缘无损情况下的地电位进行对比,评估扣件绝缘破损造成的干扰范围。结合TDOA定位模型中的Chan算法,提出了一种针对钢轨扣件绝缘破损的定位方法,并从定位误差、定位标准差以及抗噪声能力等方面对定位性能进行分析。
1 杂散电流引起地电位波动的理论分析
轨道交通运行轨道由钢轨扣件固定在道床上,单个扣件可以等效为大电阻和小电容的并联电路。当列车运行时,行走轨对地产生电压差,部分电流通过电阻回路侵入大地,且侵入电流大小受扣件电阻的影响。虽然轨道交通是直流供电,但牵引电流在运行过程中难免产生波动,尤其是在列车加速、制动过程中,牵引电流的大小会产生明显变化。此时,也会有部分电流通过电容回路泄漏。这部分电流通常极小,不会对列车运行和埋地金属造成影响。因此,轨道交通杂散电流的泄漏量主要取决于牵引电流的大小和钢轨扣件的绝缘性能。
1.1 轨道交通牵引特性
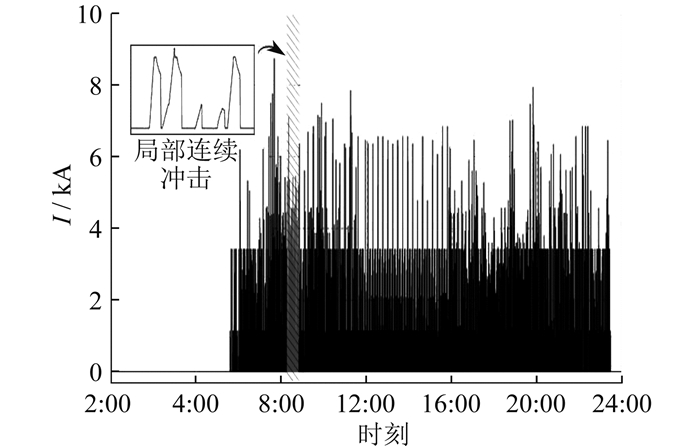
轨道交通在运行过程中启停频繁,供电系统的牵引电流会随着列车的运行状态发生周期性变化,可以分为牵引加速过程、惰行过程和制动减速过程3个阶段。当列车牵引加速时,会在数十秒内产生数兆瓦的正向牵引功率,列车制动时则会产生一个反向的负功率。在轨道交通实际运行过程中,制动产生的负功率通常无法反馈到主变压器。当线路上有多辆列车连续启动时,行走轨上的回流电流就会表现出连续的正极性冲击特性。使用PSCAD软件搭建轨道交通配电线路,结合轨道交通电气设备参数、运行时刻表、线路及主变损耗等数据复现轨道交通供电系统,可以计算出流经行走轨回流电流I的变化特性[21-22]。流经行走轨回流电流的变化特性如图 1所示。
由图 1可以看出,当多列车同时处于牵引加速状态时,牵引电流成倍增加,因此在早晚交通高峰时线路上同时运行的列车较多,主变压器负载较大,流经行走轨回流电流普遍更高。考虑到计算效率,本文选取早高峰时段时长为250 s的局部连续冲击电流作为杂散电流计算的边界条件。
1.2 绝缘破损下的地电位分布模型
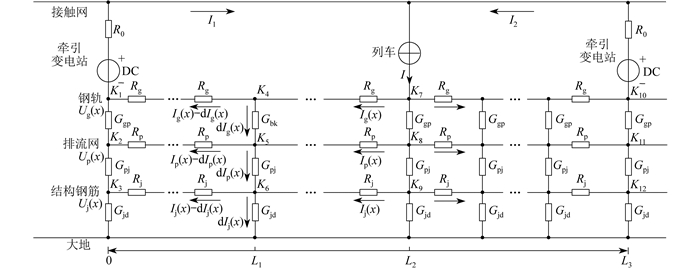
在计算轨道交通杂散电流时,通常需要构建轨道交通系统的电阻网络模型,通过求解微分方程组得到轨道交通全线钢轨电位、泄漏电流等参数随时间的变化情况。本文对轨道交通单个运行区间建立“钢轨—排流网—结构钢筋—大地”4层电阻网络的双边供电模型,轨道交通供电系统的等效回路如图 2所示。其中:R0、Rg、Rp、Rj分别为牵引变电站等效电阻、钢轨单位长度纵向电阻、排流网单位长度纵向电阻、结构钢筋单位长度纵向电阻;I1、I2、I分别为左牵引站输出电流、右牵引站输出电流、列车回流电流;Kq(q=1,2,3,…,12)为计算节点;Ggp、Gpj、Gjd、Gbk分别为钢轨对排流网的单位长度电导、排流网对结构钢筋的单位长度电导、结构钢筋对大地的单位长度电导、绝缘破损处钢轨对排流网的单位长度电导;Ug(x)、Up(x)、Uj(x)分别为x m处钢轨对地、排流网对地、结构钢筋对地的动态电压;Ig(x)、Ip(x)、Ij(x)分别为x m处流经钢轨、排流网、结构钢筋的动态电流;0—L1、L1—L2、L2—L3为划定的计算区间。
基于基尔霍夫电流电压定律,区域L1—L2的单个等效微元电路的微分方程组如下:
| $ \left\{\begin{array}{l} \mathrm{d} U_{\mathrm{g}}(x)=I_{\mathrm{g}}(x) R_{\mathrm{g}} \mathrm{d} x-I_{\mathrm{p}}(x) R_{\mathrm{p}} \mathrm{d} x \\ \mathrm{~d} I_{\mathrm{g}}(x)=U_{\mathrm{g}}(x) G_{\mathrm{bk}} \mathrm{d} x \\ \mathrm{~d} U_{\mathrm{p}}(x)=I_{\mathrm{p}}(x) R_{\mathrm{p}} \mathrm{d} x-I_{\mathrm{j}}(x) R_{\mathrm{j}} \mathrm{d} x \\ \mathrm{~d} I_{\mathrm{p}}(x)=U_{\mathrm{p}}(x) G_{\mathrm{pj}} \mathrm{d} x-U_{\mathrm{g}}(x) G_{\mathrm{bk}} \mathrm{d} x \\ \mathrm{~d} U_{\mathrm{j}}(x)=I_{\mathrm{j}}(x) R_{\mathrm{j}} \mathrm{d} x \\ \mathrm{~d} I_{\mathrm{j}}(x)=U_{\mathrm{j}}(x) G_{\mathrm{jd}} \mathrm{d} x-U_{\mathrm{g}}(x) G_{\mathrm{pj}} \mathrm{d} x \end{array}\right. $ | (1) |
整理后,将微分方程组的求解结果以矩阵形式表示,可得:
| $ \left[\begin{array}{llllll}k_{11} & k_{12} & k_{13} & k_{14} & k_{15} & k_{16} \\ k_{21} & k_{22} & k_{23} & k_{24} & k_{25} & k_{26} \\ k_{31} & k_{32} & k_{33} & k_{34} & k_{35} & k_{36} \\ k_{41} & k_{42} & k_{43} & k_{44} & k_{45} & k_{46} \\ k_{51} & k_{52} & k_{53} & k_{54} & k_{55} & k_{56} \\ k_{61} & k_{62} & k_{63} & k_{64} & k_{65} & k_{66}\end{array}\right]\left[\begin{array}{l}C_{1} \mathrm{e}^{\lambda_{1} x} \\ C_{2} \mathrm{e}^{\lambda_{2} x} \\ C_{3} \mathrm{e}^{\lambda_{3} x} \\ C_{4} \mathrm{e}^{\lambda_{4} x} \\ C_{5} \mathrm{e}^{\lambda_{5} x} \\ C_{6} \mathrm{e}^{\lambda_{6} x}\end{array}\right]=\left[\begin{array}{c}I_{\mathrm{g}}(x) \\ U_{\mathrm{g}}(x) \\ I_{\mathrm{p}}(x) \\ U_{\mathrm{p}}(x) \\ I_{\mathrm{j}}(x) \\ U_{\mathrm{j}}(x)\end{array}\right] $ | (2) |
式中:kij——待定系数,i、j=1,2,3,4,5,6;
λi——系数矩阵的特征值;
Ci——钢轨、排流网和结构钢筋电阻层的电流电位求解系数,可根据电阻网络的边界条件得到。
在理想条件下,L1—L2区域的起始边界条件为
| $ \left\{\begin{array}{l} I_{\mathrm{g}}(0)=I_{1} \\ U_{\mathrm{g}}(0)=U_{\mathrm{N}} \\ I_{\mathrm{p}}(0)=0 \\ U_{\mathrm{p}}(0)=0 \\ I_{\mathrm{j}}(0)=0 \\ U_{\mathrm{j}}(0)=0 \end{array}\right. $ | (3) |
式中:UN——列车所处位置钢轨对地电压。
将式(3)代入式(2),即可得到L1—L2区域钢轨、排流网、结构钢筋的电压和入地电流。以此方法,依次求解各区域微分方程组,可以得到轨道交通全线的钢轨电位和杂散电流分布情况。
将微分区间流入大地的电流等效为离散点电流源。根据点电流源I0(x0,y0,z0)在土壤的电场分布解析式,大地中任意一点P(x,y,z)的电位U(x,y,z)为
| $ U(x, y, z)=\frac{\rho I}{2 {\mathsf{π}} \sqrt{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}+\left(z-z_{0}\right)^{2}}} $ | (4) |
式中:ρ——土壤电阻率;
I——点电流源电流。
由于杂散电流在钢轨上是连续分布的,将杂散电流分布的解析式代入式(4)并沿0—L3区间积分,便可得到轨道交通任意时刻沿线土壤电位分布的情况。
2 仿真与分析
2.1 CDEGS软件仿真
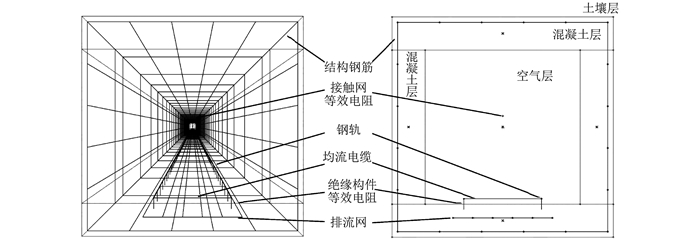
相关研究结果表明,CDEGS软件仿真与电阻网络理论计算结果之间的误差极小,并且CDEGS软件仿真相比理论模型的边界条件更符合实际工程环境。因此,本文选择CDEGS软件中的MALZ模块,对上海某段长2 km的轨道交通线路进行建模分析。仿真模型的结构透视图和截面图如图 3所示。其中,隧道口深10 m,钢轨间隔为1.4 m,混凝土层厚度为0.6 m。
空间结构为“空气—混凝土—土壤”3层传导介质,主要导流金属结构为“接触网—钢轨—排流网—结构钢筋”4层导体结构。接触网、牵引变电所、单根钢轨和列车均等效为单根导体,钢轨间设置均流电缆,每个钢轨扣件均等效为单根导体,扣件的布置间隙为0.5 m。仿真模型的结构参数如表 1所示。
表 1
仿真模型的结构参数
| 钢轨/排流网/结构钢筋 | 钢轨扣件 | 破损扣件 | ||||||
| 纵向电阻/(n/km) 半径/ | m | 数量/个 | 半径/m | 阻值/n | 半径/m | 阻值/Mn | ||
| 0.035/0.660/0.320 | 0.025/0.008/0.012 5 | 6 000 | 0.01 m | 1.587×1010 | 0.01 | 1 | ||
| 接触网 | 土壤层/混凝土层/空气层 | |||||||
| 纵向电阻/n | 半径/m | 涂层类型 | 电阻率/(n*m) | 相对磁导率(p.u.) | 相对介电常数(p.u.) | |||
| 0 | 0.03 | 绝缘 | 100/200/1.0×1018 | 1.0/1.0/1.0 | 15.0/15.0/1.0 | |||
以常见的轨道交通弹条三型扣件为例,全新的钢轨扣件绝缘电阻通常在1.0×108 Ω以上。运行一段时间后,钢轨扣件表面积压的污秽吸收了空气中的水汽,在扣件表面形成了高电导率层,导致绝缘性能大幅下降。当污秽层电导率为0.001 S/m时,绝缘电阻会下降到100 kΩ左右。每1 km钢轨扣件的数量设置为2 000个,此时可以通过修改绝缘扣件阻值实现对任意绝缘破损点的模拟。
2.2 结果分析
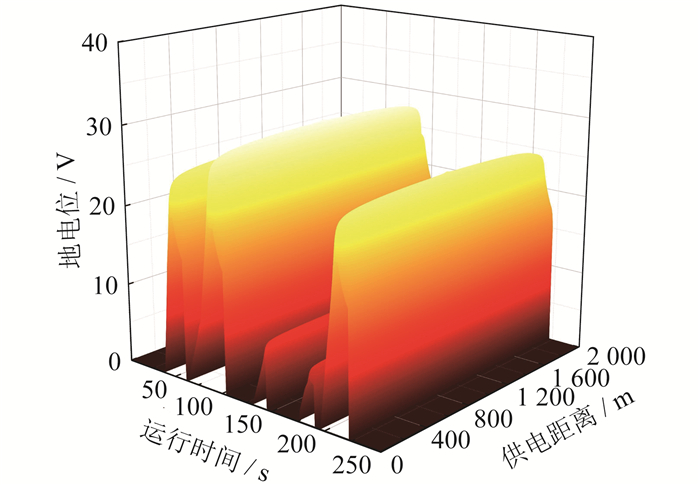
从全天回流电流特性中选取250 s的电流时域数据代入杂散电流分布模型,计算得出轨道交通运行区间的地表电位分布。扣件无绝缘破损时的地电位分布如图 4所示。
由图 4可知,当钢轨扣件无绝缘破损时,轨道交通运行区间内地电位分布均匀,列车所处位置电位绝对值最高。同时,地电位波动特性与牵引电流特性呈正相关,运行89.01 s时地电位达到最大值29.41 V。
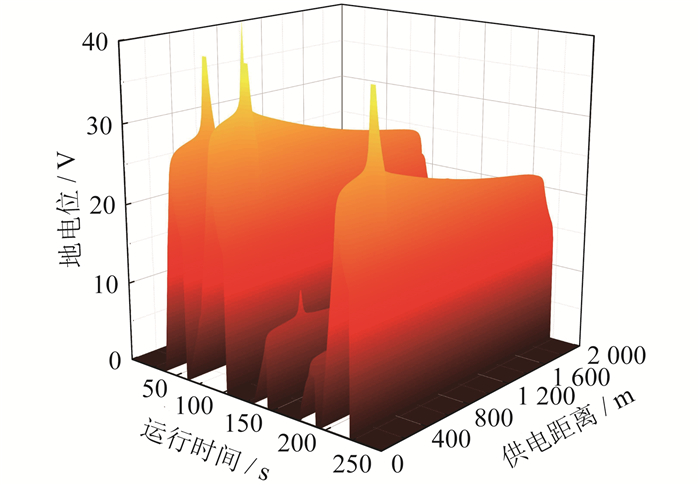
将单根钢轨300 m处扣件的电阻特性设为绝缘破损,重新计算杂散电流分布,得到的单个扣件绝缘破损时轨道交通运行区间地电位分布如图 5所示。
由图 5可知,单个绝缘破损点会对整个运行区间的地电位分布产生影响。绝缘破损扣件所处位置电位绝对值最高,以破损点为中心半径100 m的范围内地电位均有十分明显的提升,运行89.01 s时地电位达到最大值43.23 V,比绝缘无损时增大了46.9%。
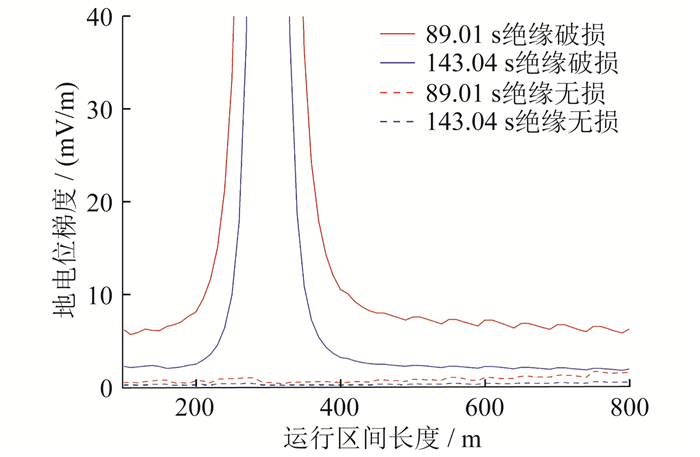
GB/T 50991—2014《埋地钢质管道直流干扰防护技术标准》中指出,当地电位梯度大于或等于2.5 mV/m时,应当对埋地管道设置直流防护措施。根据轨道交通沿线的地电位分布,计算相应的地电位梯度变化,如图 6所示。其中,89.01 s为线路上多机车同时加速、牵引电流达到峰值的时刻,143.04 s为单机车加速牵引电流达到峰值的时刻。这两个时刻的地电位梯度分别反映了多机车和单机车启动工况下杂散电流干扰最严重的情况。
由图 6可知,当钢轨扣件绝缘状态良好时,即使在早高峰多机车同时启动的工况下,轨道交通沿线的地电位梯度也始终处于标准规定的安全阈值以下;当扣件出现绝缘破损时,破损点处地电位梯度将远远高于安全标准。根据计算结果可知,单机车启动工况下,破损点处地电位梯度最高可达140.56 mV/m,并对其周边超过100 m的范围造成影响;多机车启动时,有可能使超过1 000 m的区域受到明显的杂散电流干扰。在确定了绝缘破损造成的杂散电流干扰范围后,可通过TDOA定位原理对其进行定位。因此,若通过地电位信号对绝缘破损点进行定位,应当保持所有地表探测基站距离绝缘破损点投影位置不超过1 000 m。
3 绝缘破损点定位原理
TDOA是通过计算信号到达时间差来确定信号源的位置,在水下声源定位、卫星定位、通信等领域有着广泛的应用。设绝缘破损扣件三维坐标为(xu,yu,zu),地电位探测点n的坐标为(xn,yn,0)(n=1,2,3,…,N),N为探测点数量。探测点与绝缘破损点间的距离Dn满足
| $ D_{n}^{2}=v^{2} t_{n}^{2}=\left(x_{n}-x_{\mathrm{u}}\right)^{2}+\left(y_{n}-y_{\mathrm{u}}\right)^{2}+{z_{\mathrm{u}}}^{2} $ | (5) |
| $ v=\frac{C}{\sqrt{\mu_{\mathrm{r}} \varepsilon_{\mathrm{r}}}} $ | (6) |
式中:v——土壤中电磁波传播速度;
tn——信号到达探测点n的时间;
μr——土壤相对磁导率;
εr——土壤相对介电常数。
令xn,1=xn-x1,yn,1=yn-y1,Rn=xn2+yn2,可得:
| $ D_{n, 1}=D_{n}-D_{1}=\sqrt{\left(x_{n}-x_{\mathrm{u}}\right)^{2}+\left(y_{n}-y_{\mathrm{u}}\right)^{2}+{z_{\mathrm{u}}}^{2}}-\\ \;\;\;\;\;\;\;\; \sqrt{\left(x_{1}-x_{\mathrm{u}}\right)^{2}+\left(y_{1}-y_{\mathrm{u}}\right)^{2}+{z_{\mathrm{u}}}^{2}} $ | (7) |
当N=4时,联立3个TDOA方程即可实现对定位目标的三维坐标求解。当N>4时,非线性方程组会出现测量冗余量,导致方程组无解。此时引入Chan算法可以充分利用冗余数据,提高定位的准确性。
将TDOA方程组进行线性化处理后计算初步定位结果,令
| $ \begin{align*} & \boldsymbol{G}_{\mathrm{a}}=-\left[\begin{array}{cccc} x_{2, 1} & y_{2, 1} & 0 & D_{2, 1} \\ x_{3, 1} & y_{3, 1} & 0 & D_{3, 1} \\ \vdots & \vdots & \vdots & \vdots \\ x_{N, 1} & y_{N, 1} & 0 & D_{N, 1} \end{array}\right] \end{align*} $ | (8) |
| $ \begin{align*} \boldsymbol{H}_{\mathrm{a}}=\frac{1}{2}\left[\begin{array}{c} D_{2, 1}^{2}+R_{1}-R_{2} \\ D_{3, 1}^{2}+R_{1}-R_{3} \\ \vdots \\ D_{N, 1}^{2}+R_{1}-R_{N} \end{array}\right] \end{align*} $ | (9) |
测量过程中存在噪声和误差,令误差向量ψ为
| $ \boldsymbol{\psi}=\boldsymbol{H}_{\mathrm{a}}-\boldsymbol{G}_{\mathrm{a}} \boldsymbol{Z}_{\mathrm{a}} $ | (10) |
| $ \boldsymbol{\gamma}=\boldsymbol{E}\left(\boldsymbol{\psi} \boldsymbol{\psi}^{\mathrm{T}}\right)=v^{2} \boldsymbol{B} \boldsymbol{Q} \boldsymbol{B} $ | (11) |
式中:Za——未知矢量,通过第一次加权最小二乘法估计得到;
γ——误差向量的协方差矩阵;
E——矩阵期望;
Q——TDOA测量值的协方差矩阵;
B=diag(D2,D3,D4,…,DN)。
假设Za各元素独立,通过加权最小二乘法计算得到的第一次估计值为
| $ \boldsymbol{Z}_{\mathrm{a}}=\left(\boldsymbol{G}_{\mathrm{a}}{ }^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{G}_{\mathrm{a}}\right)^{-1} \boldsymbol{G}_{\mathrm{a}}{ }^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{H}_{\mathrm{a}} $ | (12) |
实际上Za各元素相关,因此第一次估计结果存在误差。将第一次估计得到的初值 Za代入式(10)得到ψ的近似值,接着进行第二次估计,令
| $ \boldsymbol{Z}_{\mathrm{b}}=\left(\boldsymbol{G}_{\mathrm{b}}^{\mathrm{T}} \boldsymbol{\gamma}_{\mathrm{b}}^{-1} \boldsymbol{G}_{\mathrm{b}}\right)^{-1} \boldsymbol{G}_{\mathrm{b}}^{\mathrm{T}} \boldsymbol{\gamma}_{\mathrm{b}}^{-1} \boldsymbol{H}_{\mathrm{b}} $ | (13) |
其中,
| $ \boldsymbol{G}_{\mathrm{b}}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \end{array}\right] $ | (14) |
| $ \boldsymbol{H}_{\mathrm{b}}=\left[\begin{array}{c} \left(\boldsymbol{Z}_{\mathrm{a}}(1)-x_{1}\right)^{2} \\ \left(\boldsymbol{Z}_{\mathrm{a}}(2)-y_{1}\right)^{2} \\ \left(\boldsymbol{Z}_{\mathrm{a}}(3)\right)^{2} \\ {D_{1}}^{2} \end{array}\right] $ | (15) |
| $ \boldsymbol{\gamma}_{\mathrm{b}}=4 \boldsymbol{B}_{\mathrm{b}} \operatorname{cov}\left(\boldsymbol{Z}_{\mathrm{a}}\right) \boldsymbol{B}_{\mathrm{b}} $ | (16) |
| $ \boldsymbol{B}_{\mathrm{b}}=\operatorname{diag}\left[\boldsymbol{Z}_{\mathrm{a}}(1)-x_{1}, \boldsymbol{Z}_{\mathrm{a}}(2)-y_{1}, \boldsymbol{Z}_{\mathrm{a}}(3), D_{1}\right. $ | (17) |
式中:Za(m)——Za的第m行元素,m=1,2,3。
目标的最终定位估计值Z为
| $ \boldsymbol{Z}= \pm \sqrt{\boldsymbol{Z}_{\mathrm{b}}}+\left[\begin{array}{c} x_{1} \\ y_{1} \\ 0 \end{array}\right] $ | (18) |
4 定位结果分析
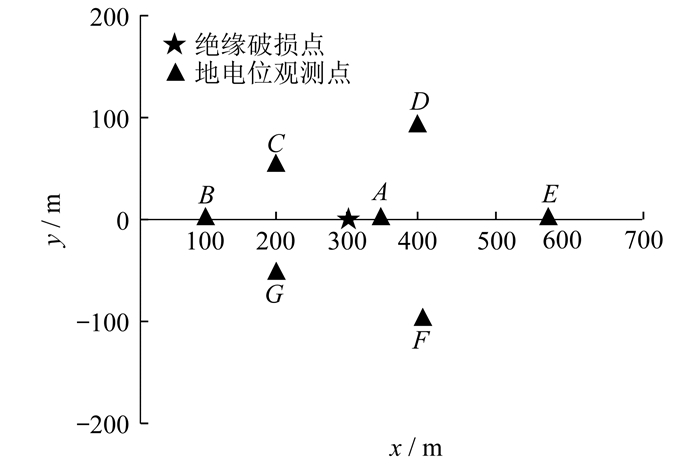
在仿真中增设7个地表观测点,记录地表电位的时域波形,并分别计算4~7个探测点时算法的定位误差。地电位观测点位置如图 7所示。
为提高定位精度,在杂散电流的影响区间内围绕轨道以环形布置观测点。观测点坐标分别为:A(350,0,0)、B(100,0,0)、C(200,50,0)、D(400,100,0)、E(600,0,0)、F(400,-100,0)、G(200,-50,0)。在列车制动时牵引电流发生突变,记录此时各观测点地电位的TDOA数据,分别为:B点,1.948 885 μs;C点,0.790 961 μs;D点,1.158 652 μs;E点,3.214 782 μs;F点,1.175 164 μs;G点,0.799 621 μs。
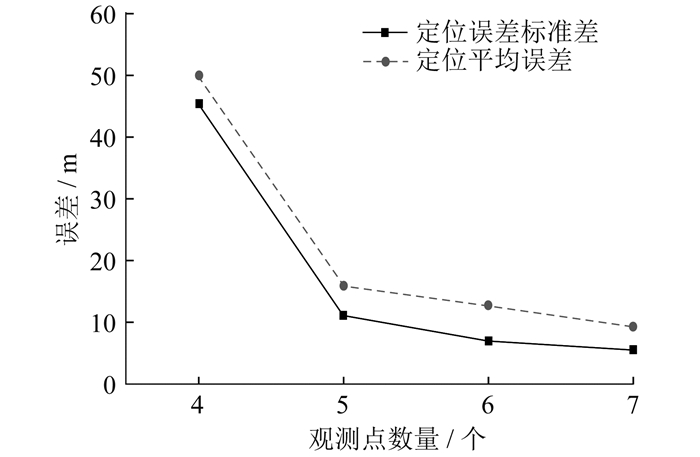
考虑到实际工程中存在测量误差,对测量值加入期望为0、方差为1的高斯噪声,模拟实际工作环境。经过10次仿真实验,计算出不同数量观测点下的定位平均误差。仿真中绝缘破损扣件的坐标为(300,1.4,-10),当观测点数量为4时,定位最大误差Δdmax=77.84 m,平均误差Δdavg=45.42 m;观测点数量为5时,Δdmax=16.84 m,Δdavg=11.13 m;观测点数量为6时,Δdmax=16.02 m,Δdavg=6.92 m;观测点数量为7时,Δdmax=10.33 m,Δdavg=5.59 m。不同观测点数量下TDOA定位误差情况如 图 8所示。
由图 8可知,观测点数量为4时采用TDOA原理定位误差较大,且定位受噪声干扰严重,定位结果离散度较大。增加探测点的数量并采用Chan算法定位能够有效提高定位的精度,同时降低定位离散度,有效提高定位抗噪声能力。当观测点增加到一定数量后,继续增加观测点对定位精度的提升幅度就变得很小。
5 结论
本文针对轨道交通钢轨扣件绝缘破损场景,分析了杂散电流侵入土壤的机理,建立了杂散电流动态仿真模型。利用地电位的时频特性,结合TDOA定位原理及Chan算法提出了一种对绝缘破损点的定位方法。通过仿真验证得到以下结论。
(1)轨道交通杂散电流的泄漏主要是由钢轨扣件绝缘破损造成的,杂散电流侵入土壤会导致轨道交通沿线的地电位提升,杂散电流的大小与流经钢轨的回流电流变化规律呈显著正相关,均表现为连续的冲击特征。
(2)钢轨扣件绝缘破损时,破损点附近地电位及地电位梯度会出现明显提升,显著超过安全标准。当线路上多列车同时启动时,其干扰范围可能超过1 000 m。
(3)设置地电位观测点,测量地电位波动的TDOA数据。根据本文所提算法能够实现对绝缘破损点的有效定位,定位精度和抗噪声能力随着观测点数量的增加而提高。当观测点数量为7时,定位最大误差为10.33 m,且能够有效过滤噪声影响。
参考文献
-
[1]史云涛, 赵丽平, 林圣, 等. 城市电网中地铁杂散电流分布规律及影响因素分析[J]. 电网技术, 2021, 45(5): 1951-1957.
-
[2]杜峰, 史文钊, 徐丽莉, 等. 城市轨道交通牵引供电系统综合平台设计与研究[J]. 上海电力大学学报, 2022, 38(4): 386-390.
-
[3]黄华, 陈璐, 吴天逸, 等. 城市轨道交通动态运行对交流电网变压器偏磁直流的影响[J]. 电网技术, 2022, 46(11): 4524-4533.
-
[4]DOLARA A, FOIADELLI F, LEVA S. Stray current effects mitigation in subway tunnels[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2304-2311. DOI:10.1109/TPWRD.2012.2203829
-
[5]LEE C H. Evaluation of the maximum potential rise in Taipei rail transit systems[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1379-1384. DOI:10.1109/TPWRD.2004.833902
-
[6]曹晓斌, 沈豪, 陶鑫. 地铁钢轨扣件对地过渡电阻等效电路及各部件的影响因素研究[J]. 高压电器, 2020, 56(8): 59-65.
-
[7]刘燕, 王京梅, 赵丽, 等. 地铁杂散电流分布的数学模型[J]. 工程数学学报, 2009, 26(4): 571-576.
-
[8]郑子璇, 杜贵府, 朱成乾. 城轨多区间绝缘非均匀情况下钢轨电位与杂散电流建模及分布[J]. 北京交通大学学报, 2020, 44(3): 66-78.
-
[9]LIN S, ZHOU Q, LIN X H, et al. Infinitesimal method based calculation of metro stray current in multiple power supply sections[J]. IEEE Access, 2020, 8: 96581-96591. DOI:10.1109/ACCESS.2020.2994125
-
[10]蔡智超, 程浩, 林知明. 考虑地铁车辆牵引因素下杂散电流的规律研究[J]. 电工电能新技术, 2018, 37(8): 82-88.
-
[11]穆永保, 闫柯柯, 岳国良, 等. 地铁杂散电流地电场影响因素关键性研究[J]. 西安科技大学学报, 2021, 41(6): 1122-1129.
-
[12]王禹桥, 黄玉坚, 彭成宽, 等. 基于地表电位梯度的地铁杂散电流动态干扰范围评估模型[J]. 北京交通大学学报, 2020, 44(3): 30-36.
-
[13]倪砚茹, 曾祥君, 喻锟, 等. 地铁杂散电流引起动态地电位分布建模及影响因素分析[J]. 中国电机工程学报, 2023, 43(23): 9059-9071.
-
[14]朱峰, 李嘉成, 曾海波, 等. 城市轨道交通轨地过渡电阻对杂散电流分布特性的影响[J]. 高电压技术, 2018, 44(8): 2738-2745.
-
[15]暴家良, 李晓华, 辛全金, 等. 城市轨道交通钢轨紧固件绝缘垫破损对杂散电流空间分布的影响[J]. 电工电能新技术, 2023, 42(7): 10-22.
-
[16]夏能弘, 唐文涛, 李怀慎, 等. 地铁轨道局部绝缘损坏下动态杂散电流及地电位梯度建模与分析[J]. 电力系统保护与控制, 2023, 51(4): 53-61.
-
[17]苏宁宁. 地铁轨道对地局部绝缘损坏点定位方法研究[D]. 徐州: 中国矿业大学, 2022.
-
[18]薛宏宇. 基于光纤光栅的地铁走行轨绝缘破损定位关键技术研究[D]. 徐州: 中国矿业大学, 2021.
-
[19]阎肖鹏, 张志伟, 王红萍. Chan算法在海上声源定位测量中的应用[J]. 声学技术, 2021, 40(4): 550-555.
-
[20]沈国清, 卢磊, 安连锁, 等. 基于Chan的残差加权算法在锅炉四管泄漏定位中的应用[J]. 热力发电, 2015, 44(11): 48-52.
-
[21]郑欣, 叶青, 赵文彬. 城市轨道交通用电负荷参数化建模方法及应用分析[J]. 城市轨道交通研究, 2022, 25(增刊1): 42-47.
-
[22]叶青, 赵文彬, 郑欣, 等. 城市轨道交通连续冲击负荷对主变压器热寿命影响研究[J]. 机车电传动, 2023(1): 122-130.