|
|
|
发布时间: 2024-06-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-12-18
基金项目: 教育部“春晖计划”合作科研项目(HZKY20220084);上海市自然科学基金(21ZR1425400);上海市青年科技启明星计划(21QC1400200)
中图法分类号: TM351
文献标识码: A
文章编号: 2096-8299(2024)03-0265-09
|
摘要
提出了一种新型双三相槽口永磁型混合励磁双凸极发电机,建立了该电机的矢量空间解耦数学模型,分析了不同工况下电机的电感特性,并提出了一种考虑电感变化的发电稳压铜耗监督控制策略。该策略建立了以最小铜耗为目标,以转矩、电流和电压为约束的非线性规划模型。首先,查找电感响应面,获得电机在当前工况下的实时电感参数;其次,将实时电感代入模型作二次优化,得到适用于电机当前工况的d轴、q轴优化电流及励磁优化电流,在实现系统稳压发电的同时有效减少铜耗;最后,通过Ansys和Simulink的联合仿真,验证所提控制策略的正确性和有效性。
关键词
双三相; 槽口永磁型混合励磁双凸极电机; 电感特性; 最小铜耗; 电流优化
Abstract
A new type of double three-phase slot PMs hybrid excitation doubly salient generator is proposed, and its vector space decoupling mathematical model is established. The inductance characteristics of the motor under different working conditions are analyzed, and a copper loss supervisory control strategy for voltage stabilization considering inductance variation is proposed. The strategy establishes a nonlinear programming model with the minimum copper loss as the objective and the torque, current and voltage as the constraints. Firstly, the real-time inductance parameters of the motor under the current working condition are obtained by searching the inductance response surface. Then the real-time inductance is substituted into the model for secondary optimization and the optimal current of d and q axis and excitation current suitable for the current working condition of the motor are obtained, which can ensure the stable voltage output of the system and effectively reduce the copper loss. Finally, the correctness and effectiveness of the proposed control strategy are verified by the co-simulation of Ansys and Simulink.
Key words
double three-phase; slot PMs hybrid excitation doubly salient motor; inductance characteristics; minimum copper loss; optimal current
为解决永磁双凸极电机的气隙磁场难以调节、应用范围受限等问题,电励磁双凸极电机(Doubly Salient Electro-magnet Motor,DSEM)和混合励磁双凸极电机(Hybrid Excitation Doubly Salient Motor,HEDSM)被先后提出。由于定子上增加了励磁绕组,DSEM和HEDSM可以通过控制励磁电流调节气隙磁场,有效扩展了电机发电状态下的调压范围和电动状态下的调速范围[1-6]。
目前,针对DSEM和HEDSM的高效率控制已有大量研究成果。文献[7-9]研究了DSEM电感周期变化特性,通过细化开关管的不同导通状态,充分利用电感变化的有效区域,提高了电机的输出功率。文献[10]对DSEM进行速度分区控制:中低速运行时,以一种同步换相控制实现改进方波电流的换相,增大了电机的转矩电流比;高速运行时,从旋转矢量角度分析电机模型并改进弱磁策略,提升了转矩输出能力。文献[11]结合矢量控制与速度分区控制原理,基于HEDSM提出了一种铜耗最小的弱磁调速策略,以铜耗最小为目标,在满足电压限制的条件下,自适应调节弱磁基速系数,对励磁和电枢电流进行优化以实现宽速弱磁控制。文献[12]提出了一种针对混合励磁磁通切换电机的最大转矩铜耗比控制策略,在低速区利用励磁电流提高带载能力,在高速区以电压、转矩、电流等为约束条件建立铜耗的目标函数,以实现转矩与铜耗的最大比。文献[13]对磁阻电机交直轴电感随电枢电流变化的现象进行探究,利用有限元分析得到电感与电流的对应关系,实现了不同电枢电流下的最大转矩电流比控制。文献[14]针对HEDSM提出了一种新的绕组控制策略,在低速范围内控制电枢绕组与励磁绕组串联连接,实现较大的启动转矩,而在高速范围内,向励磁绕组注入电流,实现电枢绕组的变速恒压。
增加电机相数能够进一步提高电机功率密度和容错能力,目前对多相电机控制策略的研究大多集中于双三相永磁同步电机(Permanent Magnetic Synchronous Motor,PMSM)。文献[15-16]建立了双三相PMSM不同坐标系下的矢量空间解耦控制模型,对比分析了矢量控制和直接转矩控制的特点。文献[17-18]研究了宽转速范围下PMSM的整流控制,通过建立小信号分析模型和脉冲宽度调制整流器的传递函数,优化了系统的控制参数,实现了PMSM系统的高性能稳压控制。
以上控制策略主要采用角位置控制或矢量控制作为基本控制。其中:角位置控制大多从电机电感周期变化的特性出发,对开通角和关断角进行优化,以充分利用电感自然上升和下降的过程,但在寻优过程中通常假设励磁电流恒定,未考虑不同稳压及调速要求下可变励磁电流与开通角、关断角的相互配合;矢量控制虽然从整体上对电机励磁电流和d轴、q轴电流进行了分配优化,能够有效扩展电机调速调压范围,但在其优化过程中电机的电感参数大多被认为恒定不变,与实际情况存在差异。
本文提出了一种新型双三相槽口永磁型混合励磁双凸极发电机(Slot PMs Hybrid Excitation Doubly Salient Generator,SP-HEDSG),在Maxwell中建立了该电机的本体模型,结合有限元仿真对不同工况下该电机的电感特性进行了理论分析。在此基础上,针对该电机电感参数变化幅度大的特征,提出了一种考虑电感变化的发电稳压铜耗监督控制(Copper Loss Supervision and Control,CLSC)策略。该策略建立了一个以铜耗最小为目标,以转矩、电流和电压为约束的非线性规划模型。首先,通过电感响应面获得电机的实时电感参数;其次,将实时电感代入非线性规划模型,对电机电枢电流和励磁电流进行二次优化,在实现系统稳压发电的同时,有效减少电机发电铜耗;最后,对该策略进行了仿真验证。
1 双三相SP-HEDSG的拓扑结构、电感特性及矢量空间解耦模型
1.1 电机拓扑结构
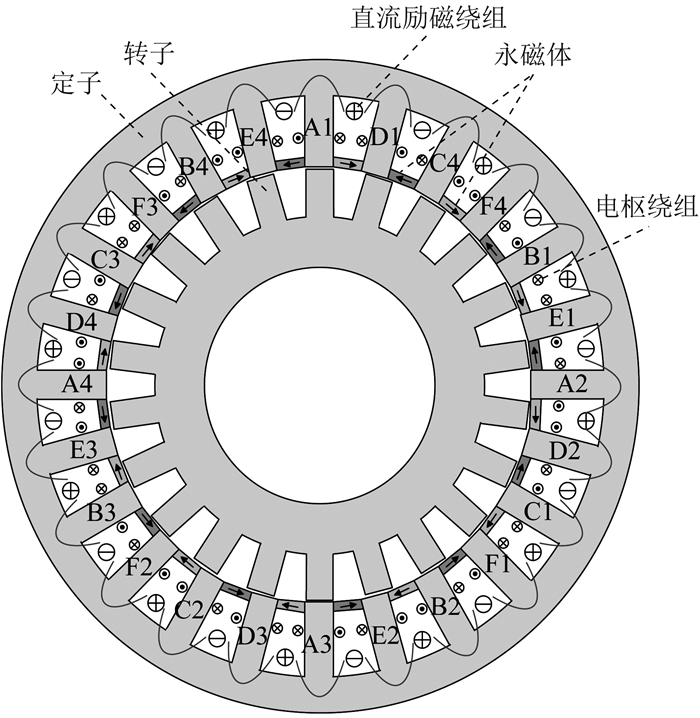
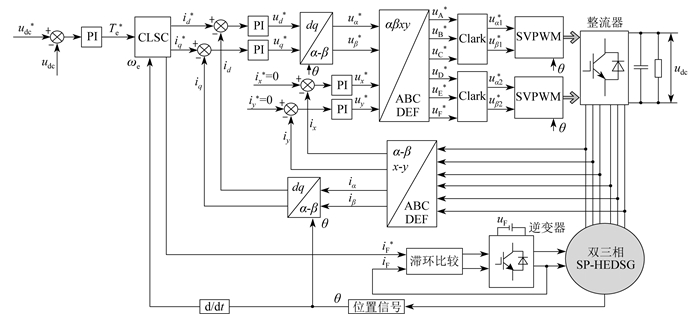
双三相SP-HEDSG的拓扑结构如图 1所示。定转子极数分别为24和22,定子上有直流励磁绕组、电枢绕组和永磁体。转子由硅钢片组成,结构简单,散热方便。直流励磁绕组依次绕制在每个定子极上。电枢绕组由ABC和DEF两套相同的Y形三相对称绕组组成,两套绕组互差30°且中性点隔离,各相电枢绕组(A1B1C1~A4B4C4,D1E1F1~D4E4F4)在定子极上的具体分布已在图 1中标出。永磁体放置于定子槽口,并进行切向充磁。双三相SP-HEDSG本体设计的进一步说明见增强出版附加材料。
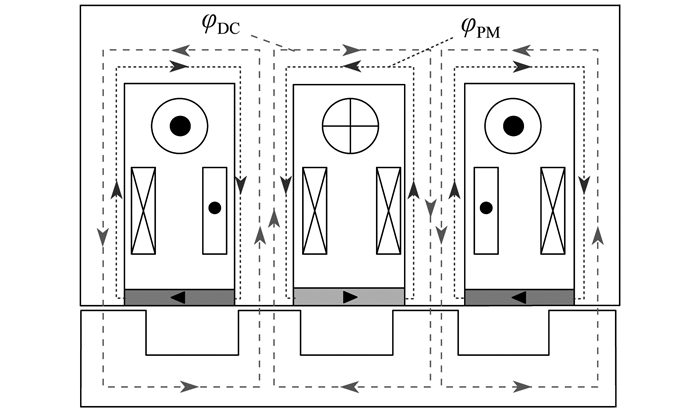
双三相SP-HEDSG的空载磁通分布如图 2所示。其中,励磁磁通ΦDC方向为顺时针,当转子旋转时,ΦDC呈单极性变化,存在直流偏置饱和[6];永磁磁通ΦPM方向为逆时针,当转子旋转时,ΦPM大小和方向几乎不变。通过调整ΦPM的大小可以使ΦDC的直流偏置分量下降为零,此时定子铁心利用率最高且电枢绕组的反电势也最大,能够有效提高电机的功率密度。
1.2 电感特性分析
获得精确的电机电感参数是合理设计电机控制策略的前提。对于以永磁体为主励磁的混合励磁电机,其正常运行时永磁部分磁路处于高度饱和状态,而电励磁部分饱和程度较低,因而d轴电感Ld和q轴电感Lq,以及励磁绕组与d轴的互感MdF在不同励磁电流下几乎不变[19-20]。但对于本文的双三相SP-HEDSG,其永磁体仅用于缓解励磁绕组的直流偏置饱和,主磁场由直流励磁绕组建立,故其d轴、q轴电感和互感MdF受到励磁电流的影响较大,需对其进行分析。
在双三相SP-HEDSG中,电感特性包括电枢绕组的电感特性及其与励磁绕组间的互感特性公式如下:
| $ \left\{\begin{array}{l} \boldsymbol{L}_{d q}=\boldsymbol{C}_{1} \boldsymbol{L}_{0} \boldsymbol{C}_{2} \\ \boldsymbol{M}_{d q}=\boldsymbol{C}_{1} \boldsymbol{M}_{0} \end{array}\right. $ | (1) |
| $ \boldsymbol{C}_1=\frac{1}{3}\left[\begin{array}{cccccc} \cos \theta & \cos \left(\theta-\frac{2 {\mathsf{π}}}{3}\right) & \cos \left(\theta-\frac{4 {\mathsf{π}}}{3}\right) & \cos \left(\theta-\frac{{\mathsf{π}}}{6}\right) & \cos \left(\theta-\frac{5 {\mathsf{π}}}{6}\right) & \cos \left(\theta-\frac{3 {\mathsf{π}}}{2}\right) \\ -\sin \theta & -\sin \left(\theta-\frac{2 {\mathsf{π}}}{3}\right) & -\sin \left(\theta-\frac{4 {\mathsf{π}}}{3}\right) & -\sin \left(\theta-\frac{{\mathsf{π}}}{6}\right) & -\sin \left(\theta-\frac{5 {\mathsf{π}}}{6}\right) & -\sin \left(\theta-\frac{3 {\mathsf{π}}}{2}\right) \end{array}\right] $ | (2) |
| $ \boldsymbol{C}_2=3 {\boldsymbol{C}_1}^{\mathrm{T}} $ | (3) |
| $ \boldsymbol{L}_0=\left[\begin{array}{cccccc} L_{11} & M_{12} & M_{13} & M_{14} & M_{15} & M_{16} \\ M_{12} & L_{22} & M_{23} & M_{24} & M_{25} & M_{26} \\ M_{13} & M_{23} & L_{33} & M_{34} & M_{35} & M_{36} \\ M_{14} & M_{24} & M_{34} & L_{44} & M_{45} & M_{46} \\ M_{15} & M_{25} & M_{35} & M_{45} & L_{55} & M_{56} \\ M_{16} & M_{26} & M_{36} & M_{46} & M_{56} & L_{66} \end{array}\right] $ | (4) |
| $ \boldsymbol{M}_0=\left[\begin{array}{l} M_{17} \\ M_{27} \\ M_{37} \\ M_{47} \\ M_{57} \\ M_{67} \end{array}\right] $ | (5) |
式中:Ldq——dq坐标系下电枢绕组的电感参数;
Mdq——dq坐标系下电枢绕组与励磁绕组之间的互感参数;
L0——静止坐标系下电枢绕组的电感参数,L11~L66为A相至F相的电枢绕组自感,Mab为两相之间的互感,a、b=1,2,3,4,5,6;
M0——静止坐标系下电枢绕组与励磁绕组之间的互感参数,下标7为励磁绕组;
θ——转子电角度。
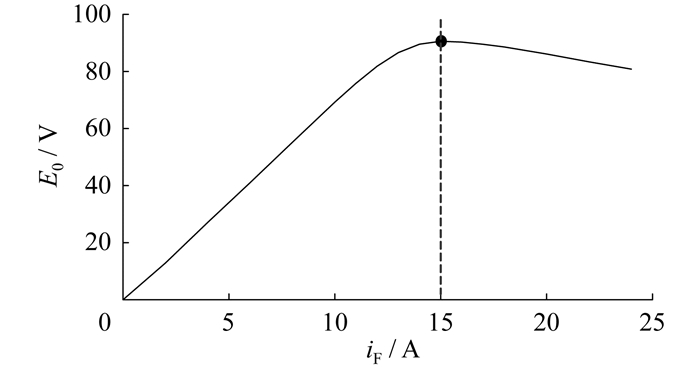
为了得到精确的电感参数,在Maxwell环境下进行电机本体建模。该电机在转速300 r/min下的空载特性曲线如图 3所示。当励磁电流iF为15 A时,空载电动势E0达到最大值。
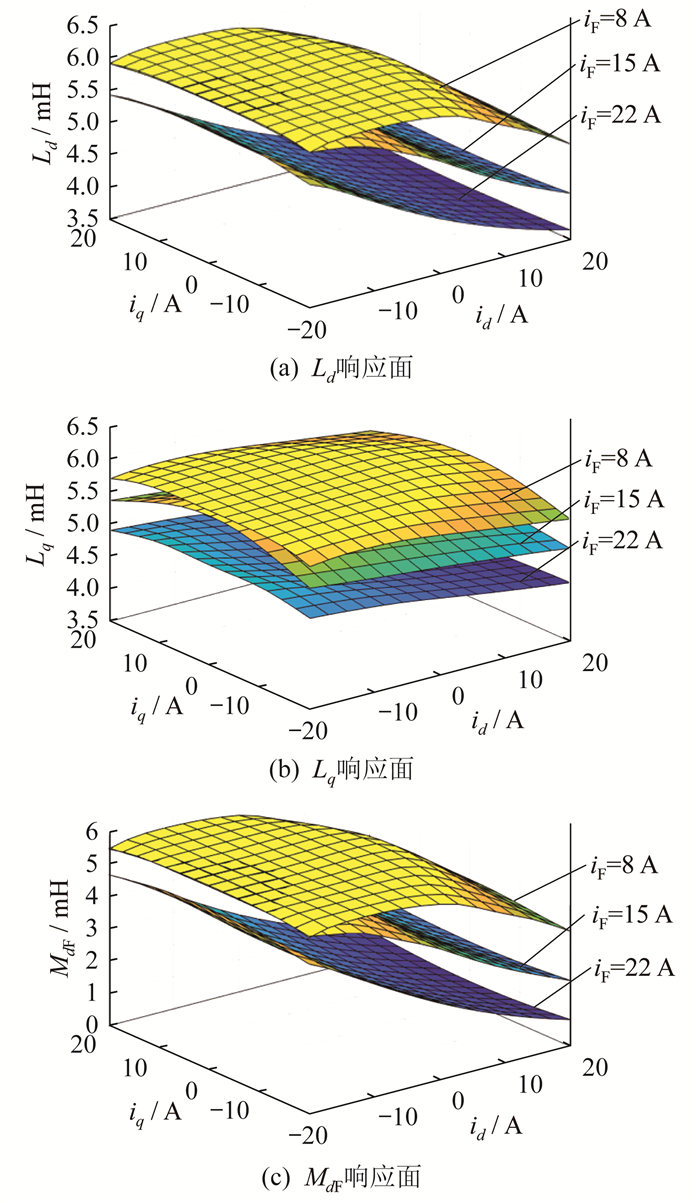
根据电机空载特性,选取励磁电流8、15、22 A作为电机工作在不饱和、饱和及深度饱和状态下的特征电流,结合有限元仿真得到不同饱和状态下d轴电感Ld、q轴电感Lq,以及MdF随d轴和q轴电流变化的响应面,如图 4所示。
当iF=8 A时,电机处于不饱和状态,Ld、Lq、MdF均主要受d轴电流id影响。此时,若id较小,则Ld、Lq、MdF近似恒定不变;当id较大时,即电机进入饱和状态,则Ld、Lq、MdF会随着id的增大而减小。当iF=15 A时,电机处于临界饱和状态,Ld和MdF主要受id影响,Lq由d轴电流id和q轴电流iq共同影响。此时,若id增大或iq的绝对值增大,等效于电机饱和程度加深,则Ld、Lq、MdF会随之减小。当励磁电流iF=22 A时,电机已处于深度饱和状态,此时Ld、Lq、MdF几乎只受id影响,且随着id的增大而减小。
整体上看,当id、iq、iF改变时,Ld和Lq都会随之发生变化。当iF恒定时,在相同的id和iq变化范围内,Ld的变化幅度明显大于Lq。这是由于d轴磁路穿过的等效气隙小于q轴磁路,相同工况下电机的d轴磁路更易受电流影响而饱和。
为了兼顾电机的使用效率和工作寿命,通常使其运行在饱和状态附近。本文限制iF∈[10 A,18 A],额定励磁电流iFN=15 A,对应的电感区间Ld∈[3.99 mH,6.03 mH]、Lq∈[4.81 mH,5.9 mH]、MdF∈[3.67 mH,4.92 mH],平均电感Ldm=5.32 mH、Lqm=5.43 mH、MdFm=4.63 mH。
1.3 矢量空间解耦数学模型
根据矢量空间解耦变换原理[15-16],电机分量可解耦至3个非耦合子平面。其中α-β平面的分量参与机电能量转换;x-y平面的分量虽不参与机电能量转换,但会产生谐波电流,以铜耗的形式转换为热量;o1-o2平面的分量均为零序分量,同样不参与机电能量转换,且由于中性点隔离,该平面上的电流始终为零,无需考虑谐波抑制。
对参与机电能量转换的α-β平面分量进行Park变换,可得到dq坐标系下的相关表达式。
磁链方程为
| $ \left\{\begin{array}{l} \psi_{d}=L_{d} i_{d}+M_{d {\rm{F}}} i_{\mathrm{F}}+\psi_{\mathrm{pm}} \\ \psi_{q}=L_{q} i_{q} \end{array}\right. $ | (6) |
式中:ψd,ψq——d轴磁链和q轴磁链;
ψpm——永磁磁链。
电压方程为
| $ \left\{\begin{array}{l} u_{d}=R_{\mathrm{s}} i_{d}+\frac{\mathrm{d} \psi_{d}}{\mathrm{d} t}-\omega_{\mathrm{e}} \psi_{q} \\ u_{q}=R_{\mathrm{s}} i_{q}+\frac{\mathrm{d} \psi_{q}}{\mathrm{d} t}+\omega_{\mathrm{e}} \psi_{d} \end{array}\right. $ | (7) |
式中:ud,uq——d轴电压和q轴电压;
Rs——单相电枢绕组电阻;
ωe——电机转速。
转矩方程为
| $ T_{\mathrm{e}}=3 P_{\mathrm{r}} i_{q}\left[\psi_{\mathrm{pm}}+M_{d \mathrm{F}} i_{\mathrm{F}}+\left(L_{d}-L_{q}\right) i_{d}\right] $ | (8) |
式中:Pr——转子极对数。
电机铜耗包括α-β平面和x-y平面上的铜耗和励磁铜耗,总铜耗PCu为
| $ P_{\mathrm{Cu}}=3 R_{\mathrm{s}}\left(i_{d}^{2}+i_{q}^{2}\right)+R_{\mathrm{F}} i_{\mathrm{F}}^{2}+3 R_{\mathrm{s}}\left(i_{x}^{2}+i_{y}^{2}\right) $ | (9) |
式中:RF——励磁绕组电阻;
ix,iy——x轴电流和y轴电流。
当电机稳定运行时,ix和iy的值接近于零,占总铜耗的比重极小,因此可以忽略ix和iy,则式(9)可简化为
| $ P_{\mathrm{Cu}}=3 R_{\mathrm{s}}\left(i_{d}^{2}+i_{q}^{2}\right)+R_{\mathrm{F}} i_{\mathrm{F}}^{2} $ | (10) |
2 考虑电感变化的CLSC策略
2.1 CLSC策略初步优化
受全桥变换器容量及散热限制,电机电流和电压的限值分别为
| $ i_{d}^{2}+i_{q}^{2} \leqslant i_{\max }^{2} $ | (11) |
| $ u_{d}^{2}+u_{q}^{2} \leqslant u_{\max }^{2}=\left(u_{\mathrm{dc}} / \sqrt{3}\right)^{2} $ | (12) |
式中:imax——电流极限;
umax——电压极限;
udc——变换器直流侧母线电压。
将式(7)代入式(12),当电机稳定运行且忽略电阻压降时,式(12)可改写为
| $ \left(-L_{q} i_{q}\right)^{2}+\left(\psi_{\mathrm{pm}}+L_{d} i_{d}+M_{d \mathrm{F}} i_{\mathrm{F}}\right)^{2} \leqslant\left(\frac{u_{\mathrm{dc}}}{\sqrt{3} \omega_{\mathrm{e}}}\right)^{2} $ | (13) |
针对传统速度分区控制策略存在的问题,CLSC策略在电机全速域内建立了一个以铜耗方程为目标函数,转矩方程为等式约束,电流和电压限值方程为不等式约束的非线性规划模型。该模型不仅利用了非弱磁区的磁阻转矩,而且在电机全速域内考虑了d轴、q轴电流和励磁电流的优化分配。模型如下:
| $ \left\{ \begin{array}{l} 目标函数:\min \left(P_{\mathrm{Cu}}\right)=\min \left[3 R_{\mathrm{s}}\left(i_{q}^{2}+i_{d}^{2}\right)+R_{\mathrm{F}} i_{\mathrm{F}}^{2}\right]\\ 转矩约束: T_{\mathrm{e}}=3 P_{\mathrm{r}} i_{q}\left[\psi_{\mathrm{pm}}+\left(L_{d}-L_{q}\right) i_{d}+M_{d \mathrm{F}} i_{\mathrm{F}}\right]\\ 电流约束: i_{q}^{2}+i_{d}^{2} \leqslant i_{\text {max }}^{2}\\ 电压约束: \left(-L_{q} i_{q}\right)^{2}+\left(\psi_{\mathrm{pm}}+L_{d} i_{d}+M_{d \mathrm{F}} i_{\mathrm{F}}\right)^{2} \leqslant\left(\frac{u_{\mathrm{dc}}}{\sqrt{3} \omega_{\mathrm{e}}}\right)^{2} \end{array} \right. $ | (14) |
在上述模型中,对于任意一个转矩Te,会有无数组id、iq、iF的组合满足约束,且存在一组最优电流能够使得电机发电铜耗最小,定义该组最优电流为CLSC初步优化电流。将不同工况下的初步优化电流存入查找表,在实际控制中就可以根据电机实时工况查表得到对应的初步优化电流。
CLSC策略下双三相SP-HEDSG的矢量控制系统如图 5所示。给定电压udc*和输出电压udc的差值经PI控制得到给定转矩Te*,将Te*和转速ωe输入CLSC策略,查表得到优化电流id*、iq*、iF*。其中,id*和iq*分别与id和iq作差,经PI控制得ud*和uq*,再经Park逆变换得到uα*、uβ*。为有效抑制x-y平面谐波电流,同样用PI控制对ix和iy进行零参考值的闭环控制,可得ux*和uy*。将uα*、uβ*、ux*、uy*作解耦逆变换,可得双三相绕组的给定电压uA*~uF*,再对ABC和DEF两套绕组各自进行Clark变换可得对应的参考电压uα1*、uα2*、uβ1*、uβ2*,最后通过空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)实现对整流器的控制。优化励磁电流iF*与励磁电流iF经滞环比较后,通过单相全桥电路实现控制。
2.2 CLSC策略二次优化
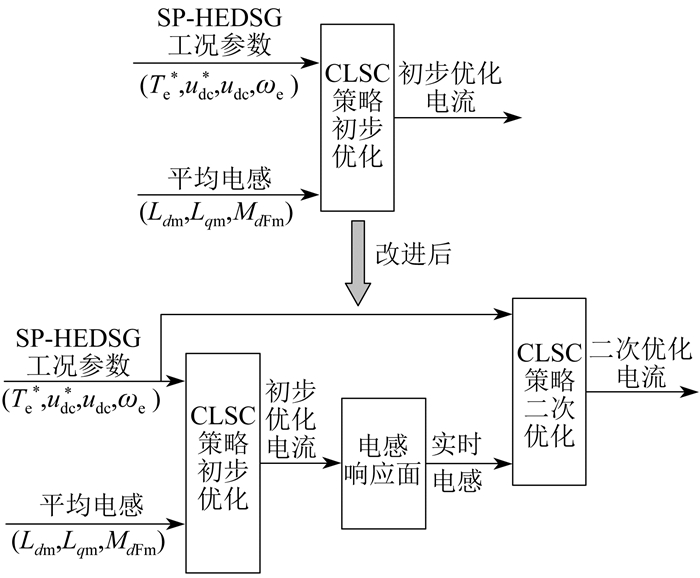
CLSC初步优化电流是根据d轴和q轴的平均电感求解得到。但当电机在不同的优化电流下工作时,d轴、q轴的实时电感与平均电感存在差值。为了得到更适用于实际工况的优化电流,本文在CLSC初步优化的基础上进行了二次优化。首先,根据CLSC初步优化电流查找电感响应面,得到初步优化电流对应的实时d轴和q轴电感;然后,利用实时电感代替平均电感,并对非线性规划模型进行第二次求解,得到CLSC二次优化电流。改进前后的优化电流对比如图 6所示。
3 基于ANSYS和Simulink的联合仿真
3.1 联合仿真模型
本文对双三相SP-HEDSG系统建立了基于ANSYS和Simulink的联合仿真模型。在ANSYS中搭建电机本体模型和全桥控制电路,全桥开关管的控制信号则由Simulink得到。
给定目标电压udc*=75 V,负载R=10 Ω,电机的主要参数如表 1所示。其中,该电机将直流励磁磁链方向定义为正方向,而永磁磁链方向与直流磁链方向相反,故其磁链幅值为负值。
表 1
双三相SP-HEDSG主要参数
| 参数 | 数值 |
| 电枢绕组电阻/ft | 0.53 |
| 励磁绕组电阻/ft | 1.26 |
| 直轴电感(平均值)/mH | 5.32 |
| 交轴电感(平均值)/mH | 5.43 |
| 励磁与电枢绕组互感(平均值)/mH | 4.63 |
| 永磁磁链幅值/Wb | -0.001 2 |
| 额定转速/(r/min) | 250 |
| 额定励磁电流/A | 15 |
| 励磁电流范围/A | [10, 18] |
由以上条件,可计算得到传统控制策略下该电机的两个弱磁基速n1=262.9 r/min,n2=321.3 r/min。由此选取转速240、290、500 r/min分别作为非弱磁区、弱磁1区和弱磁2区的测试转速,以对比传统控制策略和CLSC策略的控制效果。仿真模型的搭建及验证过程,见增强出版附加材料。
3.2 非弱磁区仿真结果分析
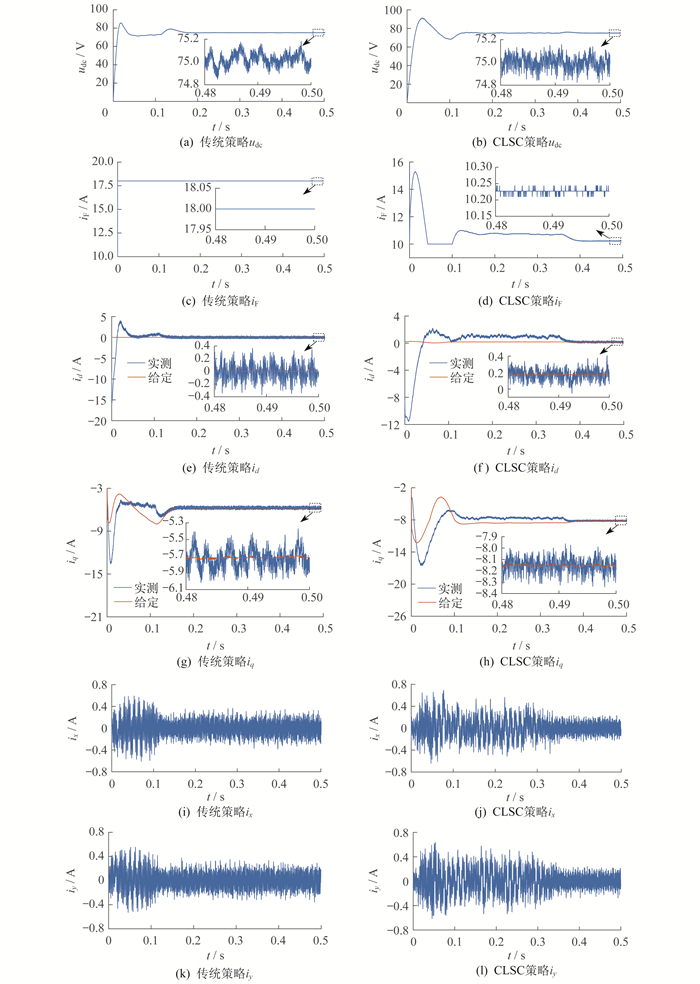
转速240 r/min下两种策略的仿真结果见图 7。
由图 7可以看出,两系统在0.4 s内均达到平衡状态,输出电压能够稳定于给定电压75 V。传统控制策略的优化电流iF*、id*、iq*分别为18.0、0、-5.7 A,实际电流能够跟随给定电流,对应铜耗为460.3 W;CLSC策略的iF*、id*、iq*分别为10.2、0.2、−8.2 A,实际电流同样能跟随给定电流,对应铜耗为237.5 W,相比传统控制策略铜耗减少了48.4 %。
此外,在电机稳定后两种策略下的x-y平面谐波电流平均值均小于0.2 A,对应产生的铜耗小于0.2 W,占总铜耗的比重极小,故前文总铜耗方程式(9)中可忽略ix和iy。
3.3 弱磁1区仿真结果分析
3.4 弱磁2区仿真结果分析
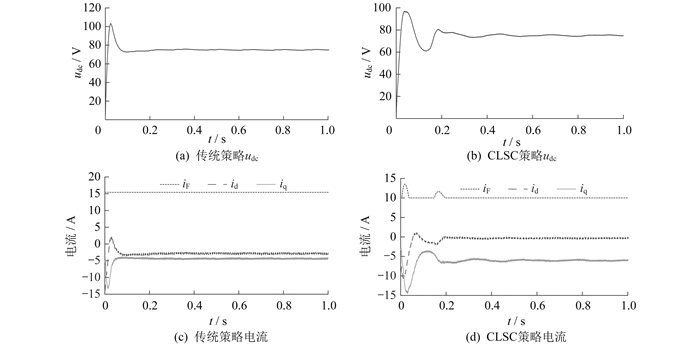
转速500 r/min下两种策略的仿真结果如图 9所示。
由图 9可以看出,两系统在0.6 s内均达到平衡状态,输出电压能够稳定于75 V。传统控制策略下iF、id、iq分别为10.0、-4.5、-3.5 A,对应铜耗为176.8 W;CLSC策略下iF、id、iq分别为10.0、-4.2、-3.3 A,对应铜耗为155.7 W,相比传统控制策略铜耗减少了11.9%,优化幅度相比240 r/min和290 r/min时较小。这是因为在当前转速下,两种策略给出的优化励磁电流均已达到下限(10 A),仅在d轴和q轴给定电流上有较小差距,因而最后的铜耗差距较小。
以上结果表明,两种控制策略在电机全速域内均能实现双三相SP-HEDSG系统的发电稳压控制,且本文所提的CLSC策略在减少铜耗方面相比传统控制策略具有明显优势。
4 结语
本文研究了一种新型双三相槽口永磁型混合励磁双凸极电机,对该电机不同工况下的电感特性进行了分析,结果表明,双三相SP-HEDSG的电感特性参数会随电机电枢电流和励磁电流的改变发生较大变化。此外,针对该电机电感参数变化幅度大的特征,本文提出了一种考虑电感变化的发电稳压铜耗监督控制策略,该策略以电流矢量控制为基础,通过查找电感响应面获得电机的实时电感参数,并根据实时电感对电机电枢电流和励磁电流进行优化分配。仿真结果表明,所提策略能够在保证双三相SP-HEDSG系统稳压输出的同时,有效减少电机的发电铜耗。
参考文献
-
[1]XU Y W, ZHANG Z R, BIAN Z M, et al. Copper loss optimization based on bidirectional converter for doubly salient brushless starter/generator system[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4769-4779. DOI:10.1109/TIE.2020.2988239
-
[2]CAI S, WANG Y, CHEN H, et al. Design and analysis of a doubly salient wound field starter generator for costeffective automobile application[J]. IEEE Transactions on Vehicular Technology, 2022, 71(7): 6900-6911. DOI:10.1109/TVT.2022.3163403
-
[3]程明, 张淦, 花为. 定子永磁型无刷电机系统及其关键技术综述[J]. 中国电机工程学报, 2014, 34(29): 5204-5220.
-
[4]SUN L N, ZHANG Z R, GU X P, et al. Analysis of a hybrid excitation brushless dc generator with an integrated shared-flux-path exciter[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 6672-6681. DOI:10.1109/TIE.2020.3001842
-
[5]XU Y W, ZHANG Z R, BIAN Z M, et al. Dynamic performance improvement of doubly salient brushless dc generator system with controlled rectifier[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8209-8218. DOI:10.1109/TIE.2019.2949536
-
[6]赵耀, 滕登晖, 李东东, 等. 四相容错型缓解直流偏置饱和的混合励磁磁阻发电机电磁特性研究[J]. 中国电机工程学报, 2022, 42(18): 6880-6892.
-
[7]刘星, 陈志辉, 朱杰, 等. 电励磁双凸极电动机三相六拍控制策略研究[J]. 中国电机工程学报, 2013, 33(12): 138-144.
-
[8]王寅, 张卓然, 袁琬欣, 等. 双凸极无刷直流电机三相九状态控制策略研究[J]. 中国电机工程学报, 2016, 36(10): 2808-2815.
-
[9]CHEN L, XU Y W, DING S Y, et al. Output performance model and three-phase nine-state control for doubly salient electromagnetic generator[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 16022-16033. DOI:10.1109/TPEL.2023.3318355
-
[10]卞张铭. 电励磁双凸极电机宽速域运行电流控制技术研究[D]. 南京: 南京航空航天大学, 2020.
-
[11]林鹤云, 黄明明, 陆婋泉, 等. 混合励磁同步电机铜耗最小化弱磁调速控制研究[J]. 中国电机工程学报, 2014, 34(6): 889-896.
-
[12]李帅, 丁文, 李可. 基于组合算法的混合励磁磁通切换电机最大转矩铜耗比控制[J]. 电工技术学报, 2022, 37(7): 1654-1665.
-
[13]袁赛赛, 蔡顺, 贺小克, 等. 同步磁阻电机最大转矩电流比矢量控制[J]. 微电机, 2017, 50(4): 43-46.
-
[14]JIANG J F, NIU S X, ZHAO X, et al. A novel winding switching control strategy of a consequent-pole ferrite-pm hybrid-excited machine for electric vehicle application[J]. IEEE Transactions on Magnetics, 2022, 58(2): 8700205.
-
[15]王学庆, 王政, 程明. T型三电平逆变器馈电双三相PMSM直接转矩控制[J]. 电工技术学报, 2017, 32(增刊1): 116-123.
-
[16]WANG Z, WANG X Q, YANG X J, et al. Mitigation of DC-link current ripple for dual three-phase flux-adjustable hybrid PMAC drives using collaborative switching strategy[J]. IEEE Transactions on Industrial Electronics, 2020, 67(9): 7202-7216. DOI:10.1109/TIE.2019.2945213
-
[17]邱建琪, 吴翊铭, 史涔溦. 基于多目标FCS-MPC的永磁同步发电机MTPA控制[J]. 轻工机械, 2021, 39(6): 50-56.
-
[18]甘志伟, 缪冬敏, 王云冲, 等. 宽转速范围永磁同步发电机系统稳压控制及参数优化[J]. 电工技术学报, 2020, 35(8): 1624-1633.
-
[19]WANG Y, DENG Z Q. Hybrid excitation topologies and control strategies of stator permanent magnet machines for dc power system[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4601-4616. DOI:10.1109/TIE.2012.2183842
-
[20]朱婷婷, 邓智泉, 王宇. 并列式混合励磁磁通切换型电机及其电流矢量控制策略研究[J]. 中国电机工程学报, 2012, 32(15): 140-147.