2021年发布的《世界能源蓝皮书：世界能源发展报告》指出^[1]，到2050年，可再生能源将满足全球80% 的电力需求，其中太阳能和风力发电将占52%。新能源发电比例增加和电力系统建设加剧了电源与用户之间的供需平衡矛盾。因此，将灵活的需求侧负载资源纳入电网运行已成为推动电力系统安全、有效和经济运行的重要方法。

需求侧柔性负荷资源是区域网络中广泛分布的高价值配电资源，电动汽车、温控负荷和分布式储能等资源的有效灵活调度，可以很大程度上缓解新能源接入对电力系统的冲击^[2]。电力需求响应作为重要的电力调度手段，可以推动电力系统稳定可靠运行，减少负荷压力，提高能源效率。文献[3]证明了需求响应技术促进间歇性可再生能源消费的可行性，但存在一定的局限性。文献[4-5]在爱尔兰电力系统中引入需求响应模型，证明了部分传统发电可被需求响应取代，大规模部署需求响应项目的关键是评估需求响应的灵活性和合理性。

作为新型交易市场的参与者，负荷聚合商将具有调节能力的需求侧资源聚合起来，成为沟通需求侧消费者和电力市场之间的桥梁^[6]。负荷聚合商不仅可与供电方共同参与各类电力市场交易，在获取自身经济利益的同时提高社会公共效益，还可与消费者达成代理合同，使运营利益和用电效益最大化^[7]。电动汽车-充电桩负荷是目前数量最多、应用最为广泛的需求侧柔性负荷资源。

建立电动汽车充电负荷模型最常用的方法是蒙特卡洛方法^[8]。在针对电动汽车有序充放电的研究中，文献[9]使用启发式算法对电力系统网络进行建模，以投入和能源消耗量最小为目标，制定了合理的控制策略。文献[10-11]运用粒子群算法得出1日内最佳充放电时间，提出了一种以减少峰谷差为目标的优化充电策略，减少了峰谷负荷差。在上述研究基础上，本文通过建立负荷参与需求响应调节模型和聚合调节模型，从园区负荷聚合商的视角，优化负荷侧资源参与需求响应的市场行为。

电池荷电状态(State of Charge，SOC)是计算电动汽车充电和放电的最关键参数。当电动汽车在t时段以指定功率充放电时，t时段电池SOC变化公式为

$ \begin{equation*} \frac{\mathrm{d} S_{\mathrm{OC}, \mathrm{EV}}^{t}}{\mathrm{~d} t}=s_{\mathrm{EV}}^{t} P_{\mathrm{EV}}^{t} \frac{\eta_{\mathrm{EV}}}{C_{\mathrm{EV}}} \end{equation*} $

(1)

式中：$ S_{\mathrm{OC}, \mathrm{EV}}^{t}$——t时段电动汽车电池SOC；

s_EV^t——t时段电动汽车电池充放电状态；

P_EV^t——t时段电动汽车电池充放电功率，kW；

C_EV——电动汽车电池容量，kWh；

η_EV——电动汽车电池充放电效率，%。

电池SOC和容量是计算并网电动汽车可调充电功率的关键参数，而电动汽车的日行驶里程直接影响电池SOC。因此，假设在电动汽车运行过程中，电池电量匀速下降，则电动汽车电池SOC与其行驶距离间的关系为

$ \begin{equation*} S_{\mathrm{OC}, \mathrm{EV}}^{t_{\mathrm{Land}} j+1}=S_{\mathrm{OC}, \mathrm{EV}}^{t_{\mathrm{OO}}, j}-(d / D) \times 100 \% \end{equation*} $

(2)

式中：$ S_{\mathrm{OC}, \mathrm{EV}}^{t_{\mathrm{Land}} j+1}$——j+1时段电动汽车初始SOC，%；

$ S_{\mathrm{OC}, \mathrm{EV}}^{t_{\mathrm{OO}}, j}$——j时段电动汽车充电后SOC，%；

d——j、j+1时段电动汽车行驶里程，km；

D——电动汽车额定续航里程，km。

根据美国交通部2009年对全美车辆出行情况调查结果可知，电动汽车接入电网时间的概率密度函数f_x(t_start)符合正态分布^[12]，公式为

$ \begin{equation*} f_{x}\left(t_{\text {start }}\right)=\frac{1}{\sigma_{\text {start }} \sqrt{2 \pi}} \exp \left[-\frac{\left(t_{\text {start }}-\mu_{\text {start }}\right)^{2}}{2 \sigma_{\text {start }}^{2}}\right] \end{equation*} $

(3)

式中：t_start——电动汽车充电起始时间；

σ_start，σ_start²——充电起始时刻及其方差；

μ_start——充电起始时刻均值。

电动汽车电池SOC满足的约束条件为

$\begin{equation*} S_{\mathrm{EV}, \text { min }} \leqslant S_{\mathrm{OC}, \mathrm{EV}}^{t} \leqslant S_{\mathrm{EV}, \text { max }} \end{equation*} $

(4)

式中：S_EV，min，S_EV，max——电动汽车电池SOC最小值和最大值。

式(1)至式(4)构成了电动汽车充放电模型。

首先，基于蒙特卡洛方法，按照概率密度随机抽取电动汽车电池容量、行驶里程、初始时刻电池SOC等参数。

然后，结合电动汽车允许的放电下限、离开时电量期望值、充电桩充放电模式等设定，建立电动汽车聚合负荷模型，以聚集区域内的电动汽车并参与电力市场需求响应。

同时，制定相应优化调节策略，激励电动汽车在非高峰时段充电，并在高峰时段通过电动汽车入网技术(Vehicle-to-Grid，V2G)转移其充电功率，供虚拟储能系统使用，使电动汽车既可作为系统负载，也可作为储能和分布式电源，从而减轻电网高峰时段的负荷压力，减少电动汽车用户的充电成本。

对美国家庭出行情况的调查研究(National Household Travel Survey，NHTS)显示^[13]，私家电动汽车1天出行的可能性遵循对数正态分布。车辆1天出行可能行驶里程的概率密度函数f_m(R_d)为

$ \begin{equation*} f_{\mathrm{m}}\left(R_{\mathrm{d}}\right)=\frac{1}{\sqrt{2 \pi} \sigma_{\mathrm{m}} R_{\mathrm{d}}} \exp \left[\frac{\left(\operatorname{In} R_{\mathrm{d}}-\mu_{\mathrm{m}}\right)^{2}}{2 \sigma_{\mathrm{m}}^{2}}\right] \end{equation*} $

(5)

式中：R_d——电动汽车日行驶里程数，可通过蒙特卡洛方法抽样得到概率密度和概率分布；

σ_m——固定参数，取0.87；

μ_m——固定参数，取3.31。

为确定电动汽车并网后的电池初始SOC，对包括电动汽车出行前的电池SOC、容量、能耗等参数进行抽样整理，得到公式为

$ \begin{equation*} S_{\mathrm{s}}=\delta-\frac{d_{\mathrm{r}} C_{\mathrm{e}}}{C_{\mathrm{EV}}} \end{equation*} $

(6)

式中：S_s——入网时电池初始SOC，%；

δ——用户出行前电池SOC值，%；

d_r——电动汽车日出行距离，km；

C_e——每公里电池能耗，kWh/km。

为了激励电动汽车参与需求响应，对电动汽车的实际调节和由于频繁充放电导致的电池损伤进行额外补偿，其充电调节成本C_ch为

$ C_{\mathrm{ch}}=\sum\limits_{i=1}^{N} \sum\limits_{i=1}^{n_{\mathrm{EV}}} p_{\mathrm{b}} s_{\mathrm{EV }, \mathrm{cha}}(i, t)\left[P_{\max }(i)-P_{\mathrm{EV}}(i, t)\right] \Delta t $

(7)

式中：n_EV——电动汽车数量；

N——电动汽车充电次数；

p_b——电网对参与调节后充电功率的补贴电费，元/kW；

s_EV，cha(i，t)——开关状态系数，表示电动汽车充电状态；

P_max(i)——第i辆电动汽车的最大充电功率，kW；

P_EV(i，t)——t时段第i辆电动汽车的实际充电功率，kW；

Δt——相邻两次充电的间隔时间。

电动汽车放电的储能成本P_disc^[7]和放电补贴成本C_disc为

$ \begin{gather*} P_{\text {disc }}=\frac{C_{\mathrm{EV}}}{N_{\mathrm{EV}}}+p_{\mathrm{b}} \end{gather*} $

(8)

$C_{\text {disc }}=\sum\limits_{t=1}^{N} \sum\limits_{i=1}^{N} p_{\text {disc }}^{n_{\mathrm{EV}}} S_{\mathrm{EV}, \text { disc }}(i, t) \frac{1}{\eta_{\text {disc }}} P_{\mathrm{EV}, \text { disc }}(i, t) \Delta t $

(9)

式中：C_EV——电动汽车电池成本，元/kWh；

N_EV——工作寿命内电动汽车的可充放电次数；

s_EV，disc(i，t)——开关状态系数，表示电动汽车放电状态；

P_EV，disc(i，t)——t时段第i辆电动汽车的放电功率，kW；

η_disc——放电效率。

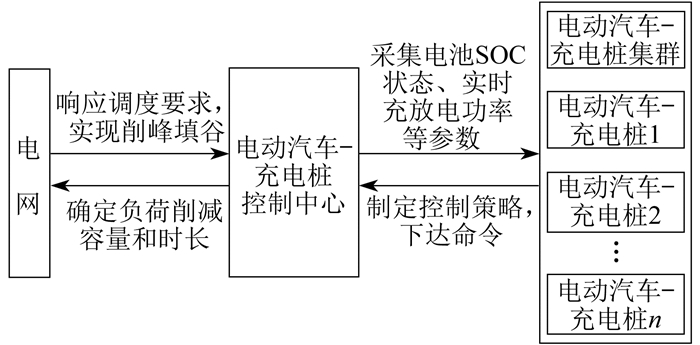
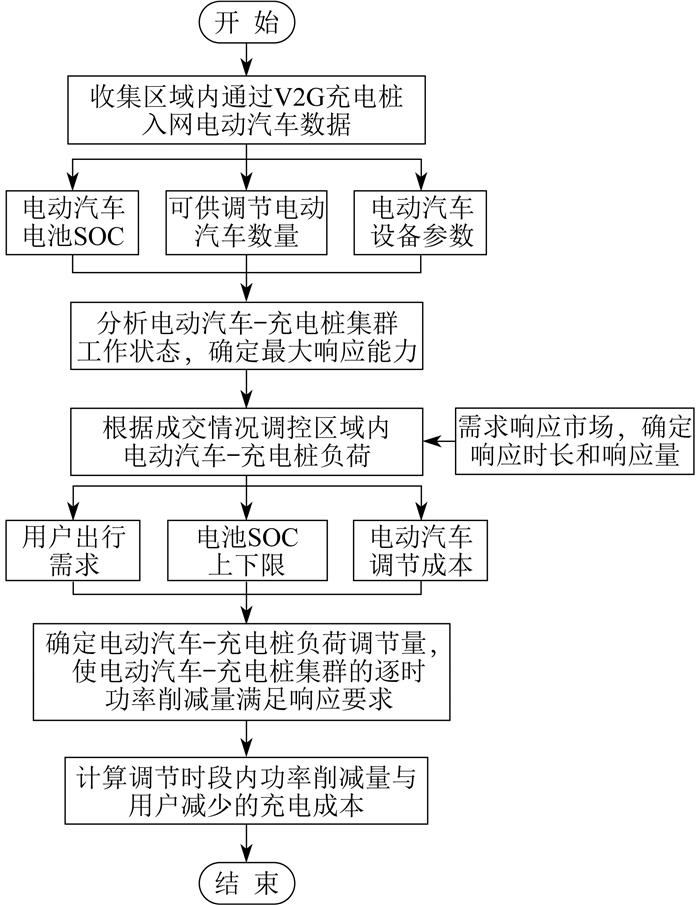
电动汽车-充电桩负荷优化实施框架如图 1所示。

电动汽车-充电桩调节策略如图 2所示。

由图 1和图 2可知，负荷聚合商综合考虑区域内通过V2G充电桩入网电动汽车电池SOC和需求响应要求，以及用户结束充电后的出行需求、电动汽车电池的状态上下限约束条件和电动汽车调节成本，确定电动汽车-充电桩负荷调节量，在保证实时功率削减量不少于要求的前提下，使负荷聚合商调节电动汽车-充电桩负荷参与需求响应的收益最佳。

在满足规定负荷削减量前提下，以负荷聚合商经济性最优为目标，对包含n辆电动汽车和n个充电桩的电动汽车群进行需求响应控制。在实现用户充电目标的前提下，通过有序充电、V2G反向向电网输电等措施，使用户通过V2G充电桩进行充电所产生的费用与电网对电动汽车反向供电的激励收益之差最小，其目标函数f_min为

$ f_{\min }=\min \left[\sum\limits_{i=1}^{n} \sum\limits_{t=1}^{T} P(i, t) p_{1}(t)-\sum\limits_{i=1}^{n} \sum\limits_{t=1}^{T} P_{\mathrm{dis}}(i, t) p_{2}(t)\right] $

(10)

式中：T——充电总时间；

P(i，t)——t时段第i辆电动汽车充电功率，kW；

p₁(t)——t时段通过充电桩充电电价，元/kW；

P_dis(i，t)——t时段第i辆电动汽车向电网反向放电功率，kW；

p₂(t)——电网对电动汽车反向供电激励价格，元/kW。

电动汽车电池SOC的约束条件为

$ S(i, t)=S(i, 0)+\eta_{\text {cha }} \sum\limits_{t=1}^{N} x_{\mathrm{EV}, \text { cha }}(i, t) P_{\mathrm{EV}, \text { cha }}(i, t) \Delta t- \\ \frac{1}{\eta_{\text {disc }}} \sum\limits_{t=1}^{N} x_{\mathrm{EV}, \text { disc }}(i, t) P_{\mathrm{EV}, \text { disc }}(i, t) \Delta t $

(11)

$S_{\text {min }} \leqslant S(i, t) \leqslant S_{\max } $

(12)

式中：S(i，0)，S(i，t)——初始时刻和t时段电动汽车电量，kW；

x_EV，cha(i，t)，x_EV，disc(i，t)——t时段第i辆电动汽车的充电状态变量和放电状态变量；

η_cha——充电效率；

P_EV，cha(i，t)——t时段第i辆电动汽车的充电功率，kW；

S_min，S_max——电池容量最小限制和最大限制。电动汽车可调节时间t(i) 为电动汽车与电网连接的时间，其约束条件为

$ \begin{equation*} t_{\text {start }}(i) \leqslant t(i) \leqslant t_{\text {end }}(i) \end{equation*} $

(13)

式中：t_start(i)，t_end(i)——第i辆电动汽车调节的开始时刻和终止时刻。

电动汽车离开时应满足车主所希望达到的电池SOC值为

$\begin{equation*} S_{\text {end }}(i) \geqslant S_{\text {set }}(i) \end{equation*} $

(14)

式中：S_end(i)，S_set(i)——第i辆电动汽车离开时实际电量和期望电量，kW。

相关研究将电动汽车状态简化为充电或放电两种^[14]，但电动汽车慢速充电6~7 h就能充满，因此本研究设定电动汽车状态为充电、放电和待机3种(即不充电或不放电)，且满足

$\begin{equation*} x_{\mathrm{cha}}+x_{\mathrm{disc}}+x_{\mathrm{sta}}=1 \end{equation*} $

(15)

式中：x_cha，x_disc，x_sta——电动汽车充电、放电和待机状态参数，0−1变量。

运用蒙特卡洛方法模拟的负荷聚合方法，通过概率密度对包括电动汽车电池容量、行驶里程、接入电网初始时刻的SOC等主要参数进行随机抽样，所有抽样模型的集合即为电动汽车充电桩负荷集群模型^[15]。

根据上文提出的电动汽车充电负荷聚合调节方法，以上海某大型工商业园区为例，建立电动汽车负荷聚合商聚合区域内电动汽车参与电力市场需求响应模型，制定聚合调节区域内电动汽车集群参与电力系统需求响应的优化调节策略。假设园区内配备V2G智能充电桩1 000个，其中30%是最大充放电效率为60 kW的快充充电桩，其余为最大充放电效率为7 kW的普通充电桩，充放电效率均为90%；对应1 000辆电池容量最大值为62.5 kW的电动汽车，初始时刻电量在20%~50%之间随机分布；电动汽车离开时S_set(i)为80%，设定仿真过程中电池SOC允许放电下限为20%，其余参数由蒙特卡洛方法抽样确定。设定仿真过程中，电动汽车接受调节时段为09：00—17：00，负荷聚合商对用户的放电补贴成本价格为2.5元/kWh。其中，在09：00—11：00和13：00—15：00时段，电动汽车通过智能充电桩充电的费用为2.6元/kWh，在11：00—13：00和15：00—17：00时段，充电费用为1.15元/kWh，要求园区内电动汽车在13：00—15：00时段内实现平均不少于6 MW的负荷削减量。

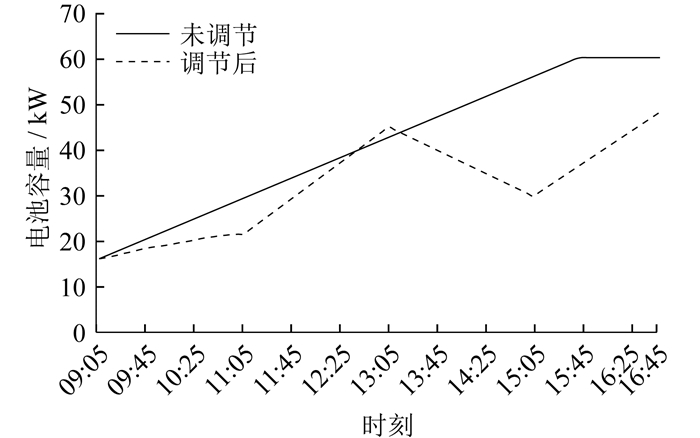
运用电动汽车-充电桩聚合优化调节策略进行MATLAB仿真。电动汽车电池容量变化对比和入网时段内容变化对比如图 3、图 4所示。

由图 3和图 4可知，在可接受调节时间内，由于未接受调节的电动汽车将持续正常充电，从而不仅增加了用户的充电成本，也增大了电网的调节压力。而在保证电动汽车电池容量大于20% 的前提下，通过优化调节策略，可大大减少区域内电动汽车在用电高峰时段(09：00—11：00和13：00—15：00)的充电功率。同时，优化调节策略使得电动汽车在11：00—13：00和15：00—17：00时段利用较低电价尽快充电，在达到用户期望离网电量的同时，保证了电动汽车在用电高峰时段参与需求响应，向电网反向输电降低电网压力。

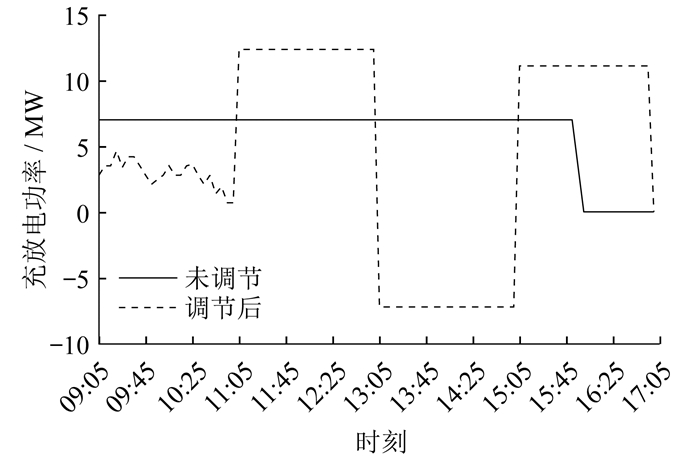
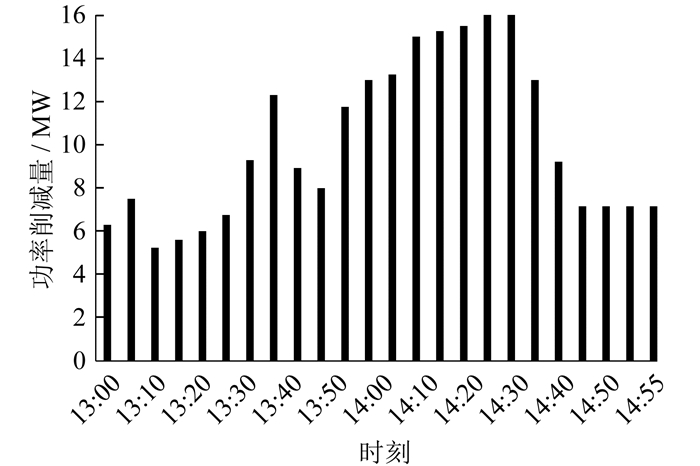
电动汽车-充电桩需求响应时段内功率削减情况如图 5所示。

由实验结果可知，相比于未经调节直接充电，负荷聚合商优化调节参与需求响应使得用户充电费用从93.93元减少至26.36元。这表明电动汽车负荷聚合商通过调节区域内电动汽车-充电桩负荷参与需求响应行为，既降低了电力峰值，又节省了用户支出。

本文以电动汽车-充电桩负荷为切入点，通过分析电动汽车接入状态、充电桩特性等各类约束条件，建立了精细化的单体设备模型和参与需求响应调节模型，提出了优化调度策略和激励补偿措施，从不同层面和角度探讨了需求侧资源参与电网调节的可行性和有效性，为需求侧资源在电力市场中的运用提供了理论和实践支撑，为电力系统的供需平衡和新能源消纳提供了新的思路和方法。