|
|
|
发布时间: 2024-08-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-03-18
中图法分类号: TM721
文献标识码: A
文章编号: 2096-8299(2024)04-0300-09
|
摘要
空调等温控负荷在虚拟电厂(VPP)的优化调度中起着至关重要的作用。针对VPP中新能源功率输出不稳定问题,提出了基于温控负荷参与的多VPP联合调度策略。首先,研究了温控负荷聚合模型,构建了多VPP分布式能源协调互补的联合调度框架,在日前阶段根据预测数据制定联合调度计划,多VPP管理中心对各VPP进行多能互补。其次,在日前阶段引入考虑用户意愿度的温控负荷模型,在日内阶段根据短期预测数据对调度计划进行滚动修正,减少新能源功率输出波动带来的供需偏差。最后,通过MATLAB调用Cplex仿真分析,验证了多VPP联合优化调度策略不仅保证了供电可靠性,还有效减少了预测偏差带来的补偿费用。
关键词
温控负荷; 用户意愿度; 多虚拟电厂; 日前预测; 日内修正
Abstract
Temperature-controlled loads, such as air conditioners, play a crucial role in the optimal scheduling of virtual power plants(VPP). In order to deal with the instability of renewal energy, a joint scheduling strategy of multi-virtual power plant based on the participation of temperature-controlled loads was proposed. Firstly, the temperature-controlled loads'aggregation model is studied, and the multi-virtual power plant's joint dispatching framework of distributed energy resources is constructed. The joint dispatching plan is formulated according to the forecast data in the pre-day stage, the multi-virtual power plant management center carries out multienergy complementarity for each VPP, and the temperature-controlled loads model considering the user's willingness is introduced in the pre-day stage. In the intraday stage, the scheduling plan is revised on a rolling basis according to the short-term forecast data to reduce the supply and demand deviation caused by the instability of renewal energy, and finally the Cplex simulation invoked by Matlab verifies that the proposed strategy not only ensures the reliability of power supply, but also effectively reduces the compensation cost caused by the prediction deviation.
Key words
temperature-controlled load; user's willingness; multi-virtual power plant; preday forecast; short-term forecast revision
伴随双碳目标的提出,如何有效聚合分布式能源、建设新型电力系统成为当下的重要课题[1-2]。作为聚合分布式能源的最有效的方式之一,虚拟电厂(Virtual Power Plant,VPP)包括各类能源、储能设备和负荷,其中,温控负荷在整体负荷中占比大,具有较高可控性,可以积极参与VPP调度优化,减少新能源功率输出不稳定性对电力系统的影响,在保证供电可靠性的同时,提高整体运行的经济性[3-5]。目前,已有不少关于VPP优化调度的研究。从单一时间尺度出发,文献[6]围绕系统运行成本构建了VPP日前调度优化模型。文献[7]结合能源市场价格和系统运行状态,制定了调度策略。文献[8]采用交替方向乘子法,构建了分布式优化调度模型。通过采用多时间阶段的调度模型,文献[9]建立了考虑考核机制的日前实时优化调控模型。文献[10]在VPP优化调度中采用了日前与实时、实时与后续实时的双重耦合。文献[11]构建了面向准线型需求响应的日前、日内两阶段优化策略。上述研究对VPP内部新能源与各柔性负荷间的优化互动进行了研究,但对柔性负荷的具体种类和特性没有详加分析。文献[12]考虑了电热水器的自然开断现象,减小了温控负荷响应误差。文献[13]提出了一种双线性偏微分方程的负荷模型,通过温度参数得到了空调聚合功率。文献[14]在探究温控负荷调度时,考虑了空调用户的意愿度。文献[15]提出了一种温控负荷群联合调控策略,在保证负荷调控精度的同时,提升了温度分布的合理性。文献[16]构建了基于热力学模型的空调负荷模型,讨论其作为虚拟储能设备的作用,但没有考虑用户意愿度这一因素。
针对上述问题,本文提出了基于温控负荷参与的多VPP联合调度策略。首先,构建考虑热舒适度和意愿度的空调负荷聚合功率模型,挖掘温控负荷的响应潜力。然后,引入多VPP协调互补的联合调度框架,采用细化时间尺度、滚动优化的方法,在日前阶段根据预测数据制定调度计划,在日内阶段根据短期预测数据修正调度计划。最后,以包含3类不同VPP的多VPP为例,通过MATLAB编程仿真,分析模型在电能供应与经济运行方面的优势。
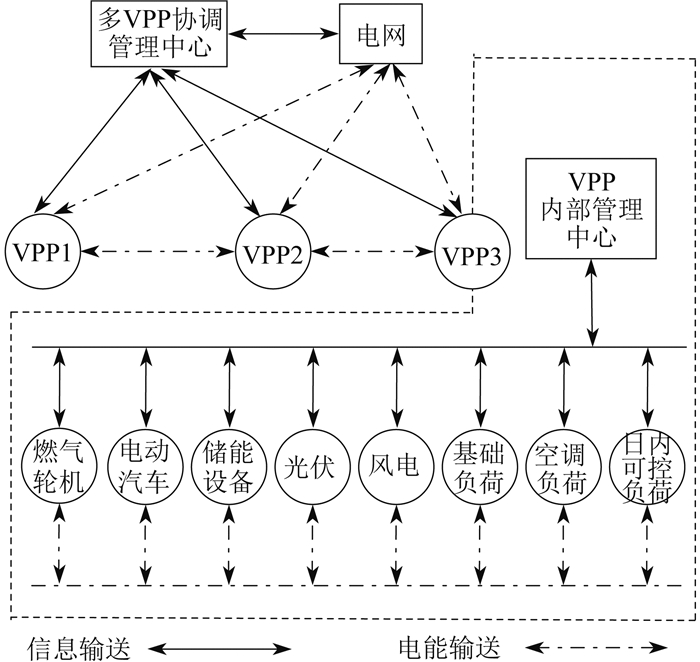
1 多VPP联合调度框架
2 基于用户需求的空调负荷聚合模型
本文采用的空调负荷为具有代表性的温控负荷。空调负荷具有数量庞大、个体差异性大、分散性强等特点,因而对其进行聚合处理,便于整体调度。
2.1 单台空调负荷模型
单台空调的负荷模型可用等效热力学参数模型表示,公式为
| $\left\{\begin{array}{l} \frac{\mathrm{d} T_{\mathrm{m}}(t)}{\mathrm{d} t}=-\frac{1}{C R}\left[T_{\mathrm{m}}(t)-T_{\mathrm{o}}(t)+C_{\mathrm{o}}(t) P_i \delta R\right] \\ C_{\mathrm{o}}(t)= \begin{cases}0, & T_{\mathrm{m}}(t) \leqslant T_{\text {min }} \\ 1, & T_{\mathrm{o}}(t) \geqslant T_{\max } \\ C_{\mathrm{o}}\left(t-d_{\mathrm{e}}\right), & \text { 其他 }\end{cases} \end{array}\right. $ | (1) |
式中:Tm(t),T(ot)——t时刻内、外环境温度;
C,R——内部环境等效热容和热阻;
Co (t)——布尔变量,取0表示空调停运,取1表示运行;
Pi——第i台空调用电功率;
δ——空调能效比;
Tmin,Tmax——空调运行时内部温度的最小值和最大值;
de——极小时滞。
Tmin、Tmax与目标温度Tset的关系可表示为
| $\left\{\begin{array}{l} T_{\min }=T_{\text {set }}-\eta \\ T_{\max }=T_{\text {set }}+\eta \end{array}\right. $ | (2) |
式中:η——空调运行时内部温度允许偏差。
由式(1)可得空调运行时间Ton、停运时间Toff为
| $ \left\{\begin{array}{l} T_{\text {on }}=C R \ln \left(1+x_{\text {on }}\right) \\ x_{\text {on }}=\frac{2 \eta}{P_i \delta R+T_{\text {set }}-\eta-T_{\mathrm{o}}(t)} \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} T_{\text {off }}=C R \ln \left(1+x_{\text {off }}\right) \\ x_{\text {off }}=\frac{2 \eta}{T_0(t)-T_{\text {set }}-\eta} \end{array}\right. $ | (4) |
式中:xon,xoff——中间变量。
单台空调处于运行状态时的概率Kon为
| $K_{\text {on }}=\frac{T_{\text {on }}}{T_{\text {on }}+T_{\text {off }}} $ | (5) |
2.2 多台空调负荷聚合模型
通过统计模拟法,单个VPP中n台空调的聚合功率PN可表示为
| $ \begin{equation*} P_{\mathrm{N}}=\sum\limits_{i=1}^{n} P_{i} K_{\mathrm{on}} \end{equation*} $ | (6) |
将式(6)代入式(5)可得
| $\begin{equation*} K_{\text {on }}=\frac{\ln \left(1+x_{\text {on }}\right)}{\ln \left(1+x_{\text {on }}\right)+\ln \left(1+x_{\text {off }}\right)} \end{equation*} $ | (7) |
由不等式变换可得
| $ \frac{x_{\text {on }} /\left(1+x_{\text {on }}\right)}{x_{\text {on }} /\left(1+x_{\text {on }}\right)+x_{\text {off }} /\left(1+x_{\text {off }}\right)} <K_{\text {on }} <\frac{x_{\text {on }}}{x_{\text {on }}+x_{\text {off }}} $ | (8) |
将式(3)、式(4)代入式(8)可得
| $ \frac{T_{\mathrm{o}}(t)-T_{\mathrm{set}}-\eta}{\delta P_i R} <K_{\mathrm{on}} <\frac{T_{\mathrm{o}}(t)-T_{\text {set }}+\eta}{\delta P_i R} $ | (9) |
在VPP内部,如果空调负荷相关参数各自独立,且都分布于给定的概率密度函数,可近似获得n台空调聚合功率的最大值PNh和最小值PNl,公式为
| $ \left\{\begin{array}{l} P_{\mathrm{N}}^{\mathrm{h}}=\sum\limits_{i=1}^{n} \frac{T_{\mathrm{o}}-T_{\mathrm{set}}-\eta}{\delta R}=n E(Y) \\ E(Y)=E\left(\frac{1}{\delta R}\right)\left[T_{\mathrm{o}}-E\left(T_{\mathrm{set}}\right)-E(\eta)\right] \end{array}\right. $ | (10) |
| $ \left\{\begin{array}{l} P_{\mathrm{N}}^{1}=\sum\limits_{i=1}^{n} \frac{T_{\mathrm{o}}-T_{\mathrm{set}}-\eta}{\delta R}=n E(\boldsymbol{X}) \\ E(X)=E\left(\frac{1}{\delta R}\right)\left[T_{\mathrm{o}}-E\left(T_{\mathrm{set}}\right)+E(\eta)\right] \end{array}\right. $ | (11) |
式中:E(X),E(Y)——随机变量X和Y允许偏差的数学期望;
由此,
| $ \begin{equation*} P_{\mathrm{N}}=\alpha P_{\mathrm{N}}^{\mathrm{h}}+(1-\alpha) P_{\mathrm{N}}^{\mathrm{l}}, \alpha \in[0, 1] \end{equation*} $ | (12) |
2.3 用户需求影响因素
结合ISO 7730—2005《热环境的人体工效学国际标准》的热舒适度标准和预测平均评价热舒适模型可知,空气温度在24.8~27.3 ℃时,人体热舒适度较高。在考虑热舒适度的同时,引入用户意愿度模型。在意愿度模型中,热舒适度与响应潜力的关系受电价影响。当电价高于预期时,响应调度的意愿度升高,反之,则减小。在居民区VPP中,经济收入高的用户对电费的考虑较少,响应调度的意愿度也较低;而年轻和文化程度高的用户对响应调度的兴趣较高。将这些影响因素分别由经济收入因子a1、年龄因子a2、文化程度因子a3代表,可得出用户意愿度模型为
| $ u_{i}^{t}=a\left(\mathrm{e}^{\frac{p_{\mathrm{c}}}{p_{\max }}-1}-\mathrm{e}^{\frac{p_{\mathrm{d}}}{p_{\max }}}-1\right. $ | (13) |
| $ a=\frac{a_{1} a_{2} a_{3}}{\max \left(a_{1}, a_{2}, a_{3}\right)} $ | (14) |
| $ a_{1}= \begin{cases}\mathrm{e}^{-i_{\mathrm{n}}}, & 0 <i_{\mathrm{n}} \leqslant i_{\mathrm{n} 0} \\ \mathrm{e}^{-i_{\mathrm{n} 0}}, & i_{\mathrm{n}} \geqslant i_{\mathrm{n} 0}\end{cases} $ | (15) |
| $ a_2=\varepsilon_0 \mathrm{e}^{-\frac{\left(a_{\mathrm{e}}-a_{00}\right)^2}{2}} $ | (16) |
| $ a_{3}= \begin{cases}\varepsilon_{1}, & 0 <e_{\mathrm{d}} \leqslant e_{\mathrm{d} 1} \\ \varepsilon_{2}, & e_{\mathrm{d} 1} <e_{\mathrm{d}} \leqslant e_{\mathrm{d} 2} \\ \varepsilon_{3}, & e_{\mathrm{d} 2} <e_{\mathrm{d}} \leqslant e_{\mathrm{d} 3}-\frac{\left(a_{\mathrm{c}}-a_{\mathrm{a}}\right)^{2}}{2}\end{cases} $ | (17) |
式中:
a——影响因素的综合因子;
根据上述用户意愿度模型,可得出居民区空调温度可调节范围为
| $ \Delta T_{i}^{t}=u_{i}^{t}\left(T_{\max , 0}^{i, t}-T_{\min , 0}^{i, t}\right) $ | (18) |
| $ T_{\max }^{i, t}=T_{\max , 0}^{i, t}+\Delta T_{i}^{t} $ | (19) |
| $ T_{\min }^{i, t}=T_{\min , 0}^{i, t}-\Delta T_{i}^{t} $ | (20) |
式中:ΔTit——考虑意愿度后空调温度可调节变化量;
商业区与办公区的空调用户意愿度模型与居民区相似。在商业区中,营业收入高的用户响应调度的意愿度低,而店铺租金高的用户乐于参与响应,配备了冰库的特殊类型商店用户响应调度的意愿低。在办公区中,收入高的用户响应调度的意愿度低,而办公室租金高的用户响应调度的意愿度高;国企需要响应国家号召,在节约用电方面有相应目标额度,中小型私企节约用电主要受政策补助的影响。
3 多VPP联合调度的日前-日内优化模型
3.1 日前预测优化模型
3.1.1 日前阶段目标函数
本文研究的多VPP联合调度运行模式分为日前预测优化阶段(以下简称“日前阶段”)和日内滚动修正阶段(以下简称“日内阶段”)。在日前阶段,提前24 h收集每1 h的供需情况,以多VPP整体利益最优为目标,制定调度计划,包括每1 h内各VPP间的电能交互、VPP向电网的购售电、可控能源出力、温控负荷调度等。多VPP整体利益最优目标函数Z的表达式为
| $ \begin{equation*} Z=\max \left[\sum\limits_{i=1}^{n_{\mathrm{p}}} \sum\limits_{t=1}^{T_{\text {ent }}}\left(Z_{i, t}^{\mathrm{nb}}+Z_{i, t}^{\mathrm{dw}}-Z_{i, t}^{\mathrm{aj}}-Z_{i, t}^{\mathrm{cn}}-Z_{i, t}^{\mathrm{qc}}-Z_{i, t}^{\mathrm{bc}}\right)\right] \end{equation*} $ | (21) |
式中:np——VPP数量;
Ttotal——总时间;
Zi,tnb——VPP参与内部调度时的收入;
Zi,tdw——向电网购、售电产生的利润;
| $\begin{equation*} Z_{i, t}^{\mathrm{nb}}=\omega_{t}^{\mathrm{s}} P_{i, t}^{\mathrm{s}}-\omega_{t}^{\mathrm{b}} P_{i, t}^{\mathrm{b}} \end{equation*} $ | (22) |
式中:
| $ \begin{equation*} Z_{i, t}^{\mathrm{dw}}=\omega_{t}^{\mathrm{sw}} P_{i, t}^{\mathrm{sw}}-\omega_{t}^{\mathrm{bw}} P_{i, t}^{\mathrm{bw}} \end{equation*} $ | (23) |
式中:
| $\begin{equation*} Z_{i, t}^{\mathrm{qj}}=d\left(P_{i, t}^{\mathrm{qj}}\right)^{2}+e P_{i, t}^{\mathrm{qj}}+f+\phi_{i, t}^{\mathrm{a}} Z_{\mathrm{a}}^{\mathrm{qj}}+\phi_{i, t}^{\mathrm{b}} Z_{\mathrm{b}}^{\mathrm{qj}} \end{equation*} $ | (24) |
式中:
| $ \begin{equation*} Z_{i, t}^{\mathrm{cn}}=\omega^{\mathrm{cn}}\left(P_{i, t}^{\mathrm{c}}+P_{i, t}^{\mathrm{f}}\right) \end{equation*} $ | (25) |
式中:
| $ \begin{equation*} Z_{i, t}^{\mathrm{qc}}=\sum\limits_{i=1}^{N_{\mathrm{c}}} \frac{Z_{i}^{\mathrm{c}}}{L_{i} S_{i} P_{i}}\left(\frac{P_{i, t}^{\mathrm{qc}}}{\theta^{\mathrm{qc}}}+Q_{i}\right) \end{equation*} $ | (26) |
式中:
| $\begin{equation*} Z_{i, t}^{\mathrm{bc}}=\omega^{\mathrm{bc}} P_{i, t}^{\mathrm{bc}} \phi_{i, t}^{\mathrm{bc}} \end{equation*} $ | (27) |
式中:ωbc——削减负荷单位时间内的补偿费用;
Pi,tbc——削减量;
ϕi,tbc——布尔变量,取0表示不削减负荷,取1表示削减负荷。
3.1.2 日前阶段约束条件
多VPP内部功率约束条件为
| $ \begin{align*} & P_{i, t}^{\mathrm{gff}}+P_{i, t}^{\mathrm{fd}}+P_{i, t}^{\mathrm{bw}}-P_{i, t}^{\mathrm{sw}}+P_{i, t}^{\mathrm{b}}-P_{i, t}^{\mathrm{s}}+P_{i, t}^{\mathrm{qj}}= \\ & P_{i, t}^{\text {load }}+P_{i, t}^{\mathrm{f}}-P_{i, t}^{\mathrm{c}}+P_{i, t}^{\mathrm{qc}} \end{align*} $ | (28) |
式中:
Pi,tload——削减后负荷量。
各VPP间功率约束条件为
| $P_{i, j, t}^{\mathrm{b}}=-P_{i, j, t}^{\mathrm{s}} $ | (29) |
| $ 0 \leqslant P_{i, j, t}^{\mathrm{b}} \leqslant P_{i, j, t}^{\mathrm{bmax}} $ | (30) |
| $ 0 \leqslant P_{i, j, t}^{\mathrm{s}} \leqslant P_{i, j, t}^{\mathrm{smax}} $ | (31) |
式中:
多VPP与电网间功率约束条件为
| $0 \leqslant P_{i, t}^{\text {bw }} \leqslant \phi_{i, t}^{\text {bw }} P_{i, t}^{\text {bw } \max } $ | (32) |
| $ 0 \leqslant P_{i, t}^{\mathrm{sw}} \leqslant \phi_{i, t}^{\mathrm{sw}} P_{i, t}^{\mathrm{sw} \text { max }} $ | (33) |
| $ \phi_{i, t}^{\mathrm{bw}}+\phi_{i, t}^{\mathrm{si}} \leqslant 1 $ | (34) |
式中:Pi,tbw max,Pi,tsw max——向电网购、售电量的最大值;
燃气轮机约束条件为
| $ P_{i, t}^{\mathrm{qimin}} \theta_{i, t}^{\mathrm{qj}} \leqslant P_{i, t}^{\mathrm{qj}} \leqslant P_{i, t}^{\mathrm{qimax}} \theta_{i, t}^{\mathrm{qj}} $ | (35) |
| $-S^{\mathrm{q} \mathrm{min}} \leqslant P_{i, t}^{\mathrm{qj}}-P_{i, t-1}^{\mathrm{qj}} \leqslant S^{\mathrm{q} \max } $ | (36) |
| $ \phi_{i, t}^{\mathrm{y}}+\phi_{i, t}^{\mathrm{t}} \leqslant 1 $ | (37) |
| $ \theta_{i, t}^{\mathrm{qj}}-\theta_{i, t-1}^{\mathrm{qj}} \leqslant \phi_{i, t}^{\mathrm{y}}-\phi_{i, t}^{\mathrm{t}} $ | (38) |
式中:
储能设备约束条件为
| $ 0 \leqslant P_{i, t}^{\mathrm{c}} \leqslant P_{i, t}^{\mathrm{cmax}} $ | (39) |
| $ 0 \leqslant P_{i, t}^{\mathrm{f}} \leqslant P_{i, t}^{\mathrm{fmax}} $ | (40) |
| $ S_{i, t}^{\mathrm{cmmin}} \leqslant S_{i, t}^{\mathrm{cn}} \leqslant S_{i, t}^{\mathrm{cmmax}} $ | (41) |
| $ S_{i, t}^{\mathrm{cn}}=S_{i, t-1}^{\mathrm{cn}}+\theta^{\mathrm{cn} 1} P_{i, t}^{\mathrm{c}}-\frac{P_{i, t}^{\mathrm{f}}}{\theta^{\mathrm{cn} 2}} $ | (42) |
| $ S_{i, 0}^{\mathrm{cn}}=S_{i, t}^{\mathrm{cn}} $ | (43) |
式中:
| $ 0 \leqslant P_{i, t}^{\mathrm{cd}} \leqslant \phi_{i, t}^{\mathrm{cd}} P_{i, t}^{\mathrm{cdmax}} $ | (44) |
| $ 0 \leqslant P_{i, t}^{\mathrm{fd}} \leqslant \phi_{i, t}^{\mathrm{fd}} P_{i, t}^{\mathrm{dd} m a x} $ | (45) |
| $S_{i, t}^{\mathrm{qc}}=S_{i, t-1}^{\mathrm{qc}}+\theta^{\mathrm{qf}} P_{i, t}^{\mathrm{cd}}-\frac{P_{i, t}^{\mathrm{fd}}}{\theta^{\mathrm{qc}}} $ | (46) |
| $ S_{i, t}^{\mathrm{qcmin}} \leqslant S_{i, t}^{\mathrm{qc}} \leqslant S_{i, t}^{\mathrm{qcmax}} $ | (47) |
式中:
3.2 日内滚动修正模型
3.2.1 日内阶段目标函数
在日内阶段,提前4 h,以15 min为1个时间段,分段收集光伏、风电输出功率和负荷需求,以功率偏差惩罚和修正成本最低为目标,对日前计划进行修正。目标函数
| $ \begin{align*} & M=\min \sum\limits_{t=t_{0}}^{T_{\mathrm{n}}}\left(\omega_{t}^{\mathrm{bw}} \eta^{\mathrm{bw}} P_{i, t}^{\mathrm{bp}}-\omega_{t}^{\mathrm{sw}} \eta^{\mathrm{sw}} P_{i, t}^{\mathrm{sp}}+Z_{i, t}^{\mathrm{qjrn}}+\right. \\ & \left.\quad Z_{i, t}^{\mathrm{cnrn}}+Z_{i, t}^{\mathrm{qcrn}}+Z_{i, t}^{\mathrm{rn}}\right) \end{align*} $ | (48) |
式中:
3.2.2 日内阶段约束条件
多VPP内部功率约束条件为
| $ \begin{align*} & P_{i, t}^{\mathrm{gf} 2}+P_{i, t}^{\mathrm{fd} 2}+P_{i, t}^{\mathrm{bp}}+P_{i, t}^{\mathrm{bw}}-P_{i, t}^{\mathrm{sp}}-P_{i, t}^{\mathrm{sw}}+P_{i, j}^{\mathrm{b}} \\ & -P_{i, j, t}^{\mathrm{s}}+P_{i, t}^{\mathrm{qj}}=P_{i, t}^{\text {load} 2}+P_{i, t}^{\mathrm{c}}-P_{i, t}^{\mathrm{f}}+P_{i, t}^{\mathrm{qc}} \end{align*} $ | (49) |
式中:
日内阶段可控负荷约束条件为
| $ 0 \leqslant P_{i, t}^{\mathrm{rn}} \leqslant P_{i, t}^{\mathrm{rnmax}} $ | (50) |
| $ \left|P_{i, t}^{\mathrm{rn}}-P_{i, t-1}^{\mathrm{rn}}\right| \leqslant P_{c}^{\mathrm{rn}} $ | (51) |
| $ \sum\limits_{t=1}^{T} \phi_{i, t}^{\mathrm{rn}} \leqslant K $ | (52) |
| $ \sum\limits_{t = 1}^{t + t_s^{\max } + 1} {\left( {1 - \phi _{i,t}^{{\rm{ma}}}} \right)} \ge 1 $ | (53) |
| $\sum\limits_{t = 1}^{t + t_s^{\max } - 1} {\phi}_{i, t}^{\mathrm{rn}} \geqslant t_{s}^{\min }\left(\phi_{i, t}^{\mathrm{mn}}-{\phi}_{i, t-1}^{\mathrm{m}}\right) $ | (54) |
式中:
4 算例分析
4.1 基础数据
本文模型在MATLAB中调用Cplex算法进行求解。其中,多VPP联合调度3个不同类型的VPP,包括居民区、商业区和办公区。电网电价参考上海电网2023年4月发布的电价。
各VPP燃气轮机参数如表 1所示。各VPP中储能设备参数如表 2所示。
表 1
各VPP燃气轮机参数
| VPP | 爬坡速率/(kW/h) | 输出功率/kW | 启停费用/元 |
| 居民区 | 800 | 800~3 000 | 300/150 |
| 商业区 | 500 | 500~1 500 | 210/100 |
| 办公区 | 400 | 400~2 000 | 180/100 |
表 2
各VPP储能设备参数
| VPP | 设备容量/kWh | 充放电速度/(kW/h) | 起始容量/kWh |
| 居民区 | 7 000 | 1 200 | 3 000 |
| 商业区 | 8 500 | 1 200 | 4 000 |
| 办公区 | 7 000 | 1 000 | 3 500 |
各VPP中均有500辆电动汽车,其参数如表 3所示。
表 3
各VPP电动汽车参数
| VPP | 始末电量/kWh | 出行时间/h | 行驶路程/km |
| 居民区 | 9.0/10.5 | 7/11/13/18 | 8/8/8/8 |
| 商业区 | 31.0/40.2 | 8/19 | 17/17 |
| 办公区 | 15.0/26.4 | 8/17 | 15/15 |
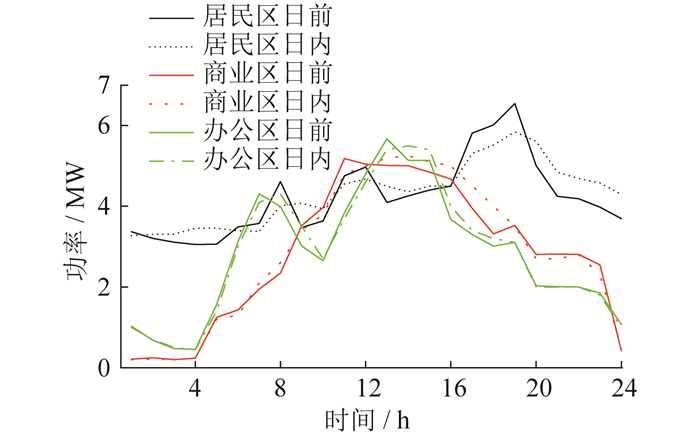
各VPP中空调负荷参数及取值如表 4所示。各VPP日前、日内阶段预测负荷如图 2所示。
表 4
各VPP单台空调负荷参数
| 参数 | 取值范围 |
| 等效热阻/(K/kW) | [5.12, 7.25] |
| 等效热容/(kWh/K) | [0.17, 0.21] |
| 用电功率/kW | [2.4, 3.5] |
| 允许温度偏差/K | [0, 1] |
| 能效比 | [3.1, 3.2] |
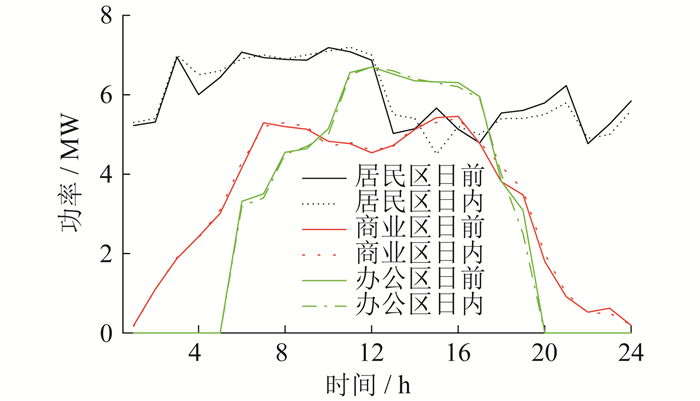
各VPP中光伏、风电等新能源在日前、日内阶段的预测输出功率如图 3所示。
4.2 空调负荷响应潜力结果
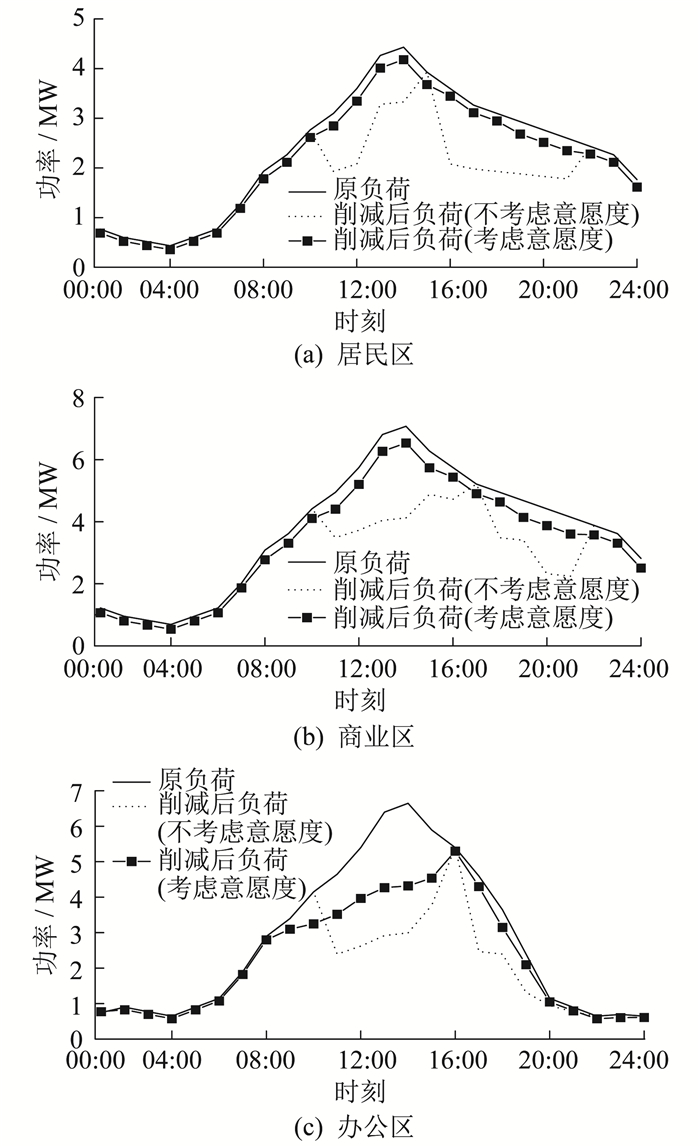
4.2.1 空调负荷响应潜力结果分析
4.2.2 空调负荷对联合调度的影响
考虑用户热舒适度、意愿度等因素,采用聚合功率模型获取空调作为温控负荷的弹性响应潜力特性,可以提高联合调度的经济性。在不考虑温控负荷特性、将空调作为基础负荷时,以居民区为例,观察日前阶段的调度结果。空调作为基础负荷时居民区日前调度结果如图 5所示。
由图 5可知,在将空调作为基础负荷时,空调负荷不会进行削减,在每日06:00—09:00、13:00— 21:00时段的用电高峰时期,居民区VPP需大量向外部电网购电。空调作为基础负荷和温控负荷两种情况下的各VPP收益如表 5所示。
表 5
两种情况下各VPP收益
| 情况 | 居民区收益 | 商业区收益 | 办公区收益 |
| 空调负荷作为基础负荷 | 24 645 | 18 876 | 28 387 |
| 空调负荷作为温控负荷 | 29 652 | 25 176 | 34 927 |
由表 5可以看出,空调负荷作为基础负荷时,各VPP的购电需求逐渐增大,而购电时段恰逢电价高峰,对VPP的经济运行造成了负面影响,使得运行成本增加,收益下降。
4.3 日前预测优化结果
4.3.1 日前阶段调度结果分析
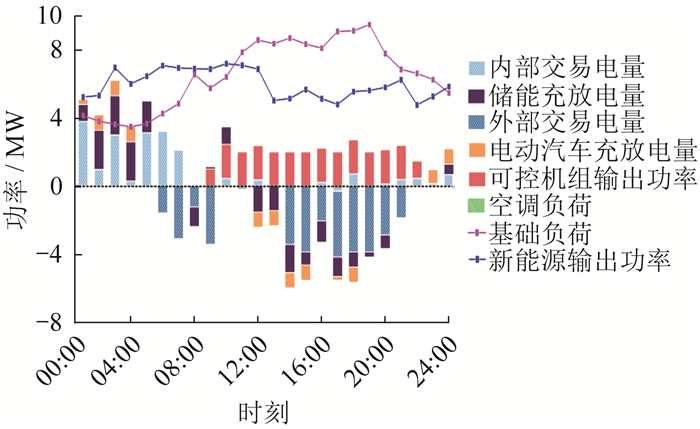
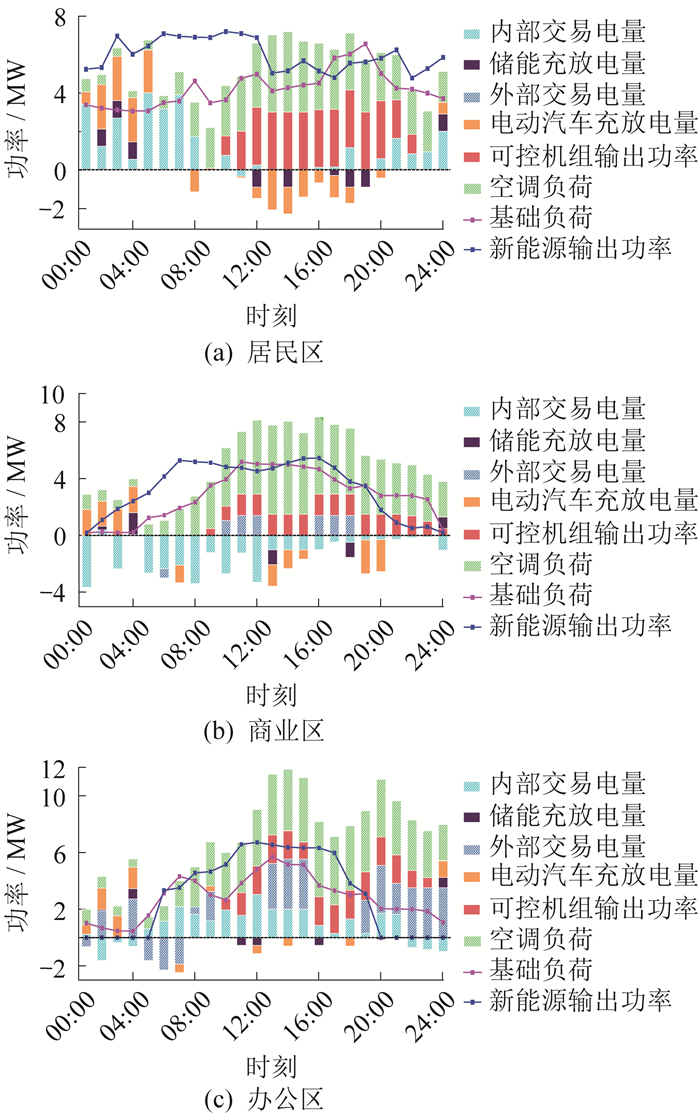
各VPP日前阶段调度结果如图 6所示。
由图 6可知,在日前阶段,各VPP中储能设备的充放电趋势相似,受电价影响较大,每日23:00到次日07:00时段电价较低,储能设备大多处于充电状态,而白天电价高时大多处于放电状态,从而提高了VPP运行的经济性。电动汽车同时受到电价和出行模式的影响,在每日23:00至次日05:00时段电价低时充电,白天车辆行驶时放电。各VPP的燃气轮机在每日09:00开始参与调度,其中居民区的燃气轮机输出功率高,启停成本较低,且爬坡速率大,可以及时对新能源输出功率波动做出反应,保证稳定供电。各VPP除了积极调用自身资源外,还可以进行电能交互,或向电网进行购售电。在居民区,由于每日00:00—9:00时段,风电输出功率充足,VPP供自身负荷充电后,尚有大量剩余电能,因此可以优惠价格传输给其他两个VPP;到了白天,除了光伏、风电输出功率,居民区配备的高功率、高爬坡速率燃气轮机也保证了供电的可靠性,使得VPP在满足自身需求同时,积极与其他VPP互动。在商业区,每日05:00—16:00时段,由于负荷用电量大,因此商业区主要从其他两个VPP购电,极少向电网进行购电。此外,商业区的燃气轮机启停成本高,而向其他VPP购电减少了自身燃气轮机的启停,从而降低了运营成本。在办公区,由于燃气轮机输出功率受限,且新能源以光伏为主,为满足用电需要,VPP会向其他VPP购电;随着08:00后用户逐渐增多,VPP只能向电网购买高价电能;18:00后,由于光伏不再输出功率,VPP需持续向电网购电。
4.3.2 多VPP联合调度经济性分析
单独调度和联合调度两种调度方案下各VPP收益如表 6所示。
表 6
两种调度方案下各VPP收益
| 方案 | 居民区收益 | 商业区收益 | 办公区收益 |
| 单独调度 | 18 543 | 15 996 | 25 682 |
| 联合调度 | 29 652 | 25 176 | 34 927 |
单独调度和联合调度两种调度方案下各VPP向外网购电情况如表 7所示。
表 7
两种调度方案下各VPP向外网购电情况
| 方案 | 居民区购电量/kW | 商业区收益/元 | 办公区收益/元 |
| 单独调度 | −13 502.8 | 12 303.9 | 15 293.7 |
| 联合调度 | −2 265.7 | 7 491.4 | 9 427.9 |
由表 6、表 7可知,居民区电能充足,在满足自身供给情况下还可以向外部售电,而商业区、办公区则需要向外部购电。在单独调度时,商业区、办公区所亏欠的电能需全部向电网购买。进行联合调度时,则可以向居民区购电,减少向电网的购电量。由于内部电价低于外部电价,从而不仅实现整体利益的最大化,还提高了各VPP的单独收益。
4.4 日内滚动修正结果
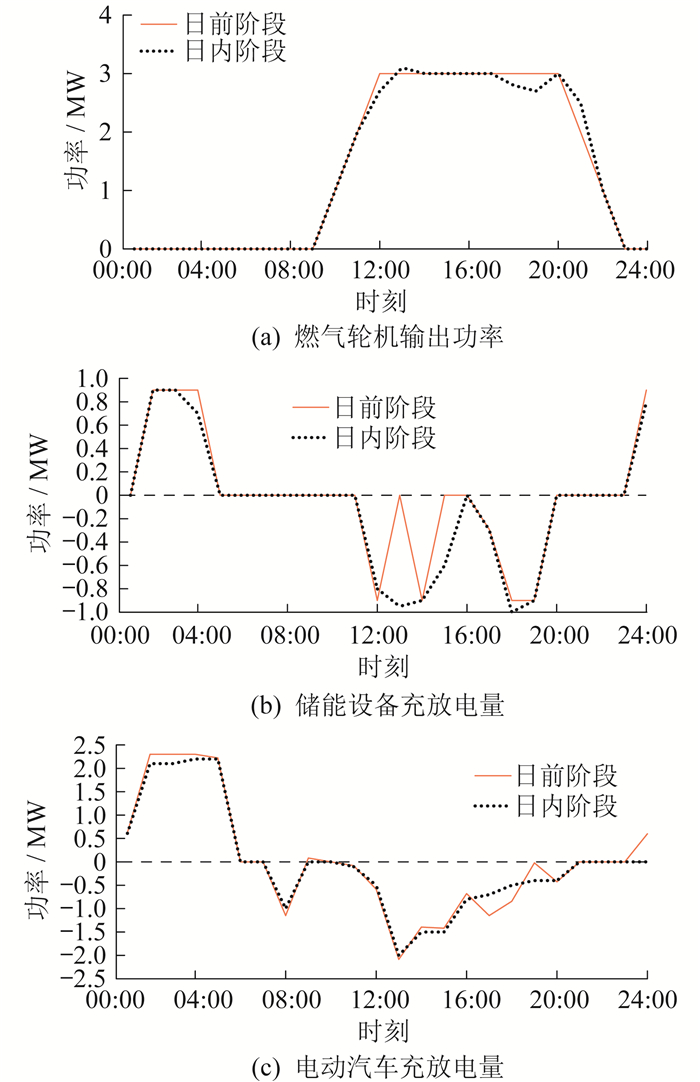
4.4.1 日前、日内阶段优化结果对比
4.4.2 日内阶段策略对比
本文的日内阶段策略主要是通过调整各类分布式能源功率,对日前阶段调度计划进行修正。如果不修正日前阶段中各能源功率,则日内阶段出现的不平衡功率全部交由外部电网消纳。两种方案下日内阶段各VPP成本如表 8所示。
表 8
两种方案下日内阶段各VPP成本
| 方案 | 居民区成本 | 商业区成本 | 办公区成本 |
| 不修正 | 4 376 | 3 562 | 4 747 |
| 修正 | 2 132 | 1 838 | 2 573 |
由表 8可知,在对分布式能源进行修正时,日内阶段成本主要来自于功率惩罚偏差和调整费用;若不修正,日内阶段成本来自于功率惩罚偏差和向电网购电成本,高于修正时成本。总之,通过修正日前调度计划消纳主要偏差功率,可以节约运营成本、增加整体收益。
5 结论
本文构建了多VPP联合调度优化模型,包括日前预测优化和日内滚动修正两个阶段,并在日前阶段引入考虑用户意愿度的空调负荷,得到以下结论。
(1) 在构建空调聚合功率模型时,综合考虑用户热舒适度、意愿度等因素,使得预测的空调负荷响应潜力更加符合实际情况,提高了调度计划的准确性和经济性。
(2) 多VPP协调管理中心对各VPP进行综合管理,收集各VPP的电能供需情况,结合电网电价,制定调度计划,各VPP根据计划进行电能交互,提高了多VPP运行的经济性。
(3) 在日前阶段,根据预测数据制定联合调度计划,多VPP协调管理中心对各VPP进行能源互补;在日内阶段,根据短期预测数据对调度计划进行滚动修正,减少了新能源功率输出波动带来的供需偏差,不仅保证了供电的可靠性,还有效减少了预测偏差带来的补偿费用。
参考文献
-
[1]魏震波, 孙舟倍, 梁政. 基于多目标两阶段规划的虚拟电厂优化调度[J]. 南方电网技术, 2023, 17(4): 109-118.
-
[2]黄蔚亮, 苏志鹏, 梁欣怡, 等. 考虑可调市场和外部需求响应的虚拟电厂优化运行策略[J]. 中国电力, 2023, 56(12): 156-163.
-
[3]王健, 郑峻峰, 黄际元, 等. 虚拟电厂关键技术综述与发展展望[J]. 供用电, 2023, 40(12): 43-54.
-
[4]张涛, 李逸鸿, 郭玥彤, 等. 考虑虚拟电厂调度方式的售电公司多时间尺度滚动优化[J]. 电力系统保护与控制, 2021, 49(11): 79-87.
-
[5]潘凯岩, 胡林麟, 吴俊越, 等. 面向综合能源协调的虚拟电厂调控平台设计与规划优化[J]. 可再生能源, 2024, 42(1): 127-135.
-
[6]赵书豪, 王进, 张孝跃. 考虑综合需求响应的虚拟电厂日前调度优化策略[J]. 现代电力, 2023, 40(6): 976-984.
-
[7]张宁, 朱昊, 杨凌霄, 等. 考虑可再生能源消纳的多能互补虚拟电厂优化调度策略[J]. 发电技术, 2023, 44(5): 625-633.
-
[8]SHAFIEKHANI M, AHMADI A, HOMAEE O, et al. Optimal bidding strategy of a renewable-based virtual power plant including wind and solar units and dispatchable loads[J]. Energy, 2022, 239: 122379.
-
[9]杨康, 杨苹, 曾宪锴, 等. 电力现货市场环境下虚拟电厂的优化调控策略[J]. 电气自动化, 2023, 45(5): 11-15.
-
[10]赵冬梅, 郭育村, 郑亚锐. 考虑需求响应的虚拟电厂两阶段市场竞标模型[J]. 现代电力, 2023, 40(2): 182-191.
-
[11]成雨阳, 高红均, 王仁浚, 等. 虚拟电厂两阶段准线型需求响应优化及收益共享-风险共担决策方法[J]. 电网技术, 2024, 48(2): 799-809.
-
[12]孙毅, 王欣, 许鹏, 等. 基于预切换状态的电热水器负荷群调控策略[J]. 现代电力, 2019, 36(5): 68-75.
-
[13]BASHASH S, FATHY H K. Modeling and control of aggregate air conditioning loads for robust renewable power management[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1318-1327.
-
[14]LU N. An evaluation of the HVAC load potential for pro-viding load balancing service[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1263-1270.
-
[15]许鹏, 孙毅, 谢祥颖, 等. 异构温控负荷群模型优化及联合调控策略[J]. 电力科学与技术学报, 2021, 36(5): 120-128.
-
[16]王怡岚, 童亦斌, 黄梅, 等. 基于需求侧响应的空调负荷虚拟储能模型研究[J]. 电网技术, 2017, 41(2): 394-401.