|
|
|
发布时间: 2024-08-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-02-01
基金项目: 国家自然科学基金(51977127);上海市教育发展基金会和上海市教育委员会“曙光计划”(20SG52)
中图法分类号: TM9
文献标识码: A
文章编号: 2096-8299(2024)04-0293-07
|
摘要
为了解决现行各类基线负荷预测方法对时序性的依赖及多影响因素分类分析评估不准确等问题,提出了一种基于改进条件生成对抗网络(CGAN)和图卷积神经网络(GCN)的需求响应潜力预测方法。首先,引入融合CGAN和Wasserstein生成对抗网络(WGAN)的Wasserstein条件生成对抗网络(WCGAN),并利用历史数据训练生成器和判别器,估计基线负荷;然后,充分考虑基线与响应负荷的不确定性,提出了一种基于WCGAN和GCN的需求响应负荷预测方法;最后,采用实际负荷数据对所提方法的有效性进行了分析。
关键词
需求响应; 基线负荷; 响应潜力; Wasserstein条件生成对抗网络; 图卷积神经网络
Abstract
In order to solve the problems such as the dependence of the existing various baseline load estimation methods on temporality and the inaccurate assessment of the classification analysis of multiple influencing factors, a user-side flexibility resource response potential assessment method based on the improved conditional generative adversarial networks(CGAN)and graph convolutional neural networks(GCN)is proposed. Firstly, a fusion of wasserstein generative adversarial networks (WGAN) and CGAN is introduced to create. Wasserstein conditional generative adversarial networks(WCGAN), and historical data are used to train the generator and discriminator to estimate the baseline load; then, with full consideration of the uncertainty of the baseline and response loads, we propose an approach based on the WCGAN and GCN; finally, the effectiveness of the proposed method is analysed by using actual load data.
Key words
demand response; baseline load; response potential; Wasserstein conditional generative adversarial network; graph convolutional neural network
用户侧灵活性资源的响应潜力预测在电力系是评估用户侧灵活性资源响应能力的基础,通过准统的需求侧管理中占有重要地位[1]。基线负荷估计确估计基线负荷,能够确定用户改变用电行为(减少或增加用电量)时,实际节省或增加了多少电量。这对规划电力系统的运行、优化能源分配、提高能效以及促进可再生能源整合等方面至关重要[2]。
目前,关于基线负荷估计的研究方法主要包括平均法、聚类法、回归法,以及神经网络算法4种。平均法,通常采用事件日之前10 d或5 d的典型日负荷数据,通过计算其平均值来估算事件日的基线负荷,但该方法准确度较低。聚类法,是一种无监督学习方法,在基线负荷估计研究中主要采用K-means算法,但该算法要假设所有变量具有相同的方差,这在现实中较难成立[3-8]。回归法,是基于大量观测数据、通过数理统计方法建立因变量与自变量间的回归关系表达式,但其对数据连续性要求较高,数据断层将严重影响结果的准确性[9-12]。神经网络算法,其准确度高,并行分布处理能力、鲁棒性以及容错能力强,能够紧密逼近复杂的非线性关系,并具备联想记忆功能[13]。
目前,对于需求响应能力的评估主要源自两种思路。一是根据用户用电特性评估用户在不同环境下能实现的需求响应效果,但这种思路仅考虑用户未响应时的负荷,并根据未响应时的特征预测响应潜力,未考虑响应本身对用户负荷的影响[14-16];二是计算响应负荷与基线负荷的差值,但这种思路很少考虑到基线负荷的不确定性[17-19]。
为了解决以上问题,本文提出了一种用户侧灵活性资源的响应能力预测方法。通过引入Wasserstein条件生成对抗网络(Wasserstein Condition Generative Adversarial Networks,WCGAN),结合条件生成对抗网络(Conditional Generative Adversarial Nets,CGAN)和Wasserstein生成对抗网络(Wasserstein Generative Adversarial Networks,WGAN)的特点,利用历史数据训练生成器和判别器,得到了基于WCGAN基线负荷估计方法。此外,基于WCGAN和图卷积神经网络(Graph Convolutional Network,GCN)提出了需求响应负荷预测方法,通过实际负荷数据验证了所提方法的有效性。
1 基于WCGAN的基线负荷估计模型
1.1 CGAN与WGAN
CGAN是在卷积生成网络的基础上引入了条件变量,这些条件变量可以是类标签、部分数据信息或任何形式的辅助信息。将条件变量同时输入到生成模型和判别模型中,则生成的数据与条件变量相关联。这使得CGAN能够按照指定的条件生成数据,大大增强了模型的应用范围和灵活性。本文通过简化输入数据构建CGAN模型,在算法框架内映射出基线负荷与相关影响因素间的复杂关联性[20]。
WGAN采用Wasserstein距离作为损失函数,进而优化训练过程。Wasserstein距离提供了一种更合理的方式来衡量分布之间的距离[21]。
CGAN能够接受非时序性数据以及根据影响因素筛选数据集,WGAN可以避免梯度消失和模式崩溃,本文结合两者的特点,构建了计算能力强且能够适应大数据量、多影响因素的数据集的WCGAN模型。
1.2 基于WCGAN的基线负荷估计方法
WCGAN的结构与CGAN类似。将噪声值与条件值作为生成器的输入值,由生成器生成预测值,将其与真实值进行比较;两者之间的差异程度由Wasserstein距离表示,并反馈给生成器和判别器;最后得出最接近真实数据的输出值。
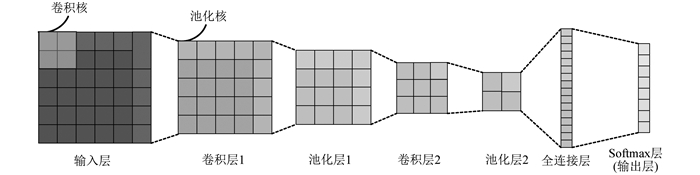
本文选择卷积神经网络作为生成器和判别器的结构,具体如图 1所示。
卷积神经网络由2个卷积层、2个池化层和1个全连接层组成。输入生成器的矩阵由条件值和噪声值拼接形成。
WCGAN的综合损失函数为
| $ \begin{gathered} \min _Z \max _B V(D, G)=E_{X-P_X}\{\log [D(X)]\}+ \\ E_{X^{\prime} \sim P_X}\left\{\log \left[1-D\left(X^{\prime}\right)\right]\right\} \end{gathered} $ | (1) |
式中:Z——生成器;
B——判别器;
V(×)——损失系数;
D(×)——判别器输出的数据;
G——生成器输出的数据;
E(×)——对应分布的期望值;
X~PX——真实值X的分布;
X′~PX′——预测值X ′的分布。
理想状态下生成器的损失函数无限趋近于零,即minZ=0。
本文的目标函数为
| $ \min _Z \max _{\left\|B_{\rm{L}}\right\| \leqslant 1} V(D, G)=E_{X-P_x}\left[D(X)-E_{X^{\prime} \sim P_x} D\left(X^{\prime}\right)\right] $ | (2) |
| $ \left|f\left(x_1\right)-f\left(x_2\right)\right| \leqslant K\left(x_1-x_2\right) $ | (3) |
式中:BL——加了Lipschitz连续的判别器;
f——存在实数集子集的函数;
x1,x2——实数集子集中的任意元素;K——常数。
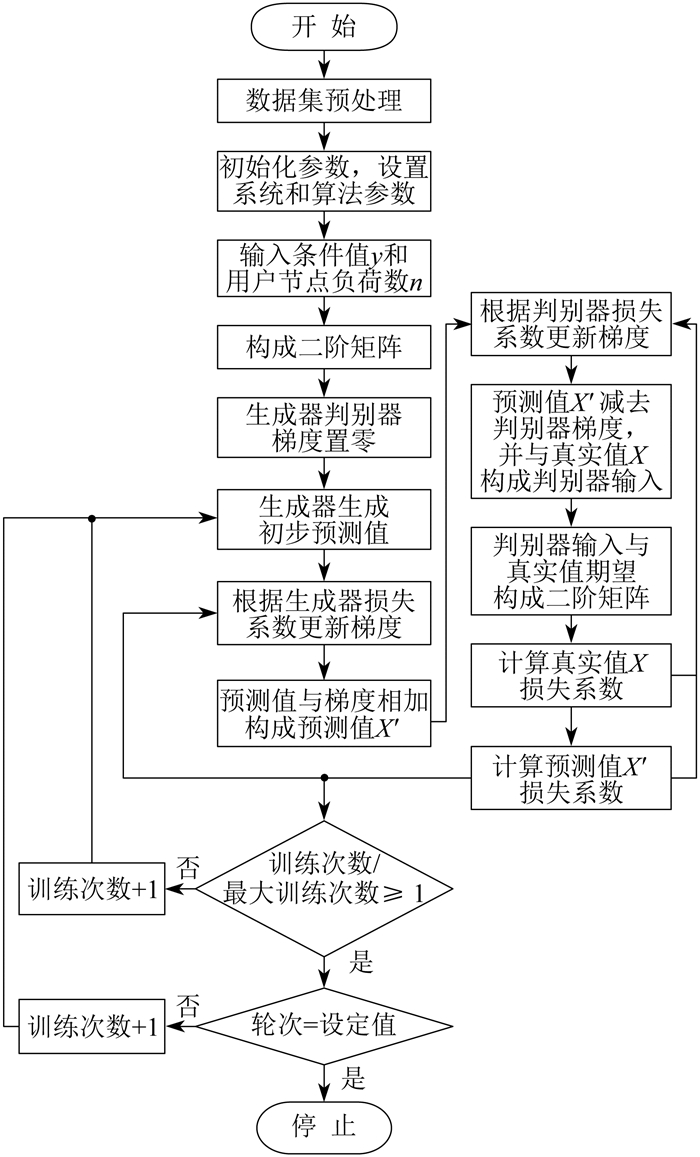
WCGAN的计算步骤如下。
步骤1 数据集预处理。获取目标用户的负荷曲线历史数据,作为训练样本集与验证样本集。对试验数据采用归一化操作,公式为
| $ x_t=\frac{x-x_{\min }}{x_{\max }-x_{\min }} $ | (4) |
式中:xt——归一化输出数据;
x——输入数据;
xmin——原始数据的最小值;
xmax——原始数据的最大值。
步骤2 系统参数设置。设置本次计算的轮次、最大训练次数和条件值y。
步骤3 基于生成模型建立预测模型。采用标准化数据xt作为输入值,生成一个由用户负荷节点数量决定维度的样本矩阵,并通过深度特征提取,对上述矩阵中的负荷值特征进行深入分析。
步骤4 基于判别模型进行深度特征提取。将生成器输出的预测值与真实值期望结合成的矩阵(n × n)作为输入1,将数据集中的真实值与真实值期望结合成的矩阵(n × n)作为输入2。计算每个用户负荷节点对应的预测值、真实值与真实值期望的Wasserstein距离,并构成新的矩阵。通过深度特征提取,对上述矩阵中的负荷值特征进行深入分析。
步骤5 WCGAN模型的优化训练。生成器和判别器收到损失系数后分别更新梯度。由生成器生成的预测值经过生成器和判别器梯度的调整后,与真实值期望构成矩阵。
步骤6 基线负荷预测。将历史负荷数据和条件值输入已经过优化训练的WCGAN后,生成器输出负荷预测值。
2 基于GCN的响应负荷预测模型
2.1 GCN的计算原理
GCN的核心是图卷积操作[23],主要通过以下步骤实现。
步骤1 邻域聚合。对于图中的每个节点,GCN通过聚合其邻居节点的特征信息来更新该节点的特征表示。
步骤2 特征变换。聚合邻域信息后,GCN通常会对结果进行线性变换(如乘以权重矩阵),并应用非线性激活函数,以增强模型的表达能力。
步骤3 层叠结构。通过层叠多个图卷积层,GCN能够捕捉节点间的更高阶关系,逐层提取更抽象的图特征。
GCN每一层的计算公式为
| $ \boldsymbol{s}\left(H^{(l)}, \boldsymbol{A}\right)=\sigma\left(\boldsymbol{U}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{U}^{-\frac{1}{2}} H^{(l)} \boldsymbol{W}^{(l)}\right) $ | (5) |
式中:s——该层的输出值;
H(l)——l层的特征,对于输入层,H为输入值S;
A——节点数据;
σ——非线性激活函数;
U——A的度矩阵;
W(l)——l层的权重矩阵。
在GCN中,输入一个图,通过l层GCN后,每个节点的特征从输入值S变成了输出值C,用Y表示节点的标签。本文的输入值S为噪声数据,训练集每一层都代表了不同影响因素对于曲线的影响,包括温度、天气、日期类型等,输出值C表示对负荷的效果,Y为最终的负荷曲线。无论中间有多少层,节点数据A都是共享的。
2.2 基于GCN的响应负荷预测方法
基于GCN的响应负荷预测主要包括以下4个步骤。
步骤1 数据集预处理。与前文相同,为了消除不同数据量纲的影响,需要对数据进行归一化操作。
步骤2 GCN计算。给定图R =(S,F),GCN的输入值是一个维度为yt × F的特征矩阵,其中yt为该图的条件值,F为网络中的节点值。通过深度特征提取,对上述矩阵中的负荷值特征进行深入分析。其中,GCN运算时需要输入的数据包括图数据、计算次数和图条件值yt。
步骤3 GCN模型的反向传播优化。通过比较实际输出值与训练数据标签之间的误差来判断模型的准确性,并通过调整核参数的方式降低误差,调整公式为
| $ X_{\mathrm{er}}^{\prime}=X_{\mathrm{er}}+B_{\mathrm{p}}\left(\alpha E_0\right) $ | (6) |
式中:Xer,Xer'——调整前、后的核参数;
Bp (·)——反向传播的运算函数;
α——学习率,用于改变核参数的调整幅度;
E0——实际输出值与数据标签之间的误差,通常为二者的方差。
步骤4 负荷预测。将历史负荷数据和条件值输入已经过优化训练的GCN后,输出负荷预测值。
3 算例分析
3.1 数据来源
本文选取上海某新能源汽车充电服务企业在2022年1月1日至2022年12月31日期间的实际负荷数据及相关影响因素作为研究对象,采用96点法对某一日中的电力负荷进行细致划分,将该日划分为96个时段,每15 min记录一次数据。将影响负荷曲线的因素分为日期类型、温度、天气、风向、风速以及与日期临近程度6种。选取该用户2022年中发生响应事件的8月15日和8月18日进行响应能力预测,申报响应容量分别为200 kW和100 kW。
3.2 基于WCGAN的响应后基线负荷估计算例
为了验证基于WCGAN的基线负荷估计方法的有效性,选择同样对多影响因素和非线性数据集具有分析能力的GCN算法作为对比。
3.2.1 模型准确性评价指标
均方根误差RMSE公式为
| $ R_{\mathrm{MSE}}=\sqrt{\frac{\sum\limits_{i=1}^m\left(x_i^{\prime}-x_i\right)^2}{m}} $ | (7) |
式中:i——样本编号;
m——样本数量;
x'i——预测负荷值;
xi——实际负荷值。
平均绝对百分误差MAPE公式为
| $ M_{\mathrm{APE}}=\frac{1}{m} \sum\limits_{i=1}^m \frac{\left|x_i^{\prime}-x_i\right|}{x_i} \times 100 \% $ | (8) |
平均百分比误差MPB公式为
| $ M_{\mathrm{PB}}=\frac{1}{m} \sum\limits_{i=1}^m \frac{x_i^{\prime}-x_i}{x_i} \times 100 \% $ | (9) |
平均绝对误差MAE公式为
| $ M_{\mathrm{AE}}=\frac{1}{m} \sum\limits_{i=1}^m\left|x_i^{\prime}-x_i\right| $ | (10) |
平均相对百分比误差MRPE公式为
| $ M_{\mathrm{RPE}}=\frac{1}{m} \sum\limits_{i=1}^m \frac{\left|x_i^{\prime}-x_i\right|}{x_i^{\prime}} \times 100 \% $ | (11) |
3.2.2 算例结果与分析
综合考虑6种关键因素,选定与8月15日条件高度相似的8月19日作为基线负荷的理论真实值参考日。
使用2022年一整年数据作为数据集,WCGAN、GCN和国家标准平均法(以下简称“平均法”)3种方法的预测结果和误差(取绝对值)如表 1所示。评价指标结果如表 2所示。
表 1
整年数据集下3种方法的预测结果及误差
| 时刻 | 真实值 | WCGAN | GCN | 平均法 | |||||
| 预测结果 | 误差 | 预测结果 | 误差 | 预测结果 | 误差 | ||||
| 12:15 | 565.2 | 555.0 | 10.2 | 517.1 | 48.1 | 541.4 | 23.8 | ||
| 12:30 | 502.0 | 451.0 | 51.0 | 587.8 | 85.8 | 549.3 | 47.3 | ||
| 12:45 | 454.0 | 446.7 | 7.3 | 406.8 | 47.2 | 579.2 | 125.2 | ||
| 13:00 | 483.2 | 466.6 | 16.6 | 445.0 | 38.2 | 571.9 | 88.7 | ||
| 13:15 | 470.0 | 474.7 | 4.7 | 435.5 | 34.5 | 524.8 | 54.8 | ||
| 13:30 | 401.6 | 467.3 | 65.7 | 336.0 | 65.6 | 490.6 | 89.0 | ||
| 13:45 | 355.2 | 370.0 | 14.8 | 331.3 | 23.9 | 441.4 | 86.2 | ||
| 14:00 | 302.0 | 326.4 | 24.4 | 310.0 | 8.0 | 407.5 | 105.5 | ||
| 14:15 | 276.8 | 252.9 | 23.9 | 215.1 | 61.7 | 353.8 | 77.0 | ||
| 14:30 | 294.0 | 291.0 | 3.0 | 268.0 | 26.0 | 400.5 | 106.5 | ||
| 14:45 | 317.6 | 344.3 | 26.7 | 325.9 | 8.3 | 376.7 | 59.1 | ||
| 15:00 | 359.2 | 363.8 | 4.6 | 344.3 | 14.9 | 436.8 | 77.6 | ||
| 15:15 | 554.8 | 544.1 | 10.7 | 529.2 | 25.6 | 559.9 | 5.1 | ||
| 15:30 | 653.2 | 626.8 | 26.4 | 669.2 | 16.0 | 620.4 | 32.8 | ||
| 15:45 | 769.2 | 760.0 | 9.2 | 679.6 | 89.6 | 617.2 | 152.0 | ||
| 16:00 | 756.8 | 759.7 | 2.9 | 673.0 | 83.8 | 620.8 | 136.0 | ||
表 2
整年数据集下3种方法的评价指标结果
| 方法 | RMSE/kW | MAPE/% | MPB/% | MAE/kW | MRPE/% |
| WCGAN | 25.50 | 4.59 | 0.37 | 18.88 | 4.51 |
| GCN | 50.14 | 12.05 | −5.94 | 42.33 | 9.30 |
| 平均法 | 88.31 | 25.05 | 12.92 | 79.19 | 16.17 |
由表 1可以看出,WCGAN估测的基线负荷与理论真实值的吻合度最高,其准确度显著优于GCN和平均法。由表 2数据可知,WCGAN的RMSE相较于GCN和平均法分别下降了24.64 kW和62.81 kW。这一结果凸显了WCGAN在基线负荷估测领域的高精度特性。WCGAN的MAPE比GCN和平均法分别降低了7.46% 和20.46%。其他指标也有显著降低。这进一步验证了WCGAN在估测精确度方面的显著优势。
另外,WCGAN通过对影响因素的高度筛选,能够自动识别并选择与需求响应日最为相近的未响应日负荷曲线作为生成过程的参考,从而产生与真实值高度接近的估测结果。这一过程显著提高了估测的精确度。
仅使用2022年8月数据作为数据集,3种方法的预测结果和误差如表 3所示。评价指标结果如表 4所示。
表 3
8月数据集下3种方法的预测结果和误差
| 时刻 | 真实值 | WCGAN | GCN | 平均法 | |||||
| 预测结果 | 误差 | 预测结果 | 误差 | 预测结果 | 误差 | ||||
| 12:15 | 565.2 | 592.0 | 26.8 | 598.8 | 33.6 | 541.4 | 23.8 | ||
| 12:30 | 502.0 | 537.6 | 35.6 | 580.8 | 78.8 | 549.3 | 47.3 | ||
| 12:45 | 454.0 | 394.8 | 59.2 | 513.2 | 59.2 | 579.2 | 125.2 | ||
| 13:00 | 483.2 | 524.0 | 40.8 | 557.6 | 74.4 | 571.9 | 88.7 | ||
| 13:15 | 470.0 | 527.2 | 57.2 | 529.6 | 59.6 | 524.8 | 54.8 | ||
| 13:30 | 401.6 | 359.2 | 42.4 | 347.2 | 54.4 | 490.6 | 89.0 | ||
| 13:45 | 355.2 | 420.4 | 65.2 | 286.0 | 69.2 | 441.4 | 86.2 | ||
| 14:00 | 302.0 | 367.2 | 65.2 | 396.4 | 94.4 | 407.5 | 105.5 | ||
| 14:15 | 276.8 | 308.4 | 31.6 | 326.0 | 49.2 | 353.8 | 77.0 | ||
| 14:30 | 294.0 | 344.4 | 50.4 | 255.2 | 38.8 | 400.5 | 106.5 | ||
| 14:45 | 317.6 | 306.8 | 10.8 | 278.8 | 38.8 | 376.7 | 59.1 | ||
| 15:00 | 359.2 | 316.0 | 43.2 | 313.6 | 45.6 | 436.8 | 77.6 | ||
| 15:15 | 554.8 | 487.2 | 67.6 | 521.2 | 33.6 | 559.9 | 5.1 | ||
| 15:30 | 653.2 | 690.8 | 37.6 | 617.6 | 35.6 | 620.4 | 32.8 | ||
| 15:45 | 769.2 | 714.4 | 54.8 | 705.2 | 64.0 | 617.2 | 152.0 | ||
| 16:00 | 756.8 | 693.6 | 63.2 | 668.0 | 88.8 | 620.8 | 136.0 | ||
由表 3和表 4可知:WCGAN与GCN估计结果的差异显著减小;WCGAN的估计精度出现大幅度下降,与GCN之间的性能差距显著缩小。主要原因是WCGAN在进行估计时,对数据量的需求远高于GCN及其他算法。WCGAN依赖于大量数据进行细致筛选,以确保估计精度。在数据量显著受限时,WCGAN的精度优势就没有那么明显了。
表 4
8月数据集下3种方法的评价指标结果
| 指标 | RMSE/MW | MAPE/% | MPB/% | MAE/MW | MRPE/% |
| WCGAN | 49.52 | 10.84 | 2.50 | 46.98 | 10.50 |
| GCN | 60.46 | 13.41 | 0.57 | 57.38 | 13.27 |
| 平均法 | 25.05 | 25.05 | 12.92 | 79.19 | 16.17 |
3.3 基于WCGAN和GCN的响应潜力预测算例
3.3.1 基于WCGAN的基线负荷预测
3.3.2 基于GCN的响应负荷预测
3.3.3 响应潜力预测
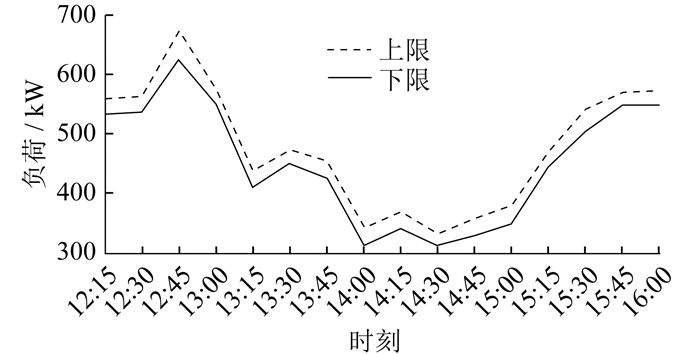
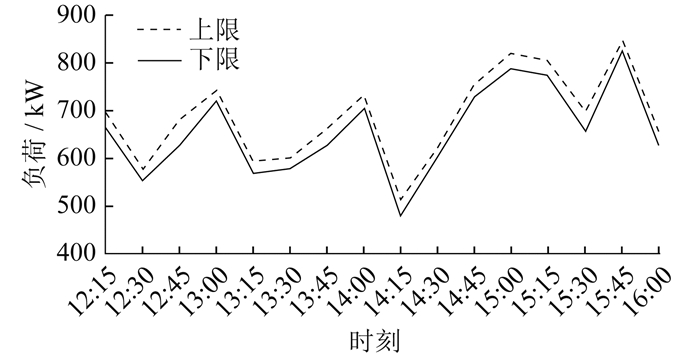
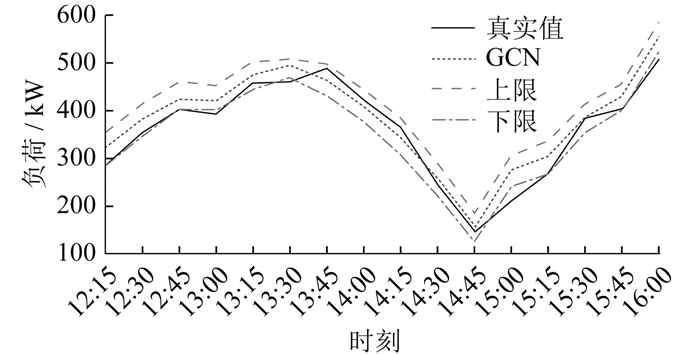
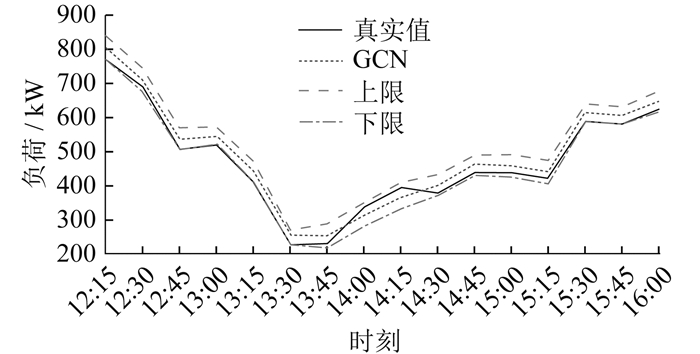
结合基线负荷和响应负荷曲线,得到该用户2022年8月15日和8月18日的整体响应潜力预测结果区间如表 5所示。
表 5
整体响应潜力预测结果
| 日期 | 数据类别 | 响应容量/kWh | 平均响应速度/kW | 最大响应幅度/kW | 响应可信度/% |
| 8月15日 | 预测上限 | 521.6 | 130.4 | 277.1 | 260.80 |
| 预测下限 | 155.6 | 38.9 | 175.7 | 77.78 | |
| 预测平均值 | 340.5 | 85.1 | 232.1 | 170.24 | |
| 真实值 | 400.0 | 100.0 | 277.6 | 200.00 | |
| 8月18日 | 预测上限 | 914.4 | 228.6 | 450.0 | 914.43 |
| 预测下限 | 548.4 | 137.1 | 355.5 | 548.38 | |
| 预测平均值 | 733.3 | 183.3 | 402.5 | 733.30 | |
| 真实值 | 791.7 | 100.0 | 409.6 | 791.70 |
由表 5可以看出,本文预测响应潜力上下限差值最大的指标是响应可信度。究其原因在于本文使用的WCGAN和GCN在生成预测结果时存在一定数值的偏移,而且这一偏移仅由预测方法的精度决定。
4 结语
本文提出了一种基于改进CGAN的灵活性资源响应潜力预测方法。与传统K-means聚类法或支持向量机回归法等相比,WCGAN有效克服了由大数据量和多影响因素引起的梯度消失和模式崩溃问题。本文还引入了一种考虑双重不确定性的预测方法,该方法显著提高了灵活性资源响应潜力预测的准确性,对于优化电网需求响应资源调度和增加电力用户利润具有重要意义。
参考文献
-
[1]宋振培, 张少迪, 周品品. 基于需求响应的电力负荷预测与建模研究[J]. 上海电力大学学报, 2024, 40(1): 51-57.
-
[2]董佳瑜, 王辉, 赵文会, 等. 考虑空调负荷响应潜力的配电网电力弹性平衡方法[J]. 上海电力大学学报, 2023, 39(3): 219-225.
-
[3]ZHANG L Y, LI G F, HUANG Y X, et al. Distributed baseline load estimation for load aggregators based on joint FCM clustering[J]. IEEE Transactions on Industry Applications, 2023, 59(1): 567-577. DOI:10.1109/TIA.2022.3208874
-
[4]ZHANG Y F, WU Q W, AI Q, et al. Closed-loop aggregated baseline load estimation using contextual bandit with policy gradient[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 243-254. DOI:10.1109/TSG.2021.3112611
-
[5]刘春阳, 李康平, 纪陵, 等. 基于聚类-估计联动的需求响应集群基线负荷估计方法[J]. 电力系统自动化, 2023, 47(2): 79-87.
-
[6]林琳, 高雪, 甄钊. 居民用户的需求响应基线负荷估计[J]. 电气自动化, 2022, 44(1): 63-66.
-
[7]付文杰, 王喻玺, 申洪涛, 等. 基于拉丁超立方抽样和场景消减的居民用户基线负荷估计方法[J]. 电网技术, 2022, 46(6): 2298-2307.
-
[8]申洪涛, 刘宝铭, 任鹏, 等. 基于辨识解耦的含高渗透分布式光伏用户集群基线负荷估计方法[J]. 电力系统保护与控制, 2022, 50(3): 164-173.
-
[9]LI K P, WANG Y X, ZHANG N, et al. Precision and accuracy co-optimization-based demand response baseline load estimation using bidirectional data[J]. IEEE Transactions on Smart Grid, 2023, 14(1): 266-276.
-
[10]ZHANG Y F, AI Q, LI Z Y. Improving aggregated baseline load estimation by Gaussian mixture model[J]. Energy Reports, 2020, 6(S9): 1221-1225.
-
[11]GE X X, XU F, WANG Y X, et al. Spatio-temporal twodimensions data based customer baseline load estimation approach using LASSO regression[J]. IEEE Transactions on Industry Applications, 2022, 58(3): 3112-3122.
-
[12]俱鑫, 刘尚科, 苟瑞欣, 等. 基于ARMA和Kalman Filter的需求响应基线负荷预测[J]. 电子设计工程, 2020, 28(18): 175-180.
-
[13]TAO P, XU F, DONG Z B, et al. Graph convolutional network-based aggregated demand response baseline load estimation[J]. Energy, 2022, 251: 123847.
-
[14]蒋正威, 张锋明, 胡凤桐, 等. 虚拟电厂分布式资源的聚合响应能力评估方法[J]. 电力工程技术, 2022, 41(6): 39-49.
-
[15]王樊云, 刘敏, 李庆生, 等. 新型电力系统下电力用户的需求响应潜力评估[J]. 电测与仪表, 2023, 60(8): 105-113.
-
[16]郭朝波, 张溢波, 张宏炯, 等. 粗糙模糊环境下电力用户负荷响应潜力评估[J]. 中国电力, 2023, 56(11): 134-142.
-
[17]朱明辉, 权琛, 朱超, 等. 耦合聚类基线及舒适度的居民负荷需求响应评估方法[J]. 电网与清洁能源, 2023, 39(5): 99-105.
-
[18]叶尔森·赛里克, 杨希, 李美颐, 等. 基于集成学习的负荷聚合商需求响应潜力概率预测模型[J/OL]. 电测与仪表: 1-9[2024-01-26]. http://kns.cnki.net/kcms/detail/23.1202.TH.20230214.0955.004.html.
-
[19]吴迪, 王韵楚, 郁春雷, 等. 基于高斯过程回归的工业用户需求响应潜力评估方法[J]. 电力自动化设备, 2022, 42(7): 94-101.
-
[20]林珊, 王红, 齐林海, 等. 基于条件生成对抗网络的短期负荷预测[J]. 电力系统自动化, 2021, 45(11): 52-60.
-
[21]卢俊菠, 刘俊峰, 罗燕, 等. 基于改进WGAN考虑特征分布相似性的小样本负荷预测方法[J/OL]. 控制理论与应用: 1-11[2023-10-31]. http://kns.cnki.net/kcms/detail/44.1240.tp.20230324.1740.017.html.
-
[22]黄海荣, 吴君, 郁丹, 等. 基于经验模态条件生成对抗网络的短期负荷预测[J]. 自动化仪表, 2022, 43(12): 25-29.
-
[23]周柏润, 孙伟, 魏敏捷, 等. 基于卷积神经网络的电力信息物理融合系统入侵检测方法研究[J]. 上海电力大学学报, 2023, 39(2): 117-122.