|
|
|
发布时间: 2024-08-28 |
新能源发电技术 |
|
|
|
收稿日期: 2024-03-03
中图法分类号: TM464
文献标识码: A
文章编号: 2096-8299(2024)04-0325-06
|
摘要
针对海上风电集群经多端柔直并网时的次同步振荡(SSO)频发问题,提出了一种基于Weibull分布模型和带漏项最小均方算法的SSO概率评估方法,分析了大容量直驱风机集群经柔直并网引起的SSO变化特性。仿真结果表明:风速增加使SSO频率由40 Hz下降至18 Hz附近,负阻尼比累计概率由14%增至90%;构成风电场的等值风机台数增加与多端柔直并网可以扩展SSO频率分布区间,并降低1%~8%的SSO负阻尼比累计概率。
关键词
直驱风机; 柔直输电; 次同步振荡; 小信号建模
Abstract
Addressing frequent sub-synchronous oscillations (SSO) in multi-terminal VSCHVDC integrated offshore wind clusters, a probabilistic assessment method using the Weibull distribution and a Leaky Least Mean Squares algorithm is proposed to explore SSO dynamics in large-capacity direct-drive wind farms. Findings reveal that increased wind speeds shift SSO frequencies from 40 Hz to around 18 Hz, and the cumulative probability of negative damping ratios rises from 14% to 90%. More turbines and multi-terminal integration expand the SSO frequency range and reduce negative damping cumulative probabilities by 1%~8%, offering guidance for large-scale offshore wind integration.
Key words
permanent magnet synchronous generator; flexible direct current transmission; sub-synchronous oscillation; small-signal modeling
基于电压源变换器的高压直流传输(Voltage Source Converter-based High Voltage Direct Current,VSC-HVDC)技术的远距离海上风电外送具有电能质量好、灵活性高等优点[1]。随着海上风电场群的连片开发,两端柔直系统已经很难满足多主网落点及多个海上风电场的接入要求[2]。海上风电场群经基于电压源变换器的多端直流输电(Voltage Source Converter-based Multi-Terminal Direct Current,VSC-MTDC)系统并入陆上电网的接入方式成为一种新趋势。然而,多端柔直输电系统出现的次同步振荡(Sub-Synchronous Oscillation,SSO)现象[3]是制约海上风电发展的主要障碍之一。永磁同步风机(Permanent Magnet Synchronous Generator,PMSG)较双馈风机具有更高的可靠性。研究含PMSG的多端柔直输电系统SSO机理,掌握其概率评估方法,可以为远海风电场集群的电能传输提供技术支撑[4]。
为了从不同角度揭示SSO机理,文献[5]建立了并网系统的小信号模型,分析了SSO的稳定特性。文献[6]采用阻抗建模法,结合奈奎斯特判据,分析了风电场经模块化多电平换流器系统并网的宽频振荡机理。文献[7]借助小信号模型与直驱机组运行特性曲线,研究了不同运行区域的SSO特性与桨距角对SSO的作用机理。文献[8]基于独立通道理论,将多输入、多输出并网系统转化为单输入、单输出系统,定性分析了不同控制通道的SSO交互作用程度。上述文献对于含PMSG的多端柔直并网系统研究较少,且主要针对确定性运行场景的振荡机理进行分析,没有结合风速这一不确定因素进行SSO机理研究。
本文通过建立大容量直驱风机集群经多端柔直并网系统的小信号模型,计算SSO频率和阻尼比,并结合参与因子法分析其主要振荡模态。首先,使用蒙特卡罗(Monte Carlo)抽取风速的威布尔(Weibull)分布模型生成随机风速点;其次,采用带漏项的最小均方(Leaky Least Mean Squares,Leaky LMS)算法量化风速、频率、阻尼比的概率密度分布;最后,通过算例研究风速、风机台数和并网形式对SSO频率和阻尼比的概率密度分布影响,得到含PMSG的多端柔直输电系统的SSO变化特性。
1 PMSG集群经VSC-MTDC并网系统模型
1.1 小信号建模与验证
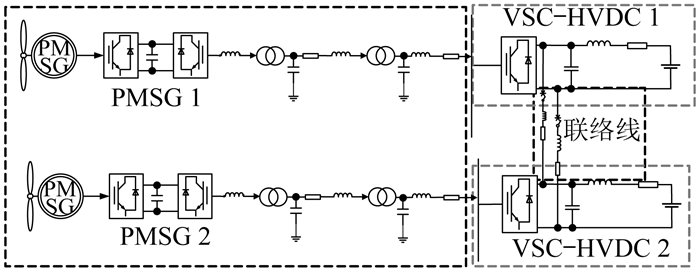
本文根据PMSG与换流站HVDC参数[9]构建海上风电场并网系统。PMSG集群经VSC-HVDC多端并网系统结构如图 1所示。
系统由PMSG1和PMSG2两个风电场通过换流站并入陆上电网,换流站VSC-HVDC1和VSC-HVDC2之间通过设置联络线改变风电场的并网形式,联络线断开时为两端柔直并网系统。为便于分析,将系统分为PMSG系统和VSC-HVDC系统。其中,PMSG风电场由50台风机采用单机等值法构成;由于柔直环节具有解耦作用且陆上电网较强,受端换流器可等效为恒定直流电压源[10]。各系统的动态方程[11]联立得到本文所建立的小信号模型:
| $ \begin{equation*} \frac{\mathrm{d}}{\mathrm{d} t} \Delta \boldsymbol{X}=\boldsymbol{A} \Delta \boldsymbol{X}+\boldsymbol{B} \Delta \boldsymbol{U} \end{equation*} $ | (1) |
式中:
在软件PSCAD中搭建对应的时域模型验证小信号建模的准确性。在2 s时令风速分别由5 m/s上升至7~15 m/s,使用Prony算法分析各风速工况下的风电场功率输出波形,得到SSO频率fSSO'和阻尼比ζ,将根据式(1)计算的SSO频率记为fSSO,DfSSO表示fSSO与fSSO'的差值。小信号建模与Prony算法的SSO计算结果比较如表 1所示。
表 1
小信号建模与Prony算法的SSO计算结果比较
| 风速(/m/s) | f'sso | fsso | |Δfsso | | ζ |
| 7 | 23.571 7 | 23.491 4 | 0.080 3 | 0.971 8 |
| 9 | 21.562 0 | 20.105 0 | 1.457 0 | 0.371 3 |
| 12 | 19.211 5 | 18.768 9 | 0.442 6 | −0.876 1 |
| 15 | 18.176 4 | 18.596 6 | 0.420 2 | −1.382 8 |
由表 1可知,两种模型的振荡分析结果基本一致,验证了所建数学模型的准确性。同时,随着平均风速的增加,系统阻尼比呈现下降趋势,由正阻尼比变为负阻尼比,表明系统存在SSO风险。
1.2 PMSG集群经VSC-MTDC并网系统的稳定性分析
通过潮流计算求解各状态变量初值后,采用特征值法计算式(1)的小信号模型,可得PMSG集群经VSC-MTDC系统的振荡模式,如表 2所示。
表 2
PMSG集群经VSC-MTDC系统的振荡模式
| 振荡模式 | 特征值 | 振荡频率/Hz | 阻尼比/% |
| 1 | 7.582±131.572i | 20.940 | −5.800 |
| 2 | −5.253±135.858i | 21.622 | 3.900 |
| 3 | −0.688±44.368i | 7.061 | 0.015 |
| 4 | −0.654±122.728i | 19.533 | 0.500 |
| 5 | 0.537±265.660i | 42.281 | −0.200 |
| 6 | −0.426±145.112i | 23.095 | 0.300 |
| 7 | −0.362±155.431i | 24.738 | 0.200 |
| 8 | −0.297±23.837i | 3.794 | 1.200 |
| 9 | −0.066±11.784i | 1.875 | 0.600 |
由表 2可知,系统中主要存在9种振荡模式,其中振荡模式1和5为负阻尼,表示系统存在振荡风险。考虑到振荡模式1的阻尼比最小,对该振荡模式进行归一化处理并分析参与因子。SSO模式下各状态变量的参与因子如图 2所示。
由图 2可知,振荡模式1受风电场影响较多,参与因子udci、x4i、x5i、idgi(i=1,2)对应状态变量为风电场直流电压、网侧换流器电压外环与电压内环d轴比例积分增益系数、网侧换流站及出口d轴电流分量。由于影响因素为风速、风机台数、滤波电感和集结线参数,且考虑到针对内部因素影响SSO特性的分析相对成熟,本文将围绕风速、风机台数、并网形式等外部因素进行分析。
2 SSO概率评估方法
基于构建的小信号模型,引入风速概率分布模型,采用Leaky LMS算法拟合风速与SSO频率及阻尼比的概率密度分布。
相较于伽马、瑞利等风速分布模型,本文选用的Weibull分布适用的风速分布特征种类更加丰富,计算较为简单[12]。典型的双参数Weibull分布适用的风速分布特征种类更加丰富,计算较为简单[12]。典型的双参数Weibull分布概率密度函数为
| $ \left\{\begin{array}{l} f(\mu, k, \lambda)=\frac{k}{\lambda}\left(\frac{\mu}{\lambda}\right)^{k-1} \mathrm{e}^{-\left(\frac{\mu}{\lambda}\right)^{k}}, v \geqslant 0 \\ k=\left(\frac{D}{v}\right)^{-1.068} \\ \lambda=\frac{v}{\Gamma\left(1+k^{-1}\right)} \end{array}\right. $ | (2) |
式中:
对式(2)进行积分,得到Weibull分布的累计分布函数为
| $ \begin{equation*} F(v, k, \lambda)=1-\mathrm{e}^{-(v / \lambda)^{k}} \end{equation*} $ | (3) |
根据Monte Carlo定义,生成服从[0, 1]区间的均匀分布随机数ξi,并将其代入式(3),得到的风速抽样样本νm为
| $\begin{equation*} v_{m}=\lambda\left[-\ln \left(\xi_{i}\right)\right]^{k} \end{equation*} $ | (4) |
基于Leaky LMS算法拟合风速与SSO频率、阻尼比关系,计算公式为
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}(k)=\hat{\boldsymbol{\theta}}(k-1)+\alpha e(k) \boldsymbol{h}(k)-\gamma \hat{\boldsymbol{\theta}}(k-1) \\ e(k)=z(k)-\boldsymbol{h}^{\mathrm{T}}(k) \hat{\boldsymbol{\theta}}(k-1) \end{array}\right. $ | (5) |
式中:
为了平衡算法的收敛速度与稳定性,设
通过特征值得出关注风速下的SSO频率(vm,fssoi)和阻尼比(vm,ζi),其中m = 1,2,3,⋯,k。
拟合函数的系数向量
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}_{f}(k-1)=\left[\theta_{f 1}, \theta_{f 2}, \theta_{\beta 3}, \theta_{f 4}, \theta_{f 5}\right] \\ \hat{\boldsymbol{\theta}}_{\zeta}(k-1)=\left[\theta_{\zeta 1}, \theta_{\zeta 2}, \theta_{\zeta 3}, \theta_{\zeta 4}, \theta_{\zeta 5}\right] \end{array}\right. $ | (6) |
| $\left\{\begin{array}{l} f_{\mathrm{ss} i}=\theta_{f 1} v_{m}^{4}+\theta_{f 2} v_{m}^{3}+\theta_{\beta 3} v_{m}^{2}+\theta_{f 4} v_{m}+\theta_{f 5} \\ \zeta_{i}=\theta_{\zeta 1} v_{m}^{4}+\theta_{\zeta 2} v_{m}^{3}+\theta_{\zeta \zeta} v_{m}^{2}+\theta_{\zeta 4} v_{m}+\theta_{\zeta 5} \end{array}\right. $ | (7) |
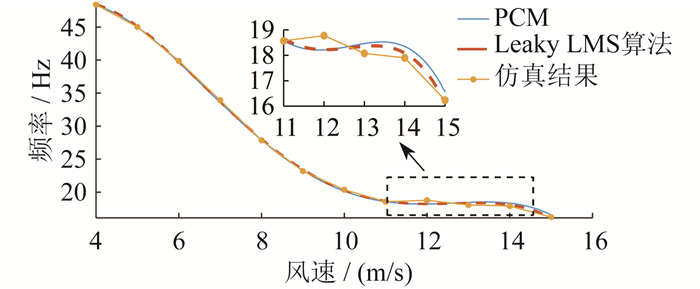
为评估式(7)的拟合准确度,基于图 1中的系统建模,设定风电场风机台数为50台,并建立v = 9 m/s、D = 3的Weibull风速分布模型,从而对比Leaky LMS算法和概率配点法(Probabilistic Collocation Method,PCM)拟合风速和频率的精度。算法拟合与仿真结果对比如图 3所示。
由图 3可知:PCM和Leaky LMS算法在风速小于10 m/s的范围内拟合效果较好,但PCM在风速大于10 m/s时的拟合准确度低于Leaky LMS算法;PCM与Leaky LMS算法的误差平方和分别为1.588、0.567,可见PCM对频率的拟合存在较大误差。综合上述结果可知,本文采用的Leaky LMS算法具有较好的准确性。
3 算例分析
3.1 风速和并网结构对SSO的影响分析
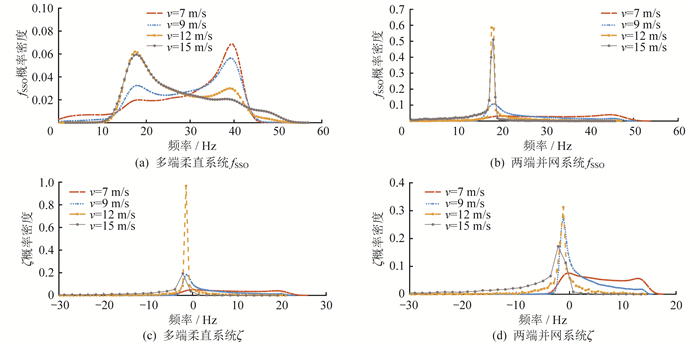
PMSG风电集群经柔直并网时fSSO和ζ的概率密度分布如图 4所示。
由图 4(a)可知,多端柔直并网系统中fSSO的概率密度分布范围为1.61~56.84 Hz,随着v由7 m/s增大到15 m/s,SSO频率峰值点从39.77 Hz、0.068 6变为17.79 Hz、0.059 6,风速增大使fSSO的概率密度分布重心从较大频率区域向较小频率区域移动。由图 4(b)可知,两端柔直并网系统中fSSO的概率密度分布范围在0.16~50.61 Hz,fSSO峰值点坐标随着v的增大由44.63 Hz、0.039 7变为18.61 Hz、0.509 9,fSSO随风速增大而降低,但在高风速环境中,fSSO的概率密度分布集中于18.61 Hz附近区域。由图 4(c)、图 4(d)可知:风速对不同并网拓扑下ζ的概率密度分布也具有中心区域大于边缘区域的特性;多端柔直并网系统中ζ的概率密度分布范围为−29.81%~28.19%,随着风速增大,ζ的概率密度分布峰值点由1.92%、0.098 9变为−5.08%、0.012 0,由正阻尼变为负阻尼,负阻尼比累计概率由14%增大为90%,SSO风险增加;两端柔直系统中ζ的概率密度分布范围为−40.22%~17.52%;随着风速增大,ζ的概率密度分布峰值向负阻尼区间移动,负阻尼比累计概率由16% 增大至94%,SSO严重程度随风速增加而增加。由此可知,两端并网系统各风速下的负阻尼比累计概率均大于多端柔直系统,说明采用多端柔直并网有利于提高系统稳定性。
3.2 风机台数对SSO分布的影响分析
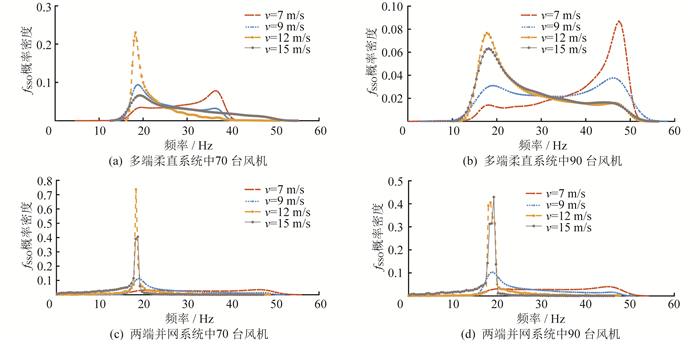
基于上文的分析结果,改变直驱风电场风机台数为70、90台,以分析风机台数对系统SSO特性的影响。风机台数分别为70、90台时,PMSG风电集群经柔直并网时fSSO的概率密度分布如图 5所示。
由图 4(a)、图 4(b)和图 5可知,风机台数主要影响区间所处的位置,不会改变风速对fSSO分布区间的影响。
随着风机台数从50台增至90台,多端柔直系统中fSSO的概率密度分布分布范围由1.61~ 56.84 Hz变为10.3~58.23 Hz,两端柔直系统中fSSO的概率密度分布范围由0.16~50.61 Hz变为0.71~ 53.12 Hz,fSSO分布区间逐渐向右侧移动。
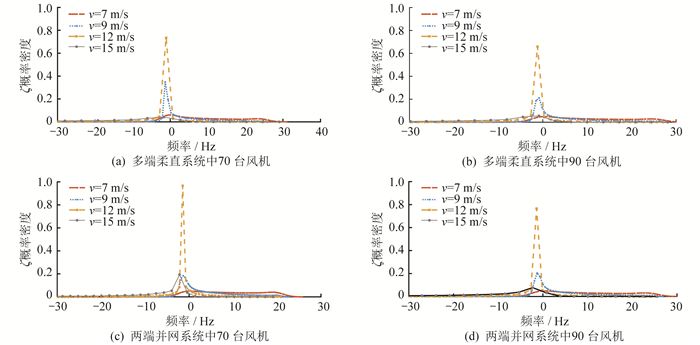
不同风机台数构成的风电集群经柔直并网时ζ的概率密度分布如图 6所示。
由图 4(c)和图 6(a)、图 6(b)可知,在相同风速条件下,当等值风机台数由50台上升为70、90台时,多端柔直系统中ζ的概率密度分布范围由−29.81%~28.19% 变为−32.6%~30.86%、−39.6%~ 32.69%,区间整体向正值区域移动,负阻尼比累计概率降低2%~14%,系统稳定性提升。由图 4 (d)和图 6(c)、图 6(d)可知,两端柔直系统中ζ的概率密度分布范围由− 40.22%~17.52%,变为−39.78%~26.83%、−30.23%~29.24%,向正值区域移动,负阻尼比累计概率降低1%~8%,系统稳定性有所提升,但低于多端柔直并网系统的稳定性提升。因此,增加风机台数与采用多端柔直并网可以降低负阻尼比累计概率1%~14%、1%~8%,减弱SSO严重程度。
4 结论
本文提出基于Leaky LMS算法的PMSG集群经VSC-MTDC并网的SSO概率评估方法,从风速、风机台数、风场并网形式等方面研究了SSO机理,得到如下结论。
(1) SSO频率分布重心随风速的增大向小值区域移动;增加风机台数与多端柔直并网使得SSO频率分布区间向大值区间移动。
(2) 随着平均风速的增大,负阻尼比累计概率逐渐由12% 增至80% 附近,系统稳定性减弱;在相同风速与并网形式下,增加风机台数可以降低负阻尼比累计概率1%~14%,减弱SSO严重程度;在相同风速与风机台数下,PMSG经VSCMTDC并网系统较VSC-HVDC系统的负阻尼比累计概率降低1%~8%,系统的稳定性更优。
参考文献
-
[1]任必兴, 孙蓉, 李强, 等. 经柔性直流接入的大规模直驱风电场等效建模与小干扰稳定性分析[J]. 电力自动化设备, 2022, 42(5): 142-152.
-
[2]朱介北, 史美琦, 索之闻, 等. 基于直流电压补偿的海上风电-多端柔直送出系统惯量协调控制[J/OL]. 电网技术: 1-14[2024-02-10]. https://doi.org/10.13335/j.1000-3673.pst.2023.0388.
-
[3]雷傲宇, 汪林光, 梅勇, 等. 多端柔性直流电网的中高频振荡特性分析[J]. 电网与清洁能源, 2023, 39(7): 54-60.
-
[4]张志强, 李秋彤, 余浩, 等. 海上直驱风电经柔直并网系统的次/超同步振荡特性分析[J]. 上海交通大学学报, 2022, 56(12): 1572-1583.
-
[5]鲁晓军, 向往, 林卫星, 等. 混合型模块化多电平换流器小信号模型及其小信号稳定性研究[J]. 中国电机工程学报, 2019, 39(24): 7286-7298.
-
[6]吕敬, 蔡旭, 张占奎, 等. 海上风电场经MMC-HVDC并网的阻抗建模及稳定性分析[J]. 中国电机工程学报, 2016, 36(14): 3771-3781.
-
[7]赵书强, 沈俊铃, 邵冰冰. 直驱风电场经柔直并网系统全运行区域次同步振荡特性分析[J]. 太阳能学报, 2021, 42(12): 163-173.
-
[8]张芳, 王赫, 李传栋. 含静止无功发生器的直驱风电并网系统稳定性分析及振荡抑制策略[J/OL]. 电力自动化设备: 1-9[2024-02-10]. https://doi.org/10.16081/j.epae.202310005.
-
[9]李思妍. 直驱风电场经多端柔性直流输电并网系统振荡特性分析[D]. 北京: 华北电力大学, 2022.
-
[10]吕敬, 蔡旭. 提高风场柔直并网系统稳定性的控制器参数优化设计[J]. 中国电机工程学报, 2018, 38(2): 431-443.
-
[11]邵冰冰. 直驱风电场经柔直并网系统的振荡特性和抑制策略研究[D]. 北京: 华北电力大学, 2021.
-
[12]廖坤玉. 双馈风电系统时变间谐波的解析建模及其谐振特性研究[D]. 北京: 华北电力大学, 2019.
-
[13]KAMENETSKY M, WIDROW B. A variable Leaky LMS adaptive algorithm[C]//Conference Record of the ThirtyEighth Asilomar Conference on Signals, Systems and Computers. CA, USA: ASSC, 2004: 125-128.
-
[14]陈武晖, 王丹辉, 宿端鹏, 等. 双馈风电场感应发电机效应的安全风险评估方法[J]. 电网技术, 2017, 41(3): 854-862.