|
|
|
发布时间: 2024-08-28 |
新能源发电技术 |
|
|
|
收稿日期: 2024-04-12
基金项目: 上海市教育委员会科研创新计划项目(2021-01-07-00-07-E00122)
中图法分类号: TM315
文献标识码: A
文章编号: 2096-8299(2024)04-0331-09
|
摘要
针对海上风电机组部件故障关联作用的不确定性量化及维护策略优化问题,提出了一种考虑故障关联不确定性的海上风电机组预防性维护策略优化方法。首先,采用区间分析方法对故障关联不确定性进行量化,引入区间故障关联系数描述故障关联的不确定性对机组部件可靠度的影响。其次,根据部件运行状态信息,利用神经网络捕捉故障关联图的时空特征,构建基于图注意力-门控循环单元神经网络(GAT-GRU)的故障关联预测模型,形成区间故障关联系数矩阵。最后,以维护费用最低为目标函数,部件可靠性指标为约束条件,构建了考虑故障关联不确定性的联合维护模型,优化各部件的预防性维护时间区间。算例仿真结果验证了所提方法的有效性和经济性。
关键词
海上风电机组; 故障关联; 不确定性; 区间分析法; 神经网络; 预防性维护
Abstract
Aiming at the problem of uncertainty quantification and maintenance decisionmaking of the failure correlation effects of offshore wind turbine components, an optimisation method of preventive maintenance strategy for offshore wind turbines considering the failure correlation uncertainty is proposed. Firstly, the interval analysis method is used to quantify the uncertainty of failure correlation, and the failure correlation interval model is constructed to obtain the reliability interval of components under the influence of uncertainty. Secondly, according to the running state information of the components, the neural network is used to capture the spatiotemporal characteristics of the fault correlation graph, and a fault correlation prediction model based on GAT-GRU is constructed to form an interval fault correlation coefficient matrix.Finally, taking the minimum maintenance cost as the goal and the component reliability index as the constraint, a preventive maintenance model considering the uncertainty of fault correlation is constructed to optimize the preventive maintenance time interval of each component. The simulation results verify the effectiveness and economy of the proposed method.
Key words
offshore wind turbine; failure correlation; uncertainty; interval analysis method; neural network; preventive maintenance strategy
海上风电是推进我国能源结构转型、保障能源安全的重要战略支撑之一[1-2]。截至2023年底,我国海上风电累计并网装机量为3 650万kW,同比增长19.8%[3]。随着风电并网容量不断提升,机组的维护需求日益突出。与陆上风机相比,海上风电机组运行维护成本较高,约占生命周期成本的25% 以上[4]。在风电平价上网的背景下,如何实现经济、高效维护,降低用电成本,成为海上风电行业亟待解决的关键问题之一。
作为复杂的多部件系统,海上风电机组部件之间存在3种不同的关联关系,即经济关联、结构关联和故障关联[5]。在故障关联的作用下,传统维护理论中对部件退化的独立性假设不再适用[6-9]。针对故障关联下风电机组的维护决策问题,国内外学者主要从部件故障率相互影响的角度进行了研究。文献[10]利用故障率交互模型对部件间的复杂故障关系进行了描述,并构建机会维护模型,优化了风电机组维护间隔。文献[11]针对风电机组运行期间子系统内部耦合作用和外部环境冲击两种情况下存在的问题,建立了同时考虑故障相关和外部冲击的机会维护策略。文献[12]基于PageRank算法计算风机子系统的被影响度,建立了考虑故障相关性的风电机组状态机会维修模型和定期维修模型。文献[13]采用Copula函数描述风机关键部件的联合风险度,构建了以风险度约束为纽带的双层机会维护模型。文献[14]采用风险因子描述了风机故障对子系统的影响,并利用风险因子优化维护决策,验证了风电机组维护决策时考虑故障关联的必要性。上述研究在对风电机组故障关联建模时,通常假设系统中的故障关联恒定不变,通过拟合得到一个固定的关联系数并指导维护决策,尚未考虑故障关联的不确定性影响。在海上风电机组运行过程中,由于受部件状态等不确定因素影响,关联影响具有不确定性,因此若忽略故障关联的不确定性,可能导致维护策略难以达到最优。
针对此问题,本文提出了一种考虑故障关联不确定性的海上风电机组预防性维护策略优化方法。首先,采用区间分析方法对故障关联的不确定性进行量化,引入区间关联系数描述故障关联不确定性对于部件可靠度的影响。其次,基于故障关联图理论提出一种图注意力-门控循环单元(Graph Attention-Gated Recurrent Unit,GAT-GRU)神经网络的故障关联预测模型,得到机组的区间故障关联系数矩阵。随后,利用区间故障关联系数带来的维护时间区间,对维护时间区间存在重叠的部件进行联合维护,以全生命周期预防维护成本最低为目标函数,部件可靠度为约束条件,构建了考虑故障关联不确定性的预防性维护决策模型。最后,以我国东部某海上风电场机组为例,验证了所提方法的有效性和经济性。
1 基于区间分析方法的机组部件故障关联不确定性建模
机组部件综合故障率模型由两部分组成:部件自身状态退化产生的独立故障率和其余部件故障关联所产生的关联故障率。t时刻部件i的综合故障率λi,co(t)为
| $ \begin{equation*} \lambda_{i, \mathrm{co}}(t)=\lambda_{i}(t)+\sum\limits_{j \neq i} \delta_{j i} \lambda_{j}(t) \end{equation*} $ | (1) |
式中:λi(t),λj(t)——t时刻部件i和部件j的独立故障率;
δji——部件j对部件i的故障关联系数。
由于文献[10]和文献[15]证明了威布尔分布能较好地拟合各部件故障率,所以假设部件独立故障率服从威布尔分布。t时刻部件i的独立故障率λi(t) 和独立可靠度Ri (t)可表示为
| $ \lambda_{i}(t)=\frac{\beta_{i}}{\alpha_{i}}\left(\frac{t}{\alpha_{i}}\right)^{\beta_{i}-1} $ | (2) |
| $ R_{i}(t)=\exp \left[-\int_{0}^{t} \lambda_{i}(t)\right] \exp \left[-\left(\frac{t}{\alpha_{i}}\right)^{\beta_{i}}\right] $ | (3) |
式中:αi,βi——部件i的尺度参数和形状参数。
由于受部件实际运行状态等因素的影响,所以故障关联的精确概率分布确定较难,不恰当的分布函数无法准确反映故障关联的实际变化。关联系数上下界的获取相对来说更容易,只需获得其变化范围,就可对部件故障关联所有可能的状况进行描述。因此,引入区间故障关联系数描述故障关联的不确定性。其公式为
| $\begin{equation*} \left[\delta_{j i}\right]=\left[\underline{\delta_{j i}}, \overline{\delta_{j i}}\right] \end{equation*} $ | (4) |
式中:
部件
| $ \left[\lambda_{i, \mathrm{co}}(t)\right]=\left[\underline{\lambda_{i, \mathrm{co}}}(t), \overline{\lambda_{i, \mathrm{cos}}}(t)\right]=\lambda_{i}(t)+\sum\limits_{j \neq i}\left[\delta_{j i}\right] \lambda_{j}(t) $ | (5) |
式中:
根据式(3)和式(5)可以计算出子系统在故障关联作用不确定影响下的可靠性。部件
| $ \begin{gather*} {\left[R_{i, \mathrm{co}}(t)\right]=\exp \left\{-\int_{0}^{t} \lambda_{i}(t)+\sum\limits_{j \neq i}\left[\delta_{j i}\right] \lambda_{j}(t)\right\}=} \\ R_{i}(t) \prod\limits_{j \neq i}\left[R_{j}(t)\right]^{\left[\delta_{j}\right]} \end{gather*} $ | (6) |
式中:
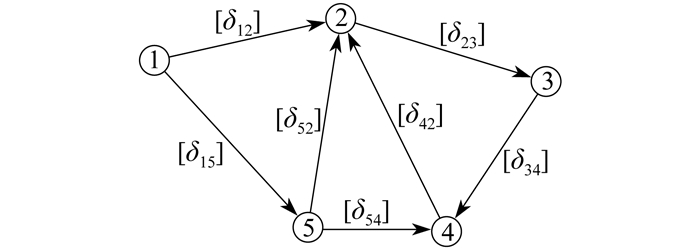
风电机组是一个复杂的多部件系统,故障关联图可以直观表示复杂系统中各部件之间的故障关联关系。引入区间故障关联系数后的风电机组各部件故障关联如图 1所示。其中, 节点(1)、(2)、(3)、(4)、(5)表示系统中的部件; 有向边表示起始部件对箭头所指部件的故障关联作用,即故障关联方向;有向边的权值区间
2 故障关联预测
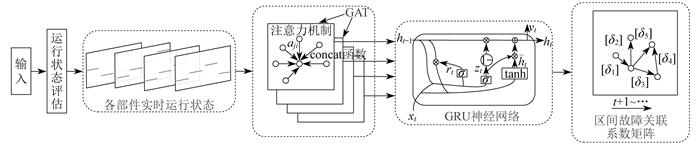
2.1 网络模型整体框架
为了学习和预测风电机组部件间故障关联的不确定性,基于图 1,提出了一种考虑时空相关性的深度学习网络GAT-GRU。该网络将部件的状态信息与机组故障关联网络的拓扑结构相结合。模型整体框架如图 2所示。其中,
首先,输入监视控制与数据采集(Supervisory Control and Data Acquisition,SCADA)系统数据,对各部件的运行状态进行评估;接着,根据评估后的结果,应用图注意力(Graph Attention,GAT)网络衡量部件之间的故障关联程度;随后,利用门控循环单元(Gated Reeurrrent Unit,GRU)神经网络提取故障关联的时间特征,实现故障关联的准确预测;最后,根据预测的故障关联变化程度形成区间故障关联系数矩阵。
2.2 基于GAT网络的故障关联程度评估
图神经网络在处理图数据时能够充分利用图的拓扑结构和节点特征,有效联系不同节点间的特征信息,提高模型的训练和推理速度。注意力机制的基本思想是基于现有的数据挖掘其潜在的相关性,捕捉各节点之间特征和结构的相似性,从而表示节点之间特征更新的贡献程度[15]。因此,借助图神经网络良好的特征提取能力,将部件视为网络中的节点,利用注意力机制衡量部件关联的程度,通过动态注意力权重的上下界形成故障关联系数区间,以表示故障关联的不确定性。
GAT网络的输入
| $ \begin{equation*} \boldsymbol{V}=\left\{\boldsymbol{v}_{1}, \boldsymbol{v}_{2}, \boldsymbol{v}_{3}, \cdots, \boldsymbol{v}_{i}, \cdots, \boldsymbol{v}_{N}\right\} \end{equation*} $ | (7) |
式中:
对于部件
| $ \begin{equation*} \alpha_{j i}=\frac{\exp \left\{\operatorname{LeakyRELU}\left[s\left(\boldsymbol{w}^{l} \boldsymbol{v}_{i}^{l} \| \boldsymbol{w}^{l} \boldsymbol{v}_{j}^{l}\right)\right]\right\}}{\sum\limits_{j \in N} \exp \left\{\operatorname{LeakyRELU}\left[s\left(\boldsymbol{w}^{l} \boldsymbol{v}_{i}^{l} \| \boldsymbol{w}^{l} \boldsymbol{v}_{j}^{l}\right)\right]\right\}} \end{equation*} $ | (8) |
式中:LeakyRELU——非线性激活函数;
融合邻域信息后部件
| $ \begin{equation*} \boldsymbol{v}_{i}^{l+1}=\sigma\left(\sum\limits_{j \in N} \alpha_{i j} \boldsymbol{w}^{l} \boldsymbol{v}_{j}^{l}\right) \end{equation*} $ | (9) |
式中:
2.3 基于GRU神经网络的故障关联趋势预测
由于风电机组部件之间的故障关联具有变化的时间特征,因此使用对时间序列预测有良好性能的GRU神经网络捕捉故障关联图的时间特征。GRU神经网络是针对梯度问题提出的一种循环神经网络,通过引入重置门和更新门的概念,解决了预测过程中的梯度问题[16]。
重置门
| $ \left\{\begin{array}{c} r_{t}=\sigma\left[W_{\mathrm{r}}\left(h_{t-1}, x_{t}\right)+b_{\mathrm{r}}\right] \\ z_{t}=\sigma\left[W_{\mathrm{z}}\left(h_{t-1}, x_{t}\right)+b_{\mathrm{z}}\right] \\ \tilde{h}_{t}=\tanh \left[W_{\tilde{\mathrm{h}}}\left(r_{t} h_{t-1}, x_{t}\right)\right] \\ h_{t}=\left(1-z_{t}\right) h_{t-1}+z_{t} \tilde{h}_{t} \\ v_{t}=\sigma\left(W_{\mathrm{o}} h_{t}\right) \end{array}\right. $ | (10) |
式中:
2.4 模型评估指标
由于故障关联系数是描述故障关联的中间变量,为了更好地评估预测模型的性能,本文采用平均绝对值误差
| $ E_{\mathrm{MAE}}=\frac{1}{T} \sum\limits_{t=1}^{T}\left|y_{t}-\hat{y}_{t}\right| $ | (11) |
| $ E_{\mathrm{RMSE}}=\sqrt{\frac{1}{T} \sum\limits_{t=1}^{T}\left(y_{t}-\hat{y}_{t}\right)^{2}} $ | (12) |
| $ E_{\mathrm{MAPE}}=\frac{1}{T} \sum\limits_{t=1}^{T}\left(\frac{y_{t}-\hat{y}_{t}}{y_{t}}\right) \times 100 \% $ | (13) |
式中:
3 考虑故障关联不确定性的海上风电机组预防性维护模型
3.1 考虑故障关联不确定性的预防性维护策略
当不考虑故障关联不确定性时,部件
当部件
当部件
部件
引入役龄回退因子
| $ \begin{equation*} t_{i, k+}=\left(1-\eta_{i, k}\right) t_{i, k-} \end{equation*} $ | (14) |
式中:
3.2 预防性维护决策模型
以机组运行周期内总维护成本
| $ \begin{align*} \min C_{\mathrm{m}}\left(R^{\mathrm{p}}\right)= & \sum\limits_{k=1}^{K}\left(C_{k}^{\text {worker }}+C_{k}^{\text {vess }}+C_{k}^{\mathrm{pm}}+\right. \\ & \left.C_{k}^{\text {down }}+C_{k}^{\text {punish }}\right) \end{align*} $ | (15) |
维护人员成本为
| $ \begin{equation*} C_{k}^{\text {worker }}=N_{k} \varPsi T_{\mathrm{m} k} \end{equation*} $ | (16) |
式中:
| $ \begin{equation*} T_{\mathrm{m} k}=\frac{t_{k}^{\mathrm{re}}}{A_{k}} \end{equation*} $ | (17) |
式中:
船只租任成本
| $ \begin{equation*} C_{k}^{\text {vess }}=c_{\mathrm{v}} T_{\mathrm{m} k} \end{equation*} $ | (18) |
式中:
在实施维护策略时,对不同的部件执行预防性维护耗费的成本不同。预防性维护成本
| $ \begin{equation*} C_{k}^{\mathrm{pm}}=\sum\limits_{i \in G_{k}} c_{i}^{\mathrm{pm}} \end{equation*} $ | (19) |
式中:
在不考虑故障的情况下,停机损失成本
| $ \begin{equation*} C_{k}^{\text {down }}=c_{\mathrm{p}} W_{k} \end{equation*} $ | (20) |
式中:
维护条件限制可能会导致部分部件延迟维护,使得部件发生故障的风险增加,需要额外付出一定的惩罚成本。惩罚成本
| $ \begin{equation*} C_{k}^{\text {punish }}=\sum\limits_{i \in G_{k}}\left[C_{i}^{\mathrm{cm}} \int_{T_{k}-\Delta t}^{T_{k}} \lambda_{i}(t) \mathrm{d} t\right] \end{equation*} $ | (21) |
式中:
在确保维护成本最优的同时,还应考虑工作时间约束和可靠度约束。
工作时间约束为一天内维护工作人员总工作时间
| $ \begin{equation*} t_{\mathrm{ad}} \leqslant t_{\max } \end{equation*} $ | (22) |
可靠度约束
| $ \begin{equation*} 0 <R_{i}^{\mathrm{p}} \leqslant 1, \quad i=1, 2, 3, \cdots, n \end{equation*} $ | (23) |
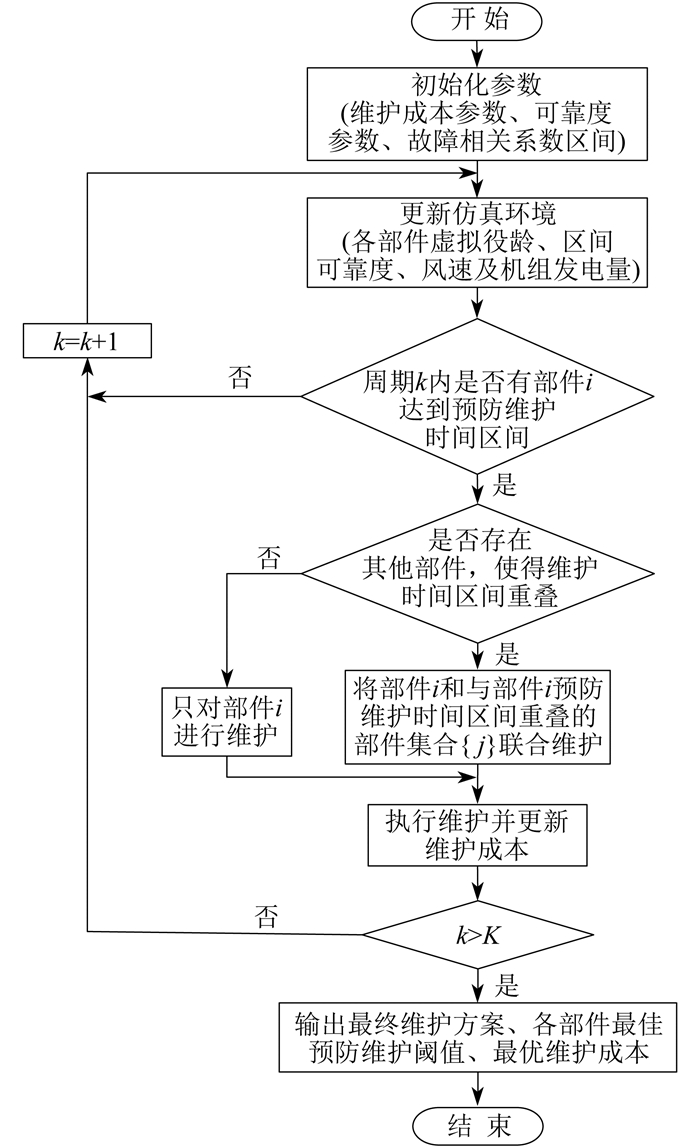
3.3 模型求解
本文提出的考虑故障关联不确定的联合维护模型求解流程如图 5所示。
4 仿真分析
4.1 算例说明
选取我国东部某海上风电场3 MW双馈式风机的齿轮箱、发电机、主轴承和变桨系统等4个关键部件进行算例分析。通过统计各部件实际故障数据,利用MATLAB软件对各部件威布尔分布参数进行拟合,结果如图 6所示。其中,风机的使用寿命为25 a,风电机组切入风速为
各部件的威布尔分布参数和维护成本如表 1所示。
表 1
机组各部件参数
| 部件 | 形状参数 | 尺度参数 | 更换成本/万元 | 不完全维护费用/万元 | 更换时间/h | 不完全维护时间/h |
| 齿轮箱 | 2.445 | 596.3 | 180.00 | 61.74 | 360 | 90 |
| 发电机 | 2.559 | 593.8 | 75.70 | 25.96 | 168 | 42 |
| 主轴承 | 2.012 | 731.7 | 68.50 | 23.50 | 480 | 120 |
| 变桨系统 | 2.855 | 615.2 | 12.33 | 4.22 | 240 | 60 |
4.2 故障关联预测结果
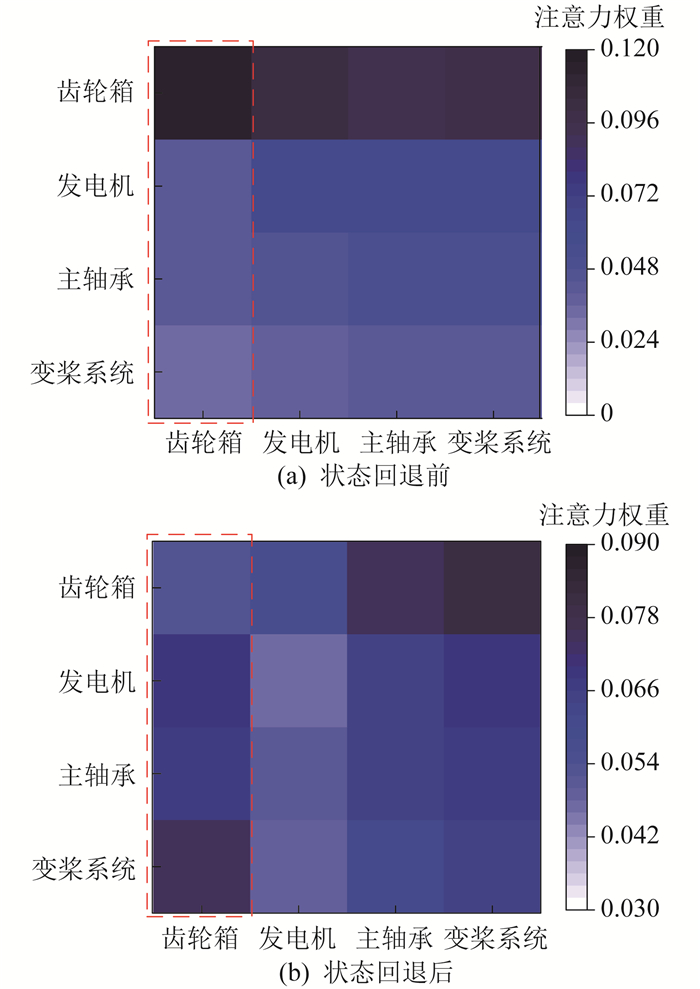
预测模型采用的数据为风电机组4 a状态监测数据。采样周期为10 min,剔除缺失数据后共有190707组数据,使用前3 a的数据进行训练,第4年的数据进行测试。选取部件状态回退作为模型更新的事件,通过注意力权重揭示风电机组部件间关联程度的变化。图 7为某次齿轮箱状态回退前后的注意力权重变化。其中,热力图颜色越深表示权重越大,部件之间关联程度越强。
由图 7(a)可知,齿轮箱维护前,其余部件对齿轮箱影响较小。由图 7(b)可知,齿轮箱状态回退后,其余部件对齿轮箱影响变大。这说明机组部件之间的依赖程度受部件状态影响,当某部件状态较差时,受其余部件的影响程度小;当某部件状态恢复良好时,受其余部件影响程度变大。
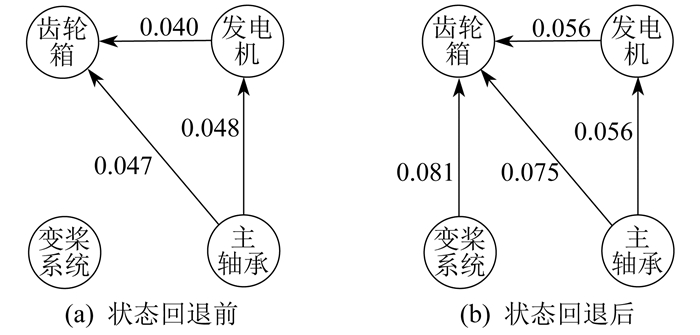
齿轮箱状态回退前后故障关联变化如图 8所示。
由图 8可知,齿轮箱状态回退后其余部件对其影响程度变强,且变桨系统开始影响齿轮箱。
表 2为3种模型的预测误差对比。
表 2
3种模型预测误差对比
| 模型 | EMAE | ERMSE | EMAPE |
| GAT | 0.021 | 0.114 | 0.026 |
| GRU | 0.014 | 0.104 | 0.034 |
| GAT-GRU | 0.007 | 0.082 | 0.011 |
由表 2可知,本文模型精度高于传统GAT模型和GRU模型,在故障关联预测方面表现良好。
变桨系统对发电机的区间故障关联系数为
由图 9可知,
| $[\boldsymbol{\delta}]=\\ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ {[0, 0.118]} & 0 & {[0, 0.070]} & 0 \\ {[0, 0.134]} & {[0, 0.122]} & 0 & {[0, 0.116]} \\ {[0, 0.09]} & {[0, 0.056]} & 0 & 0 \end{array}\right] $ | (24) |
式(24)中,区间矩阵里元素代表部件之间故障关联系数。当故障关联存在不确定性时,其上、下界不同。
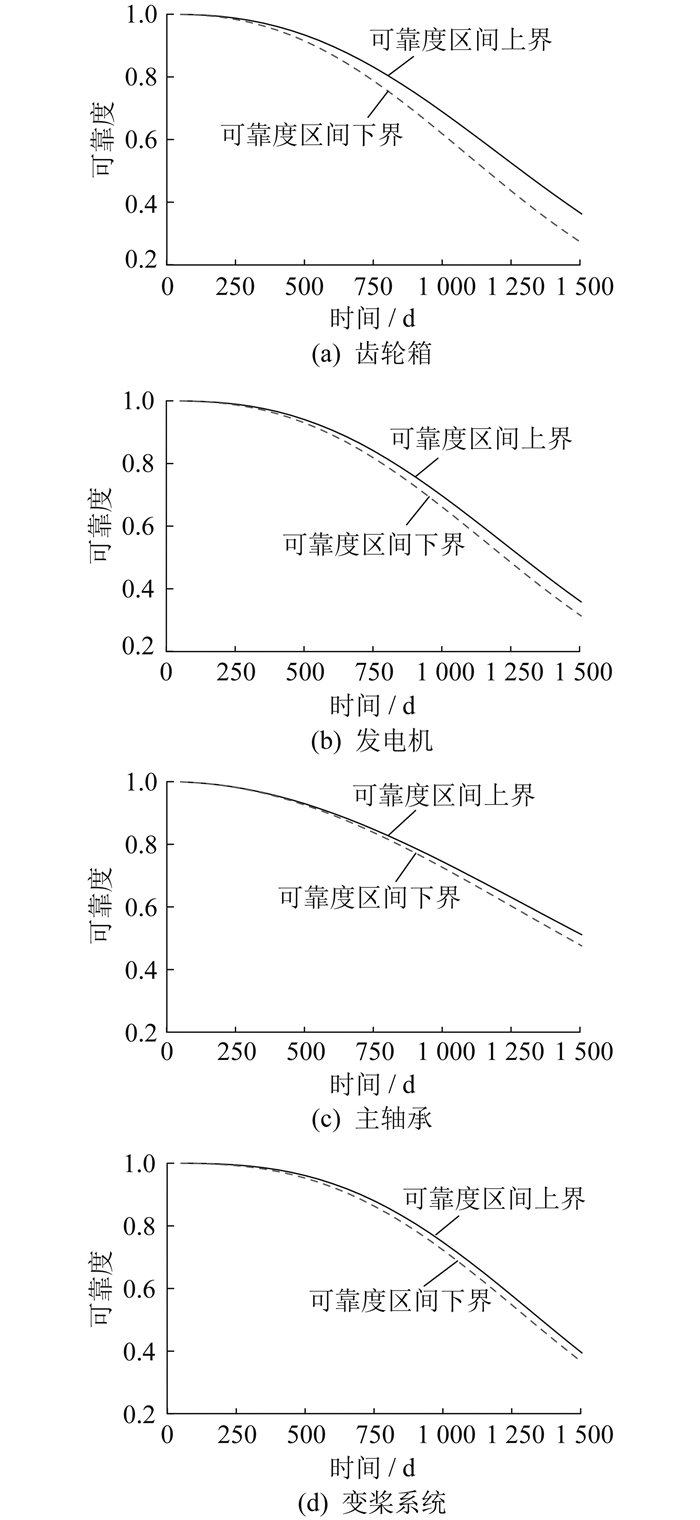
将区间矩阵的上界和下界代入式(6)可得各部件可靠度曲线的下界和上界。各部件可靠度区间如图 10所示。
4.3 维护结果分析
将机组各部件参数带入考虑故障关联不确定性的预防性维护模型,并利用粒子群算法进行优化求解,设置计算时间为25 a。优化后本文所提维护模型的求解结果如表 3所示。
表 3
所提维护模型求解结果
| 部件 | 最优维护阈值Rp | 维护时间区间 |
| 齿轮箱 | 0.850 | [256, 284] |
| 发电机 | 0.856 | [271, 288] |
| 主轴承 | 0.850 | [287, 297] |
| 变桨系统 | 0.882 | [283, 298] |
为了验证所提模型的优越性,在故障相关系数为
表 4
3种方案维护结果对比
| 方案 | 维护总次数 | 维护总成本/万元 | 机组平均可靠度 |
| 1 | [171, 177] | [13 447,13 978] | 0.756 |
| 2 | [75, 83] | [12 480,12 805] | 0.733 |
| 3 | 90 | 12 019.4 | 0.754 |
由表 4可知,在不考虑故障关联不确定性情况下,维护总次数和维护总成本优化结果为区间值。在本文所提的预防性维护策略中,由于考虑到每个部件预防性维护时间的不确定性并根据维护时间区间的重叠部分进行联合维护,故其结果为确定值。
在25 a的运行周期里,方案2与方案1对比,维护总次数减少了88~102次,维护成本降低了4.7%~10.7%,机组平均可靠度降低3%。可见,联合维护虽然能降低维护次数和维护成本,但固定周期的维护策略不能满足实际维护需求,导致机组平均可靠度降低。
方案3与方案2对比,维护总次数增加了7~ 15次,维护总成本降低了3.7%~6.1%,机组平均可靠度提升了2.8%,与方案1相近。可见,考虑故障关联不确定性后,虽然会增加维护次数,但通过优化维护时间区间,合理安排维护计划,使得维护总成本降低,机组可靠度提升。
4.4 灵敏度分析
4.4.1 不确定程度
值得注意的是,当不确定程度为
表 5
不确定程度变化时联合维护中部件数量占比变化
| 不确定性程度 | 2部件占比/% | 3部件占比/% | 4部件占比/% | 单次维护平均部件数/个 |
| 0.6[δ] | 93.8 | 6.2 | 0 | 1.18 |
| 0.8[δ] | 61.4 | 36.6 | 2.0 | 1.61 |
| [δ] | 0 | 100.0 | 0 | 2.00 |
| 1.2[δ] | 42.5 | 29.7 | 27.8 | 2.43 |
| 1.4[δ] | 0 | 4.4 | 95.6 | 3.62 |
| 3[δ] | 0 | 0 | 100.0 | 4.00 |
由表 5可知,随着不确定性程度的增大,多个部件在联合维护中的占比越来越大,维护策略倾向于单次维护修复更多的部件。当不确定程度达到3
4.4.2 天气可及度
5 结论
本文针对海上风电机组的长期预防性维护策略优化问题,基于区间分析方法提出了考虑故障关联不确定性的海上风电机组预防性维护策略,主要结论如下。
(1) 构建了考虑不确定性的部件故障关联模型,利用区间分析方法对不确定性进行量化,对故障关联系数进行区间化处理,描述了部件故障关联的可能情况。
(2) 所提出的GAT-GRU模型通过利用注意力机制衡量部件关联程度,能够捕捉到风机故障关联的时空特征,对部件故障关联做出准确预测。
(3) 仿真结果表明,所提策略可充分利用故障关联不确定性下各部件维护时间区间进行联合维护,减少了出海维护的次数,降低了维护成本。
参考文献
-
[1]葛畅, 阎洁, 刘永前, 等. 海上风电场运行控制维护关键技术综述[J]. 中国电机工程学报, 2022, 42(12): 4278-4292.
-
[2]万远琛, 王凯, 初岳峰. 海上风电运维的技术现状和发展综述[J]. 船舶工程, 2020, 42(12): 10-15.
-
[3]王震, 鲍春莉. 中国海洋能源发展报告2023[M]. 北京: 石油工业出版社, 2023: 10-36.
-
[4]符杨, 许伟欣, 刘璐洁. 海上风电运行维护策略研究[J]. 上海电力学院学报, 2015, 31(3): 219-222.
-
[5]THOMAS L C. A survey of maintenance and replacement models for maintainability and reliability of multi-item systems[J]. Reliability Engineering, 1986, 16(4): 297-309.
-
[6]赵洪山, 张健平, 高夺, 等. 风电机组的状态-机会维修策略[J]. 中国电机工程学报, 2015, 35(15): 3851-3858.
-
[7]符杨, 许伟欣, 刘璐洁, 等. 考虑天气因素的海上风电机组预防性机会维护策略优化方法[J]. 中国电机工程学报, 2018, 38(20): 5947-5956.
-
[8]ZHOU P, YIN P T. An opportunistic condition-based maintenance strategy for offshore wind farm based on predictive analytics[J]. Renewable and Sustainable Energy Reviews, 2019, 109: 1-9.
-
[9]PAPADOPOULOS P, COIT D W, EZZAT A A. Seizing opportunity: maintenance optimization in offshore wind farms considering accessibility, production, and crew dispatch[J]. IEEE Transactions on Sustainable Energy, 2021, 13(1): 111-121.
-
[10]LIU Q, LI Z, XIA T, et al. Integrated structural dependence and stochastic dependence for opportunistic maintenance of wind turbines by considering carbon emissions[J]. Energies, 2022, 15(2): 1-21.
-
[11]刘勤明, 王海洲, 成卉, 等. 考虑故障相关与外部冲击的风电机组机会维护策略研究[J]. 机械设计, 2022, 39(8): 48-57.
-
[12]逯红霞, 张蕊萍, 董海鹰. 考虑故障相关性的风电机组维修策略[J]. 可再生能源, 2020, 38(4): 477-483.
-
[13]符杨, 杨凡, 刘璐洁, 等. 考虑部件相关性的海上风电机组预防性维护策略[J]. 电网技术, 2019, 43(11): 4057-4063.
-
[14]宋明阳, 瞿晟珉, 秦少茜, 等. 基于故障风险水平的海上风电场机会维护策略[J]. 电力工程技术, 2023, 42(6): 117-129.
-
[15]谢鲁冰. 海上风电机组动态机会成组维修策略的研究[D]. 北京: 华北电力大学, 2021.
-
[16]黄冬梅, 陈欢, 王宁, 等. 基于自适应图注意力网络的短期用户负荷预测[J]. 电力系统保护与控制, 2023, 51(20): 140-149.
-
[17]DEY R, SALEM F M. Gate-variants of gated recurrent unit (GRU) neural networks[C]//2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS). Boston, USA: IEEE, 2017: 1597-1600.