近年来，传统能源日渐枯竭，化石燃料燃烧产生的有害气体引发全球生态问题^[1]，能源需求与环保面临双重压力。为顺应绿色低碳发展趋势，我国提出争取在2030年达到碳排放峰值，2060年前实现碳中和的“双碳”目标^[2]。2021年，中央财经委员会第九次会议强调要构建清洁低碳安全高效的能源体系，控制化石能源总量，实施可再生能源替代行动，构建以新能源为主体的新型电力系统^[3]。

要构建新型电力系统，解决空间上大范围和时间上长周期的电力电量平衡问题是关键。氢能具有能量密度大、转化效率高、零碳清洁等优势，可以作为与电能双向转化的载体，解决源侧大规模电量消纳困难和可再生能源不确定性冲击电网的问题^[4]。文献[5]提出了一种基于电制氢装置特性的风储制氢电厂效率优化控制策略。文献[6]建立了计及风电消纳的氢燃料电池模型，用电池功率的多次函数表示其发电与产热效率。文献[7]研究了电网与交通网的协同调度，建立了考虑加氢站全周期建设的电氢汽车模型。文献[8]建立了基于氢气充放流量约束和容量约束的储氢装置日间调度模型。文献[9]提出了一种基于合作博弈的含共享氢储能的微网群调度策略。文献[10]在氢能制储与运输环节间加入纯化技术，建立了考虑氢气纯度指标的氢能运输优化模型。以上研究大多侧重于氢能应用链内某一单独环节的具体问题，但实际上电网和氢网分属不同主体，疏于考虑全局信息可能影响整体规划效果。

随着能源转型过程的不断深入，储能作为电力系统调节供需平衡、保障能源安全、应对气候变化的有效措施，逐渐成为行业研究热点。文献[11]将移动储能容量作为决策变量，构建了灾后配电网经济性和恢复力均衡模型。文献[12]考虑移动储能的日常闲置情况，提出了一种综合移动储能调度和无功优化的主动配电网分层控制策略。但现有移动储能的实现大多依赖电池，充放电过程能耗较大且伴随装置老化问题。

基于以上研究，本文以高比例新能源机组接入的园区集群为研究对象，以提升集群运行经济性、提升新能源消纳水平、降低系统碳排放量为研究目标，构建了基于移动储氢的电-氢网络模型和电氢协同经济调度模型。最后，通过算例仿真分析，验证模型在促进新能源消纳、降低碳排放、协调区域电量、提高经济性和灵活性方面的积极作用。

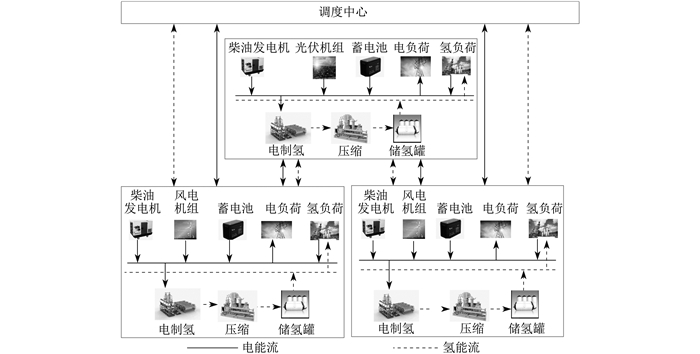
本文所提出的园区集群主要由高比例新能源机组接入的工业园区构成。引入调度中心作为园区间能量互动的协调方，优先协调集群的电能需求，使配电网最大化消纳富余发电，并补充负荷缺额。另外，结合园区能量平衡情况与成本优化结果制定氢网计划，通过氢网路径运输储氢罐至各节点进行氢能分配。园区集群框架如图 1所示。

针对新能源发电的不确定性，选择有快速启动和快速响应能力的质子交换膜电解槽完成氢气制取。绿氢被压缩储存后具有较高的能量密度，其中：一部分可直接被电场附近的燃料电池利用；其余氢气通过运氢车运输到其他园区，响应其电力负载需求。在氢气运输方面，由于氢气分子很小，在钢材料储运设备中的泄漏率约为天然气的3倍，且使用管道运氢涉及众多装置(如焊接线、阀门、泵等)，有可能增加泄漏风险^[13]，因此采用长导管拖车运氢有利于全面排查氢气的泄漏问题，同时节省大量的基建投资，可兼顾经济性和安全性。

移动储氢模型的本质是对网络节点能量状态的追踪。一些研究用0-1变量来表征单个储能装置的能量状态^[14]，但随着储能规模的扩大，计算时间增加，工程实践的优化难度有所提升。本文将电-氢网络中的节点能量建模为连续变量，通过储能容量决定能量的充放状态和功率。这种模型求解速度较快，适用于集群的日前优化及需要快速调度的应急场景。该模型同样适用于新型电力系统中富余能量的大规模存储调度。

节点电能交互模型为

$ \begin{equation*} E_{n, t}=E_{n, t-1}+E_{n, t}^{\text {in }}-E_{n, t}^{\text {out }} \end{equation*} $

(1)

式中: $E_{n, t}, E_{, t-1}-t$时段、$t-1$时段电网节点$n$中的电能；

$E_{n, t}^{\text {in }}, E_{n, t}^{\text {out }} t$时段电网节点$n$中注入和流出的电能。

$ \begin{align*} 0 \leqslant E_{n, t}^{\mathrm{in}} \leqslant \min \left\{E_{\max }^{\mathrm{WT}}, E_{\max }^{\mathrm{PV}}, E_{\max }^{\mathrm{DG}}, E_{\max }^{\mathrm{ESS}, \text { out }}, E_{\max }^{\mathrm{HFC}}\right\} \end{align*} $

(2)

$ 0 \leqslant E_{n, t}^{\text {out }} \leqslant \min \left\{E_{\max }^{\mathrm{Ioad}}, E_{\max }^{\mathrm{EL}}, E_{\max }^{\mathrm{ESS}, \text { in }}\right\} $

(3)

式中: $E_{\text {max }}^{\mathrm{wT}}, E_{\text {max }}^{\mathrm{PV}}, E_{\text {max }}^{\mathrm{DG}}$ —风电机组、光伏机组、柴油发电机的最大发电量；

$E_{\max }^{\mathrm{ESS}, \text { out }}, E_{\max }^{\mathrm{HFC}}$——蓄电池和氢燃料电池的最大发电量；

$E_{\max }^{\text {load }}, E_{\max }^{\mathrm{EL}}, E_{\max }^{\mathrm{ESS}, \text { in }}$——负荷、电解槽、蓄电池充电的最大耗电量。

电网节点电量与功率的关系模型如下：

$ E_{n, t} =P_{n, t} \Delta t $

(4)

$E_{n, t}^{\mathrm{ESS}, \text { in }} =\eta P_{n, t}^{\mathrm{ESS}, \text { in }} \Delta t $

(5)

$ E_{n, t}^{\mathrm{ESS}, \text { out }} =\frac{P_{n, t}^{\mathrm{ESS}, \text { out }}}{\eta} \Delta t $

(6)

式中: $P_{n, t}-t$时段电网节点$n$中机组的功率；

$\Delta t$——单位调度时段；

$P_{n, t}^{\mathrm{ESS}, \text { in }}, P_{n, t}^{\mathrm{ESS}, \text { out }}-t$时段电网节点$n$中蓄电池充电功率、放电功率；

$\eta$——蓄电池充放电效率。

将单位调度时段设置为1 h，此时电量与节点功率在数值上可视为等值。蓄电池的充放电功率约束和状态约束条件分别为

$ 0 \leqslant P_{n, t}^{\mathrm{ESS}, \text { in }} \leqslant \min \left\{E_{n, t}, \alpha_{n, t} E_{\max }^{\mathrm{ESS}, \text { in }}\right\} $

(7)

$ 0 \leqslant P_{n, t}^{\mathrm{ESS} \text { out }} \leqslant \min \left\{E_{n, t}, \beta_{n, t} E_{\max }^{\mathrm{ESS}, \text { out }}\right\} $

(8)

$ \alpha_{n, t}+\beta_{n, t} \leqslant 1 $

(9)

式中: $\alpha_{n, t}, \beta_{n, t}$ —蓄电池的充电指示、放电指示, 为$0-1$变量。

由于源荷两侧存在物理距离，因此氢能调度主要通过车辆在氢网节点的氢站内装卸储氢罐来实现。节点氢能交互模型为

$ S_{n, t}=S_{n, t-1}+S_{n, t}^{\text {in }}-S_{n, t}^{\text {out }} $

(10)

$ 0 \leqslant S_{n, t}^{\text {out }} \leqslant S_{n, t} \leqslant S_{n, t}^{\text {in }} \leqslant S_{n}^{\max } $

(11)

式中: $S_{n, t}, S_{n, t-1}-t$时段和$t-1$时段氢网节点$n$中存储的氢量；

$S_{n, t}^{\text {in }}, S_{n, t}^{\text {out } } ——t$时段氢网节点$n$中注入和流出的氢量；

$S_{n}^{\max }$——氢网节点$n$的最大储氢量，数值为常数。

其中，有关氢气制用的电解槽和氢燃料电池的模型分别为

$ S_{\mathrm{EL}, t} =\eta_{\mathrm{EL}} \tau_{1} P_{\mathrm{EL}, t} \Delta t $

(12)

$ P_{\mathrm{HFC}, t} =\frac{\eta_{\mathrm{HFC}} \tau_{2} S_{\mathrm{HFC}, t}}{\Delta t} $

(13)

式中：$S_{\mathrm{EL}, t}—— t$时段由电解槽转换的氢气量；

$\eta_{\mathrm{EL}}, \eta_{\mathrm{HFC}}$——电解槽和氢燃料电池的工作效率；

$\tau_{1}$——每kWh电能电解产生的氢气量；

$P_{\mathrm{EL}, t} — t$时段电解槽的耗电功率；

$P_{\mathrm{HFC}, t}-t$时段氢燃料电池的发电功率；

$\tau_{2}$ —每kg氢气燃烧产生的电能；

$S_{\mathrm{HFC}, t}$ — $t$时段氢燃料电池的耗电量。

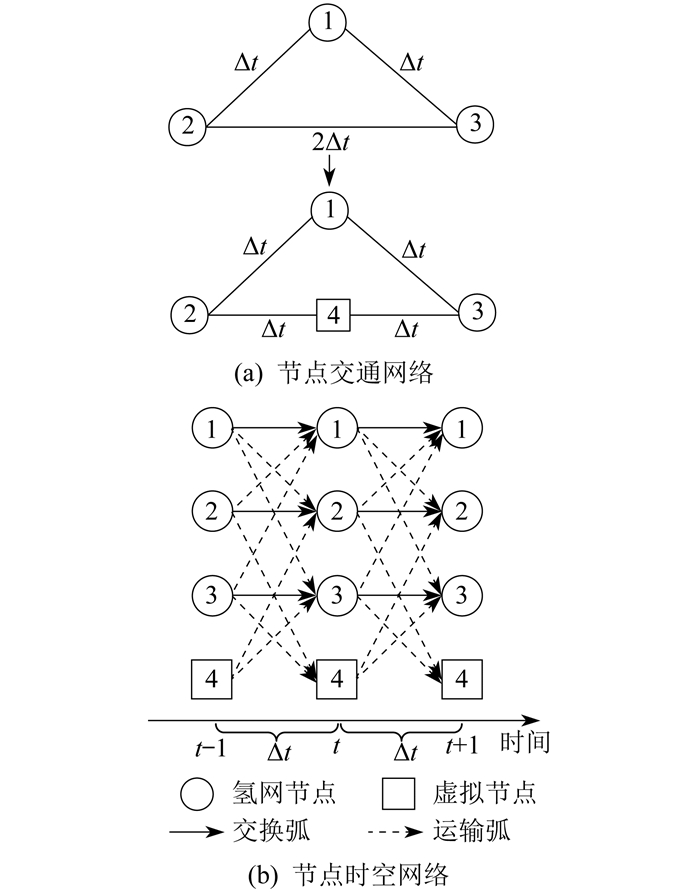
移动储氢单元是电-氢网络耦合的关键环节，本文采用时空网络建立运氢车的路径模型^[15]。图 2为氢网节点交通网络和时空网络模型。其中，假设车辆在图 2(a)中1—2、1—3、2—3之间的行驶时间近似为Δt、Δt、2Δt。加入虚拟节点4，以保证车辆在节点间的移动时间大致相等；图 2(b)中虚线表示节点间的行车路径，实线表示车辆停留在某一节点内。虚拟节点只作为真实氢网节点间的中转，不允许任何车辆停留。

在时空网络中，运氢车的位移约束条件为

$ \sum\limits_{m n \in A} I_{k, m n}^{t}=1 $

(14)

$ \sum\limits_{m n \in A_{m}^{+}} I_{k, m n}^{t+1}-\sum\limits_{m n \in A_{m}^{-}} I_{k, m n}^{t}=0 $

(15)

$\sum\limits_{m n \in A_{m}^{*}} I_{k, m n}^{1}-I_{k, m}^{0}=0 $

(16)

$\sum\limits_{m n \in A_{m}^{*}} I_{k, m n}^{N_{t}}-I_{k, m}^{N_{k}}=0 $

(17)

式中: $m n$ —从节点$m$到节点$n$的网络弧；

$A$——时空网络中弧的集合；

$I_{k, m n}^{t}$ —运氢车$k$在$t$时段中与弧的连接状态，为$0-1$变量；

$A_{m}^{+}, A_{m}^{-}$—以节点$m$为起点和终点的时空网络弧的集合；

$I_{k, m}^{0}, I_{k, m n}^{N_{1}}$——运输车$k$的初始状态和最终状态变量，均为$0-1$变量；

$N_{t}$——时段数。

式(14)表示车辆$k$在$t$时段中只能处于一个运行状态。式(15)表示在相邻时刻，各氢网节点内车辆的位移状态连续。式(16)表示在初始调度时段1，节点车辆驶出数量等于车辆$k$的初始状态。式(17)表示最后调度时段$N_{t}$，节点车辆驶入数量等于车辆$k$的最终状态。

电氢协同经济调度模型以系统运维成本$C_{\mathrm{op}, t}$、能量运输成本$C_{\text {trans }, t}$、弃风弃光惩罚成本C_ren，t、碳排放成本C_CO2，t 之和最小作为优化目标，公式为

$ \begin{equation*} \min C_{\text {total }}=\sum\limits_{t=1}^{N_{t}}\left(C_{\mathrm{op}, t}+C_{\text {trans }, t}+C_{\text {ren }, t}+C_{\mathrm{CO}_{2}, t}\right) \end{equation*} $

(18)

式中：$C_{\text {total }}$ —系统总运行成本。

系统运维成本公式为

$ \begin{equation*} C_{\mathrm{op}, t}=C_{\mathrm{op}, t}^{\mathrm{pV}}+C_{\mathrm{op}, t}^{\mathrm{wT}}+C_{\mathrm{op}, t}^{\mathrm{DG}}+C_{\mathrm{op}, t}^{\mathrm{ESS}}+C_{\mathrm{op}, t}^{\mathrm{EL}}+C_{\mathrm{op}, t}^{\mathrm{HFC}}+C_{\mathrm{op}, t}^{\mathrm{HS}} \end{equation*} $

(19)

$C_{\mathrm{op}, t}^{\mathrm{PV}}=\sum\limits_{n=1}^N U_{\mathrm{op}}^{\mathrm{PV}} P_{n, t}^{\mathrm{PV}} $

(20)

$C_{\mathrm{op}, t}^{\mathrm{WT}}=\sum\limits_{n=1}^N U_{\mathrm{op}}^{\mathrm{WT}} P_{n, t}^{\mathrm{wT}} $

(21)

$ C_{\mathrm{op}, t}^{\mathrm{DG}}=\sum\limits_{n=1}^N U_{\mathrm{op}}^{\mathrm{DG}} P_{n, t}^{\mathrm{DG}} $

(22)

$ \begin{equation*} C_{\mathrm{op}, t}^{\mathrm{ESS}}=\sum\limits_{n=1}^{N} \varepsilon_{\mathrm{ESS}}\left(P_{n, t}^{\mathrm{ESS}, \text { in }}+P_{n, t}^{\mathrm{ESS}, \text { out }}\right) \end{equation*} $

(23)

$ C_{\mathrm{op}, t}^{\mathrm{EL}} =\sum\limits_{n=1}^{N} U_{\mathrm{op}}^{\mathrm{EL}} P_{n, t}^{\mathrm{EL}} $

(24)

$ C_{\mathrm{op}, t}^{\mathrm{HFC}} =\sum\limits_{n=1}^{N} U_{\mathrm{op}}^{\mathrm{HFC}} P_{n, t}^{\mathrm{HFC}} $

(25)

$\begin{equation*} C_{\mathrm{op}, t}^{\mathrm{HS}}=\sum\limits_{n=1}^{N} \rho_{\mathrm{H}_{2}}\left(P_{n, t}^{\mathrm{HS}, \text { in }}+P_{n, t}^{\mathrm{HS}, \text { out }}\right) \end{equation*} $

(26)

式中：$C_{\mathrm{op}, t}^{i}$ —各类装置的运维成本，$i=\mathrm{PV}, \mathrm{WT}, \mathrm{DG}$, ESS，EL，HFC，HS，分别表示光伏机组、风电机组、柴油发电机、蓄电池、电解槽、氢燃料电池、储氢罐；

$N$——氢网节点数量；

$U_{\mathrm{op}}^{i}$ —各类装置的单位功率运维成本；

$P_{n, t}^{i} — t$时段氢网节点$n$上各类装置的功率；

$\varepsilon_{\mathrm{ESS}}$——蓄电池充放电的单位功率维护成本；

$\rho_{\mathrm{H}_{2}}$ —储氢罐单位功率维护成本；

$P_{n, t}^{\mathrm{HS}, \text { in }}, P_{n, t}^{\mathrm{HS}, \text { out }} —t$时段氢网节点$n$储氢罐的充电功率和放电功率。

输送通道是上层能量网络中的一部分，输送电能和氢能必须缴纳能量传输费用。能量传输成本公式为

$ \begin{equation*} C_{\text {trans }, t}=\sum\limits_{l=1}^{L} \gamma_{\mathrm{E}} P_{l, t}^{\mathrm{E} 2 \mathrm{E}}+\sum\limits_{m n}^{A} c_{\mathrm{H}} I_{k, m n}^{t} \end{equation*} $

(27)

式中：$L$——电-氢网络节点间的联络线数量；

$\gamma_{\mathrm{E}}$——单位功率电能的过网折算费用；

$P_{l, t}^{\mathrm{E} 2 \mathrm{E}}-t$时段电网联络线$l$上的传输功率；

$c_{\mathrm{H}}$——氢网节点间的单次运氢成本。

弃风弃光惩罚成本公式为

$ \begin{equation*} C_{\mathrm{ren}, t}=\sum\limits_{n=1}^{N}\left(1-\delta_{t}\right) K_{\mathrm{ren}} P_{n, t}^{\mathrm{ren}} \end{equation*} $

(28)

式中: $\delta_{t}-t$时段新能源利用率；

$K_{\mathrm{ren}}$ —单位功率下的弃风弃光惩罚系数；

$P_{n, t}^{\mathrm{ren}} — t$时段电网节点$n$的新能源输出功率。

碳排放成本公式为

$ \begin{equation*} C_{\mathrm{CO}_{2}, t}=\sum\limits_{n=1}^{N} a P_{n, t}^{\mathrm{DG}} \varLambda_{\mathrm{CO}_{2}} \end{equation*} $

(29)

式中：$a$ —柴油发电机的碳排放量系数；

$\varLambda_{\mathrm{CO}_{2}}$ —单位碳排放量惩罚系数。

储氢罐约束条件为

$0 \leqslant H_{j, \text { HS }}^{t} \leqslant H_{j, \text { HS }}^{N}, \forall j \in \varOmega_{\mathrm{HS}} $

(30)

$ H_{j, \text { HS }}^{t+1}=H_{j, \text { HS }}^{t}+H_{j, \text { in, HS }}^{t}-H_{j, \text { out, HS }}^{t} $

(31)

$H_{j, \text { HS }}^{1}=\omega H_{j, \text { HS }}^{N} $

(32)

$ 0 \leqslant H_{j, \text { in, HS }}^{t} \leqslant \mu_{j, \text { in } \text { HS }}^{t} H_{j, \text { in HS }}^{N} $

(33)

$ 0 \leqslant H_{j, \text { out, HS }}^{t} \leqslant \mu_{j, \text { out, HS }}^{t} H_{j, \text { out, HS }}^{N} $

(34)

$ \mu_{j, \text { in }, \mathrm{HS}}^{t}+\mu_{j, \text { out, HS }}^{t} \leqslant 1 $

(35)

式中: $H_{j, \mathrm{HS}}^{t}, H_{j, \text { in, HS }}^{t}, H_{j, \text { out }, \mathrm{HS}}^{t} —— t$时段储氢罐中的氢量、流入量、流出量；

$H_{j, \mathrm{HS}}^{\mathrm{N}}$——储氢罐的额定容量；

$\varOmega_{\mathrm{HS}}$——储氢罐集合；

$\omega$——储氢罐个数；

$\mu_{j, \text { in, HS }}^{t}, \mu_{j, \text { out HS }}^{t}$ —氢气充、放指示, $0-1$变量。

上述公式中：式(30)为储氢量约束；式(31)为储氢平衡约束；式(32)为初始时段储氢量的不变约束；式(33)和式(34)为单位时段氢气流量约束；式(35)为氢气状态约束。

电能平衡约束与氢能平衡约束条件分别为

$ \sum\limits_{n=1}^{N} E_{n, t}^{\text {out }}=\sum\limits_{n=1}^{N} E_{n, t}^{\text {in }} $

(36)

$ \sum\limits_{n=1}^{N} S_{n, t}^{\text {out }}=\sum\limits_{n=1}^{N} S_{n, t}^{\text {in }} $

(37)

潮流约束条件为

$ \begin{align*} & \boldsymbol{\varPi}_{\mathrm{np}} P_{t}^{\mathrm{pV}}+\boldsymbol{\varPi}_{\mathrm{nw}} P_{t}^{\mathrm{wT}}+\boldsymbol{\varPi}_{\mathrm{nh}} P_{t}^{\mathrm{HFC}}+\boldsymbol{\varPi}_{\mathrm{ne}} P_{t}^{\mathrm{ESS}}+\boldsymbol{\varPi}_{\mathrm{ng}} P_{t}^{\mathrm{DG}}- \\ & \quad \boldsymbol{\varPi}_{\mathrm{nd}} P_{t}^{\mathrm{Poad}}=\boldsymbol{\varPi}_{\mathrm{nl}} P_{t}^{{\rm{l}}} \end{align*} $

(38)

式中：$\boldsymbol{\varPi}_{\mathrm{np}}$ —电网节点与光伏机组的关联矩阵；

$P_{t}^{\mathrm{PV}}, P_{t}^{\mathrm{WT}}, P_{t}^{\mathrm{HFC}}, P_{t}^{\mathrm{ESS}}, P_{t}^{\mathrm{DG}} $ —时段光伏机组、风电机组、氢燃料电池、蓄电池、柴油发电机的功率；

$\boldsymbol{\varPi}_{\mathrm{nw}}$——电网节点与风电机组的关联矩阵；

$\boldsymbol{\varPi}_{\mathrm{nh}}$——电网节点与氢燃料电池的关联矩阵；

$\boldsymbol{\varPi}_{\mathrm{ne}}$——电网节点与蓄电池的关联矩阵；

$\boldsymbol{\varPi}_{\mathrm{ng}}$——电网节点与柴油发电机的关联矩阵；

$\boldsymbol{\varPi}_{\mathrm{nd}}$——电网节点与负荷节点的关联矩阵；

$P_{t}^{\text {load } } —t$时段的负荷；

$\boldsymbol{\varPi}_{\mathrm{n} 1}$ —电网节点与线路的关联矩阵；

$P_{t}^{\mathrm{l}}$ — $t$时段的线路功率。

本文在改进的IEEE 30节点系统^[16]上设置3种场景进行仿真和分析，以验证模型的有效性。算例选择使用MATLAB R2018a在YALMIP优化工具箱中实现，并用CPLEX求解器进行求解。

采用IEEE 30节点电网与4节点氢网的耦合网络进行仿真。部分仿真数据参照文献[15-16]。具体仿真场景设置如下：场景1，高比例新能源接入的园区常规电网经济调度；场景2，在场景1中加入包括电解槽、储氢罐和氢燃料电池在内的氢能应用链；场景3，构建氢网，在场景2的基础上加入移动储氢单元。氢网节点间车辆的移动时长相等，场景2和场景3的储氢罐初始状态均设置为最大容量的50%。

IEEE 30节点系统在不同场景下总运行成本、弃风弃光量、弃风弃光率及碳排放量如表 1所示。

由表 1可以看出，从场景1到场景3各项指标都呈现递减趋势。总运行成本方面，与常规调度相比，固定储氢参与调度后降低了21.3%，移动储氢则降低了38.3%；弃风弃光率方面，固定储氢参与后下降了12.2%，移动储氢参与后下降了26.8%；碳排放量方面，固定储氢参与后减少了37.8%，移动储氢参与后减少了86.6%。由此可得，氢能可以有效降低系统运行成本，提高新能源消纳率，降低碳排放量。特别是移动储氢单元的减碳效果显著，符合绿色可持续发展的理念。

部分详细成本如表 2所示。其中，机组运行成本是新能源机组的运行成本，储能运行成本是蓄电池和氢储能装置的运行成本。

由表 2可知，与场景1相比，场景2的弃风弃光惩罚成本下降了12%，氢燃料电池功率输出也间接降低了碳排放成本。对比场景2中的固定储氢模式，场景3的机组运行成本增加了8.24%，碳排放成本降低了78.5%，弃风弃光惩罚成本降低了77.8%。移动储氢单元增加了氢气用量，进一步提升了风光消纳水平。负荷得到氢网支持后，碳排放量进一步降低。因此，移动储氢虽然增加了机组运行成本，但对于整个集群而言仍具有经济价值，而且提升了环境友好性，验证了模型的有效性。

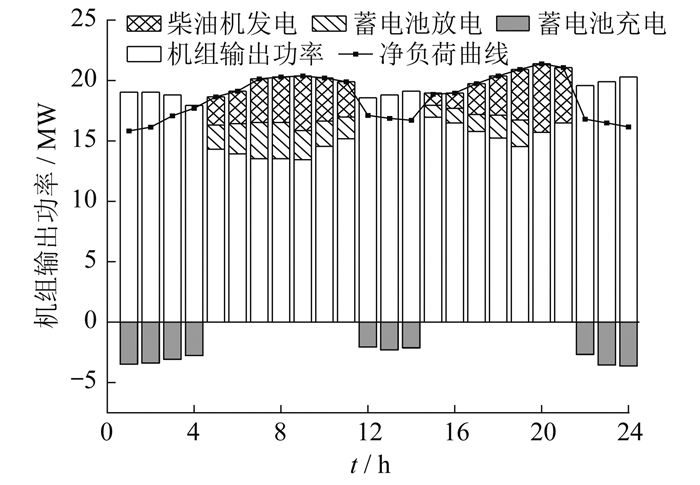
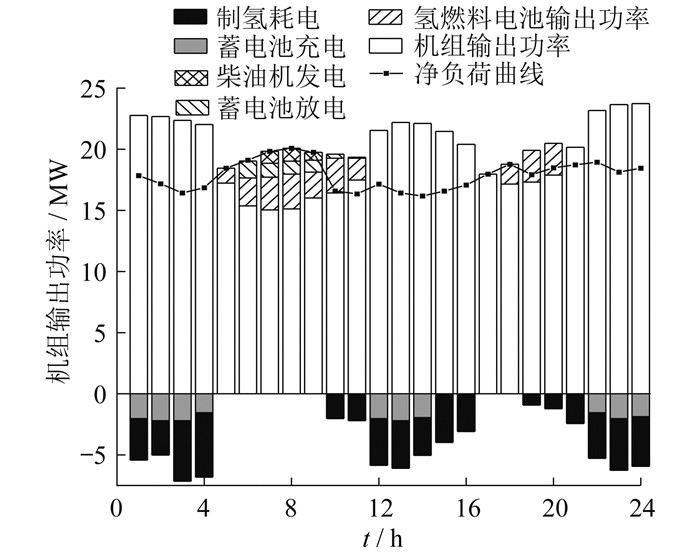
场景1和场景2的机组输出功率与储能优化结果分别如图 3和图 4所示。场景1中仅靠电网完成调度，由于蓄电池存在容量限制，主要由柴油发电机补足负荷缺额，这会导致机组高发时能源出现冗余，负荷高峰时碳排放量增大。场景2中加入了固定氢储能，与场景1相比储能容量增大，减少了弃风弃光量。负荷高峰时有氢能支撑，柴油发电机输出功率明显减少。但由于没有形成氢网，风光机组输出功率的高峰不同，面对缺额仍需要柴油发电机发电，净负荷曲线变化不大。由上可得，固定储氢主要作用于各园区内部，集群的整体调度仍有待进一步优化。

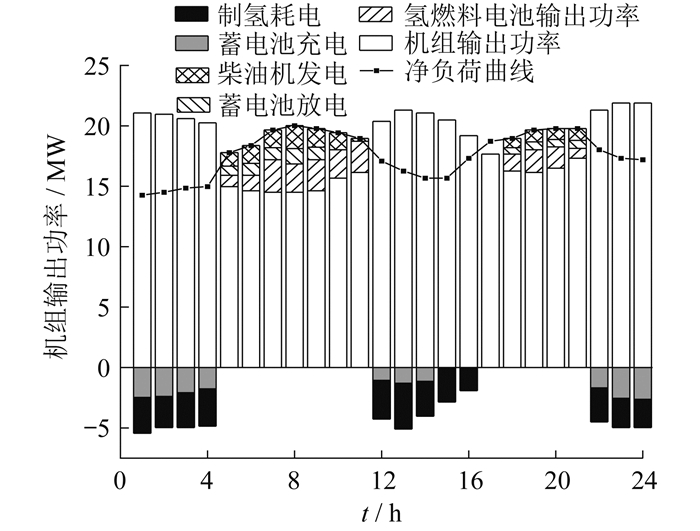
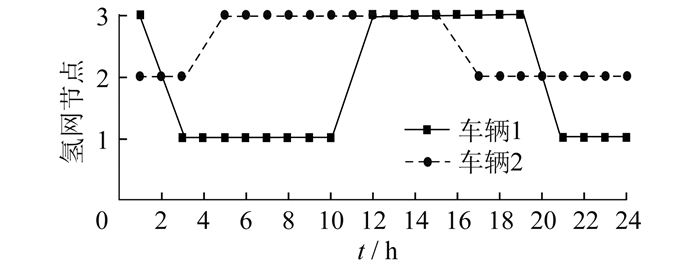
场景3的机组输出功率与储能优化结果如图 5所示。车辆移动路径如图 6所示。

氢网节点1和节点2在风电场附近，节点3在光伏电站附近。调度初始，车辆1和车辆2分别位于氢网节点3和节点2。晚间光伏机组输出功率为零，风机高发。01：00时，调用节点3的空载氢罐至节点1。03：00时，车辆1到达节点1，此时氢网加入调度，制氢耗电明显增加；车辆2将部分满载氢罐运往节点3，补充光伏电厂负荷缺额。05：00—9：00，集群机组出力减少，负荷需求爬升，而满载氢罐于05：00到达节点3，电网各负荷节点都有氢能支撑，氢燃料电池补足缺额。10：00时，光伏电厂进入高发期，由于移动储氢的参与，氢气的制取与利用可以异时异地进行，故10：00— 11：00光伏电厂仍能电解制氢，机组输出功率也因新能源消纳水平的提升而增加。经上述调度后，氢网能量足以支撑后续负荷缺额，18：00— 20：00缺额全部由氢燃料电池补足。18：00后风电高发，车辆2装载部分空载氢罐返回节点2；20：00时，氢能彻底完成支撑任务，车辆1将剩余空氢罐由节点3运至节点1，参与风电消纳工作。至24：00，全天的电氢协同调度任务完成。

综上所述，与常规电网优化相比，电氢协同调度模式能有效提升新能源消纳水平，降低碳排放。与固定储氢相比，移动储氢参与调度后净负荷曲线更加平滑，有效缓解了调峰机组压力，解决了能源冗余，提高了集群运行的灵活性，由此证明了本文提出的基于移动储氢的电氢协同调度模型的可行性和有效性。

本文以高比例新能源机组接入的园区集群为研究对象，构建了基于移动储氢的电-氢网络模型，并在此基础上提出了一种基于移动储氢的电氢耦合协同调度模型。经仿真分析后得出以下结论。

(1) 通过在园区中建立氢网，利用移动储氢实现电-氢网络的互联互通，可以均衡集群能量分布，提升集群的消纳水平，减少碳排放量。

(2) 面对同样的调度需求，固定储能往往需要设置多处储能站点，移动储能以更少的建设成本满足不断变化的电网条件，减少了储能资产的闲置，提高了集群的经济效益和运行灵活性。